探討綜合法和分析法在初中幾何解題中的應用
戴燕紅

摘 要:初中幾何解題是初中學習的重要內容,掌握必要的幾何解題方法非常重要.本文就綜合法與分析法在初中幾何中的應用進行探討.綜合法與分析法并不是孤立存在的,在初中幾何試題求證過程中,兩種方法的運用是密不可分的,學生通過分析法對幾何試題進行分析,運用綜合法對試題進行羅列求證,最終完成幾何試題的求證.
關鍵詞:綜合法;解析法;初中幾何解題
中圖分類號:G632? ? ? 文獻標識碼:A? ? ? 文章編號:1008-0333(2020)23-0007-02
幾何解題需要清醒的頭腦與沉穩的心情,不要一看到幾何證明題目憑著自己的直覺就開始著手解題,首先需要運用分析法細致、全面地分析幾何題目的解題思路,然后再運用綜合法對幾何題目整體把控,開始證明.分析法講的是以所要證明的幾何題目結論為出發點,向前一步步尋找使其成立的充分條件,直到找到一個符合題目的條件.
綜合法講的是在幾何題目證明當中,通過已知條件開始證明,解題過程環環相扣,最終得到幾何題目所要證明的結論成立,簡而言之就是通過已知去看可知,步步接近未知的證明方法.綜合法是初中幾何試題常用的解題方法.
一、綜合法和分析法在初中幾何解題中的應用
例1
如圖1所示,三角形ABC是一個等腰直角三角形,CF是直角∠ACB的角平分線,BF是外角∠ABE的角平分線,CF與BF這兩條角平分線相交于點F,探求∠BFC與∠BAC之間的數量關系.
解 根據已知條件,∠ACB=90°,CF是∠ACB的角平分線,所以∠CAB=∠BCF=1/2∠BCA=45°.因為BF是外角∠ABE的角平分線,所以∠ABF=1/2∠EBA=1/2(180°-∠CBA)=1/2(180°-45°)=67.5°.所以∠FBC=67.5°+45°=112.5°,所以∠BFC=180°-∠FBC-∠BCF=180°-112.5°-45=22.5°.又因為∠CAB=45°,所以∠BFC=1/2∠BAC.
例2
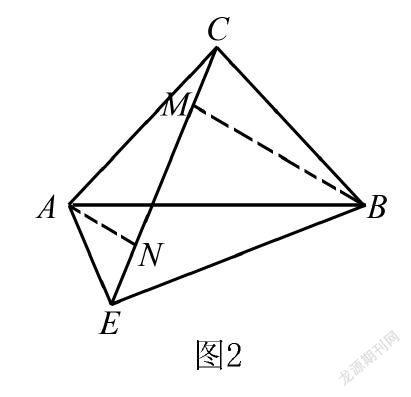
如圖2所示,在等腰Rt△ABC中,∠ACB=90°,點E是△ABC之外的一點,并且∠AEC=45°,求證線段AE ⊥BE.
首先運用分析法探索幾何題目的解題路線:若證明線段AE⊥BE,已知∠AEC=45°,需要證明∠BEC=45°.分析到這里,解題遇到第一個瓶頸,沒有更多的已知條件可用,我們需要考慮借助輔助線來增加已知條件,通常會首先考慮具有特殊性的45°角.繼續分析:作線段BM⊥EC并相交于點M,須證明線段BM=EM,線段BM處在△BMC當中,通過看圖直覺發現并沒有與其全等的三角形,因此還需要增加一條輔助線構建一個與三角形BMC全等的三角形.已知AC=BC,作線段AN ⊥EC相交于點N,得出AN=EN,進而可以運用角角邊的全等三角形定理證明△CBM 全等于△ACN,進一步得到線段BM=CN.因為線段CM=AE=EN,所以線段CN=EM,所以線段BM=EM,所以∠BEC=45°.進而得出所需要求證的結論,線段AE⊥BE.
二、激發學生幾何學習興趣,促進綜合法和分析法在初中幾何解題中的應用
興趣是最好的老師,學生自身對幾何學習產生興趣直接促進綜合法和分析法在初中幾何解題中的應用.
首先,教師可以舉出幾何學習中具有代表性、通俗易懂的背景材料.舉例來講,教師在傳授學生“平行線”這一概念的時候,教師可以先讓學生們觀察鐵軌的圖片、長方形黑板的左右邊緣、直尺的上下邊緣等,引導學生發現以上例子具有哪些共同點.學生在觀察、分辨之后,老師可以讓學生舉手發言,同時通過舉手數量來初步衡量學生們的觀察情況,然后教師順理成章地將本節課“平行線”的概念引出來,學生們就更容易理解“平行線”這一抽象的概念了.
其次,可以通過就具體的實驗來調動學生學習幾何的積極性,恰到好處地使用幾何教學工具就顯得尤為重要,老師指導學生自己動手開展幾何實驗,引導學生主動探索幾何的奧秘,由此一來,不僅在幾何情景課堂創設方面收獲意想不到的良好效果,同時還有助于培養初中學生的學習能力.比如,在學習證明三角形全等、角與角之間的關系時,教師可以向學生們發出疑問,兩個三角形三個角的度數都一樣就是全等三角形嗎?學生們幾乎都回答是,然后老師拿出兩個角度相同但邊長不等的兩個三角形卡片,讓學生們動手將兩個三角形重合,學生們在親自動手實踐之后發現,兩個三角形卡片大小不一致,根本不能說是全等三角形.學生們會繼續思考,具備怎樣的條件才能是全等三角形?進而對初中幾何的學習興趣愈加濃厚.
在初中數學學習當中,幾何部分的學習對于初中生來講非常重要,也是很多學生認為較難的學習內容,很多幾何圖形較為抽象,需要學生在腦海中建立立體模型,所以,在初中幾何學習中,教師要逐步降低幾何題目的解題難度,對學生看到幾何題目后的解題思路與尋找解題路徑能力方面進行強化,可以借助圖形、添加輔助線等來找到解題思路,幫助學生正確運用綜合法和分析法,幫助學生很快解決幾何試題的求證,提高學生幾何解題能力.加強師生之間的溝通與交流,重點監督學生幾何試題解題思路能力的掌握程度以及幾何圖形繪圖能力.在學生掌握基礎知識的同時,重點指導學生綜合法和解析法在初中幾何解題中的應用情況.
參考文獻:
[1]查書平.淺析綜合法和解析法在初中幾何解題中的應用[J].數學學習與研究,2019(15):142.
[2]黃德誠.淺談“雙垂直模型中的射影定理”在初中幾何解題中的應用[J].科學咨詢(教育科研),2018(11):85.
[3]畢明東.基于解題能力培養的初中幾何教學探析[J].成才之路,2018(03):61.
[責任編輯:李 璟]

