雙弱感知能力機器人在線協作街道搜索算法*

魏 琦，林韋達，吳 彤，任永功

遼寧師范大學計算機與信息技術學院，遼寧大連 116081

1 引言

未知區域中的目標搜索是計算幾何學和機器人學中的熱點研究問題[1-3]，在機器人搜索、探索和監控等領域有著廣泛的應用[4-5]。近年來，國內外眾多學者針對相關問題展開研究，并取得了一定成果。

本研究將機器人搜索區域抽象為街道模型[6]，即具有LR（left chain and right chain）可視性的簡單多邊形。Klein[6]最先提出街道模型，并提出機器人從街道起點s出發，在線搜索街道終點t的街道搜索問題。該模型可視作對街道、河道、賽道場景的抽象，機器人從起點出發，在線搜索并到達終點，可看到場景內的所有區域，進而完成勘察、搜索、探索等任務。針對街道搜索問題，Klein[6]給出了競爭比為5.72的在線算法，并證明算法的競爭比下界為。自此，街道模型的相關問題獲得了學術界的廣泛關注。Tseng等[7]提出了在簡單多邊形邊界上尋找所有可能作為起點和終點構成街道的點對的算法。Ghosh和Saluja[8]提出了搜索路徑轉折次數最少的街道搜索算法。針對Klein[6]提出的競爭比為5.72的街道搜索算法，多位學者先后提出新的算法，降低競爭比，提升算法效率。最終，由Icking等[9]給出了與競爭比下界相匹配的最優算法。

上述街道模型的研究中，使用的機器人都具有較強的感知能力，其攜帶的感應器不僅可以觀察可視區域內的場景，還可以測量距離和角度，使得機器人在行進的過程中可以根據感應器收集到的信息繪制出街道的局部地圖。與感知能力較強的感應器相對應的，一些研究人員將關注點放在簡單感應器上，因為其具有很多優點，如價格低廉、抗干擾能力強、適應性強等。Tovar等[10]最先提出弱感知模型，機器人攜帶的感應器僅能探測可視區域內搜索區域邊界的不連續情況，借助數據結構GNT（gap navigation tree），這些搜索區域邊界的不連續情況可被保存和更新，用于制定機器人的搜索策略。Lopez-Padilla等[11]在弱感知模型下研究了使用盤式機器人在簡單多邊形區域中搜索目標點的問題。Tabatabaei等[12]在弱感知模型下研究了街道搜索問題，受雙倍策略[13]啟發，提出了競爭比為11的在線搜索算法。Wei等[14]又針對此問題提出了競爭比為9的算法，并通過給出相匹配的競爭比下界證明了算法的最優性，同時還去掉了機器人需要攜帶位置標記裝置及使用數據結構SGNT（street gap navigation tree）的限制。

與單機器人在未知環境下搜索目標相比，使用多機器人協作完成目標搜索具有并行處理、容錯率高、信息冗余等優點[15-17]，不僅有助于克服傳感器和環境的不確定性，而且還擴展了單個機器人的搜索功能。Czyzowicz等[18]研究了使用多個機器人在一條直線上搜索目標的問題，并給出了競爭比為2的在線搜索算法。Burgard等[19]、Ortolf等[20]研究了使用多個機器人探索未知區域的問題。

在上述研究基礎上，本研究提出雙弱感知能力機器人在線協作街道搜索問題，研究使用兩個弱感知能力機器人從街道起點s出發，在預先不知道街道幾何信息的前提下，協作搜索街道終點t。本研究提出了競爭比為3的在線協作搜索算法，并通過給出相匹配的競爭比下界，證明了算法的最優性。

2 模型描述

本章將從搜索場景、感應器、機器人動作初始設定等方面給出雙弱感知能力機器人在線協作街道搜索模型的描述。

設P為一簡單多邊形，bd為P的邊界。設p、q為P內部的兩點，如果線段完全在P的內部，則稱p、q兩點相互可視。對于P內部的兩個點集A、B，若A中任意一點p，B中都至少存在一點q與之相互可視，反之亦然，則稱集合A與B相互弱可視。

定義1（街道）設P為一簡單多邊形，其邊界上有兩個不相同的點s和t。設L和R分別表示P上從s到t的兩條邊界鏈。如果L和R相互弱可視，則稱(P,s,t)為街道，其中s為起點，t為終點。

設點集Vis(a)={q∈P|a與q相互可視}表示點a(a∈P)在P內的可視區域。如圖1所示，為一街道P及其起點s的可視區域Vis(s)。兩個機器人從起點s出發，協作搜索并到達終點t，本研究的目標即為兩個機器人規劃高效的協作搜索路徑。

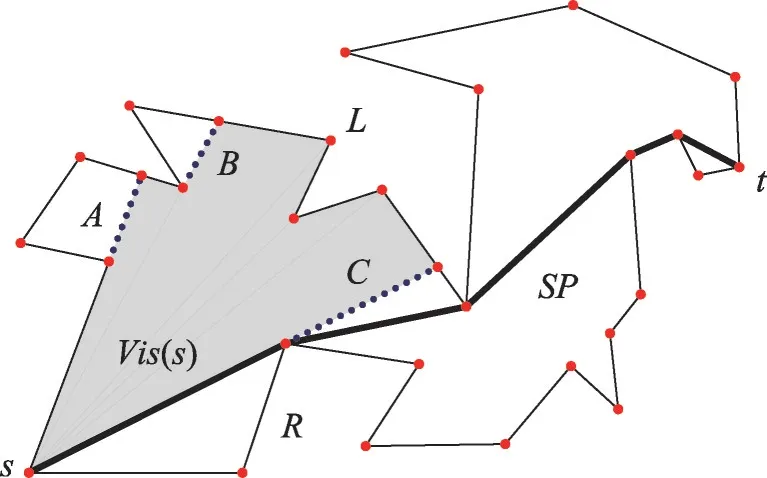
Fig.1 Street P,visibility region of P at s,gaps A,B and C,the shortest path SP圖1 街道P，Vis(s)，間隔A、B、C，最短路徑SP

定義2（間隔）設Vis(a)為機器人在街道P內a點的可視區域，Vis(a)邊界上的構造部分（非P的邊界）稱為間隔。

機器人攜帶有視覺感應器，但感知能力較弱，僅能探測可視區域內街道邊界的不連續情況（間隔），并可為間隔加上L或R標簽。相對于機器人當前所處的位置，每個間隔背后都關聯著一個不可視區域，如果不可視區域在其關聯間隔的左側，則為該間隔加上L標簽并稱之為L間隔，R間隔可按類似的方式定義。如圖1所示，機器人在起點s可探測到L間隔A、B，R間隔C。需要指出的是，終點t可能在任意一個間隔背后的不可視區域內。

在搜索過程中，隨著機器人的移動，其可視區域內的間隔會動態地發生變化。這些變化可歸因于四類事件的發生，分別是消失、分裂、合并、共線。如圖2所示，當機器人從s點走到a點時，間隔A分裂成D、E和F，間隔C消失；當機器人從a點走到b點時，間隔D消失，間隔E和F合并為H，間隔I和J共線。

Fig.2 Dynamical changes of gaps when robot moves圖2 機器人移動過程中間隔的動態變化

當可視區域內間隔發生變化時，可能會有新的間隔出現，機器人可將新出現的間隔劃分為原生間隔和非原生間隔兩類。一個間隔，如果其背后的不可視區域對機器人曾經是可視的（如圖2（c）中的間隔K），則稱之為非原生間隔；否則，稱之為原生間隔。在本研究中，機器人是不關心非原生間隔的，因為終點t不可能在其中。

機器人在街道中被抽象成一點，并設定其在搜索過程中勻速前進，其攜帶的感應器可按順時針序報告可視區域內發現的間隔，并為間隔加上L或R標簽。機器人可朝向間隔移動任意個單位步長的距離，這里的單位步長是一個較小的常量。機器人在移動的過程中，不能測量與間隔之間的距離和角度，也不能測量間隔的尺寸，只能根據可視區域內間隔的變化情況規劃搜索路徑。搜索過程中，機器人可與其他機器人實時通信，并可以識別終點t。

本研究關注使用兩個相同機器人從街道起點s出發，在預先不知道街道幾何信息的前提下，協作搜索街道終點t的算法。算法的效率使用競爭比[21]來衡量，如下列公式所示：

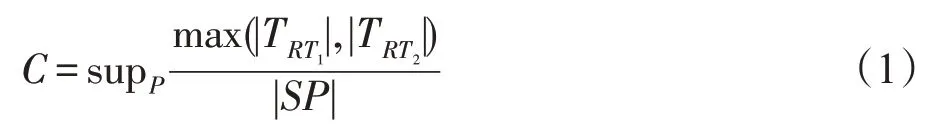
其中，C表示競爭比，P表示被搜索街道，supP表示P的所有可能情況構成集合的上確界，和分別表示機器人RT1和RT2從起點s到終點t所走的路徑，SP表示從起點s到終點t的最短路徑。

3 幾何特性

本章將分析弱感知能力機器人街道搜索過程中的幾何特性，為下章算法的提出提供依據。

每個間隔都有一個與之關聯的凹頂點，這里凹頂點是指內角和大于180°的P的頂點。如果間隔是L間隔，則其關聯凹頂點稱為L關聯凹頂點，記作vl；R關聯凹頂點可按類似的方式定義，記作vr。

定義3（極限間隔）可視區域內所有L間隔中，順時針序最后一個稱為極限L間隔，記作Glm，其關聯凹頂點記作vlm；可視區域內所有R間隔中，順時針序第一個稱為極限R間隔，記作Grm，其關聯凹頂點記作vrm（如圖3（a）所示）。

引理1機器人搜索街道的過程中，如果終點t不在其可視區域內，那么一定在極限L間隔或極限R間隔的背后。

證明假設相反情況，街道的終點t不在機器人可視區域內，也不在極限L間隔或極限R間隔背后。不失一般性，設t在一個L間隔Gli（非極限L間隔）背后，如圖3（b）所示。在這個實例中，極限L間隔背后的邊界在R鏈上，其上至少存在一點與L鏈上的任意一點都不相互可視，這與街道的定義L和R相互弱可視矛盾。假設不成立，引理1得證。□

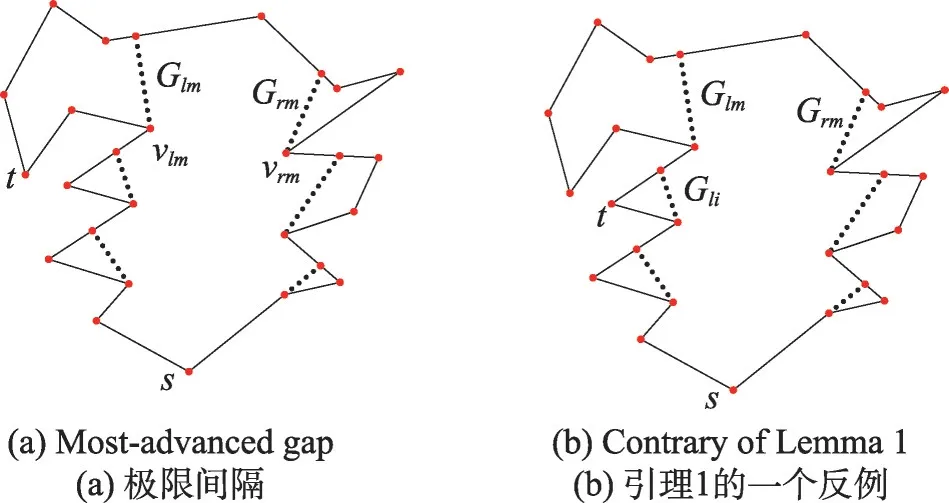
Fig.3 Most-advanced gap and its properties圖3 極限間隔及其特性

機器人在街道中搜索的時候，可能會遇到三種情況。第一種，終點t出現在機器人的可視區域中，毫無疑問，機器人這時直接走向終點t。第二種，可視區域內兩個極限間隔Glm和Grm，只有其中一個存在，如圖4（a）所示，機器人位于s點，此時只有Grm存在，根據引理1，機器人在該情況下直接走向現存極限間隔的關聯凹頂點。第三種，可視區域內兩個極限間隔Glm和Grm同時存在，如圖4（b）所示，機器人位于s點，由引理1可知，終點t可能在Glm后面，也可能在Grm后面，這種情況稱為漏斗，也是本研究要著重分析的一種情況。

在漏斗情況中，機器人會保持可視區域內極限間隔的更新。從漏斗的起點出發，依次連接曾經的極限L間隔的關聯凹頂點，可得到一條凸鏈，稱為該漏斗情況的L凸鏈；類似地，可以得到該漏斗情況的R凸鏈，如圖4（b）中虛線所示，s,vl1,vl2,vl3為L凸鏈，s,vr1,vr2,vr3為R凸鏈。

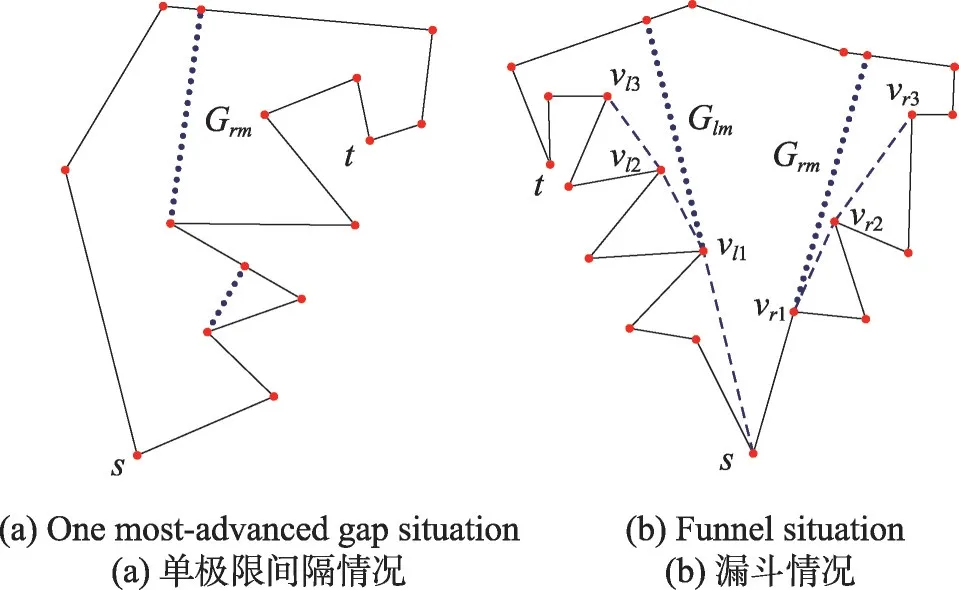
Fig.4 Two searching situations圖4 兩種搜索情況

引理2在漏斗情況中，L凸鏈和R凸鏈上各存在一個關鍵點，使得當機器人到達關鍵點時，當前漏斗情況結束。

證明當機器人到達L凸鏈或R凸鏈上的關鍵點時，漏斗情況會因如下兩種事件的發生而結束。第一種，極限L間隔和極限R間隔中的一個消失，如圖5（a）所示，消失的極限間隔的關聯凹頂點處的拐點射線與L凸鏈和R凸鏈分別交于a、b兩點，這兩點就是該漏斗情況中的關鍵點。第二種，極限L間隔和極限R間隔共線，此時原漏斗情況結束，一個新的漏斗情況出現，如圖5（b）所示，共線的兩個極限間隔的關聯凹頂點的公切線與L凸鏈和R凸鏈分別交于a、b兩點，這兩點就是原漏斗情況中的關鍵點。□

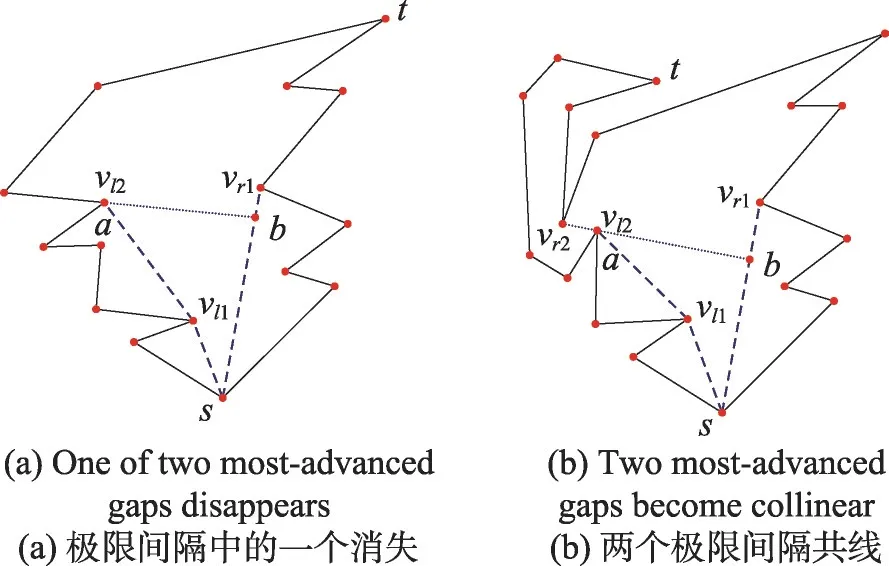
Fig.5 Two events for ending funnel situation圖5 漏斗情況結束的兩種關鍵事件

上述引理中提到的關鍵點稱為漏斗情況的關鍵點，由其定義可知，當機器人到達一條凸鏈上的關鍵點時，它可確認另一條凸鏈上的對應關鍵點。

引理3搜索街道的最短路徑SP在漏斗情況中的那一段，要么在L凸鏈上，要么在R凸鏈上。

證明在一個漏斗情況中，顯然SP經過其起點sf。從sf出發，由引理1可知，終點t在極限L間隔或極限R間隔背后，不失一般性，設其在極限L間隔背后，相反情況的分析與之類似。由上述假設可知，從sf到極限L間隔關聯凹頂點vlm的連線段必然屬于SP。接下來，隨著機器人的移動，極限間隔會持續更新，下面分兩種情況討論：第一種情況，直至該漏斗情況結束，第一個極限L間隔背后沒有任何極限R間隔出現，如圖4（b）所示，隨著極限L間隔的更新，SP在該漏斗情況中依次經過L凸鏈上每個極限L間隔的關聯凹頂點vl1、vl2、vl3。第二種情況，隨著極限間隔的更新，有一個極限R間隔出現在第一個極限L間隔背后，如圖5（b）所示，這個極限R間隔與當前的極限L間隔共線，此時該漏斗情況結束，SP在該漏斗情況中依次經過L凸鏈上每個極限L間隔的關聯凹頂點vl1、vl2。綜上，引理得證。□

定義4（精確鏈）漏斗情況的L凸鏈和R凸鏈中，SP覆蓋的那一條稱為該漏斗情況的精確鏈。

引理4在漏斗情況中，若機器人沿著L凸鏈或R凸鏈中的一條前進，當它到達關鍵點使得該漏斗情況結束時，它可以確認哪一條是精確鏈。

證明機器人沿著凸鏈前進，到達關鍵點使得漏斗情況結束，可分為如下兩種情況：第一種，極限L間隔和極限R間隔中的一個消失，如圖5（a）所示，顯然包含消失的極限間隔的關聯凹頂點的那條凸鏈不是精確鏈，與之對應的另一條為精確鏈。第二種，極限L間隔和極限R間隔共線，如圖5（b）所示，顯然包含共線極限間隔關聯凹頂點的那條凸鏈為精確鏈。□

4 雙弱感知能力機器人在線協作街道搜索算法

本章將根據上一章提出的街道搜索中的幾何特性，給出使用兩個弱感知能力機器人在線協作搜索街道的算法。算法的具體步驟如算法1和算法2所示。

算法1雙弱感知能力機器人在線協作街道搜索算法

算法2漏斗情況搜索算法

算法1是雙弱感知能力機器人在線協作街道搜索算法的主程序，其目標在于引導兩個機器人RT1和RT2從街道P的起點s出發，搜索并到達終點t。如前所述，在搜索的過程中，機器人可能會遇到三種不同的情況，分別為：終點t被發現、單極限間隔情況和漏斗情況。在終點t被發現以前，另外兩種情況可能會反復出現多次。當單極限間隔情況發生時，RT1和RT2徑直行至該極限間隔的關聯凹頂點，到達該凹頂點時，開始一個新的情況。當漏斗情況發生時，調用算法2專門處理這種情況。直到終點t被發現時，RT1和RT2徑直行至終點t。

算法2是雙弱感知能力機器人在線協作街道搜索算法的子程序，其目標在于處理搜索過程中較為復雜的漏斗情況。在漏斗情況中，由引理1可知，終點t要么在極限L間隔背后，要么在極限R間隔背后，但機器人不知道終點t具體在哪一個極限間隔背后。算法2讓RT1和RT2分別沿L凸鏈和R凸鏈前進，并保持各自可視區域內極限間隔及其關聯凹頂點的更新，直至某個機器人到達漏斗情況的關鍵點。由引理2可知，此時漏斗情況結束且關鍵點可被確認，再由引理3和引理4可知，此時精確鏈也可被確認。兩個機器人通過實時通信共享信息，共同行至精確鏈上的關鍵點。至此，兩個機器人將面對一個新的情況，或者是單極限間隔情況，或者是漏斗情況，或者是終點t被發現。

圖6給出了一個上述算法引導兩個弱感知能力機器人完成街道搜索的實例，圖中虛線表示漏斗情況中的凸鏈，箭頭表示機器人的行進路線。兩個機器人RT1和RT2從起點s出發，遇到第一個漏斗情況，根據算法2，RT1和RT2分別沿著該漏斗情況的L凸鏈和R凸鏈前進。RT1行至k點時，可視區域內極限R間隔更新，其關聯凹頂點更新為vr2，RT1行至vl1點時，可視區域內極限L間隔更新，其關聯凹頂點更新為vl2，類似地，RT2在行進過程中也保持可視區域內極限間隔及其關聯凹頂點的更新。當RT2行至d點時，極限L間隔消失，漏斗情況結束，RT2停在d點，確認該漏斗情況的關鍵點為d和vl2，精確鏈為R凸鏈。RT2將上述信息實時傳遞給RT1，RT1收到信息停在原地（c點），轉而走向d點。兩個機器人在d點會和，面對一個單極限間隔情況，一起從d點行至vr2點。兩個機器人再次面對一個單極限間隔情況，一起從vr2點行至vr3點。此時，兩個機器人遇到第二個漏斗情況，RT1和RT2分別沿著該漏斗情況的L凸鏈和R凸鏈前進。當RT1行至e點時，極限L間隔和極限R間隔共線，漏斗情況結束，RT1停在e點，確認該漏斗情況的關鍵點為e和vr4，精確鏈為R凸鏈。RT1將上述信息實時傳遞給RT2，RT2收到信息停在原地（f點）。兩個機器人行至vr4點會和，遇到第三個漏斗情況，與第一個漏斗情況類似，RT2行至i點時該漏斗情況結束。兩個機器人在i點會和，面對一個單極限間隔情況，一起從i點行至vr5點。兩個機器人再次面對一個單極限間隔情況，一起從vr5點行至vr6點。此時，終點t被發現，兩個機器人一起行至終點t。

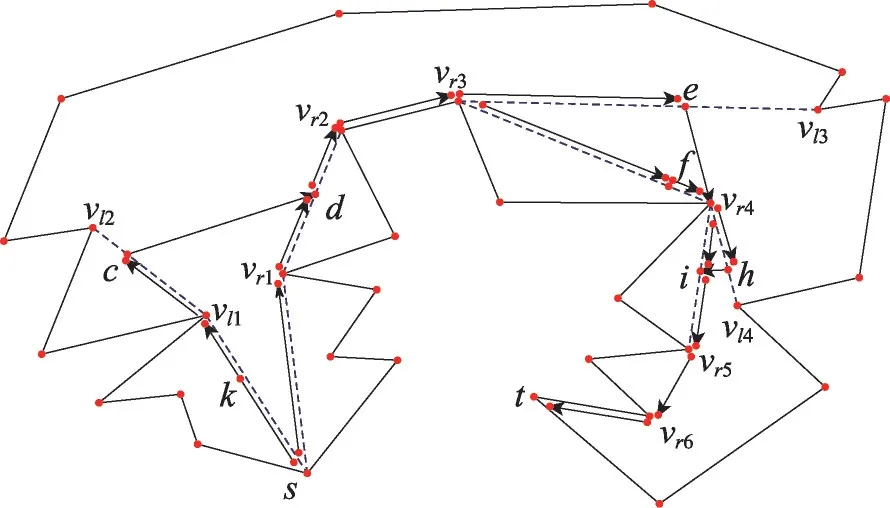
Fig.6 Instance of searching in street圖6 搜索街道的一個實例

5 算法效率分析

本章將通過競爭比分析算法的效率，并通過給出相匹配的競爭比下界證明算法的最優性。

5.1 算法的競爭比分析

由前文的分析可知，機器人搜索街道的過程中，只有漏斗情況會使機器人走出冗余路徑，進而影響算法的效率（競爭比）。因此，本節將分析的重點放在漏斗情況，為了準確界定漏斗情況的范圍，本研究將從漏斗情況起點出發，到漏斗情況精確鏈上的關鍵點結束，兩個機器人所走路徑圍成的區域稱為漏斗多邊形。如圖6所示，凸鏈s,vl1,c，線段和凸鏈s,vr1,d圍成的區域為漏斗多邊形。

定理1雙弱感知能力機器人在線協作街道搜索算法的競爭比為3。

證明如前所述，在街道搜索的過程中，機器人將面對三種情況，分別為終點t可見、單極限間隔情況和漏斗情況。在第一種情況中，本研究所提出的算法將引導機器人徑直行至終點t；在第二種情況中，本研究所提出的算法將引導機器人徑直行至極限間隔的關聯凹頂點。顯然，在這兩種情況中，機器人所走的路徑是最短路徑，算法的競爭比為1。

下面，分析本研究所提出的算法在漏斗情況中的表現。不失一般性，設精確鏈為漏斗情況的L凸鏈，相反情況的分析與之類似。為便于分析，給出一個滿足上述假設的漏斗多邊形實例，如圖7所示，其中sf為漏斗情況起點，a為精確鏈上的關鍵點，設A=凸鏈sf,vl1,vl2,vl3,a，B=凸鏈由算法2可知，RT1在該漏斗情況中所走路徑為A，RT2在該漏斗情況中所走路徑為B+D。結合兩個機器人到達各自所在凸鏈上的關鍵點的先后情況，可分如下三種子情況來討論：

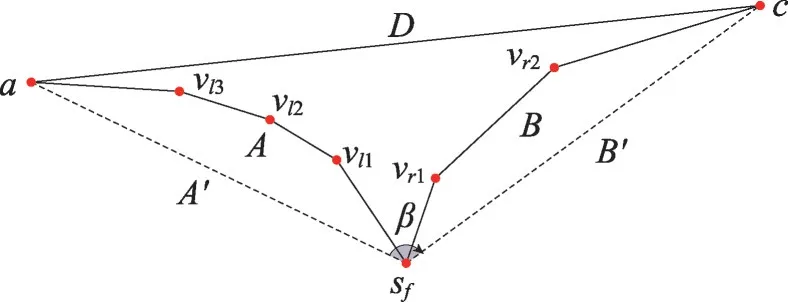
Fig.7 Instance of funnel polygon圖7 漏斗多邊形的一個實例

（1）RT1先到達L凸鏈上的關鍵點

在該情況下，RT1先到達a點，漏斗情況結束，此時RT2到達c點，然后RT1在a點等候，直至RT2經D到達a點與之會合。由兩個機器人速度相同且勻速前進可知，A=B。

（2）RT2先到達R凸鏈上的關鍵點

在該情況下，RT2先到達c點，漏斗情況結束，此時RT1尚未到達a點，然后RT1繼續沿L凸鏈前進直至到達a點，RT2經D到達a點，先到的機器人在a點等候，直至與另一個機器人在a點會和。由兩個機器人速度相同且勻速前進可知，A＞B。

（3）RT1和RT2同時到達各自凸鏈上的關鍵點

在該情況下，RT1到達a點，同時RT2到達c點，漏斗情況結束。后續與子情況（1）一致，因此A=B。

上述三種子情況覆蓋了精確鏈為L凸鏈的所有漏斗情況，由此可知，在該設定下，A≥B。

在△asf c中，D＜A'+B'，又A'＜A，B'＜B，可知D＜A+B。接下來，根據本研究第2章模型描述中所述式（1）計算競爭比。

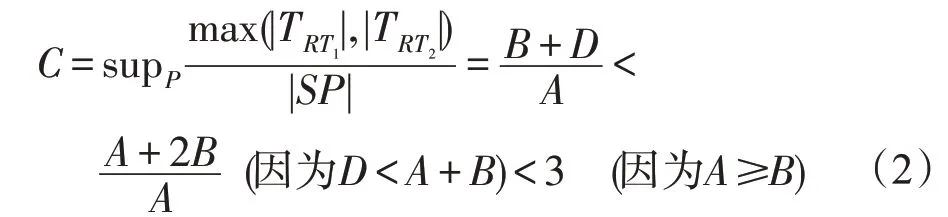
綜上，在街道搜索過程中，機器人可能面對的三種情況里，都滿足競爭比C＜3，因此，定理得證。□

5.2 競爭比下界分析

為證明本研究所提出算法的最優性，現給出競爭比下界的分析。

定理2任意使用兩個弱感知能力機器人在線協作搜索街道的確定性算法，其競爭比下界為3。

證明如前所述，在街道搜索的過程中，機器人將面對三種情況，分別為終點t被發現、單極限間隔情況和漏斗情況。在前兩種情況中，任意確定性算法都會引導機器人走最短路徑，因此不會對競爭比產生影響。在第三種情況中，為了限制住競爭比的上界，任意確定性算法都會引導兩個機器人分別向兩個極限間隔的關聯凹頂點前進，當一個機器人到達關鍵點使得漏斗情況結束時，兩個機器人會再次會和以面對后續情況，也只有這種情況會影響競爭比。由定理1證明中漏斗情況的分析可知，在精確鏈為漏斗情況的L凸鏈的前提下，A≥B，精確鏈為漏斗情況的R凸鏈的情況的分析與之類似。再結合競爭比計算公式，可知圖7中的D為決定競爭比的關鍵因素，當B=A，且D取最大值時，競爭比取得最大值。

如圖7所示，在△asf c中，根據余弦定理可知，這是一個關于β的增函數，當β=π 時取得最大值，Dmax=A'+B'。

根據上述分析，現構建一個特殊的漏斗情況，即L凸鏈與R凸鏈幾乎共線，可以想象該情況是通過增加β，拉伸D，壓平圖7所示的漏斗情況所得。此時，A趨近于A'，B趨近于B'，再設置該特殊情況下B=A。由競爭比計算公式可知，該特殊情況下競爭比C=(B+D)/A=3。

綜上，任意使用兩個弱感知能力機器人在線協作搜索街道的確定性算法在上述構建的特殊漏斗情況中，都不可能取得小于3的競爭比，因此，定理得證。

6 結束語

本研究分析了使用兩個弱感知能力機器人在線協作搜索街道的問題，通過構建模型并分析幾何特征，給出了競爭比為3的在線協作搜索算法，并通過給出相匹配的競爭比下界，證明了算法的最優性。本研究第3章給出的幾何性質同樣適用于街道模型中其他機器人搜索、探索問題的分析。本研究將搜索場景限制在街道模型，下一步將在更一般的多邊形場景中研究使用弱感知能力機器人在線協作完成搜索任務的高效算法；此外，將在模型中加入機器人視距的限制條件，研究相應的在線協作搜索算法。