考慮多禁止指向區域的航天器反步姿態機動控制
馬廣富,柳明旻,2,王靚玥,郭延寧
(1. 哈爾濱工業大學控制科學與工程系,哈爾濱 150001; 2. 上海航天控制技術研究所,上海 200233)
0 引 言
隨著航天技術的不斷發展,航天器結構愈發復雜,航天任務愈加多樣。執行科學任務的現代航天器裝配了數量較大、造價昂貴的敏感元件,如星敏感器、紅外望遠鏡、紅外干涉儀等[1]。這些敏感元件容易受到強光強熱天體的影響而失效,因此應考慮避免太陽光、地氣光、甚至月光等雜散光進入視野。同樣比如在在軌服務、空間攻防、碎片清除等空間任務中,還需要考慮目標對觀測視野的遮擋或者反射等。綜上各種因素以及其它約束的存在,導致了航天器在軌運行過程中存在某些禁止指向的姿態約束集。特別是在姿態機動過程中,為了確保該過程敏感器持續可用,必須在整個機動過程考慮禁止姿態指向約束集的情況下規劃可行姿態機動路徑及設計姿態控制律。需要注意的是,該禁止指向姿態約束集同航天器自身運動狀態、敏感器視野、光源或者目標位置等因素均相關,使得約束條件難以給出適于控制系統設計的通用描述。此外,考慮規避多禁止指向區域的航天器可行姿態機動區域是一個無界非凸的空間,對于相應的控制系統設計帶來了諸多難點。
近年來,各國學者針對考慮禁止指向區域的航天器姿態機動控制進行了廣泛的研究,并取得了一定的進展。目前,可以將解決此問題的方法分為路徑規劃法和人工勢函數法兩類。
路徑規劃是指在空間中設計一條可以規避禁止指向區域的姿態機動路徑,并施加跟蹤控制力矩使得航天器沿此路徑完成姿態機動。Singh等[2]針對Cassini號探測器設計約束監測法,并成功應用于Deep Space 1實際任務中,但該方法僅適用于某些特定任務自主姿態規劃,不具有普適性。Spindler[3]、Hablani[4]通過分析敏感器指向和明亮天體方向之間的幾何關系,在航天器機動操作前規劃一條沿禁止指向區域切線的可行姿態機動路徑,但其規劃過程未考慮航天器動力學特性,計算復雜。Frazzoli等[5]、Kornfeld[6]應用如遺傳算法等隨機算法解決了禁止指向約束等多種不同約束的姿態機動規劃問題,但其計算量受到約束種類、航天器姿態等多種因素的影響。Sun等[7]將禁止指向約束轉化為二次型函數,并將姿態機動問題轉化為二次型規劃問題,利用提出的一種最小秩方法求解最佳的機動路徑。但該方法計算量較大,需要多次計算獲得最優解。繆遠明等[8]將多約束條件下的姿態機動路徑規劃控制問題轉化為最優化控制問題,并采用基于比例微分控制編碼方法的粒子群優化算法進行求解以得到最佳的機動路徑,但其需要進行多次迭代搜索,規劃時間較長。路徑規劃方法通常可以獲得最佳的機動路徑,但其計算量較大、計算時間較長,故該方法更適用于離線或慢變的簡單約束任務場景,不宜用于考慮多種復雜約束的實時在線航天器自主姿態機動任務。
勢函數法最初應用于機器人在操作空間的路徑規劃問題,其具有結構簡單,易于實時控制、計算簡單的優點,目前已被應用于天體軟著陸、飛行器編隊飛行、航天器自主交會和路徑規劃等航天領域[9]。勢函數法應用于規避禁止指向區域的航天器姿態機動也取得了一定的研究成果。McInnes[10-11]設計了基于高斯函數的人工勢場函數以規避太陽光的照射,并將其引入李亞普諾夫函數中進行大角度姿態機動控制律的設計。然而由于其采用歐拉角描述航天器的姿態及其約束,可能導致姿態機動過程中存在奇異問題。鄭重等[12]在此基礎上采用四元數描述航天器的禁止姿態約束以及高斯人工勢場函數,并分別對有無擾動下閉環系統的穩定性進行了分析。張景瑞等[13]基于禁止姿態作用范圍設計一種可以規避局部極小值的勢函數,并利用反步法對控制律進行設計。崔祜濤等[14]通過在單位球面上建立視線軸對應的導航函數設計了一種基于反步法的指向約束姿態機動控制律,并對控制律進行改進使其同時滿足輸入受限和常干擾抑制。Kim等[15]基于四元數描述方式對空間中多種姿態約束進行參數化凸描述,并利用凸優化方法對航天器的控制律進行設計。Lee等[1]利用該參數化約束描述設計了一種凸對數勢函數,并分別根據李亞普諾夫直接法和改進反步法設計了模型獨立及模型非獨立兩種姿態控制律。該方法能夠滿足多種姿態約束的同時在任意初始條件下保證系統的全局收斂性,但其設計的對數勢函數缺乏較明確的物理意義。同時,Lee等[17]還應用此約束描述將問題轉化為凸優化求解問題,并利用高斯偽譜法求解了考慮多種姿態約束下的時間能量最優控制。馮振欣等[18]針對微小衛星存在多重指向約束的姿態控制問題進行研究,在考慮微小衛星計算能力有限的情況下,提出了一種基于對數型勢函數的航天器姿態機動控制律,并同時解決了角速度受限問題。
由于現有的勢函數存在局部極小值問題或缺乏較為明確的物理意義,本文在構造通用的禁止指向區域凸約束集的基礎上提出了一種新型具有明確物理意義的凸勢函數,能夠有效地避免傳統勢函數中的局部極小值問題。進一步地,考慮多個禁止指向區域,設計一種基于反步法的姿態控制律,以實現航天器的自主姿態機動。通過典型數值仿真校驗了所設計控制算法的有效性。
1 航天器模型建立
本文以剛體航天器為研究對象,采用四元數描述航天器的姿態,根據剛體動量矩定理以及剛體復合運動關系建立航天器的動力學和運動學模型如式(1)、式(2)所示:
(1)
(2)
其中,
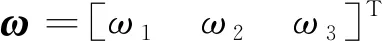
(3)
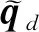
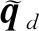
(4)
其中,
2 禁止姿態約束描述
航天器上裝配有各類敏感器,在其姿態機動過程中,應避免太陽等光源進入敏感器視場,以保證敏感器的正常使用,將這類約束稱為禁止指向區域。不失一般性,以太陽為例,其它光源的描述與其相同,其約束示意圖如圖1所示。其中,xi為航天器指向太陽方向的單位向量在慣性系的投影,y代表航天器敏感器視線方向的單位向量在本體系下的投影,θ代表該敏感器的視場大小。
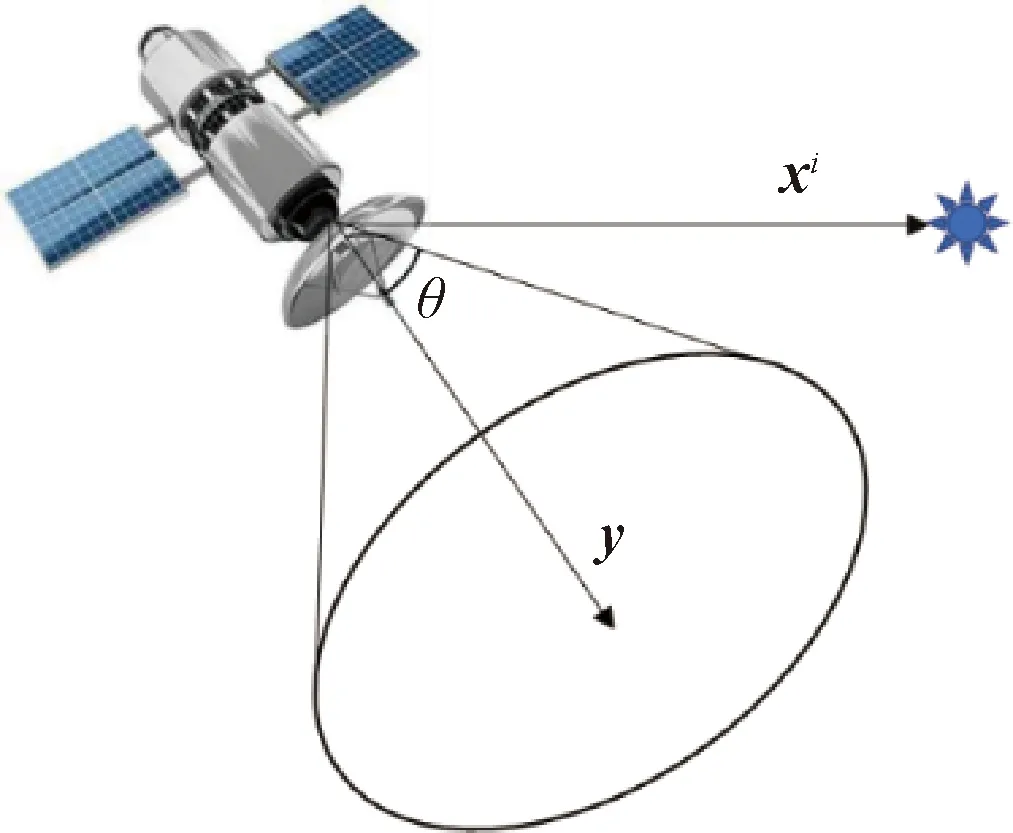
圖1 禁止姿態示意圖
當航天器滿足禁止指向約束時,光源未進入敏感器的視場范圍,即代表方向的兩個單位向量在同一坐標系下投影的夾角應大于敏感器的視場角,其數學表達式如式(5)所示:
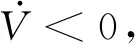
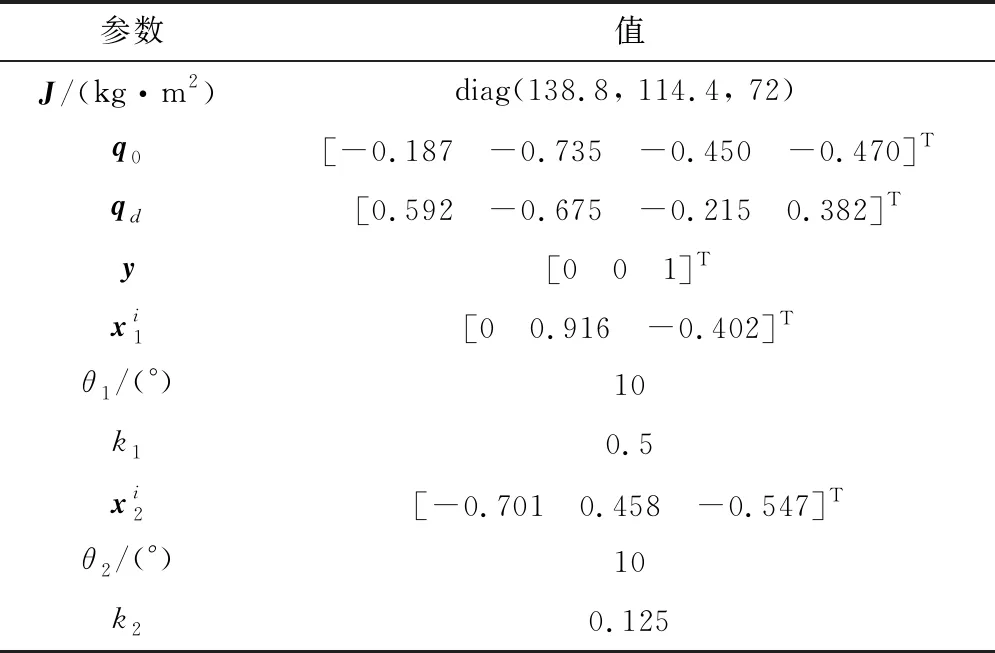
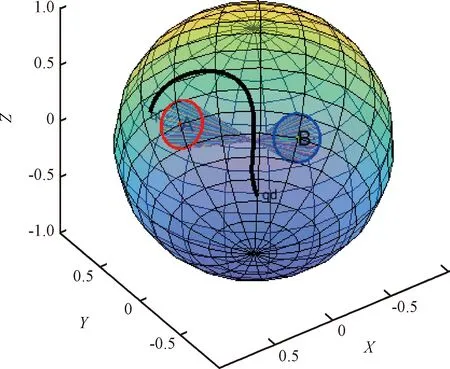
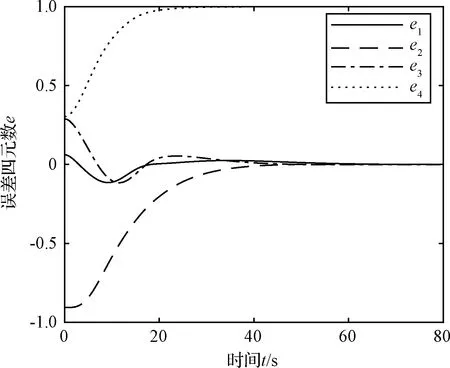
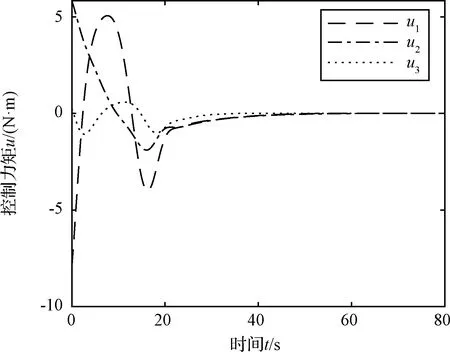
xi·yi (5) 式中:yi代表敏感器視線方向的單位向量在慣性系下的投影。 敏感器視線方向在慣性下的投影與航天器的姿態相關,實時變化,不能通用地描述禁止指向區域。因此,需要將敏感器視線方向在慣性系下的投影yi轉化為其在本體系的投影y,轉換關系如式(6)所示: 2(qTy)q+2q4(y×q) (6) 將式(6)代入式(5),并整理可得: 2qTyqTxi-qTq(xi)Ty+ (7) 對式(7)進行代數變化,轉換為如式(8)所示的矩陣形式: (8) 其中,a=xiyT+y(xi)T-((xi)Ty+cosθ)I3,b=(xi)×y,d=(xi)Ty-cosθ 從矩陣A的定義可以看出,A為對稱矩陣,其特征值均為實數。同時,由于A為非正定矩陣,式(8)描述的約束集為非凸集合。非凸約束集在尋找可行機動路徑時不僅會增加計算的復雜性,而且會使姿態陷入局部極小值而不能到達期望姿態。因此,需要對該非凸約束集進行處理轉化為凸約束集,并將約束中的姿態四元數轉化為誤差四元數的形式,為后續勢函數以及控制律的設計提供基礎。 定理1.禁止姿態約束集式(8)可以轉化為如式(9)所示的凸約束集形式: (9) 證. 太空中的光源并非只有太陽,故應考慮姿態機動時存在多個禁止指向區域。實際航天器中敏感器分布在多個軸向,即航天器不止單軸受到禁止指向約束。但由于增加指向軸約束會使姿態機動的可行空間受到限制,求解復雜,故本文提出的控制律僅考慮航天器僅單軸受到多禁止指向約束,但延伸應用到多軸多禁止指向約束任務同樣行之有效。 在第2節對約束集合凸化的基礎上,本文提出一種新型的凸勢函數,該勢函數具有明確物理意義,且僅在期望姿態處具有全局極小值。考慮多禁止指向約束構建的勢函數如式(10)所示: (10) 其中,ki>0為姿態禁止區域在勢函數中代表的權重。此勢函數中,分子代表了當前姿態與禁止指向區域的距離,距離越近,分子越小,產生的排斥力越大。而分母則描述期望姿態的吸引作用,姿態距離期望姿態越近,分母值越小,勢函數的排斥作用越小。當航天器姿態到達期望姿態時,勢函數值為0,即完成了姿態機動。 證. 下面證明該勢函數是凸函數,通過對其海森矩陣(二階梯度)的正負定性來判斷其是否為凸函數,當其海森矩陣為正定矩陣時,該函數為凸函數。 該勢函數的一階梯度如式(11)所示: (11) 求導并整理得到二階梯度如式(12)所示: (12) (13) 反步法是一種遞歸設計方法,其設計思想是遞歸地構造李亞普諾夫函數設計控制律,能夠保證系統狀態漸近收斂到平衡狀態。式(1)、式(4)構成的航天器姿態誤差模型是一個標準的級聯系統[19],因此可以基于反步法對該系統的姿態機動控制律進行設計。 反步法控制律的設計分為兩步。 第一步,設計虛擬角速度控制律使航天器的運動學分系統穩定。該分系統的李亞普諾夫函數即為式(10)所示的勢函數,對其求取時間的全導數,如式(14)所示: (14) 式中:ωs為待設計的虛擬角速度控制律。 為保證該分系統漸近穩定地收斂到平衡狀態,設計ωs如式(15)所示 (15) 式中:α>0為虛擬角速度控制律的設計參數。 此時,滿足 在式(15)控制律作用下,該分系統漸漸穩定。 第二步,設計控制力矩使得虛擬角速度ωs趨近于真實角速度且漸近收斂于平衡狀態,即使航天器的動力學分系統穩定。 定義虛擬狀態量 (16) 構造李亞普諾夫函數為 (17) 對其求取時間的全導數可得: (18) (19) 為保證系統的漸近穩定性,設計控制律 (20) 將式(15)代入式(20)對控制律進行整理,得到利用反步法設計的基于勢函數的航天器姿態控制律如式(21)所示: (21) 式(21)所設計的控制律由三項組成,其中第一項為航天器動力學非線性抵消項,第二項為虛擬角速度跟蹤誤差項,第三項為姿態誤差控制項。在該控制律的作用下,航天器能夠滿足禁止指向約束的同時從任意初始狀態機動到期望狀態。 為校驗該控制律的可行性對其進行數值仿真。本節考慮在空間中存在兩個光源不能進入敏感器的視場,利用式(21)所示的控制律進行控制,驗證其在完成姿態機動目的時能夠滿足姿態約束。 當航天器姿態誤差較大或距離禁止指向區域較近時,由此控制律得到的控制力矩往往較大,雖然能夠使航天器姿態快速機動到期望姿態及迅速遠離禁止指向區域,但由于航天器的實際執行機構具有物理限制,因此需要考慮控制受限問題。通過合理選擇控制律中各項參數,使得控制律滿足幅值限制。 在航天器誤差角速度有界的假設下,航天器的控制力矩幅值滿足 (22) 具體的仿真條件如表1所示。 表1 仿真參數 本仿真算例中,控制力矩的幅值約束為10 Nm,選取控制律參數為α=0.54,β=30,搭建Matlab中的Simulink模型進行仿真,并繪制仿真結果圖。航天器姿態機動過程中的誤差四元數變化、誤差角速度變化、控制力矩變化分別如圖2、圖3、圖4所示。 為更直觀地觀察航天器姿態機動路徑對禁止指向區域的規避,在三維球體上繪制出禁止指向區域以及航天器敏感器指向的機動路徑圖,如圖5所示。 圖5 航天器姿態機動軌跡三維示意圖 其中,A錐體表示光源1的禁止指向區域,B錐體代表光源2的禁止指向區域。粗實線代表敏感器指向從初始姿態q0到期望姿態qd的機動路徑。 從圖2、圖3可以看出,航天器誤差四元數以及誤差角速度的調節時間在60 s左右,系統的超調量和穩態誤差范圍合理。但由于控制律設計采用反步法,系統在到達平衡狀態附近的控制作用較弱,趨向于平衡狀態的時間較長。同時,圖4中控制力矩的幅值始終小于10 N·m,滿足飽和約束,但控制幅值受限帶來了系統的調節時間較長的不利影響。 圖2 航天器誤差四元數仿真結果 圖3 航天器誤差角速度仿真結果 圖4 航天器控制力矩變化圖 從圖5可以看出,航天器的姿態機動路徑在靠近光源1或光源2的禁止指向區域時,由于受到勢函數的排斥作用而偏離最佳機動路徑,具體表現為在禁止指向區域附近的機動路徑為遠離該區域的兩條弧線。這與控制力矩仿真圖中出現兩次尖峰相符合。同時禁止指向區域權重的大小不同以及距離期望姿態指向的遠近不一,光源1產生的排斥力要強于光源2產生的排斥力,控制力矩仿真圖4中表現為第一次尖峰的峰值大于第二次尖峰幅值,與仿真圖5中弧線規避路徑的半徑大小不同相對應。 本文在結合物理意義明確的凸勢函數基礎上設計了一種基于反步法的航天器姿態機動控制律,能夠快速穩定準確地完成航天器姿態機動過程的同時實現多禁止指向區域的規避。仿真結果表明了該算法的有效性。 未來將著手于航天器空間中受到禁止指向區域、強制指向區域等多種約束條件下的姿態機動控制,以及對目前控制方法進行改進加快穩態值附近的控制作用以獲得更佳的控制效果。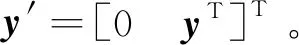
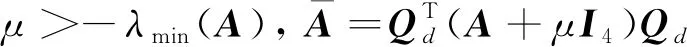
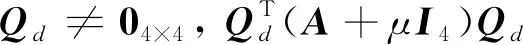
3 基于勢函數的反步法控制律
3.1 勢函數設計
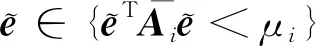
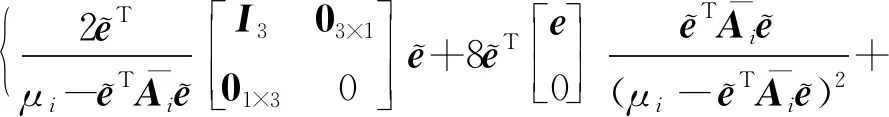
3.2 基于反步法的航天器姿態機動控制律
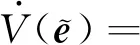
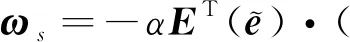
4 數值仿真


5 結 論

