一類具有非線性邊界條件的擬線性拋物方程的爆破

丁俊堂,安蕾

(山西大學 數學科學學院,山西 太原 030006)

0 引言

在過去的十多年中,人們對非線性拋物方程的爆破解和整體解做了很多研究,我們向讀者推薦文獻[1-5]及其中的參考文獻。在本文中我們的興趣集中在以下類型的一類擬線性拋物問題的爆破現象:

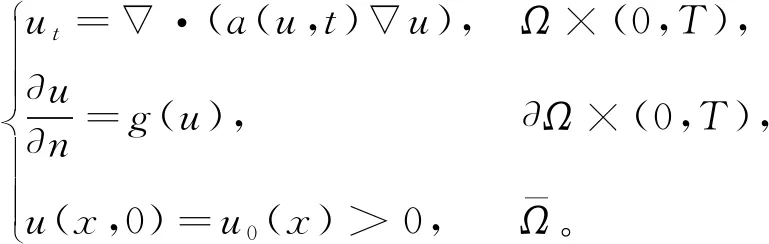
(1)

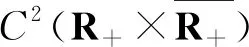
關于具有非線性邊界條件的非線性拋物方程解的爆破問題有大量文獻(見文[8-25])。為了研究問題(1)的爆破解和整體解,我們主要關注了文[21-22]。在文[22]中，Yin研究了以下問題的爆破解和整體解:

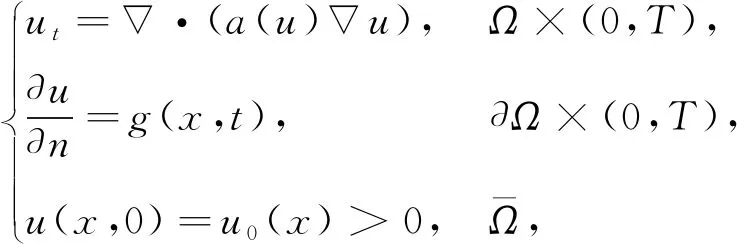
(2)

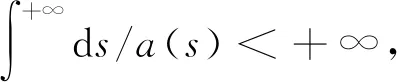
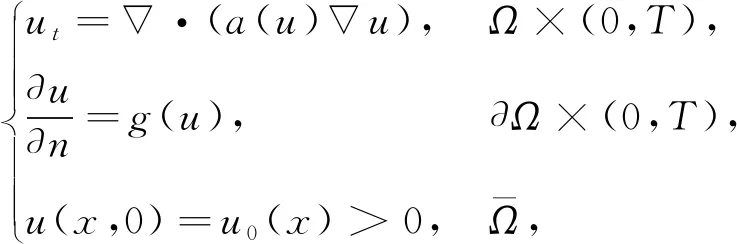
(3)

這里Ω?RN(N≥2)是一個有界區域,?Ω是光滑的。在一些合適的假設下,他們證明了如果

或

且

a(s)g2(s))< +∞,

那么(3)的解在有限時刻爆破;如果

且

a(s)g2(s))= +∞,

那么(3)的解整體存在。他們的研究在很大程度上依賴于使用比較原理。

本文研究了(1)的爆破解和整體解。我們注意到問題(1)中的a(u,t)不僅依賴解u,而且還依賴于時間變量t,而在問題(2)和(3)中a(u)只依賴于解u,因此文[21]和[22]中的研究方法不適用于研究問題(1)。和文[23,25]一樣,我們現在使用拋物極值原理和一階微分不等式技術來研究問題(1)。使用這種研究方法的困難在于需要構造一些合適的輔助函數。由于文[23,25]中已有的輔助函數不適合于問題(1)的研究,所以必須構造一些新的輔助函數來完成本研究。

1 爆破解

在本節中我們建立一些條件來保證爆破解存在。我們構造如下兩個輔助函數:

(4)

(5)

這里我們假定

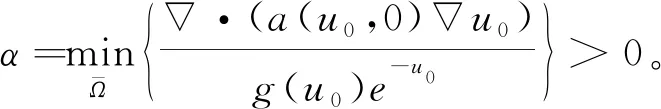
(6)

注意到

這就保證了P有反函數P-1。利用輔助函數(4)和(5)我們能獲得下面的定理1。

定理1 設u是(1)的一個古典解。假定初值u0滿足(6)。 此外我們假定函數a和g滿足

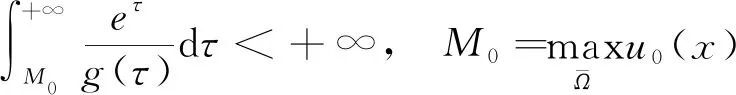
(7)

以及對任意(s,t)∈R+×R+,

(8)

[a(s,t)(g′(s)-g(s))]s-a(s,t)(g′(s)-g(s))≥0。

(9)

那么u在某個有限時刻T爆破且

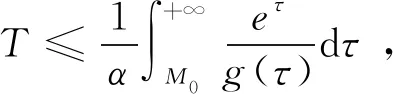
(10)

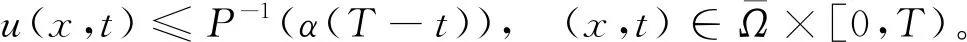
(11)

證明對輔助函數H直接計算可得

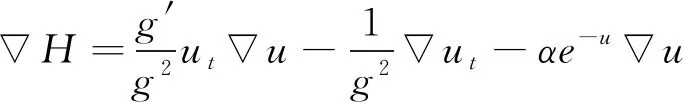
(12)

和

(13)

借助于(1)的第一個方程我們獲得

(14)

利用(13)和(14)我們推出

aΔH-Ht=

(15)

由(12)可得

(16)

將(16)代入(15)我們有

(17)

由(1)的第一個方程可得

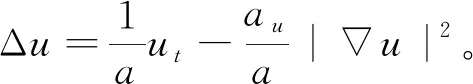
(18)

把(18)代入(17)中我們推出

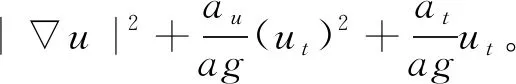
(19)

由(4)可得

ut=-gH+αge-u。

(20)

我們把(20)代入(19)推出

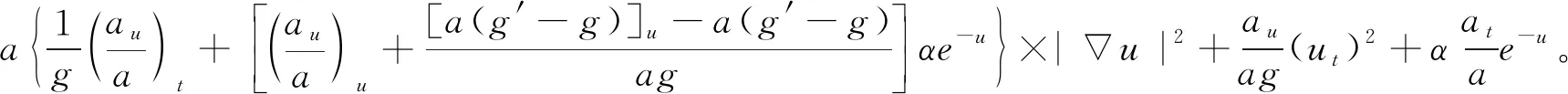
(21)

由假設(8)和(9)我們可知等式(21)的右端是非負的。因此我們有

(22)

利用(1)的邊界條件可得

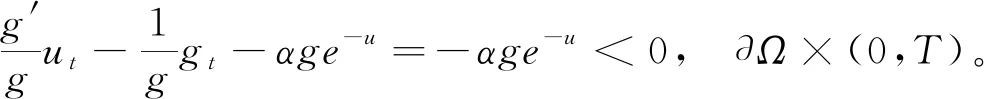
(23)

根據(6)可知

(24)

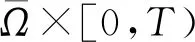
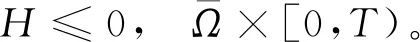
由此我們得到下列一階微分不等式

(25)

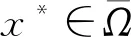
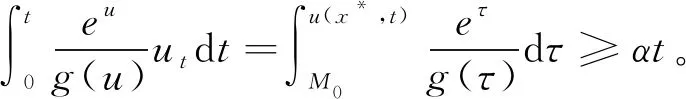
(26)

假設(7)和不等式(26)保證了u在有限時刻T爆破。為了獲得爆破時刻T的一個上界,我們對(26)取極限t→T可得

由于u在有限時刻T爆破,故對每一個固定的x我們對(25)從t到T積分就有

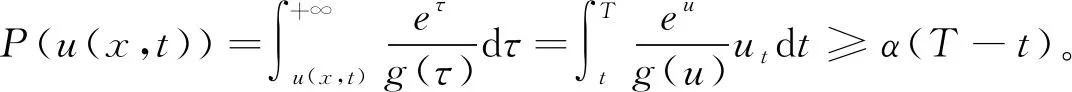
(27)

從(27)可得

u(x,t)≤P-1(α(T-t)) 。

定理1得證。

2 整體解

本節中我們對非線性函數a,g和u0建立一些條件以保證(1)的解整體存在。我們定義輔助函數

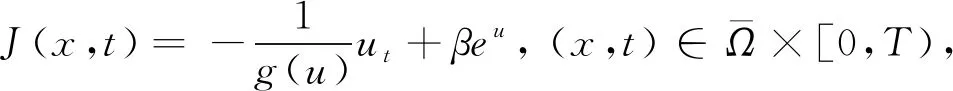
(28)

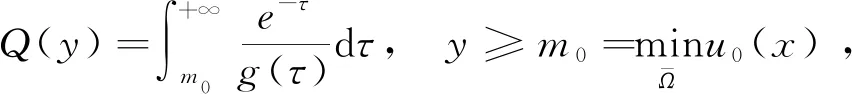
(29)

這里我們假定

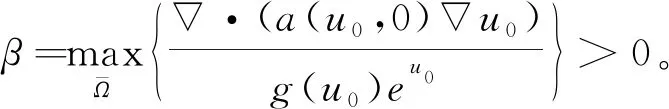
(30)

現在我們有

這就保證了函數Q的反函數Q-1存在。 我們的主要結果如下。

定理2 設u是(1)的一個古典解。 假定初值u0滿足(30),函數a和g滿足

(31)

和對任意(s,t)∈R+×R+,

as(s,t)≤0,at(s,t)≤0,

(32)

[a(s,t)(g′(s)+g(s))]s+a(s,t)(g′(s)+g(s))≤0,

(33)

那么u整體存在且

u(x,t)≤Q-1(βt+Q(u0(x)))。

(34)

證明對輔助函數J(x,t)使用(12)-(19)的推理過程,我們可得

(35)

假設(32)和(33)保證了等式(35)的右端是非正的。因此我們有

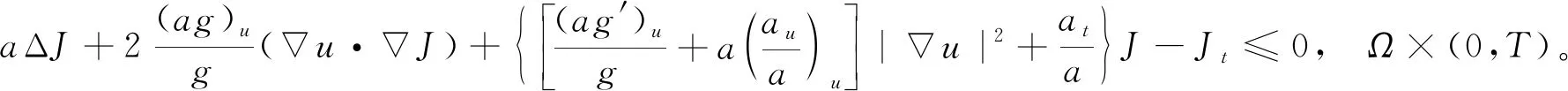
(36)

重復(23)的計算可得

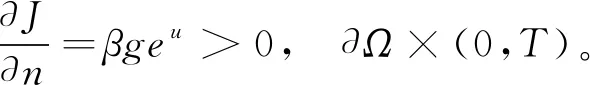
(37)

根據假設(30)我們有

(38)

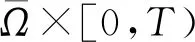
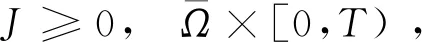
由此獲得下列一階微分不等式

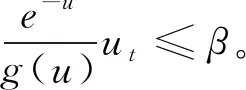
(39)

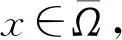
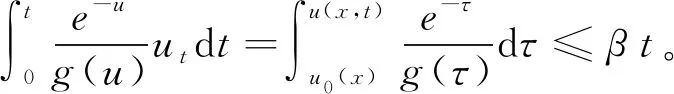
(40)

利用(40)我們有

因此我們推出

u(x,t)≤Q-1(βt+Q(u0(x)))。

這就是整體解u的一個上估計。 定理2得證。

3 應用

當a(u,t)≡a(u)時定理1和定理2仍然成立,因此在這篇論文中我們獲得的定理1和定理2可以適用于問題(3)。在這個意義下我們的結果是文[21]中結果的推廣。下面我們給出兩個例子來說明定理1和定理2的應用。

例1 設u是下列問題的一個古典解

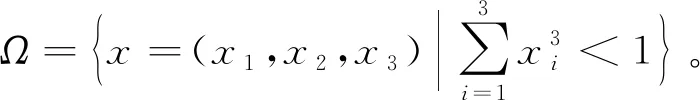
容易驗證條件(7)-(9)成立。由(6)我們有

根據定理1可知u在有限時刻T爆破且

例2 設u是下列問題的一個古典解

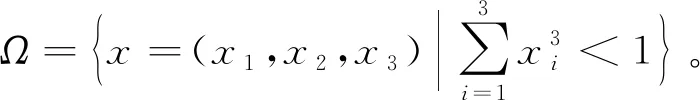
容易驗證條件(31)-(33)成立。由(30)可得

根據定理2可知u整體存在且