毫米波MIMO系統中部分連接型混合預編碼設計

鄭興林，王 月，劉 偉

重慶郵電大學 通信與信息工程學院，重慶 400065

1 引言

毫米波大規模多輸入多輸出（Multiple-Input Multiple-Output，MIMO）系統，由于其高帶寬和高頻譜效率而成為下一代通信系統的關鍵技術[1-4]。例如，在30 GHz 的載波頻率下，波長為10 mm，這使得大量天線可以封裝在微小區域中。大規模天線陣列能夠帶來較高的波束賦形增益，以補償毫米波信號的高路徑損耗[4]。然而，在傳統的MIMO 系統中，傳輸預編碼通常只考慮數字域，并且需連接與天線數量相同數目的射頻（Radio Frequency，RF）鏈路[5-8]。毫米波系統結合大量天線陣元，抵消路徑和穿透損耗，由于硬件成本和功耗很高，傳統全數字預編碼在毫米波通信系統中是不可行的。為了解決這一問題，文獻[9]提出了混合預編碼的概念，用兩階段的預編碼器代替傳統純數字預編碼器。首先用小型數字預編器對信號進行處理，然后用大型模擬預編碼器得到高波束形成增益。

目前混合預編碼方案有全連接（Fully-Connected，FC）和部分連接（Partially Connected，PC）結構[10]，發送端系統模型如圖1 所示。在全連接結構中，每條RF 鏈通過大量移相器與所有天線連接，以最大化實現可達到的傳輸增益，然而將會導致高能耗[11]。相比之下，部分連接結構需要較少數量的移相器，雖然性能有所損失，但能帶來更高的能源效率[12]。對于全連接型混合預編碼的研究，文獻[13]提出了基于流形優化的交替算法（MO-AltMin Algorithm，MO-Alt）來接近全數字預編碼器的性能，然而，模擬預編碼器的更新涉及到線性搜索算法，嵌套循環將減慢整個求解過程，復雜度很高。文獻[14]采用DFT碼本構成模擬預編碼矩陣，大大降低了算法復雜度，但由于模擬預編碼是從DFT 碼本集中選取，沒有很好的匹配信道，性能增益小。對于部分連接型混合預編碼，由于其能耗更低，是近年來研究熱點。文獻[13]利用半定松弛（Semidefinite Relaxation，SDR）思想，提出一種交替最小化算法，通過凸優化工具箱（Convex optimization toolbox，CVX）求解數字預編碼器，每一次迭代需要借助標準凸優化算法來求解半定規劃（Semidefinite Programming，SDP）問題，導致復雜度較高。文獻[15]中利用注水算法設計數字預編碼，將模擬預編碼設計等效為單天線功率約束下單流最優發射機波束形成問題，復雜度很高。

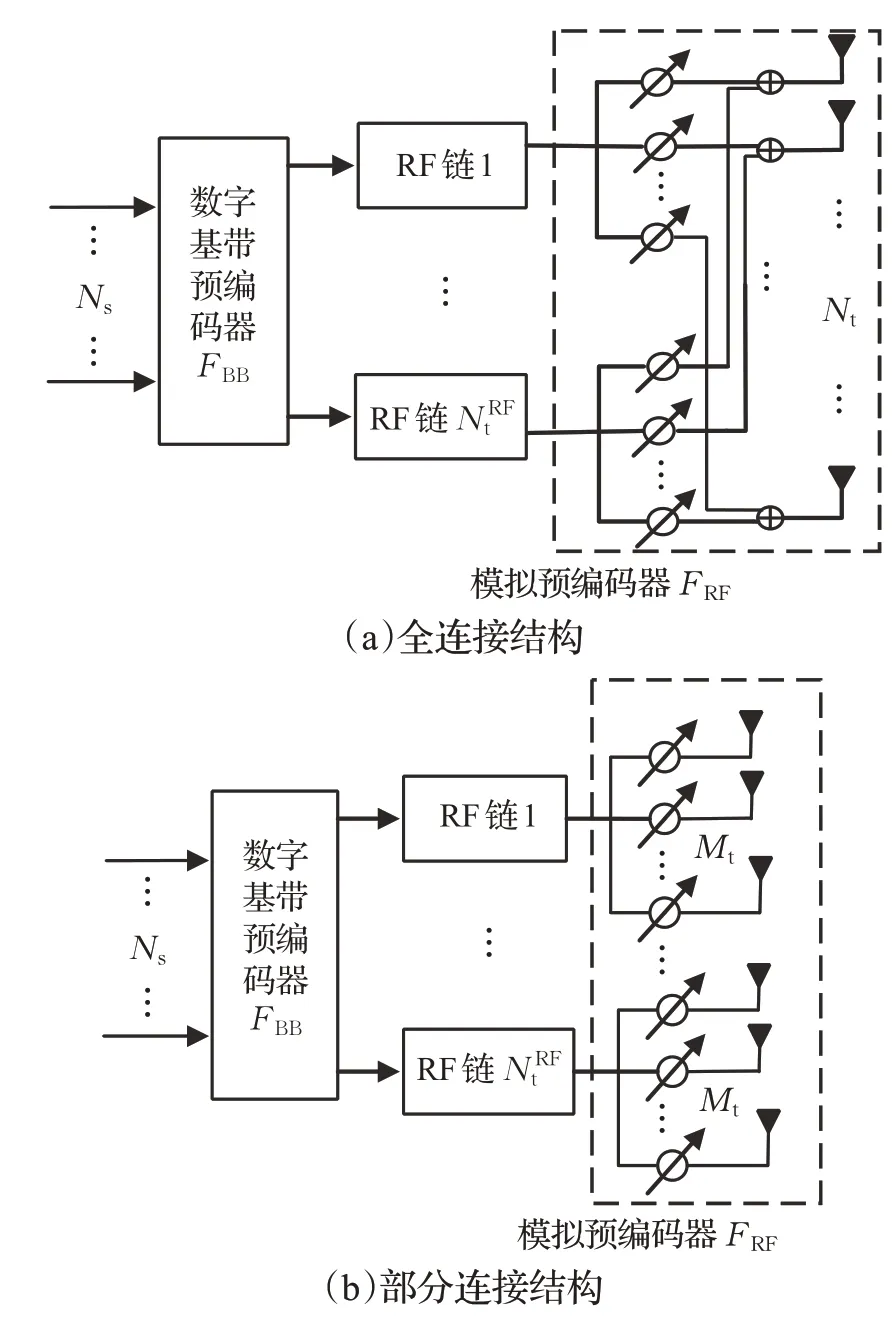
圖1 發送端混合預編碼系統模型

基于上述分析，考慮工程實際應用，本文研究部分連接型混合預編碼。證明了信道右奇異值向量的相位角來初始化模擬預編碼器的可行性。為了獲取更優的性能和更高的能源效率，設計了一種基于SVD 的交替迭代（Alternating Iterative SVD，Alt-ISVD）混合預編碼算法。仿真結果表明，所提算法隨著信噪比增加，性能更加優于傳統部分連接型算法，且復雜度與文獻[15]提出的算法相比明顯降低，與傳統正交匹配追蹤（Orthogonal Matching Pursuit，OMP）算法[8]相比擁有更高的能源效率。

2 系統模型與信道模型

2.1 系統模型

考慮下行鏈路毫米波單用戶系統，基站（Base Stations，BS）側配備Nt根發射天線，發射端射頻鏈路數為NtRF，系統模型如圖1（b）所示。每條RF 鏈路僅與一個獨立的子陣列相連，且每個獨立子陣列均包含M根天線，即從圖1 可以看出，當基站配有Nt根天線，全連接型中模擬域需個移相器與所有天線相連，而部分連接型中模擬域只需Nt個移相器與部分天線相連，因此采用部分連接結構，硬件成本和功耗更低，更貼切實際應用。發送端有Ns條數據流發送，數據流s∈?Ns×1首先在數字域經數字基帶預編碼器進行預處理，然后在模擬域經過模擬預編碼器調相到各天線陣元，形成波束賦形增益，經過兩階段預編碼器，最終的發送信號為：

式中，發送信號s應滿足，模擬預編碼器和數字預編碼器應滿足總的功率限制Ns。其中，E[?]表示求期望，I為單位矩陣表示Frobenius范數。接收端經過解碼處理后信號為：

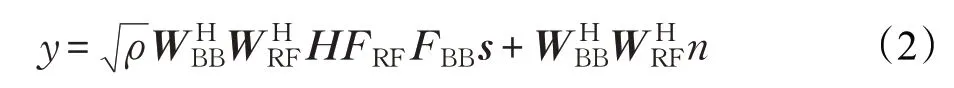
式中，ρ為接收功率，WBB和WRF分別表示為接收端數字合并器和模擬合并器。FRF和WRF應滿足單模限制，即維毫米波幾何信道矩陣。分布的加性高斯噪聲。其中，(?)H表示取共軛轉置，Nr為移動臺（Mobile Station，MS）配有的天線數目。

2.2 信道模型

考慮到毫米波信道的有限散射特性，本文采用擴展的Saleh-Valenzuela簇信道模型[9]，窄帶毫米波信道矩陣H表示為：

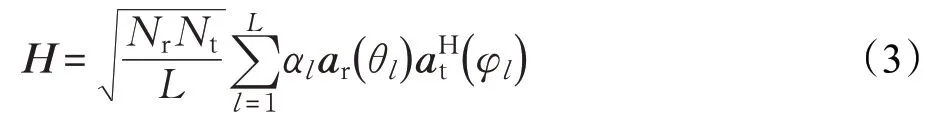
式中，L為系統傳播路徑數，且每條簇能夠產生一條傳播路徑。αl為服從CN(0,)分布的第l條路徑的復增益，矢量ar(θl)和at(φl)分別定義為接收和發送陣列矢量，其中，θl∈[0,2 π]和φl∈[0,2 π]是第l條徑的到達和離開方位角。當收發端天線陣列為均勻線陣（Uniform Linear Array，ULA）時，發送和接收天線陣列歸一化響應矢量表示如下：

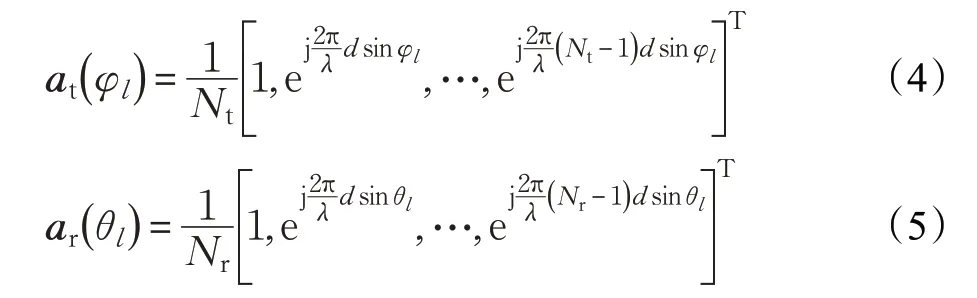
式中，λ為載波波長，d為天線間距。

2.3 問題描述

本文設計混合預編碼的目標是減小算法復雜度，提高系統頻譜效率。系統頻譜效率表示為：

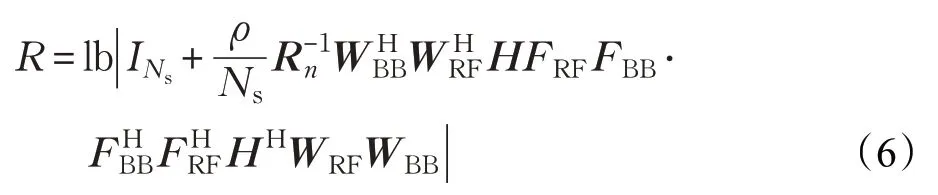
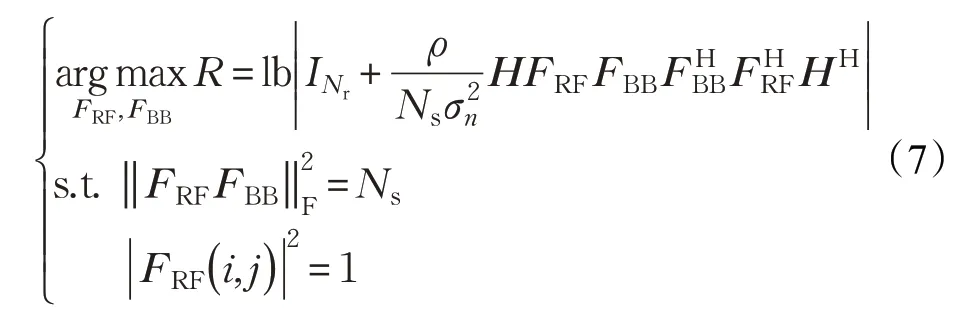
發送端預編碼器和接收端合并器優化問題的數學公式相似，只是預編碼矩陣設計需要考慮功率約束，因此本文主要研究發送端預編碼器的設計。

首先對H進行奇異值分解H=UΣVH，其中，U和V分別為H對應的左奇異值矩陣和右奇異值矩陣，Σ為特征矩陣。將H=UΣVH代入式（7）得：

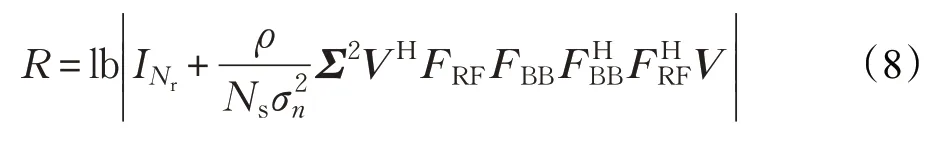
對Σ,V進行分塊表示：

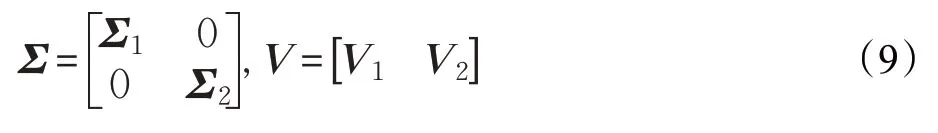
式中，Σ1為Ns×Ns維對角陣，V1的維度為Nt×Ns，最優無約束預編碼器Fopt=V1，將式（9）代入式（8）中，則式（8）中部分項可以表示為：

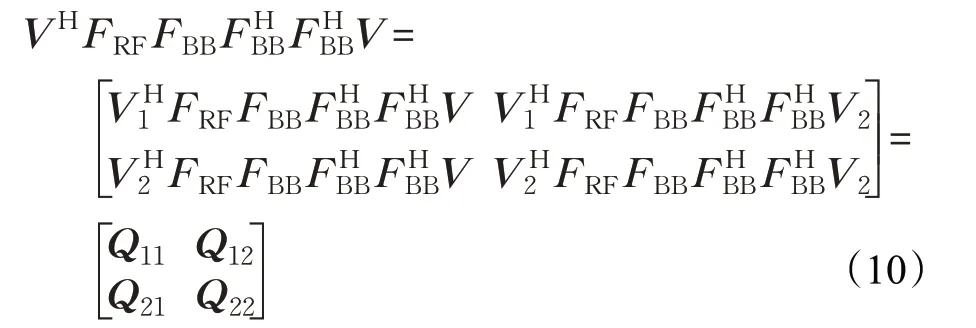
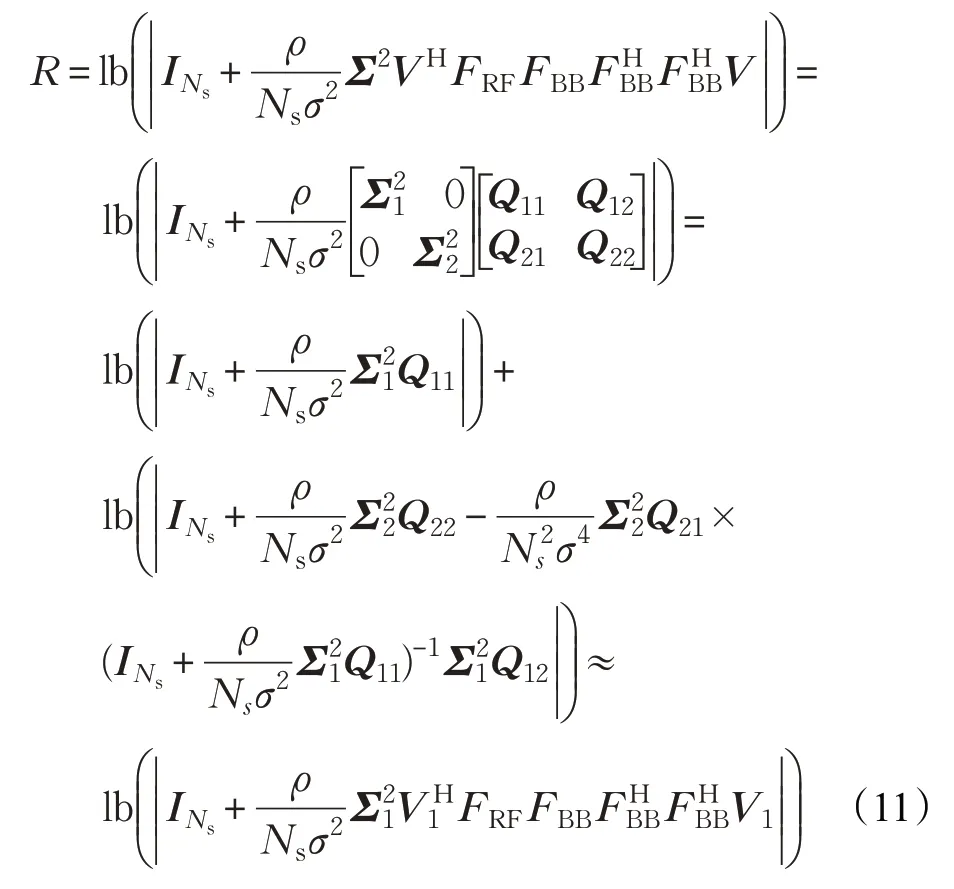
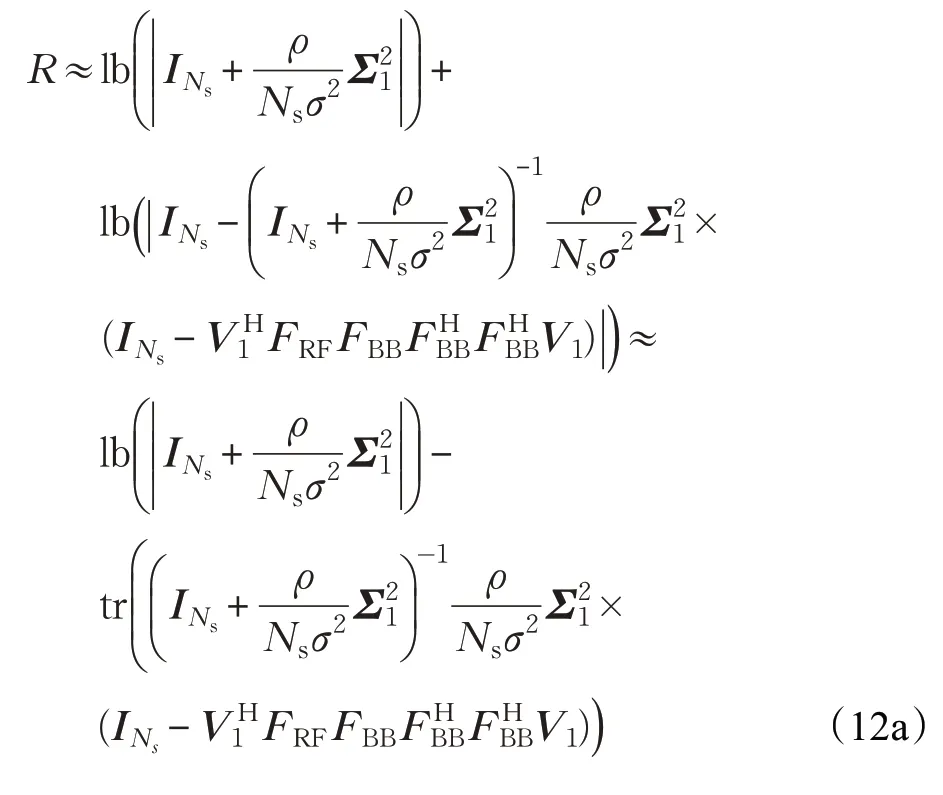
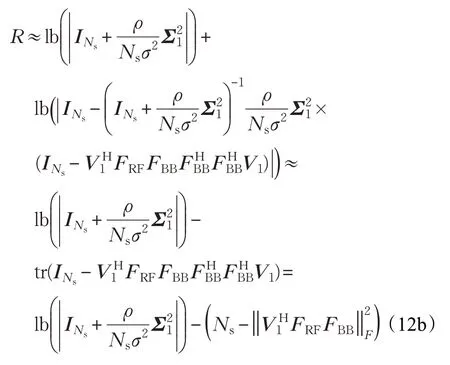
式（12a）表示應用：lb(|INs-X|)≈lb(1-tr(X))=-tr(X),其中，tr(?)表示矩陣或矢量的跡。式（12b）表示采用高有效信噪比近似，即由式（12）得，獲取最大化R等價于最大化，即FRFFBB越接近于Fopt=V1時，R最大。由以上分析可知，最大化頻譜效率等效于混合預編碼矩陣與最優預編碼矩陣間歐式距離最小的，即：

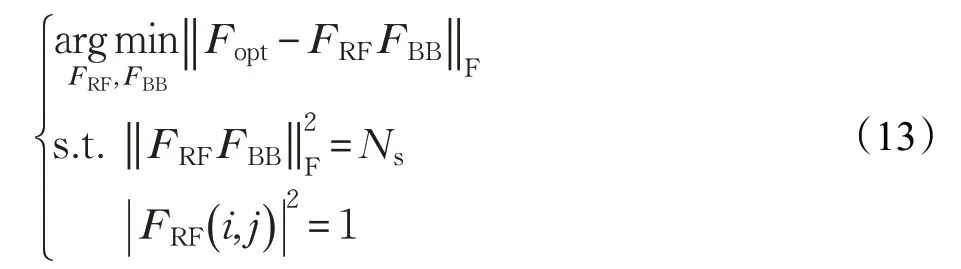
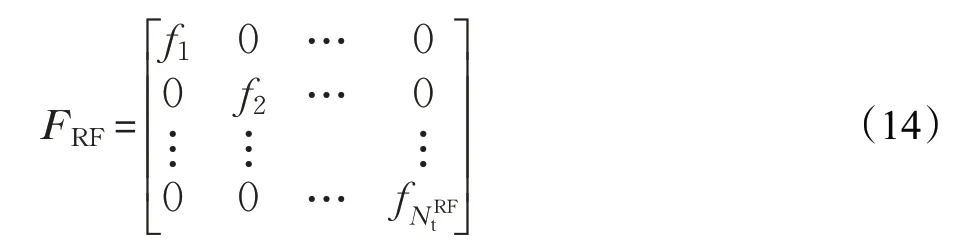
式中，FRF的維度為中每一塊向量為fi=j=1,2,…,Nt為第j個相移器的相位。

3 混合預編碼設計

考慮單用戶傳輸場景，本文采用部分連接結構，證明了信道矩陣H的有序右奇異值向量角度可以作為初始化模擬預編碼矩陣，不需要發射機處的天線陣列響應矢量。

3.1 初始化模擬預編碼器設計

根據文獻[9]和[13]中分析，混合預編碼優化問題可以重寫為：

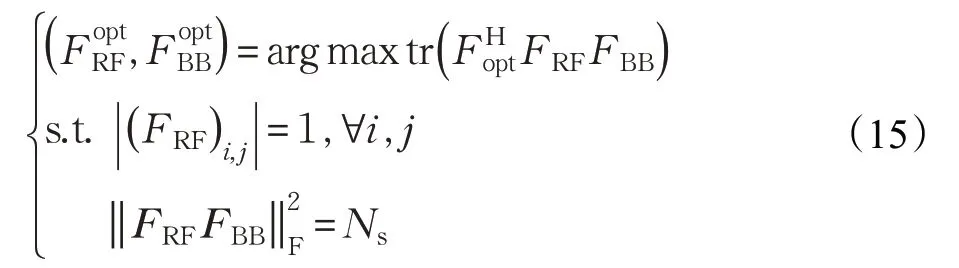
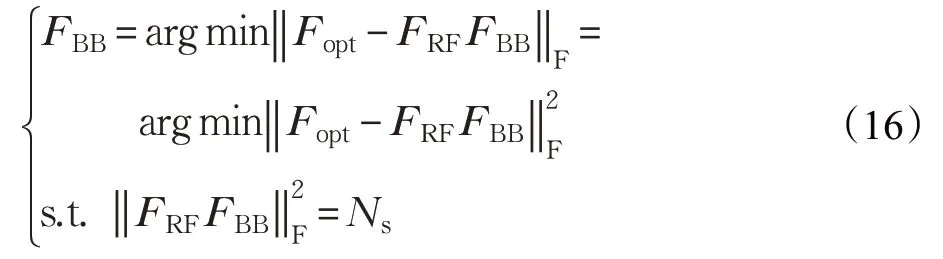
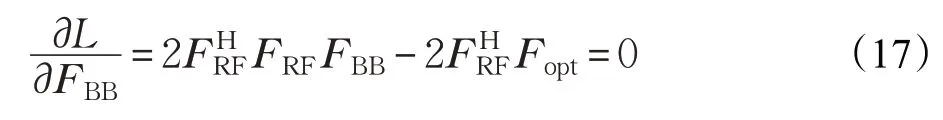
由式（17）可得：

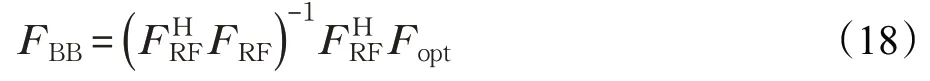
將式（11）代入式（10）中得到：

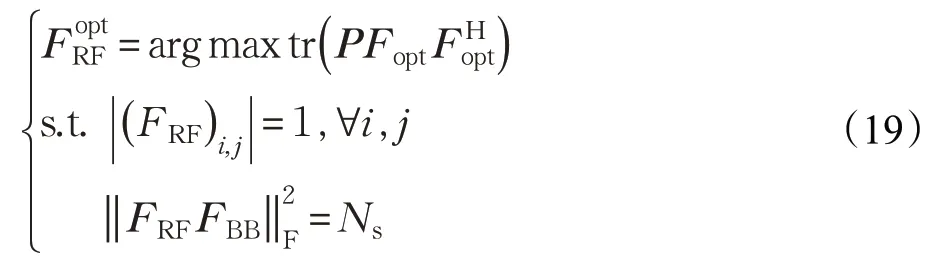
命題1給定矢量，集合F={f∈ ?N×1:|f(n)|=1,?n} ，對任意f∈F，有：

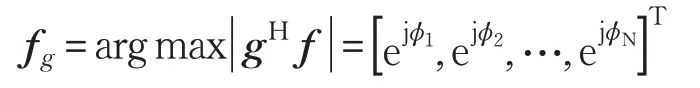
證明設，則有：

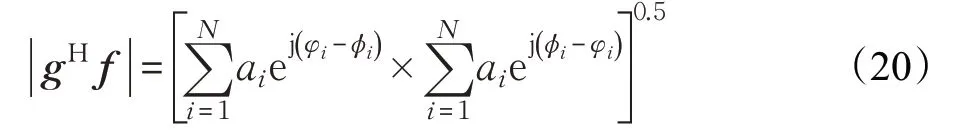
根據命題1可知，要使SRF和Sopt內積最大，則FRF和Fopt構成的子空間相同，已知Fopt為信道矩陣右奇異值矩陣，對應相位角度構成其子空間，由于單模限制，則FRF可取信道右奇異值矩陣元素對應的相位角度構成。

通過以上分析可知，可用信道矩陣右奇異值矩陣元素的相位角度初始化模擬預編碼器。具體初始化過程即：

式中，U為Nr×Nr維酉矩陣，V為Nt×Nt維酉矩陣，Σ是對角矩陣，且對角元素按降序排列。設φm,n為V的第m行和第n列元素的相位角度，取V中元素的相位角度作為集合F，即：

也即取F 集的前NRF列矢量。應用到式（14）中，進行塊對角化，則最終得到的初始模擬預編碼矩陣為：

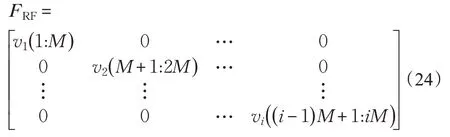
式中，vi((i-1)M+1:iM)表示取vi中第(i-1)M+1 至iM個元素。

3.2 應用交替迭代結構設計

獲取初始化模擬預編碼器FRF后，應用交替最小化結構，固定FRF，根據最小化Fopt和FRFFBB的歐氏距離，優化FBB，?。?/p>

4.1 實驗仿真分析

本文仿真基于部分連接結構下毫米波MIMO系統，其中毫米波信道路徑數L=10 ，ULA 的天線間距為d=λ/2，假設到達和離開方位角在[0,2 π]上均勻分布。本節給出了在低信噪比和高信噪比下以及不同射頻鏈路下Alt-ISVD 算法的頻譜效率的仿真曲線，并仿真了不同射頻鏈路下Alt-ISVD 算法的能效。實驗仿真中，發射天線數目為Nt=128，接收天線數目為Nr=16 或Nr=32。

在收發端天線配置為Nt×Nr=128×16 且發送端射頻鏈4，數據流數為Ns=4，低信噪比下不同算法的頻譜效率隨信噪比變化曲線如圖2所示，可以看出，本文Alt-ISVD算法性能優于文獻[13]提出的Alt-SDR算法和文獻[15]提出的算法1，且隨著信噪比增大，差異越明顯。隨著信噪比增大，本文所提算法性能越來越接近文獻[15]提出的算法2，但復雜度低于文獻[15]提出的算法1和算法2。

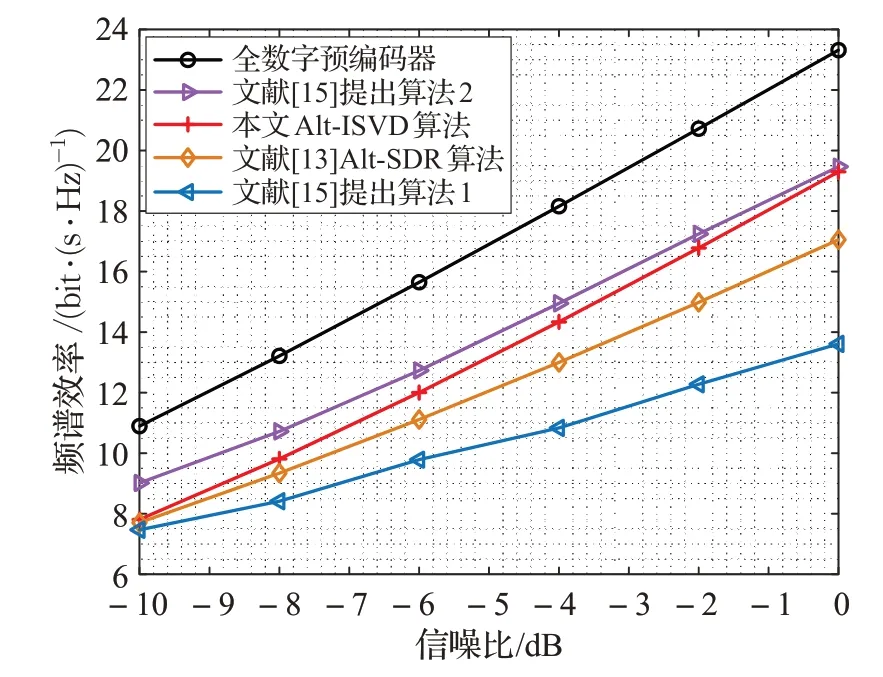
圖2 低信噪比下，Nt×Nr=128×16 且=Ns=4時的系統性能

圖3 所示為Nt×Nr=128×16 且s=4 時，高信噪比下，不同算法的頻譜效率隨信噪比增加的曲線，由圖可知，在高信噪比下，本文所提Alt-ISVD 算法明顯優于文獻[13]Alt-SDR算法和文獻[15]提出的算法1。當信噪比約大于5 dB 時，Alt-ISVD 算法的頻譜效率高出文獻[15]提出的算法2，并且隨著信噪比增加，性能越優于文獻[15]提出的算法2。

圖4 所示為SNR=0 ，Nt×Nr=128×32 且Ns=2時，不同射頻鏈路數目下，本文Alt-ISVD 算法、全連接OMP 算法、全數字預編碼器和文獻[13]Alt-SDR 算法頻譜效率曲線。由圖可知，本文Alt-ISVD 算法與全連接OMP算法相比，性能略低，這是由于使用較少的相移器帶來的性能損失，但本文Alt-ISVD算法性能高于文獻[13]Alt-SDR算法。

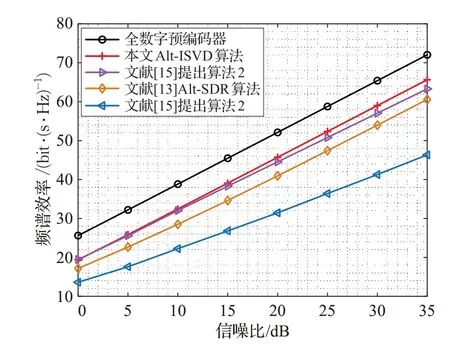
圖3 高信噪比下，Nt×Nr=128×16 且=Ns=4時的系統性能

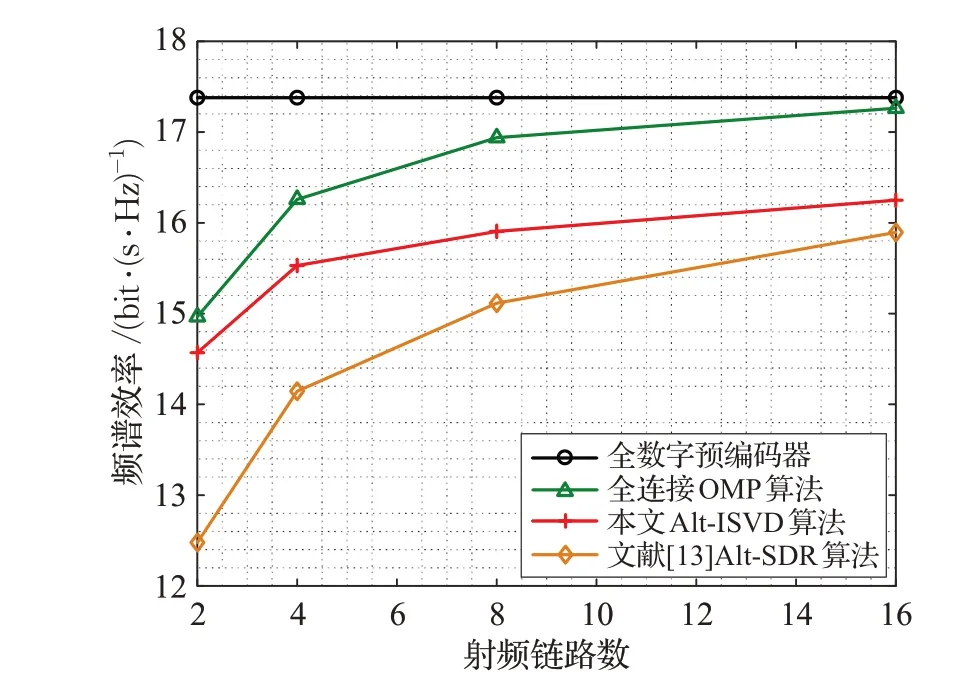
圖4 SNR=0,Nt×Nr=128×32 且 N s=2時，不同射頻鏈數的系統性能

本文還仿真了不同數目下，Alt-ISVD 算法、全連接OMP算法、文獻[13]Alt-SDR算法的能源效率，仿真參數設置為：Pco=10 W，PRF=100 mW，PPA=100 mW 和PPS=10 mW[13]。根據文獻[13]，能效計算公式為：

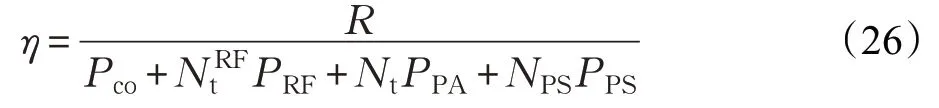
式中，Pco為發送端公共功率，PRF,PPA和PPS分別為每條RF鏈，功率放大器和移相器的功率。其中，全連接移相器個數為，部分連接移相器個數為NPS=Nt。

圖5所示為SNR=0,Nt×Nr=128×32 且Ns=2 時，不同射頻鏈路數目下，本文Alt-ISVD算法、全連接OMP算法、文獻[13]Alt-SDR算法能源效率曲線。由圖可知，本文所提Alt-ISVD算法的能效高于全連接OMP算法和文獻[13]Alt-SDR 算法，且隨著RF 鏈數增加，本文Alt-ISVD算法與OMP算法的能源效率比值越高，這是因為隨著RF 鏈數增加，全連接OMP 算法的移相器增加，大大增加了功耗。

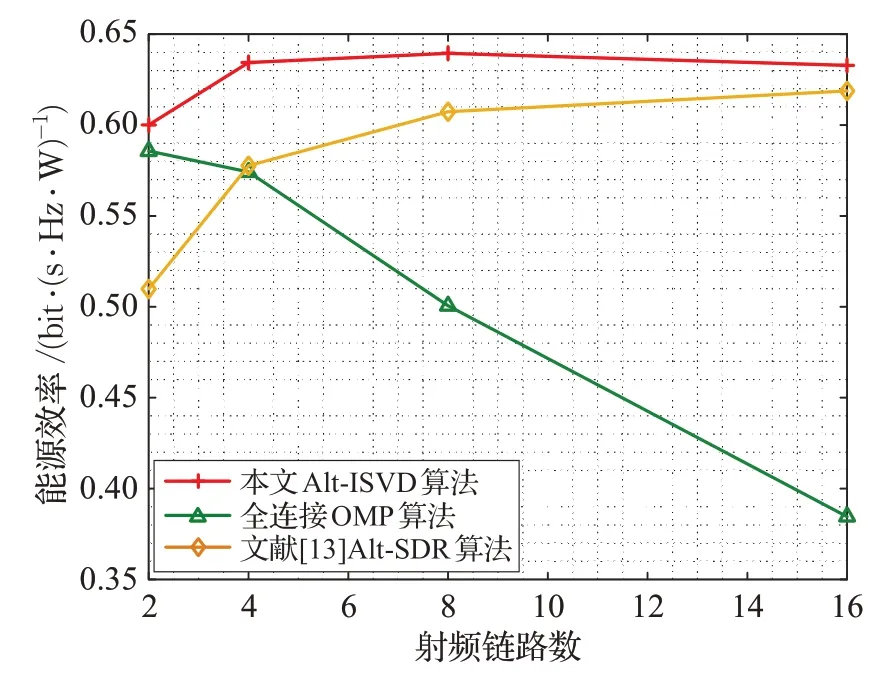
圖5 SNR=0,Nt×Nr=128×32 且 N s=2時，不同射頻鏈數的能源效率

4.2 算法復雜度分析

文獻[15]的算法和提出的Alt-ISVD 算法復雜度如表1 所示。本文所提算法利用信道右奇異值矩陣的前列來初始化模擬預編碼器，根據截短SVD（Truncated SVD，TSVD）[16]，復雜度為，獲取最優數字預編碼器復雜度為，每次迭代更新數字預編碼器復雜度為每次迭代更新模擬預編碼器復雜度為文獻[15]算法1 中，初始化復雜度為，每次迭代復雜度為，其中rH=rank(H)，利用注水算法求數字預編碼器復雜度為在文獻[15]算法2 中，每次迭代獲取模擬預編碼器的復雜度為，數字預編碼器通過注水得到，算法復雜度為在實際傳輸系統中，Ns≤NRF?M ＜Nr＜Nt，可以得出，本文所提Alt-ISVD算法復雜度比文獻[15]更低。

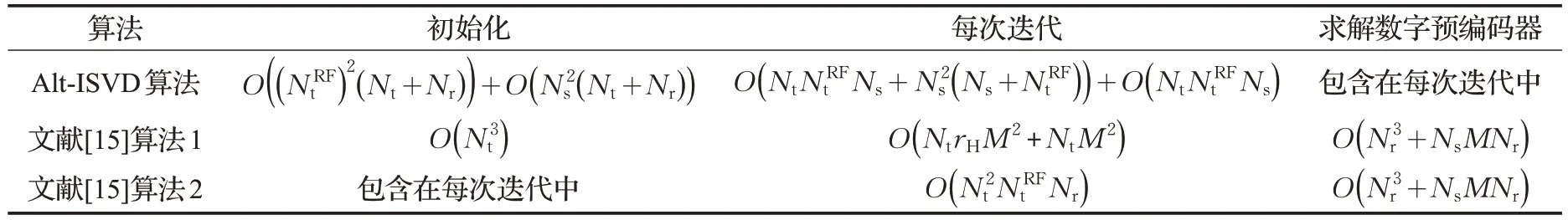
表1 文獻[15]算法和Alt-ISVD復雜度

5 結束語

考慮實際工程應用，全連接型混合預編碼能耗太高。文章研究了毫米波MIMO 系統中部分連接型混合預編碼，證明了初始化模擬預編碼器可由信道右奇異值向量的相位角度導出，可以避免采用搜索近似最佳模擬預編碼矩陣的復雜優化過程且不需要知道發射天線陣列響應矢量，降低了復雜度，最后交替應用最小化結構提升性能。仿真結果表明，隨著信噪比的增高，本文所提算法性能高于文獻[15]提出的算法，且復雜度更低。與傳統OMP 算法相比，本文所提算法擁有更高的能源效率，降低了硬件功耗，更貼切實際應用。