基于擴(kuò)展卡爾曼濾波算法的二階電池模型SOC估算

查偉民

(方大新材料(江西)有限公司，江西 南昌 330096)

電池管理系統(tǒng)是電動(dòng)汽車(chē)的關(guān)鍵部件之一，具有電池系統(tǒng)狀態(tài)監(jiān)測(cè)、故障診斷與保護(hù)、均衡管理和絕緣檢測(cè)等功能。對(duì)電池組中單體電池的SOC進(jìn)行精確地估算，可以為電池管理系統(tǒng)進(jìn)行能量均衡提供依據(jù)與判斷，有利于延長(zhǎng)電池的使用壽命[1]。

目前常用的SOC 估算方法有開(kāi)路電壓法、安時(shí)積分法、神經(jīng)網(wǎng)絡(luò)法和卡爾曼濾波算法等[2]。開(kāi)路電壓法需要長(zhǎng)時(shí)間靜止測(cè)得電池兩端開(kāi)路電壓(OCV)，再通過(guò)查表形式或者多項(xiàng)式形式確定對(duì)應(yīng)的SOC值。安時(shí)積分法可以精確地估算電池的SOC，但是此方法需要精確的初始SOC值，不能避免錯(cuò)誤的初始SOC所帶來(lái)的誤差。神經(jīng)網(wǎng)絡(luò)算法需要大量的歷史試驗(yàn)數(shù)據(jù)來(lái)進(jìn)行訓(xùn)練與預(yù)測(cè)，該方法計(jì)算量十分龐大，在計(jì)算能力差的硬件上很難應(yīng)用[3-6]。國(guó)內(nèi)外利用卡爾曼濾波算法對(duì)電池SOC估算方面進(jìn)行了大量的研究，主要有擴(kuò)展卡爾曼濾波算法和無(wú)跡卡爾曼濾波算法等。本文主要運(yùn)用MATLAB/Simulink平臺(tái)對(duì)電池的二階模型進(jìn)行了建模，運(yùn)用MATLAB工具箱中的最小二乘法對(duì)電池模型參數(shù)進(jìn)行了辨識(shí)，然后再利用擴(kuò)展法卡爾曼濾波進(jìn)行SOC估算，并對(duì)結(jié)果進(jìn)行了分析與討論。

1 電池等效電路模型

電池等效電路模型主要有PNGV模型、Thevenin 模型、二階RC 等效電路模型以及N階RC等效電路模型等。一般情況下隨著RC個(gè)數(shù)增加，模型就越精確；但是隨著RC個(gè)數(shù)增加，所需要辨識(shí)的模型參數(shù)也就越多，相應(yīng)的計(jì)算量也會(huì)增大[7-10]。為平衡模型精度和計(jì)算量，本文選取二階RC模型作為電池模型來(lái)進(jìn)行仿真與估算，如圖1所示。

圖1 二階等效電池模型

電池的剩余電量估計(jì)是電池管理系統(tǒng)的關(guān)鍵技術(shù)之一，其能夠直觀的反映電池的荷電狀態(tài)。美國(guó)先進(jìn)聯(lián)合會(huì)(USABC)從電量角度將電池荷電狀態(tài)SOC定義為：在一定放電條件(恒流、恒溫)下，電池剩余容量與相同條件下額定容量的比值。

(1)

式中：SOC(t)表示t時(shí)刻的SOC值，SOC(t0)表示t0時(shí)刻的SOC值，η表示庫(kù)倫效率，這里η=1，I表示輸入的電流，Qn表示電池額定容量。根據(jù)電路的基爾霍夫定律可知，二階模型可以由式(2)來(lái)表示：

(2)

式中：R0為電池模型歐姆內(nèi)阻，R1和R2為電池模型極化內(nèi)阻，C1和C2為電池模型極化電容，U1和U2分別為R1和R2兩邊的電壓，Ut為電池的端電壓，Uoc為電池的開(kāi)路電壓，It為流過(guò)電池的電流。

2 電池模型的參數(shù)辨識(shí)

在進(jìn)行仿真與估算之前，需要對(duì)二階RC等效電路模型進(jìn)行參數(shù)辨識(shí)，本文主要運(yùn)用離線辨識(shí)的方法對(duì)二階模型進(jìn)行參數(shù)辨識(shí)。首先對(duì)電池進(jìn)行混合脈沖功率特性工況(HPPC)放電實(shí)驗(yàn)，實(shí)驗(yàn)電池為NCR18650電池，脈沖電壓曲線如圖2(a)所示。現(xiàn)選取單個(gè)脈沖對(duì)電池模型進(jìn)行參數(shù)辨識(shí)，如圖(b)所示。電壓從A點(diǎn)到B點(diǎn)的突然下降主要是由電池歐姆內(nèi)阻所引起的，電壓從B點(diǎn)到C點(diǎn)主要是由極化電容的遲滯效應(yīng)所引起的，當(dāng)電流突然卸載之后，由于歐姆內(nèi)阻的作用，由C點(diǎn)瞬間上升到D，然后再由D點(diǎn)緩慢上升，直至平穩(wěn)。

(a)采集的電壓曲線

這一過(guò)程中歐姆內(nèi)阻R0可由式(3)表示：

(3)

式中：R0為電池歐姆內(nèi)阻，I為輸入電流。

從C點(diǎn)到D點(diǎn)直至平穩(wěn)過(guò)程中，電池端電壓可以表示為：

V=VOC-V1(0)e-t/R1C1-V2(0)e-t/R2C2

(4)

式中：V1為電路模型中R1C1端的電壓，V2為電路模型中R2C2端的電壓。

由A點(diǎn)到C點(diǎn)過(guò)程中，電池端電壓可以表示為：

V=VOC-IR0-IR1(0)e-t/R1C1-IR2(0)e-t/R2C2

(5)

在C點(diǎn)處，RC并聯(lián)網(wǎng)絡(luò)的電壓等于式(4)中的初始電壓，即

(6)

根據(jù)式(4)、(5)和(6)，利用MATLAB的cftool工具箱[11]，辨識(shí)出二階模型的各個(gè)參數(shù)，見(jiàn)表1。

表1 放電過(guò)程中模型離線參數(shù)辨識(shí)結(jié)果

在單個(gè)HPPC脈沖放電工況中，放電完成后經(jīng)過(guò)長(zhǎng)時(shí)間靜止，可以將此時(shí)的電壓作為電池OCV，因此記錄每次脈沖放電后的SOC值與其對(duì)應(yīng)的OCV值，兩者的關(guān)系可以由六次多項(xiàng)式來(lái)表示，擬合曲線如圖3所示。

圖3 OCV-SOC擬合曲線圖

電池的SOC-OCV關(guān)系可以由式(7)來(lái)表示：

Uoc=19.068SOC6-56.276SOC5+

60.844SOC4-28.32SOC3+4.766SOC2+

0.809SOC+3.288

(7)

3 擴(kuò)展卡爾曼濾波算法的SOC估算

擴(kuò)展卡爾曼濾波算法和無(wú)跡卡爾曼濾波算法都能對(duì)非線性系統(tǒng)進(jìn)行最優(yōu)狀態(tài)估計(jì)，本文只利用擴(kuò)展卡爾曼濾波算法進(jìn)行電池的SOC估算。擴(kuò)展卡爾曼濾波的基本思想是利用泰勒公式在狀態(tài)估計(jì)值處對(duì)非線性系統(tǒng)進(jìn)行一階泰勒展開(kāi)，將系統(tǒng)線性化，然后運(yùn)用卡爾曼濾波算法對(duì)系統(tǒng)狀態(tài)進(jìn)行估算。

根據(jù)式(2)可以將電池模型狀態(tài)方程和觀測(cè)方程轉(zhuǎn)化為：

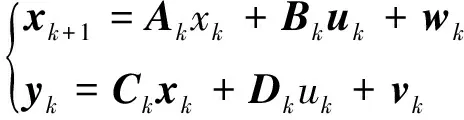
(8)

式中:wk為過(guò)程噪聲，其均值為零，方差為Q的高斯白噪聲，vk為觀測(cè)噪聲，也是均值為零，方差為R的高斯白噪聲，ΔT為采樣時(shí)間，這里為1 s。

Ck=[-1-1dUoc(SOC)/d(SOC)]Dk=-R0

xk=[U1(k)U2(k)SOC(k)]

uk=I(k)

卡爾曼濾波算法的步驟如下：

(9)

(2)狀態(tài)預(yù)測(cè)

(10)

(3)協(xié)方差預(yù)測(cè)

(11)

(4)計(jì)算卡爾曼增益

(12)

(13)

(6)更新?tīng)顟B(tài)

(14)

(7)協(xié)方差矩陣

(15)

4 仿真結(jié)果與分析

通過(guò)MATLAB/Simulink平臺(tái)建立電池二階等效模型，并利用擴(kuò)展卡爾曼濾波算法對(duì)電池SOC進(jìn)行估算。實(shí)際電池測(cè)試中，先將電池充滿電，因此實(shí)際中的SOC為1，參考SOC值可以用安時(shí)積分法在無(wú)噪聲的情況下來(lái)計(jì)算，可視為理想SOC值。圖4為EKF算法流程圖。在HPPC工況下，實(shí)際的SOC值與EKF估算SOC值及誤差值如圖5(a)和(b)所示，從圖上可以看出，EKF算法估算的SOC與實(shí)際值誤差不大，很好的追蹤了實(shí)際的SOC值，通過(guò)計(jì)算可得，最大絕對(duì)誤差值為0.019 8，平均絕對(duì)誤差值為0.006 4，平方根絕對(duì)誤差值為0.08。實(shí)際測(cè)量的電壓值與EKF估算的電壓值及誤差值如圖6(a)和(b)所示，從圖中可以看出實(shí)際測(cè)量的電壓值與EKF估算的電壓值相吻合，其最大絕對(duì)誤差值為0.059 8 V，平均絕對(duì)誤差值為0.002 V，平方根絕對(duì)誤差值為0.045 V。

圖4 EKF算法流程圖

(a)EKF算法估算SOC曲線

(a)EKF算法電壓預(yù)測(cè)曲線

為檢驗(yàn)EKF算法在電池SOC估算方面是否具有魯棒性，現(xiàn)將初始的SOC值假設(shè)為0.9，然后再利用EKF算法對(duì)HPPC工況進(jìn)行仿真與分析。SOC估算結(jié)果如圖7(a)和(b)所示,從圖中可以看出，即使初始SOC值不確定的情況下，EKF算法也能夠很好的追蹤實(shí)際的SOC值，以誤差為0.05為基準(zhǔn)點(diǎn)，EKF算法將在351 s時(shí)得到收斂，通過(guò)計(jì)算得知平均絕對(duì)值誤差為0.007 3，均方根絕對(duì)誤差為0.085 3。電壓估算曲線如圖8(a)和(b)所示，從圖中可以看出，電壓估算曲線在SOC初始值不確定的情況下也能很好的追蹤實(shí)際的電壓曲線，其平均絕對(duì)誤差值為0.003 2 V，平方根絕對(duì)誤差值為0.057 V。

(a)EKF算法估算SOC曲線

(a)EKF算法電壓預(yù)測(cè)曲線

5 結(jié)束語(yǔ)

本文以鋰離子單體電池為實(shí)驗(yàn)對(duì)象，進(jìn)行了HPPC工況脈沖放電實(shí)驗(yàn)，再通過(guò)MATLAB/Simulink仿真平臺(tái)對(duì)其進(jìn)行了等效電路模型的建模，并通過(guò)最小二乘法參數(shù)辨識(shí)原理對(duì)二階模型的各個(gè)參數(shù)進(jìn)行了離線參數(shù)辨識(shí)，最后利用擴(kuò)展卡爾曼濾波算法對(duì)電池等效電路模型進(jìn)行了SOC與電壓估算。在準(zhǔn)確初始值和假設(shè)初始值兩種情況下進(jìn)行仿真驗(yàn)證，單體電池的SOC誤差在0.01以內(nèi)，電壓估算誤差在0.005 V以內(nèi)。在初始值不確定的情況下，電池SOC曲線與估算電壓曲線也能夠快速收斂于真實(shí)值，這表明EKF算法在電池SOC估算方面具有精度高、收斂快和實(shí)用性較強(qiáng)的優(yōu)點(diǎn)。未來(lái)的工作中，電池健康狀況將成為主要研究方向。該算法還需進(jìn)行硬件在環(huán)測(cè)試，以驗(yàn)證其在實(shí)際工作中的效果。