利用Z比分數分析試驗間質量控制數據

曹文婷

(貴州省質安交通工程監控檢測中心有限責任公司，貴州 貴陽 550000)

0 引 言

利用數理穩健統計法處理實驗室給出的結果，并分析參加實驗室的檢測技術能力狀況。采用Z比分數的結果來進行分析和判斷。如顯示結果異常，即判定其結果為不滿意(或有問題)。

1 研究背景

本文基于某次作為發起實驗室，組織的實驗室間比對，對標志反光膜逆反射系數測定9對角的測試得出9個水平的分析數據，再通過Z比分數對實驗室提交的數據進行分析，可以比較實驗室之間的數據，強調實驗室間的能力的差，是目前實驗室間能力驗證通用的統計方法。一般來說本統計技術能夠較好地反映樣品分析的總體狀況。通過能力驗證活動，參加實驗室可以了解分析項目的整體水平和自已所處的位置，有利于找到差距，進一步分析原因，從而提高自身技術能力和管理水平。

2 統計概述

本主要對該次能力驗證計劃的穩健統計參數、參加實驗室的總體能力狀況、各參加實驗室的能力比分數等進行了統計。統計穩健變異系數介于4.8%～10.3%之間，穩健變異系數是表示結果變異性的一個參數，由此可見參加該次能力驗證實驗室在9對角的整體分析水平較高。主要穩健參數的統計結果如表1所示。

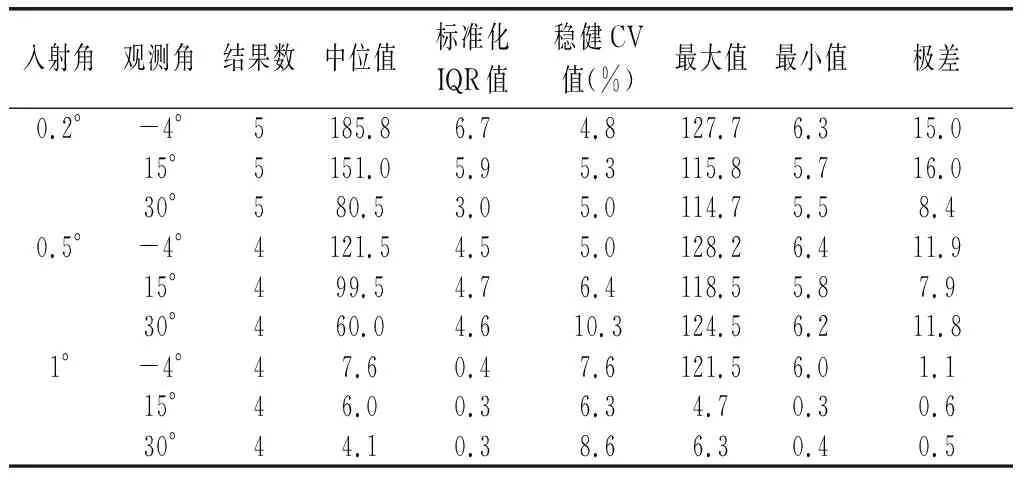
表1 主要穩健統計參數匯總表

3 格拉布斯離群檢測

GB/T 4883-2008《數據統計處理和解釋 正態樣本離群值的判斷和處理》中提到用樣本中位值、標準差、最大最小觀察值計算統計量Gn、Gn’，根據格拉布斯臨界值判定樣本的離群情況。

4 四分位穩健統計技術

該方法可以降低極端值(即離群值)對統計結果的影響，它對極端值的處理方式是盡可能降低其權重，而不是將其從數據組中完全剔除，使平均值估計值和標準差估計值被影響程度降至最小。該方法與經典統計方法相比在極端值的影響方面較為優越。其使用中位值、IQR值代替了傳統的平均值、標準偏差，用穩健Z比分數代替經典Z比分數來評定參加能力驗證的實驗室的檢測能力。

5 主要穩健統計參數

該次能力驗證計劃采用同一樣品檢測、四分位穩健統計技術，主要統計參數為：結果數量(N)、中位值(M)、標準四分位間距(NIQR)、上四分位值(Q3)、下四分位值(Q1)、穩健變異系數(CV)、最小值(MIN)、最大值(MAX)、極差(R)。其中最主要的統計參數是中位值和IQR，因為它們是穩健的統計量，較少受數據中存在的離群值的影響。各統計參數的數學含義與計算方法如下：

結果數量(N)：參加能力驗證實驗室按照作業指導書要求報告的有效檢測結果數目。

中位值(M)：是一組數據的中間值，它是全部觀察結果按大小順序排列位次居中的那個數值。在全部觀察值中，有一半的數值比它大，有一半的數值比它小。如果N為奇數，中位值是一個單一的中心值，為X(n+1)/2，[X(n/2)+X(n/2)+1]/2

四分位數間距(IQR)：是指上四分位數與下四分位數之差，其間包括了全部觀察值的一半，其數值越大，說明分散程度愈大；反之，說明分散程度愈小。

上四分位值(Q3)：是指全部觀察值中有四分之一的觀察值比它大的一個值，為(3n/4+1/4)次序的觀察值；

下四分位值(Q1)：是指全部觀察值中有四分之一的觀察值比它小的一個值，為(n/4+3/4)次序的觀察值。

若一組觀察值X1、X2，……XN，N為觀察值的個數。按序以小到大排列該觀察值為X{1}，X{2}，……X{N}，設A=1/4(N-1)、B=3/4(N-1)，則下四分位值Q1=(Q中+1)/2、上四分位值Q3=Q中+Q1-1

標準化四分位數間距(NIQR)：四分位數間距(IQR)乘以系數0.741 3，相當于一個標準差。

穩健變異系數(CV)：標準化四分位間距除以中位值，并以百分數表示，相當于經典的變異系數(標準差除以均值)。

穩健分析由穩健估計平均值、標準差迭代計算得出新的估計穩健平均值、標準差，直至過程收斂。當穩健標準差的第三位有效數字和穩健平均值相對應的數字在連續兩次迭代中不再變化時，即可認為過程是收斂的。

四分位數間距(IQR)=上四分位值(Q3)-下四分位值(Q1)

標準化四分位數間距(NIQR)=IQR×0.741 3

穩健Z值等于觀察值與中位值的差再除以NIQR。

注：因子0.741 3由標準正態分布得到。標準正態分布時均數為零，標準差為1，而這時四分位數間距是[-0.674 5，+0.674 5]，其寬度為1.349 0，故四分位數間距乘以(即0.741 3)相當于標準偏差。

實驗室檢測結果評價標準

利用Z比分數對參加實驗室的能力進行判定，判定的標準分為3種情況：

①︱Z︱≦2為滿意結果；

②2﹤︱Z︱﹤3為有問題的結果(可疑值)；

③︱Z︱≥3為不滿意結果(離群值)。

6 結 語

該次能力驗證活動為了能準確了解參加實驗室日常分析的實際能力狀況，對測試方法作了統一要求，各實驗室均采用規定檢測方法進行測試。反饋檢測結果顯示通過格拉布斯進行離群檢測以及Z比分數穩健統計分析，顯示各家測量結果無離群情況，并且比對結果均為“滿意”，具體情況如表2所示。

表2 Z比分數結果