系統振蕩時對距離保護阻抗特性比較研究

郭楊，王煜，周永榮，陳昊

（1.國網江蘇省電力有限公司檢修分公司，江蘇 南京 211102；2.國網電力科學研究院有限公司，江蘇 南京 211106）

0 前言

在電力系統中，當出現輸電線路輸送功率超過極限值造成靜態穩定破壞，或者電網發生短路故障，切除大容量的發電、輸電或變電設備，負荷瞬間發生較大突變等造成電力系統暫態穩定破壞時，都將引起電力系統振蕩[1-2]。作為一種常見的非正常運行狀態，發生振蕩后系統可以繼續運行，保護不必動作，只需根據預先的解列點判別系統是否解列運行即可。

距離保護能夠反應輸電線路一側電氣量變化，具有穩定性好、靈敏度高等優點，能夠滿足復雜的網絡迅速、有選擇性地切除故障，在輸電線路保護中具有廣泛應用[3-4]。但是，電力系統振蕩對電網距離保護的影響一直是個無法規避的現實問題。對于距離保護，測量阻抗的幅值與相角都會發生周期性的變化，當測量阻抗進入保護的動作區時，保護就會動作。目前，對系統振蕩時的距離保護已有較多研究。文獻[5]提出了在微機距離保護中加入振蕩閉鎖裝置；文獻[6]從美國“8·14”大停電事故出發，論述了電力系統振蕩對距離保護的影響及其閉鎖；文獻[7] 提出了一些系統振蕩時距離保護的對策；文獻[8]分析了多相補償距離繼電器在振蕩且伴隨單相接地故障下的動作性能。上述文獻多研究了系統振蕩時距離保護的閉鎖問題，但是對于振蕩過程中，不同動作特性阻抗繼電器造成繼電器本身動作這一課題尚未研究。

本文具體分析了系統振蕩時，保護安裝處測量阻抗的變化規律。以此為基礎，通過計算測量阻抗進入保護動作區的時間，并輔以圖形化的直觀方式分析了阻抗繼電器不同動作特性曲線受系統振蕩影響而造成繼電器動作的情況。

1 系統振蕩的概念

并聯運行的電力系統或發電廠之間出現功率角大范圍周期性變化的現象，稱為電力系統振蕩。電力系統正常運行時，接入系統的所有發電機都處于同步運行狀態。因輸電線路傳輸功率過大超過靜態穩定極限、系統無功嚴重不足、發生故障后切除太慢和采用非同步重合閘時，并列運行的發電機會失去同步，系統發生振蕩。當電力系統中發生振蕩時，各點的電壓、電流和功率的幅值和相位都將發生周期性地變化。電壓與電流之比所代表的阻抗繼電器的測量阻抗也將周期性地變化，當測量阻抗進入動作區域的時間大于動作定值，距離保護將可能發生動作。因此對于距離保護必須考慮電力系統振蕩對其的影響[9]。

2 振蕩對距離保護測量元件的影響

2.1 系統振蕩時電流電壓的變化規律

以下圖所示的雙側電源的電力系統為例，分析系統振蕩時電流電壓的變化規律。設系統兩側電動勢分別為EM和EN，相角差為δ，電源之間的阻抗ZΣ為ZM、ZL、ZN三者之和。其中，ZM為M 側系統的等值阻抗，ZN為N 側系統的等值阻抗，ZL為聯絡線路的等值阻抗[10]。

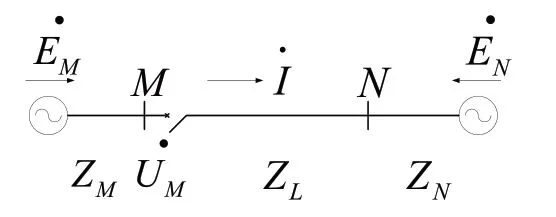
圖1 雙端電源系統接線圖

2.2 系統振蕩時測量阻抗的規律

當系統振蕩時，安裝在M 點處的測量元件的測量阻抗為[11]：

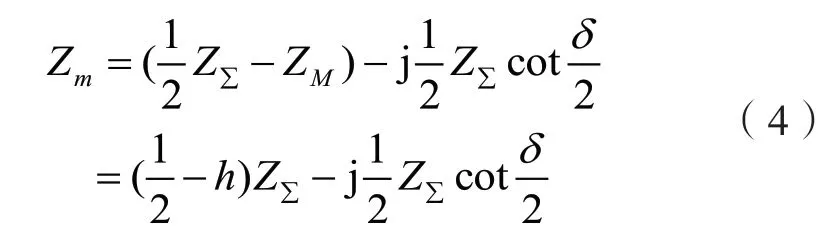
式中，h=ZM/Z∑為M 側系統阻抗占系統總聯系阻抗的比例。當h=1/2 時，振蕩軌跡經過原點，即振蕩安裝處就是振蕩中心；當h＜1/2 時，振蕩軌跡經過+jX 軸，振蕩中心在保護正方向；當h＞1/2 時，振蕩軌跡經過-jX 軸，振蕩中心在保護反方向。

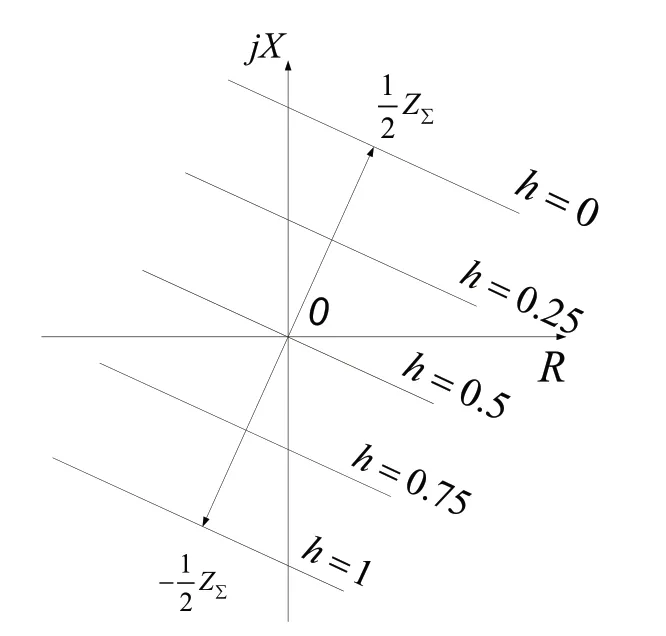
圖2 不同距離保護安裝地點處測量阻抗的變化

一般而言，h＜1/2，即振蕩中心在保護的正方向。當系統振蕩時，保護安裝處M 的測量阻抗由兩大部分組成，第一部分為（1/2-h）ZΣ，對應從保護安裝處M 到振蕩中心的線路阻抗，只與保護安裝點M 到振蕩中心的相對位置有關，與功角δ 無關。第二部分為 -j ZΣcot(δ/2)/2 ，垂直于第一部分，隨著功角的變化而變化。當功角δ 從0°變化到360°時，測量阻抗的末端沿著一條經過振蕩中心且垂直于Z 的直線OO’自右向左移動。當δ=0° (+) 時，測量阻抗Zm位于復平面右側，其值無窮大；當δ=180°時，測量阻抗Zm值最小，為（1/2-h）ZΣ，與系統阻抗角同方向；當δ=360°(-)時，測量阻抗值也為無窮大，但是位于復平面的左側。

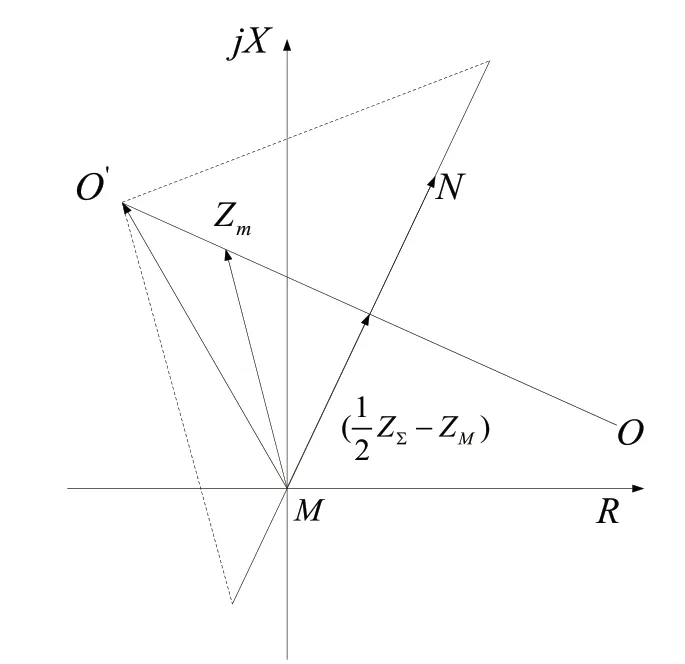
圖3 系統振蕩時測量阻抗的變化

當EM與EN的幅值不相等時，測量阻抗的變化曲線將發生變化。設EN/EM=k，代入式（4）可得：

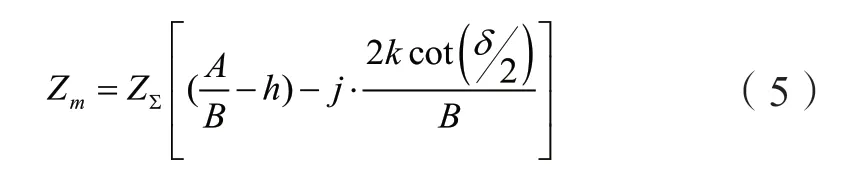
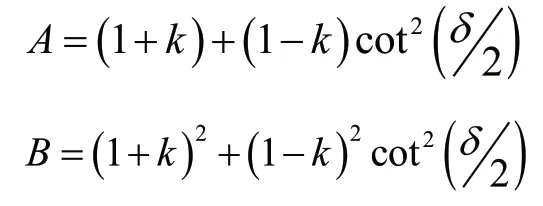
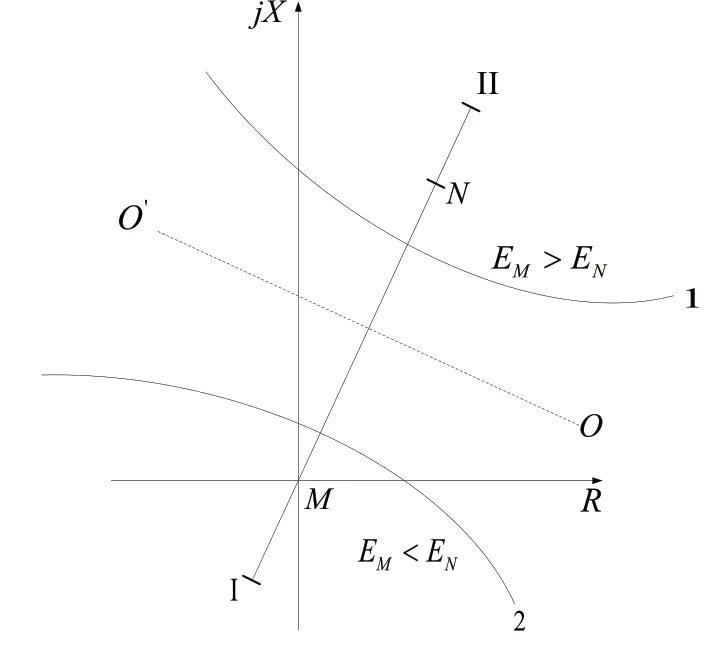
圖4 兩側電源不等值時的測量阻抗曲線

從圖4 可以看出，系統振蕩時測量阻抗末端的軌跡將不再是一條直線，而是一段圓弧。同時，根據以上推導，可以分析系統振蕩時距離保護所受到的影響。

2.3 阻抗繼電器造成保護動作的分析

據文獻[12] 可知，電力系統的振蕩周期為1.5 s ～2.0 s。在系統失去穩定后，第一個振蕩周期較長；當振蕩發展起來后，振蕩周期則縮短；在最后拉入同步時，振蕩周期又會增加。對于無延時特性的Ⅰ段速斷保護而言，只要保證振蕩中心不落入本線路保護范圍內，振蕩對保護將不造成影響；對于限時速斷特性的Ⅱ段保護而言，只要振蕩中心不落入本線路及相鄰線路的保護范圍內，或者動作時間大于測量阻抗落入保護范圍內的時間，就不會動作[13]；對于具有定時限特性的Ⅲ段保護而言，只要動作時間大于2.0 s，保護一般不會動作。從理論分析來看，由于距離Ⅱ段保護的動作時間處于可能動作的范圍，且實際運行中距離Ⅱ段整定較為富于變化，對Ⅱ段保護的動作特性分析具有很強的針對性和實際意義[14]。本文經理論推導可知，相對于圓特性阻抗繼電器，四邊形阻抗繼電器具有更強的穩定性，在系統振蕩時能有效防止繼電器動作，并通過仿真分析驗證了結論的正確性。

3 仿真分析

本文的仿真分析中，以某500 kV 輸電線路為例，線路及兩側的等值阻抗如圖5 所示。圖中M 處安裝的距離保護，按距離保護Ⅱ段值整定，具體定值如表1 所示。

圖5 某500 kV輸電線路及兩側等值阻抗

該線路配備兩套保護裝置，分別是南瑞繼保RCS-931 保護和四方繼保CSC-103A 保護。對于線路的兩套后備距離保護，RCS-931 保護采用圓特性阻抗繼電器，CSC-103 保護采用四邊形特性阻抗繼電器。距離Ⅱ段保護動作時間整定為0.7 s[15]。從圖6 可以看出，不同比值k情況下的測量阻抗變化曲線經過保護范圍的情況。在圖6 中，有圓特性阻抗繼電器和四邊形特性阻抗繼電器兩種距離保護裝置，兩邊電源電動勢幅值的比值EN：EM=k從0.6～1.6 遞增，對應圖中的6 條測量阻抗變化曲線。由圖可知，在相似整定值的條件下，測量阻抗經過圓特性曲線的時間明顯大于經過四邊形特性曲線的時間。因此，方向圓阻抗繼電器受振蕩的影響大于四邊形阻抗繼電器所受的影響。采用圓特性曲線的阻抗繼電器在系統振蕩時，更容易動作。因此，繼電器的動作特性在阻抗平面上所占的面積越大，受振蕩的影響就越大。

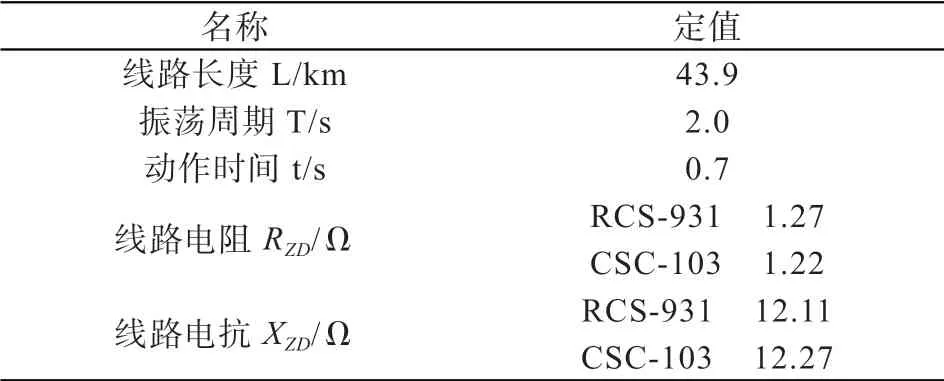
表1 系統仿真參數

圖6 中不同k 值情況下，測量阻抗經過圓特性曲線和四邊形特性曲線區域的時間如表2所示。根據圖6 可知，由于圓特性阻抗繼電器的動作范圍較大，所以在不同的k 值情況下測量阻抗通過該區域的時間均大于距離Ⅱ段保護動作整定時間0.7 s，將會造成阻抗繼電器本身動作；對于四邊形特性曲線，隨著k 值的增大，測量阻抗通過該區域的時間逐漸減少，其值小于保護動作整定時間0.7 s，繼電器本身將不會動作。因此，根據表2 同樣證明，由于兩種繼電器自身的特性差異，在系統振蕩期間，圓特性阻抗繼電器將更容易動作。

為保證電壓互感器在線路側時能可靠切除出口故障，在原有四邊形阻抗動作特性的基礎上，再疊加上一個包括座標原點的小矩形特性，稱為阻抗偏移特性動作區。小矩形動作區的X、R 取值見表3，其中XDZ 是相應元件的電抗定值，RDZ 是相應元件的電阻定值。結合表1 及表3 計算可得，距離Ⅱ段保護下阻抗偏移特性動作區為X 取2.5 Ω，R 取0.305 Ω，如圖6 中紅色矩形所示。由圖可知，即使四邊形阻抗動作特性中疊加阻抗偏移特性動作區，新疊加的動作區依舊無測量阻抗通過，即測量阻抗通過四邊形特性曲線區域的時間不變，與圓特性曲線相比后者更容易動作。

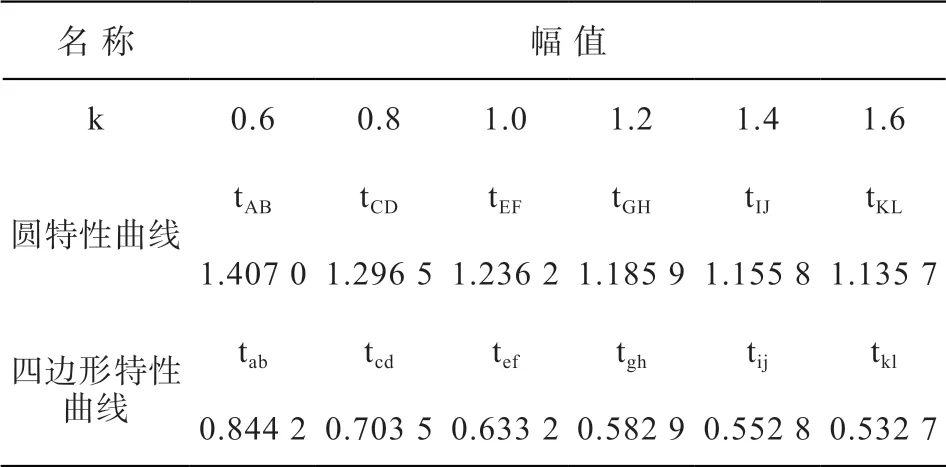
表2 測量阻抗進入保護動作區的時間

表3 四邊形阻抗偏移特性動作區定值

圖6 系統振蕩時M側測量阻抗的變化圖

4 結束語

分析了受系統振蕩影響，電網距離保護裝置安裝處測量阻抗的變化規律。并以此為基礎，利用圖形化方式直觀分析了不同動作特性阻抗繼電器造成繼電器本身動作的情況，比對了測量阻抗進入保護動作區的時間。計算結果表明，所得四邊形特性曲線能更好的防止系統振蕩期間距離繼電器動作。