基于改進在線序列極限學習機的AMI入侵檢測算法

劉菲菲,伍忠東,丁龍斌,張 凱

(蘭州交通大學 電子與信息工程學院,蘭州 730070)

0 概述

隨著電力工業和信息化技術的發展,智能電網成為未來電網的發展方向。智能電網是以電力和信息雙向流動為特征的網絡。高級量測體系(Advanced Metering Infrastructure,AMI)作為智能電網的核心組件通過與計算機網絡互連,實現電力數據的雙向通信。因為AMI系統存儲資源有限,而傳統入侵檢測方法部署成本高,所以網絡安全防護能力低,容易受到攻擊。一旦AMI被攻擊利用,用戶用電、控制數據、電價等信息就會被竊取,干擾電網正常運行,因此AMI網絡的安全研究具有重要的現實意義。

為保證AMI系統安全,NIST提出關于信息安全的研究報告[1]。目前,針對AMI的入侵檢測方法多數基于協議規范、安全需求和安全策略。文獻[2]針對AMI提出一種基于規則的入侵檢測系統,但此系統需要部署傳感器網絡,成本較高。文獻[3]提出基于數據挖掘的AMI入侵檢測系統,但需要在智能電表和收集器等系統中進行安裝。隨著機器學習技術的發展,基于機器學習的入侵檢測研究不斷被提出。文獻[4]利用支持向量機(Support Vector Machine,SVM)與人工免疫系統(Artificial Immune System,AIS)對惡意數據和可能的網絡攻擊進行檢測與分類,解決了分布式拒絕服務(Distributed Denial of Service,DDoS)攻擊AMI網絡的問題。文獻[5]在AMI網絡中引入蜜罐作為誘餌系統來檢測和收集攻擊信息。文獻[6]針對AMI提出一種基于數據流挖掘的入侵檢測系統,并對其性能進行分析。文獻[7]基于1/4超球體的單類支持向量機對AMI節點信任值的序列異常進行檢測。文獻[8]針對AMI異常用電檢測,提出K-means算法與PSO-SVM相結合的無監督分類算法。但SVM僅針對小樣本分類具有較好的分類效果,當面對AMI系統中存儲資源有限、采集數據量大和數據實時更新的情況時,SVM的分類效果并不理想。文獻[9]使用在線序列極限學習機(Online Sequential Extreme Learning Machine,OS-ELM)對AMI系統進行入侵檢測,通過數據樣本分批學習的方法,當新數據到達時刪除舊數據,從而降低訓練時間,減少AMI存儲資源占用。OS-ELM為AMI入侵檢測提供了一種新的解決方法。

可見,在OS-ELM算法中的學習參數需隨機設定,且OS-ELM算法容易出現過擬合問題,影響檢測準確率。另外,當OS-ELM算法面對海量數據時,由于數據特征過多,既無法保證重要特征的提取,又會增加訓練時間,因此本文提出一種基于改進在線序列簡化極核極限學習機(DBN-OS-RKELM)的AMI入侵檢測算法。

1 DBN-OS-RKELM算法

本文提出的基于DBN-OS-RKELM的入侵檢測算法整體框架如圖1所示,主要包括3個步驟:

1)數據預處理。將NSL-KDD數據集中的符號特征數據轉換為二進制數據,再歸一化至[0,1]。

2)深度信念網絡(Deep Belief Network,DBN)特征提取。無監督受限玻爾茲曼機(Restricted Boltzmann Machine,RBM)對標準化數據集進行預訓練,應用反向傳播(Back Propagation,BP)算法進行全局微調,得到降維后的特征向量。

3)OS-RKELM分類器。建立訓練網絡,在添加數據的過程中實時更新輸出權重并對攻擊進行分類。

圖1 DBN-OS-RKELM算法整體框架Fig.1 Overall framework of DBN-OS-RKELM algorithm

1.1 數據預處理

原始數據集NSL-KDD中存在多種類型的數據,因此在網絡訓練前需對數據進行預處理,將數據類型統一為網絡可識別類型,從而降低網絡訓練復雜度并提高訓練效果。

1.2 基于DBN的特征提取

DBN是由多層無監督RBM網絡和一層有監督BP網絡組成的深層神經網絡[10]。DBN相較于傳統神經網絡,既提高了提取重要特征的能力,又解決了訓練速度慢的問題,同時避免因隨機初始化權值參數而陷入局部最優的問題。因此,本文采用DBN進行數據特征提取。整個DBN訓練過程分為預訓練和權值微調。DBN結構如圖2所示,首先RBM逐層堆疊,將原始數據輸入最底層RBM進行訓練,將抽取的特征作為下一層RBM的輸入進行訓練,重復訓練直至迭代到最大迭代次數,將底層特征向高層特征轉化。在學習過程中,RBM降低至原始數據的維數,既保留了數據的主要特征,又降低了冗余特征。然后利用BP算法將錯誤信息自頂向下傳播至每一層RBM,并對RBM進行微調降低誤差。

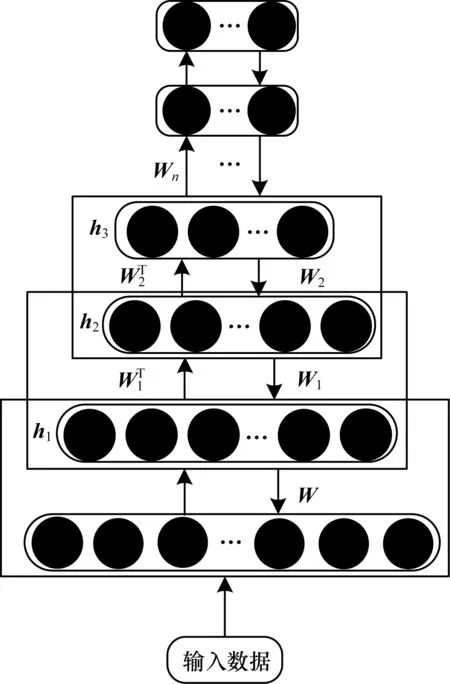
圖2 DBN結構Fig.2 DBN structure

1.2.1 RBM網絡預訓練

RBM是一個兩層神經網絡,分別包括可視單元(v)和隱藏單元(h),可視單元表示輸入數據特征。RBM每層之間為全連接,同層單元之間互不相連,RBM結構如圖3所示。其中,vi代表第i個可視單元的狀態,hj表示第j個隱藏層單元的狀態,wij是可視單元i和隱藏層單元j之間的權重,ai為可視層單元i的偏置,bj為隱藏層單元j的偏置。在預訓練過程中,使用貪婪無監督方法對RBM進行逐層訓練,使用激活函數sigmoid計算可視層與隱藏層間的概率取值。RBM預訓練過程的目標是求解出RBM模型中的參數θ,通常采用梯度下降法求解所有樣本的梯度和,但由于本文采用數據集的特征向量過多且計算量大,因此使用基于Gibbs采樣的對比散度方法求解更新后的參數θ。

圖3 RBM結構Fig.3 RBM structure

RBM采用對比散度方法進行網絡預訓練的過程[11]具體如下:

輸入可視層變量(v1,v2,…,vm)、學習率ε

輸出RBM參數θ={W,a,b}

步驟1將輸入的可視層變量(v1,v2,…,vm)賦值給v0。

1.2.2 BP權值微調過程

在RBM預訓練過程中,每一層RBM網絡只能保證權值對本層特征向量映射達到最優,并不能保證對整個DBN特征向量提取達到最優,因此本文基于BP算法利用少量帶標簽數據自頂向下有監督訓練DBN模型[12]。BP算法在權值微調過程中,將錯誤信息自頂向下傳遞至每一層RBM,計算樣本實際輸出值與期望標簽的誤差值,并將最大似然函數作為目標函數,調整各層權重,避免DBN陷入局部最優,改善神經網絡收斂時間長的問題,使DBN模型達到最優解,得到微調后的參數θ。BP權值微調過程具體如下:

輸入訓練樣本(v1,v2,…,vm),預訓練得到θ={W,a,b},學習率ε

輸出微調后參數θ={W,a,b}

步驟1對于vi的所有輸出單元οi,根據ξi=oi(1-oi)(ei-oi)求解其誤差梯度ξi(ei為期望輸出)。

1.2.3 網絡深度確定

(1)

根據文獻[13]可知,隨著網絡深度的增加,不相關部分被弱化,不同類樣本間的相關系數不斷減小,直至相關系數為-1.00時達到DBN最佳分類狀態,既保證了檢測效果,又減少了訓練時間,如圖4所示。本文從訓練集隨機抽取10 000條正常數據與攻擊數據確定DBN網絡深度,可以看出當隱含層層數為4時,互相關系數接近-1.00,之后一直趨于穩定,表明4層隱含層為最優深度,因此本文DBN的隱含層層數設置為4。

圖4 互相關系數與隱含層層數的關系Fig.4 The relationship between the correlation coefficientand the number of hidden layers

1.3 OS-RKELM分類器

1.3.1 基于OS-ELM的在線學習

神經網絡學習模型包括批量學習和在線學習兩種模式,極限學習機(Extreme Learning Machine,ELM)作為批量學習模型[14],將所有訓練數據一次性投入到模型中,這種模式需要的時間較多且效果不理想。因此,OS-ELM算法將訓練數據以數據塊的形式按時序分批次投入到網絡中進行學習。在新數據到達時,刪除已經學習過的數據,既減少了訓練時間,又避免了重復訓練。因此,OS-ELM算法符合AMI入侵檢測的需求[15]。

(2)

(3)

(4)

由文獻[14]可知:

(5)

按照這一規律不斷更新,加入新數據并刪除舊數據。當第K+1批數據到來時,得到此時的輸出權重為:

(6)

1.3.2 基于OS-RKELM的在線學習

在訓練過程中,OS-ELM算法只有當HHT為非奇異矩陣時,才可以求解隱含層權值矩陣,而在線學習過程中,添加的樣本總會出現新舊樣本過于相似的問題,導致HHT出現奇異現象,使訓練結果過擬合,影響最終檢測準確率。另外,OS-ELM算法的輸入權值和偏置都為隨機設定,泛化能力轉弱,對入侵檢測結果影響顯著。OS-RKELM是一種基于核函數的快速在線分類算法,其能夠以塊-塊的形式分批分類,通過正則化克服OS-ELM算法過擬合問題。與OS-ELM算法不同,OS-RKELM不限制初始訓練數據集大小[17],在任何初始訓練數據集下均可保持穩定的學習性能,同時加入核函數能夠減少隨機參數設定對檢測準確率的影響。可見,OS-RKELM算法具有更快的學習速率和更少的參數,不僅能夠解決OS-ELM算法存在的上述問題[18],而且滿足AMI入侵檢測的需求。

在OS-ELM算法的基礎上加入正則化,正則化是對最小經驗誤差函數加上約束條件,對誤差函數起到引導作用,減小解空間,使得參數達到最優解,具體計算公式如下:

其中,ε為實際輸出與理想輸出間的誤差,C為懲罰系數。根據KKT條件,將約束優化式(7)轉化為雙重優化問題,即:

(8)

由于網絡模型對學習參數進行隨機賦值,使得分類結果的泛化能力不理想,因此本文利用核函數將學習樣本映射到高維空間,提高分類準確性。定義核矩陣和輸出函數如式(9)和式(10)所示:

ΩELM=HHT=h(xi)h(xi)=κ(xi,xi)

(9)

(10)

根據KKT條件對上述約束條件進行求解,得到:

(12)

與OS-ELM相同,OS-RKELM包括初始化與在線學習兩個階段。

1)初始化階段

從原始輸入數據Ω=(xi,ti),i=1,2,…,n中選定新訓練數據Ω0=(xi,ti),i=1,2,…,M后進行訓練。計算初始階段的輸出層權值β0:

(13)

2)在線學習階段

在更新學習樣本后得到新的權值為:

(14)

其中:

(15)

K1=κ(X1,XM)

(16)

求得:

(17)

當第k+1批數據Ω=(xi,ti),i=k+1,k+2,…,n到達時,可以得到:

(18)

(19)

Kk+1=κ(xk+1,xn)

(20)

(21)

OS-RKELM分類器訓練流程如圖5所示。

圖5 OS-RKELM分類器訓練流程Fig.5 Training procedure of OS-RKELM classifier

2 實驗結果與分析

2.1 數據集預處理

本文針對AMI受到的攻擊類型,采用NSL-KDD數據集進行實驗。NSL-KDD數據集是目前得到廣泛應用的入侵檢測數據集。剔除KDD99數據集中的冗余部分得到新數據集,包含KDDtrain+訓練集(125 793條)和KDDtest+測試集(18 794條)兩部分[19]。數據集將攻擊類型分為Normal、DOS、U2R、R2L和Probe 5類,攻擊類型共有21種,各類攻擊樣本分布如表1所示。

表1 各類攻擊樣本分布Table 1 Distribution of various attack samples

數據集預處理過程具體如下:

1)數據集中包含41維特征,其中包括38個數字型特征與3個字符型特征。在數據訓練前,將字符數據轉換成二進制形式,例如將屬性特征protocol_type的3種類型分別用二進制表示為tcp[1,0,0]、udp[0,1,0]、icmp[0,0,1],將其余字符型特征都以二進制形式表示。

2)在數據分析前,利用歸一化方式將不同維度、性質的數據轉換為0～1,轉換公式如下:

(22)

其中,y為數據中某維度中的任意值,MAX為該維度中的最大值,MIN為該維度中的最小值。

3)將5種攻擊類型分別以對應的編碼映射表示為Normal[1,0,0,0,0]、DOS[0,1,0,0,0]、U2R[0,0,1,0,0]、R2L[0,0,0,1,0]和Probe[0,0,0,0,1]。

2.2 實驗評價指標

實驗采用準確率(AACC)、誤報率(FFPR)和訓練時間作為評價指標,具體計算公式如下:

(23)

其中,FFP為正常類預測樣本數量,TTP為攻擊類樣本數量,TTN為正確預測正常類樣本數量,FFN為攻擊類預測為正常類樣本數量。

2.3 實驗參數設置

DBN-OS-RKELM算法的參數設置如表2所示,本文采用RBF作為OS-RKELM的核函數。

表2 實驗參數設置Table 2 Setting of experimental parameters

本文實驗過程中正則化系數(γ)、懲罰因子(C)、隱含層個數(L)和新樣本數量(Batch)為隨機設定,對入侵檢測準確率結果有較大影響,如表3所示。通過多次實驗,將γ、C、L、Batch 4個參數分別進行循環測試,得到檢測準確率最高的參數作為本文最佳參數值。

表3 實驗參數隨機設置Table 3 Random setting of experimental parameters

2.4 結果分析

實驗從檢測準確率與訓練時間兩方面對DBN-OS-RKELM算法進行評價。為證明DBN-OS-RKELM算法的泛化能力和訓練速率,與ELM、OS-ELM和基于DBN的在線序列極限學習機(DBN-based Online Sequential Extreme Learning Machine,DBN-OS-ELM)算法進行比較。

實驗采用KDDtrain+訓練集和KDDtest+測試集對算法性能進行評估。首先在相同實驗平臺和特征數目的條件下,優化ELM、OS-ELM、DBN-OS-ELM和DBN-OS-RKELM算法參數,使其達到最佳值。為保證實驗準確性,每種算法運行20次,取平均值為最終結果。

實驗1分別比較OS-ELM、DBN-OS-ELM和DBN-OS-RKELM這3種算法的隱含層對檢測準確率的影響,如圖6所示。DBN-OS-RKELM算法在隱含層節點為100時準確率最高。隱含層節點個數對OS-ELM算法準確率影響較明顯,這是因為作為單隱層網絡結構,隱含層個數對分類結果的影響很大。若隱含層節點個數過少,則網絡達不到預期的學習能力與檢測效果;若隱含層節點個數與特征維度過多,增加了訓練時間和網絡復雜度,導致泛化能力降低,則會造成過擬合現象。DBN-OS-ELM算法在隱含層節點個數達到70之后,準確率下降,并保持趨于穩定的狀態,因此實驗中選取的DBN-OS-RKELM和OS-ELM算法的隱含層個數為100,DBN-OS-ELM算法的隱含層個數為70。

圖6 網絡隱含層節點個數與檢測準確率的關系Fig.6 Relationship between the number of hidden layernodes in the network and detection accuracy

實驗2分別將ELM、OS-ELM、DBN-OS-ELM和DBN-OS-RKELM這4種算法在相同測試集與訓練集上進行實驗。如表4所示,OS-ELM算法與ELM算法相比,在減少訓練時間的同時檢測準確率有所降低;DBN-OS-RKELM與ELM算法相比,在檢測準確率上提高了3.36%,而且其訓練時間與OS-ELM算法相比變化不大,這是因為DBN特征提取降低了數據維度,并且在OS-RKELM中進行了數據分塊和實時學習,進一步減少了訓練時間。與OS-ELM、DBN-OS-ELM兩種算法相比,DBN-OS-RKELM算法增加了數據特征提取和最優參數搜索過程,其檢測準確率的提升表明算法整體性能優于傳統極限學習機方法。

表4 4種算法的入侵檢測性能對比Table 4 Comparison of intrusion detection performanceof four algorithms

實驗3將攻擊類型分為Normal、DOS、U2R、R2L和Probe 5類,對ELM、DBN-OS-RKELM、EDF和CNN算法在KDDtest+測試集下的性能進行對比,其中EDF和CNN實驗數據來自文獻[20]。由表5可以看出,DBN-OS-RKELM算法的檢測準確率得到提升,同時大幅降低了訓練時間。這是因為在通過特征提取和隨機參數尋優后,數據維度降低,計算復雜度也隨之降低。DBN-OS-RKELM算法與EDF和CNN算法對于Normal、DOS和Probe攻擊類型的檢測準確率十分接近,而對U2R和R2L攻擊類型的檢測效果更好,且訓練時間也不會因為識別種類的增加而增加,依舊保持在線學習訓練耗時短的優勢。對于U2R和R2L攻擊類型的檢測準確率相對較低的原因為:U2R和R2L攻擊類型訓練集中的數據量過少,以及分類器在學習過程中得到特征向量的信息過少,因此在識別過程中容易被識別為其他攻擊類型。

表5 5種攻擊類型的入侵檢測性能對比Table 5 Comparison of intrusion detection performance offive types of attacks

3 結束語

本文提出DBN-OS-RKELM算法，將AMI中采集到的日志信息利用DBN提取重要數據特征,應用OS-ELM對實時入侵數據以塊的方式進行在線更新分類以縮短檢測時間,并通過加入核函數與正則化提高極限學習機的泛化能力。實驗結果表明,DBN-OS-RKELM算法解決了OS-ELM算法在檢測過程中通過犧牲檢測準確率降低訓練時間的問題,相比ELM算法在保持準確率的同時大幅降低了訓練時間,相比EDF和CNN算法入侵檢測準確率更高,體現出其在海量樣本情況下實時學習的性能優勢,且更適用于智能電網AMI的實際應用。后續可將DBN-OS-RKELM算法應用于智能電網AMI入侵檢測實驗平臺,以驗證其正確性與高效性。