基于CNN 和粒子群優化SVM 的手寫數字識別研究

楊 剛，賀冬葛，戴麗珍

（華東交通大學電氣與自動化工程學院，江西 南昌330013）

手寫體數字識別在銀行、稅務和郵政系統等領域有著重要的應用和廣闊的發展前景，尤其在脫機工作環境下有很大的提升空間[1]。 傳統的手寫體數字識別方法主要有支持向量機[2-4]，神經網絡算法[5-6]等。 但由于手寫數字本身所包含的特征較少，加上不同人書寫數字字符差異較大，在識別率方面具有較大的提升空間。以深度學習為代表的機器學習方法的出現[7]，大大降低了圖片識別的難度，為手寫體數字識別提供了有效工具。卷積神經網絡由于其“深層結構”的優勢，常被用于圖片特征提取，并通過Softmax 對相關特征進行分類。盡管該方法具有較理想的處理效果，但對電腦要求過高，且計算復雜、耗時較長。 為了提高手寫體數字的識別率，本文擬結合卷積神經網絡的特征提取能力、支持向量機的分類能力、粒子群優化的尋優能力，通過CNN 對手寫體數字圖片進行特征提起，采用粒子群優化SVM 關鍵參數對數字特征進行識別，從而實現手寫體數字的識別。

1 卷積神經網絡

卷積神經網絡（convolution neural network，CNN）[8]是一種前饋神經網絡，它的人工神經元可以響應一部分覆蓋范圍內的周圍單元，對于大型圖像處理有出色表現。

CNN 是一個受生物視覺啟發、以最簡化預處理操作為目的的多層感知器的變形，它結構的可拓展性很強，可以采用較深的層數，構成的深度模型具有更強的表達能力[9]。 卷積神經網絡由一個或多個卷積層（convolution layer）和末端的全連接層組成，同時也包括關聯權重和池化層（pooling layer）。 這一結構使得卷積神經網絡能夠利用輸入數據的二維結構，并且也可以使用反向傳播算法進行訓練。 相比較其他深度、前饋神經網絡，卷積神經網絡需要考量的參數更少，使之成為一種頗具吸引力的深度學習結構[10]。

1.1 卷積層

卷積層的主要作用是通過對卷積核大小的設置，由淺入深不斷對前一層傳輸的數據進行特征提取。 由于設置了共享權值，在同一特征圖中神經元使用同一組卷積核，可以減少訓練參數。 其中，卷積核數值在初始化后由后續的網絡訓練確定[11]。

圖片各像素點的值與卷積核的乘積加入偏置后經過激活函數的運算即可得到圖片的一個特征映射：

其中：ajL表示L 層卷積后第j 個神經元的輸出；wijL表示卷積核；bjL表示偏置。 f（·）為神經元激活函數，這里我們采用Sigmoid 函數，即

1.2 池化層

池化是卷積神經網絡中的一個重要操作，能夠減少圖片中冗余特征，同時保持特征的局部不變性[12]。

圖片經過卷積處理后，每個n×n 鄰域內的像素點采用最大池化（MaxPooling）的方法變為一個像素

其中：down（·）表示下采樣函數，該層運算不包含可學習的權值和閾值。

1.3 全連接層

全連接層可以整合前向傳來的具有類別區分性的局部信息；同時，可以增強網絡的非線性映射能力；限制網絡規模的大小。

2 支持向量機

支持向量機是建立在統計學理論基礎上的一種數據挖掘算法， 其工作機理是尋找一個滿足分類要求的最優分類超平面， 使得該超平面在保證分類精度的同時， 能夠使超平面兩側的空白區域最大化。 理論上，支持向量機能夠實現對線性可分數據的最優分類[13]。其原理示意圖如圖1 所示。

本文使用LIBSVM 工具箱通過一對一的方法來實現分類器的設計構造。 當要對一個未知類別樣本分類時，輸出結果值最大的即為該樣本類別[14]。

經過多年來國內外的研究表明，SVM 以RBF核(徑向基函數)為核函數具有很強的學習能力和分類效果。 文中選用RBF 作為SVM 的核函數

圖1 支持向量機示例Fig.1 Example of support vector machines

2.1 基于的SVM 的參數優化

在用SVM 做分類預測時若想要提高結果的準確率往往需要對SVM 參數進行優化以選取最優的參數[15]（主要是懲罰參數c 和核函數參數g）。

SVM 中懲罰系數c（c 為正數) 用來表征對誤差的寬容度；c 值過高或過低均會影響SVM 的泛化能力。參數g 是選擇RBF 函數作為Kernel 后該函數自帶的一個參數，隱含地決定了數據映射到新的特征空間后的分布。

PSO 首先是在可行解中初始化一群粒子，每個粒子都有自身的速度、位置跟適應值，通過不斷的迭代搜索最優解。 在每一次迭代中粒子通過個體最優值跟全局最優值來更新自己。

對于隨機初始化產生的粒子，將其視為第一代初始種群，通過目標函數Q（Xi）計算得出的適應度值來衡量種群Xi的優劣。 種群中粒子i 當前最優位置為

其中：Xbesti為粒子i 所經歷的最優位置標記；Qbesti為粒子i 位置最優時所對應的適應值。 尋優過程中，粒子不斷更新自己的位置跟速度，速度更新公式為

其中：Xbestg為粒子g 所經歷的最優位置標記（對應的適應度值應為Qbestg此處沒有體現），Vmax為粒子單步更新的速度最大值；c1、c2為加速度常數， 表示PSO 參數局部搜索能力；r1、r2是兩個相互獨立的隨機參數；w為慣性權重，在優化過程中能夠起到提高全局搜索跟局部搜索的作用。

位置更新公式為

其中xi=（xi1，xi2，...，xin）表示粒子i 位置向量中的值。

適應度函數的確定是實現PSO 算法的先決條件，更是尋優的依據。 傳統方法是尋找或者設計一個函數用以計算適應度值，以顯示尋優效果的優劣[16]，但計算復雜，使用困難。本文使用CV 算法，將對訓練集在CV意義下的準確率作為粒子群中的適應度函數值。

2.2 交叉驗證

交叉驗證（CV）是一種常用的驗證分類器性能的統計分析方法[17]。 關于對SVM 參數的優化選取是將c和g 在一定的取值范圍內取值，然后將訓練集作為原始數據采用K-CV 的方法對SVM 進行訓練，訓練后得到的模型再通過驗證集驗證后得出分類準確率，準確率最高的模型即為最佳參數。 對于可能出現的過學習狀態的發生我們選擇最佳參數中懲罰參數c 最小的一組（c，g）參數為最優參數。

這里將對訓練集進行CV 意義下結果中最好的模型識別準確率作為PSO 的適應度值。 基于PSO 的SVM 全局參數尋優的整體算法過程如圖2 所示。

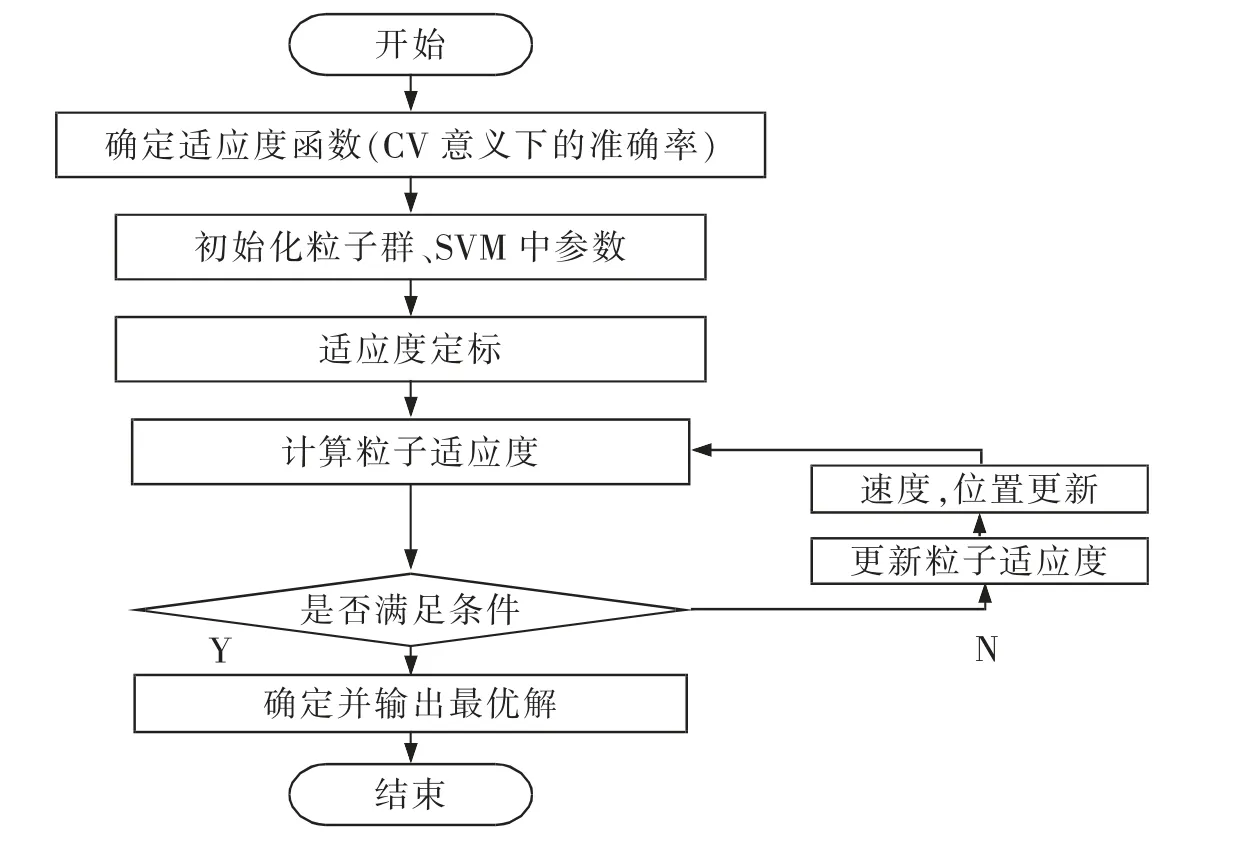
圖2 PSO 優化SVM 參數流程圖Fig.2 Flow chart of PSO optimized SVM parameters

3 基于CNN 和PSO-SVM 的手寫數字識別

為提高網絡對手寫數字圖像的識別精度，本文將卷積神經網絡和支持向量機結合，并通過PSO 優化算法優化SVM；PSO 是基于個體間的協作實現搜索空間中的尋優，能很好的提高SVM 的識別性能。

在使用粒子群優化SVM 參數的實驗中，相比于隨機初始化粒子確定適應度值，本文使用CV 意義下的準確率將其代替，以達到快速收斂的效果。 整體結構如圖3 所示。

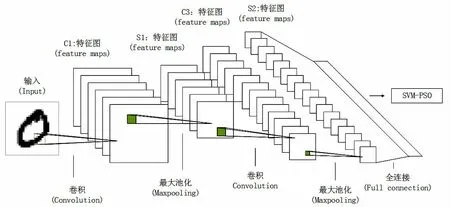
圖3 CNN-SVM 整體結構圖Fig.3 CNN-SVM overall structure diagram

基于CNN 和PSO-SVM 的手寫數字識別流程主要步驟如下:

Step1：將手寫數據集分為訓練集和測試集;

Step2：通過Python 程序將二維圖片數據傳入卷積網絡輸入層；

Step3：圖片經過卷積層、池化層得以特征提取跟降維，得到含有特征信息較高的數據集，經全連接層后，數據由二維轉換為一維；

Step4：將全連接后的一維數據通過Matlab 傳入SVM;

Step5：使用K-CV 的方法將一維的訓練數據作為訓練數據得到當前組（c，g）的分類準確率，并將其作為PSO 中粒子的適應度函數；

Step6：根據粒子群對SVM 參數的不斷尋優，最終確定出最佳的c，g 參數（尋優過程如圖4 所示）；

Step7：訓練完成后將一維的訓練集送入最終的模型中進行分類驗證，以最終對手寫數字圖片的分類準確率作為最后的結果。

4 實驗與分析

本文設計構建的卷積神經網絡包含兩個卷積層、 兩個池化層和一個全連接層， 分類層采用優化后的SVM 分類器。

通過使用UCI 提供的Semeion 手寫數字集及經典MNIST 手寫數字集分別對網絡進行訓練。兩數據集均將圖片分為0～9 十類，圖片顯示的手寫阿拉伯數字即為該圖片的屬性類別。 實驗中卷積核大小設置為5×5，池化層中采樣大小為2×2。

4.1 Semeion 手寫數字數據集

UCI 提供的Semeion 手寫數字數據集共有80 人參與，每人在非刻意的情況下在紙上快速將數字0～9 手寫2 次。 數據集共有1 593 張圖片，從中隨機抽取1 500 張圖片進行實驗并將其分為訓練集跟測試集， 訓練集共有700 張圖片，測試集有800 張圖片；圖片為16×16 像素的一維灰度圖片。 每張圖片均采用固定閾值將像素點縮放為二進制(1/0)值。 圖4 為該數據集石示例圖片。

圖4 部分手寫數字圖像Fig.4 Partial handwritten digital images

實驗主要是通過使用粒子群對SVM 中的參數不斷尋優，以提高分類識別層的識別準確率。 參數c、g 均在一定范圍內取值，于是我們根據實驗經驗設定c∈[0，100]，g∈[-100，100]，通過初始化選取20 個種群，經過200 次迭代尋優。

實驗中我們隨機將測試數據集均分為8 組，每組100 個樣本進行實驗仿真，實驗結果如圖5～圖6 所示。

可以看到100 組圖片中只有一張未能識別正確；通過測試驗證可知該模型對數字的識別率達99.11%，PSO 尋優最佳參數為c=2.297，g=0.01。

在手寫數字識別的實驗中，對于每組能夠正確識別的圖片個數n 將其除以每組圖片總數m，得出該組下的識別正確率p，即p= n/m×100%。 至此，將相同的訓練測試數據試驗在不同的模型中進行對比，結果如表1～表2，圖7 所示。

圖7 UCI-Semeion 數據集實驗結果Fig.7 Experimental results of UCI-Semeiondataset

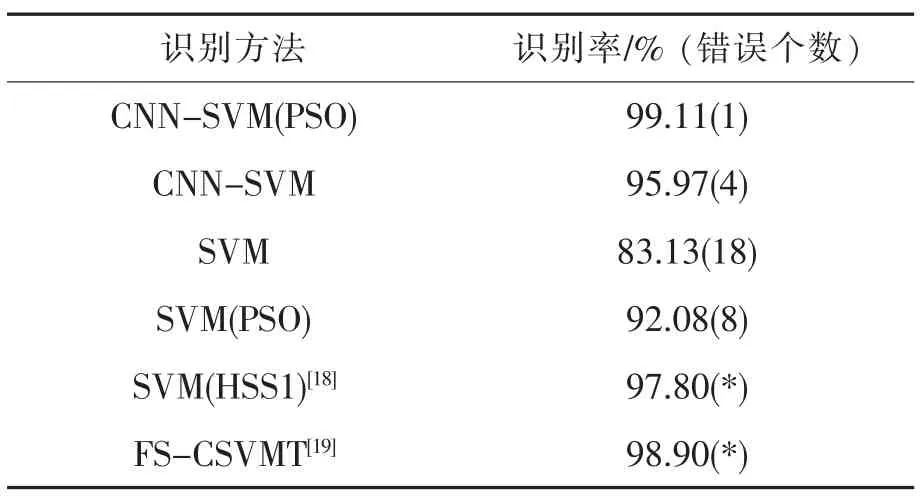
表2 UCI 數據集識別率Tab.2 UCI data set recognition rate

可以看出經過PSO 參數優化后的卷積神經網絡結合支持向量機算法精度最高，均保持在95%以上，對處理圖片分析上具有一定的優勢。

文獻[18]顯示為SVM 在不同特征情況下在該數據集中的識別精度(文獻中實驗未顯示識別錯誤個數)，可以看到在對SVM 加入不同特征后，本文算法識別正確率仍然高于文獻[18]中對應的識別算法。文獻[19]中提出了一種基于邊界對特征的敏感度值進行特征選擇的支持向量機樹混合學習模型，其識別率為98.9%。

4.2 MNIST 數據集

MNIST 手寫數據集包含70 000 個樣本，每個樣本為28×28 像素的灰度圖片，其中訓練集有60 000 張圖片，測試集有10 000 張。 圖8 為該數據集的部分樣例。

由于數據集數據樣本較多，此次實驗隨機從數據庫中選取600 張訓練圖片，1 000 張測試圖片，并將測試集隨機分為十等份(每份100 張圖片)進行測試驗證。 表3 顯示十份驗證集中最優識別情況。

由實驗結果可知，本文中采用的方法識別率最高為96%，即100 個隨機選取的數據樣本中只有4 個未能識別正確。文獻[20]使用SOM 簡化算法及并行電路架構，采用1 000 組數據進行測試，得到84.13%的準確率。文獻[21]中設計了分數階梯度下降學習機制，在分數階BP 神經網絡中自適應更新連接權值，最終提出的PEO-FOBP 在MNIST 數據集中識別精度有96.54%其對應的未加入極值優化的自適應的PEOBP 算法識別度為95.67%。

對以上實驗進行分析可看到，CNN 結合PSOSVM 的算法對分類識別手寫數字圖片有良好的效果，在一定程度上提高了對圖片的的識別率。

圖8 MNIST 數據集部分樣例Fig.8 Partial sample of MNIST dataset

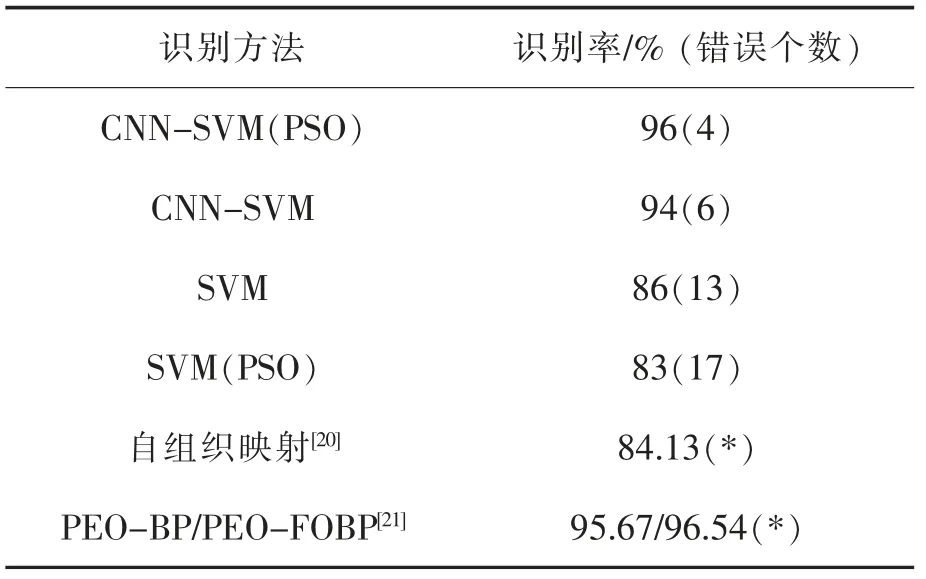
表3 MNIST 數據集識別率Tab.3 MNIST dataset recognition rate

5 結束語

本文提出使用卷積結合支持向量機的方法對圖片進行識別，并采用基于K-CV 作為適應度函數的PSO對SVM 參數進行優化，以此提高支持向量機的識別性能。

在圖像識別的問題中，卷積神經網絡通過自身深度學習的能力獲取圖像特征，對圖像有較高的識別率；傳統卷積神經網絡使用Softmax 進行分類識別，Softmax 屬于線性模型，本身具有分類速度快、模型占用空間小等優勢，但使用較強的線性假設，在分類問題上仍有一定的提升空間；進行計算時涉及指數函數的運算，當函數增長時過高的函數值將影響計算機的輸出結果，因此對計算機硬件設備有一定的要求。

實驗采用Python3.5 與Matlab2015b 作為實驗平臺， 對UCI 提供的手寫圖片和MNIST 手寫數據集進行分類識別。在確定最佳參數c、g 的值后，最終對兩款測試集的識別率分別達到99.11%和96%。然而，在實驗過程中也遇到一些問題，比如實驗設備比較老舊，對于更復雜的程序難以順利運行(更深層次的卷積神經網絡對硬件設備要求較高)，像MNIST 這樣文件較大的數據集也很難實現。但對于該次實驗設計的網絡結構較為簡單且實驗結果表明該算法識別性能較好，對手寫數字正確識別率有一定的提高，因此該算法在研究領域有深入研究的潛在價值。