基于聯合抗噪算法的滾動軸承故障診斷研究

劉 沖

（華東交通大學電氣與自動化工程學院，江西 南昌330013）

滾動軸承廣泛存在于機械設備，由于滾動軸承的工作環境惡劣且噪聲情況復雜，故障尺寸微小又難以直接觀察，業界普遍采用數據驅動的方式實現故障診斷，但是振動信號易受噪聲污染，使得有效特征難以被提取，因此如何提高滾動軸承在復雜噪聲環境下故障診斷的準確性，成為了當前研究熱點。

隨著計算機、傳感器的迅猛發展，機械設備的狀態檢測進入了“大數據”時代[1]。 使得故障診斷技術向深度學習方向發展。 深度學習模型依靠其多個隱含層，在特征提取和分類方面的卓越表現，在故障診斷領域取得了較多研究成果。 Long 等[2]將原始振動信號轉換為二維圖像，使用LeNet-5 模型對二維圖像進行故障診斷。 2016 年Turker 等[3]提出了一種含有3 個改進的卷積層和2 個全連接層的一維卷積神經網絡，直接以原始電流信號為輸入，準確率達到了97.2%。 Chen[4]提出了一種單卷積層和2 個全連接層的二維卷積神經網絡模型，并將算法應用于齒輪箱故障診斷。 張西寧，向宙等[5]用堆疊卷積自編碼進行軸承故障診斷，使得診斷精度從79.9%提高到92.1%。 向宙等[6]用改進的區分自編碼網絡對不同工況下的軸承數據進行診斷，使得所提出的區分型網絡的特征提取能力不受工況影響。 雖然很多基于卷積神經網絡的研究已經取得較好診斷效果，但僅證明了模型在使用無噪聲實驗數據的有效性。然而，振動信號易受噪聲污染。近年來，為了提高模型的抗噪能力，一些訓練技巧(如使用dropout 操作[7]）和結構改進(如添加AdaBn 層[8]）的方法被提出來，在圖像降噪領域，Zhang 等[9]提出一種基于深度卷積神經網絡的非固定噪聲模板圖像訓練方法。 Mao[10]等提出了一種基于深度卷積去噪自編碼的圖像降噪方法。 然而這些方法僅適用于二維或者三維圖像的降噪。 目前針對一維振動信號降噪的方法大多基于信號處理技術，如黃正平等[11]提出一種基于MED 和Teager 能量算子的故障診斷模型，能有效消除信號的帶內噪聲，但是信號處理技術過于依靠人工特征提取，費時費力。 因此，本文提出一種基于全卷積網絡（fully convolutional networks，FCN）[12]的一維卷積降噪自編碼器（1D-convolutional denoising auto-encoder ，1D-DCAE）與一維卷積神經網絡（1-D convolutional naural network，1D-CNN）聯合的診斷方法來解決上述問題。 前者對原始信號降噪，后者對1D-DCAE 輸出的降噪信號進行故障診斷。此外，1D-DCAE 模型了舍棄池化層以減少1D-DCAE 在數據重構過程中造成的信息丟失，從而提升降噪能力。

1 卷積降噪自編碼和卷積神經網絡結構

1.1 一維卷積神經網絡

卷積神經網絡（convolitional neural network，CNN）是一種多模塊的前饋神經網絡，傳統CNN 的結構主要由特征提取模塊和分類模塊2 個部分組成，特征提取模塊由輸入層、卷積層、激活函數、池化層組成，分類模塊包含全連接層和分類層。 特征提取模塊的作用是從數據中提取特征，分類模塊實現對隱層特征的回歸和分類。 卷積層是CNN 提取特征的關鍵，卷積層由一組濾波器組成，濾波器由多個神經元組成，神經元都只與輸入層中的神經元局部連接， 且每個濾波器中的神經元共享權值， 這也是CNN 能減少網絡參數的根本原因。 第k 個濾波器的濾波操作的公式為

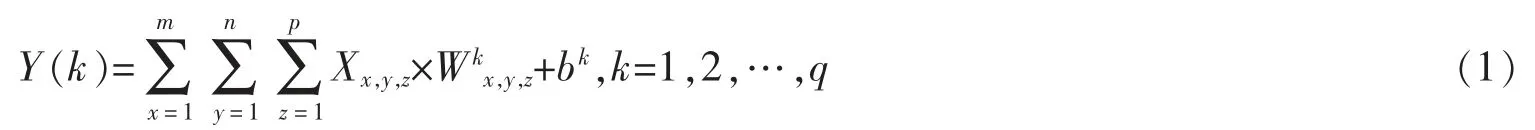
式中：Y（k）為第k 個濾波器學到的特征圖；X 為輸入；x，y，z 為輸入數據的維度；Wkx，y，z，bk為第k 層的權重和偏置。

卷積層的輸出經ReLu 函數激活后輸入池化層，池化層是下采樣的過程，其作用是對卷積層學習到的特征降維，提取重要紋理特征。全連接作用是將特征提取模塊學習到的分布式特征表示映射到樣本標記，起到分類器的作用，但由于其龐大的參數量可能會導致網絡陷入擬合，大量的參數也會大量增加訓練時間，影響算法的時效性。 針對以上的問題，1D-CNN 采用全局平均池化(global average pooling)作為分類器，全局平均池化能對特征提取模塊學習到的高維特征直接降維，因其本身沒有可供學習的特征，于傳統的全連接層相比，全局平均池化極大地減少了網絡的參數。

聯合診斷模型基于1D-CNN 來診斷滾動軸承故障，1D-CNN 的模型和參數如圖1 所示，模型由3 個卷積層、2 個最大池化層、1 個全局平均池化層組成，在特征學習方面采用卷積層和池化層交替來實現，分類器選用的是全局平均池化層而不是傳統的全連接層。 其中，20@32 表示該層使用32 個長度為20 的卷積核進行卷積運算，模型的卷積核和池化核均為一維結構，以適應一維振動信號。

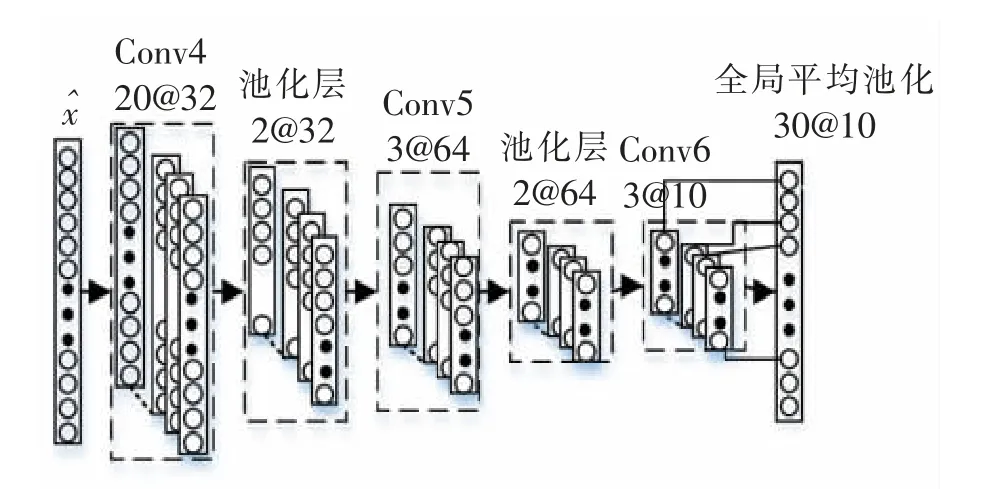
圖1 1D-CNN 結構Fig.1 Structure of 1D-DCAE

1.2 一維卷積降噪自編碼

傳統的自編碼器（auto encoder，AE）由編碼器和解碼器兩部分組成，編碼器經非線性映射對輸入X 降維，得到隱藏層表示Z，解碼器由另一個非線性變換將隱藏表示Z 映射回重構數據

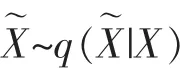
傳統的DAE 是基于全連接網絡的，但是全連網絡參數過多，網絡容易陷入過擬合。 針對該問題，本文提出一種基于FCN 的1D-DCAE 模型。FCN 是一種特殊類型的卷積神經網絡，FCN 和CNN 兩者之間的區別是FCN 移除了全連接層，與基于全連接層的DAE 相比，FCN 主要優勢有兩點：①移除全連接層能減少參數數量和網絡過擬合風險；②FCN 使得每個輸出特征圖相互關聯，能保留原始輸入的局部空間信息。 此外，為了讓輸入和輸出信號精準匹配，基于FCN 的1D-DCAE 模型沒有使用池化層，因為池化層可能會造成信息的少量細節丟失[14]。

本文使用1D-DCAE 對含噪信號做降噪處理，以聯合診斷模型的抗噪能力，與CNN 類似，1D-DCAE 也能通過增加深度來提升重構能力。

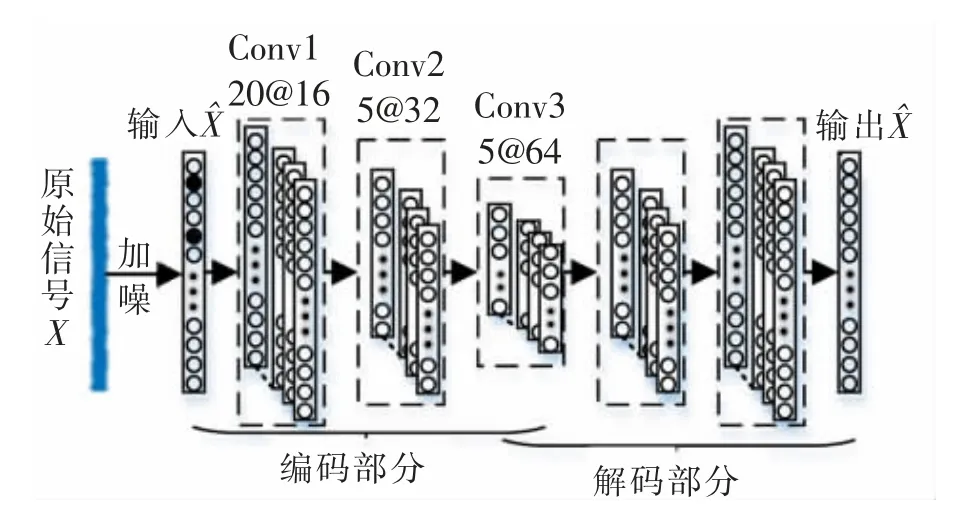
圖2 1D-DCAE 結構Fig.2 Structure of 1D-DCAE

式中：Pz為原信號功率；Pn為噪聲信號功率。

1.3 1D-DCAE 和1D-CNN 的聯合診斷流程

基于聯合算法的診斷流程主要分為5 個階段：①以1 dB 為間隔，在原始數據集中分別加入SNR=-2～9 dB 范圍的高斯白噪聲，共得到11 種不同的噪聲信號；②將得到的每種噪聲分別按4∶1 分為訓練集和測試集，將SNR= -2，0，2，4，6，8 dB 環境下的6 種噪聲訓練集混合并洗牌，用于訓練1D-DCAE，所有的測試集用于測試模型性能；③用混合高斯噪聲的訓練樣本x?對1D-DCAE 訓練，完成1D-DCAE 的訓練后，得到降噪的訓練樣本x?；④將降噪后的訓練樣本x?作為1D-CNN 的輸入，利用訓練樣本標簽完成模型訓練；⑤將測試樣本輸入聯合診斷模型，完成軸承故障的診斷。

2 實驗驗證

2.1 數據描述

實驗所用滾動軸承時域振動信號來自美國西儲大學軸承中心，信號采樣頻率為12 kHz。 故障類型為內圈故障、外圈故障、滾球體故障，故障的損傷直徑分別為0.18，0.36，0.54 mm 三種程度故障，有9 類故障加正常狀態共計10 類數據樣本。 本次所有實驗數據均在0 負載情況下采集，每0.1 s 采集一次數據，每個樣本長度為1 200 個數據點，每類樣本采集1 000 個，共計10 000 個樣本，其中4/5 的樣本用于訓練，其余的樣本用于測試。 實驗使用深度學習框架Tensorflow，處理器為i7-4790@3.60 GHz，內存為8 GB 硬件平臺進行實驗。

2.2 基于1D-DCAE 的降噪實驗

本文實驗結果由兩部分組成：一部分為1D-DCAE 的重構誤差，另一部分為1D-CNN 的診斷精度，以此來驗證聯合抗噪算法的有效性。 前者重構誤差所反映的是1D-DCAE 降噪效果，后者診斷精度驗證了本文算法在噪聲環境下的診斷效果。

1D-DCAE 訓練參數和超參數設置如下：學習率設為0.01，epochs 設為50，batchsize 設為100，DAE 的輸入、隱藏層、輸出維度分別設為1 200，600，1 200，激活函數為ELU。 為了驗證池化層對1D-DCAE 算法去噪效果的影響，將本文提出改進的1D-DCAE 與經典1D-DCAE 的進行比對，除了含有池化層之外，其余參數與改進的1D-DCAE 算法一致，每組實驗重復10 次，實驗結果如表2 所示。

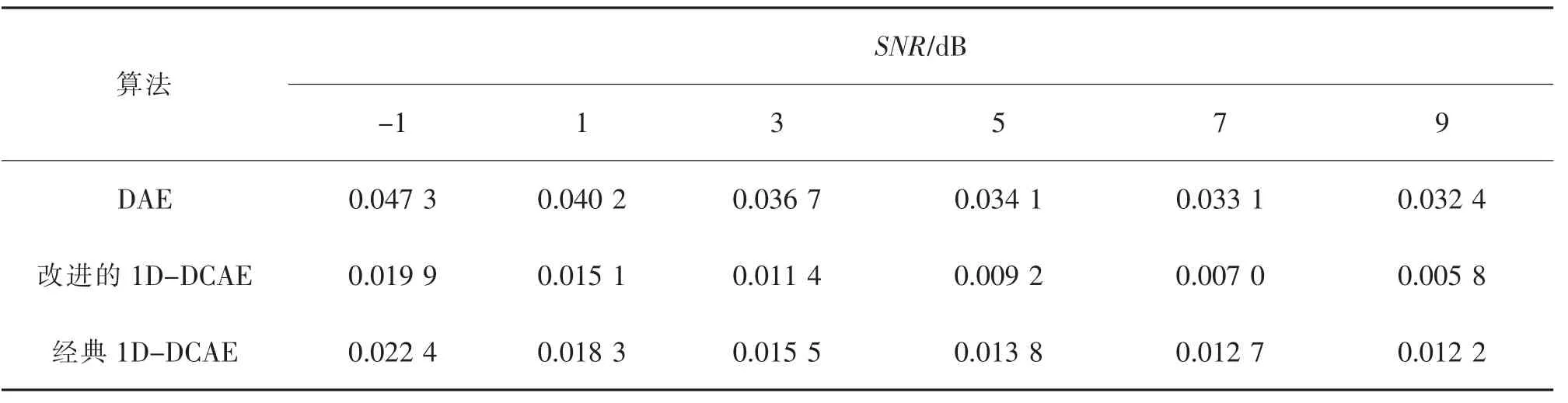
表1 在不同信噪比下DAE 和1D-DCAE 的重構誤差Tab.1 Reconstruction errors of DAE and 1D-DCAE under different SNR

由以上實驗結果可知， 在所有信噪比環境下， 改進的1D-DCAE 的重構誤差均小于DAE 和標準的1D-DCAE 算法。 實驗結果表明， 改進的1D-DCAE 算法降噪效果最好， 卷積自編碼模型去噪能力強于DAE，原因如下：①由于1D-DCAE 的結構較深，其特征重構能力優于DAE；②1D-DCAE 的參數遠少于DAE。 其中，1D-DCAE 的參數數量為2×（20×16+5×32×16+5×64×32）=26 240，DAE 的參數數量為1 200×600×2=1 440 000，所以1D-DCAE 算法在噪聲環境下不易過擬合。 當SNR>5 dB 時，改進的1D-DCAE 算法的重構誤差隨著信噪比的增加不斷減小，而標準1D-DCAE 的重構誤差幾乎沒有變化，其原因是在高信噪比環境下，標準1D-DCAE 造成信息丟失大于降噪得到的收益。 因此，舍棄池化層能提升對振動信號的降噪效果，并且減少模型對輸入數據的信息丟失。

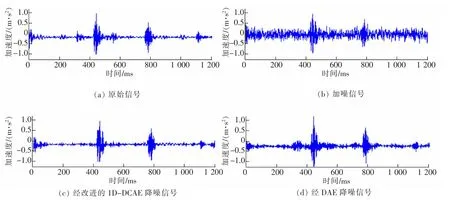
圖3 信號圖Fig.3 Figures of signals

2.3 聯合算法的故障診斷

本文使用1D-CNN 對降噪信號進行故障診斷，1D-CNN 的訓練參數和超參數設置如下：epochs 為120，學習率為0.001，batchsize 為100， 重復10 次實驗，1D-CNN 在不同信噪比條件下的診斷結果如圖4 和表2所示，在SNR=-1 dB 時的診斷高達96.2%，SNR>1 dB 時，診斷精度能達到98.5%以上。 因此，聯合診斷方法能自適應的處理任何噪聲環境，即使是較低信噪比的噪聲環境下。

為了驗證本文聯合診斷方法的有效性，本文算法與DCE+1D-CNN，未降噪處理+1D-CNN 進行實驗結果的比對，在SNR= -1 dB 噪聲環境下，DCE+1D-CNN 聯合診斷的方法和1D-CNN 的診斷正確率分別下降至93.86%和84.55%。 實驗結果表明， 在低信噪比環境下， 本文所用的1DDCAE 對數據進行降噪處理，能有效的提升診斷精度。

圖4 1D-CNN 在不同降噪方法下的診斷精度Fig.4 Diagnosis accuracy of 1D-CNN with different denoising processes

表2 1D-CNN 在不同降噪方法下的診斷精度Tab.2 Diagnosis accuracy of 1D-CNN with different denoising processes %

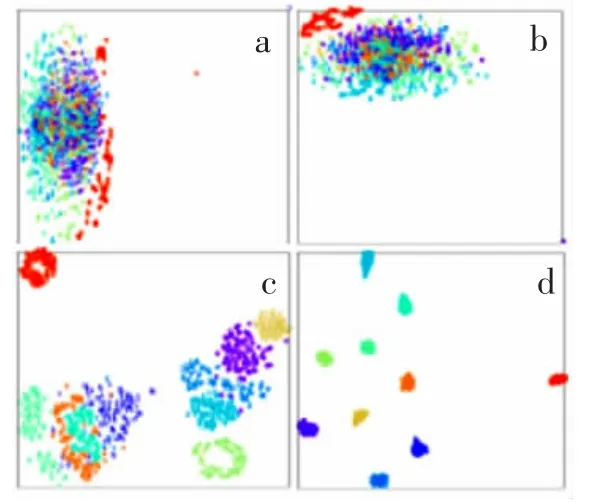
圖5 t-SNE 特征學習可視化Fig.5 Feature learning visualization with t-SNE

2.4 特征可視化

本文為了證明1D-CNN 在噪聲環境下的特征提取能力，在SNR=1 dB 的噪聲環境下，采用了t 分布隨機近鄰嵌入流形學習算法（T-SNE）將特征降維至2 維，對輸入層和三個卷積層進行特征可視化， 其中每一種顏色表示一種故障類別，每一個點表示一個樣本， 可視化結果如圖5 所示，a，b，c，d 從左至右分別為輸入，Conv4，Conv5，Conv6 的特征可視化結果。

3 結論

提出一種基于1D-DCAE 和1D-CNN 聯合抗噪診斷算法。 該方法能有效解決復雜噪聲環境下的故障診斷問題，提高了系統的抗噪能力。 對實驗結果進行分析得出以下結論：

1） 基于FCN 的1D-DCAE 對于軸承信號的降噪效果均優于傳統DAE 和經典DCAE 算法， 即使在SNR= -1 dB 低信噪比環境下，1D-DCAE 算法的重構誤差僅為0.019， 在SNR>5 dB 的高信噪比環境下，重構誤差小于0.01，表明本文提出算法在舍棄池化層后，在數據重構過程幾乎沒有造成信息丟失。

2） 經1D-DACE 降噪后，1D-CNN 即使在SNR= -1 dB 低信噪比噪聲環境下， 其診斷精度達到了96.2%，SNR>1 dB 時，診斷精度能達到98.5%以上，若未作降噪處理，其診斷精度僅為84.6%。 結果表明聯合診斷算法能實現對各種噪聲環境下的故障精準診斷。