Maxwell 方程特征值問題的譜方法
陳亞飛,茆晉晉
(1. 淮北師范大學數學科學學院,安徽 淮北235000 ;2. 中國礦業大學數學學院,江蘇 徐州221116)
譜方法起源于經典的Ritz-Galerkin 方法,是一種數值求解偏微分方程的方法:譜方法最大的優點是具有“無窮階”收斂性及可采用快速算法,現已被廣泛用于氣象、物理、力學等諸多領域,成為繼差分法和有限元法之后又一種重要的數值方法。 2015 年,樊占玲[1]將兩類線性基本問題的譜方法基礎上,分別構造出一維、 二維非線性Sine-Gordon 方程的半離散與全離散格式, 最后用數值模擬驗證了該方法的有效性。 2016年,劉文杰[2]應用Chebyshev-Galerkin 譜方法離散一維半線性拋物方程的空間變量,然后使用譜配置法或塊譜配置法離散時間變量,得到了在L2權范數下的空間半離散格式的最優階誤差估計結果。2017 年,劉賀[3]用譜方法來研究一類一維空間周期型的Cahn-Hilliard 方程并證明了其收斂性。 2018 年,董帥等[4]對非線性項用Legendre 插值,在空間上用Legendre-Galerkin-Chebyshev 方法,在時間上用二階Crank-Nicolson 格式,提出Burgers 方程的廣義多項式混沌-譜方法將Burgers 方程轉化為非線性微分方程組。 基于以上各種間斷Galerkin 算子的譜性質,本文考慮真空中電磁場的Maxwell 方程問題形如下[5]
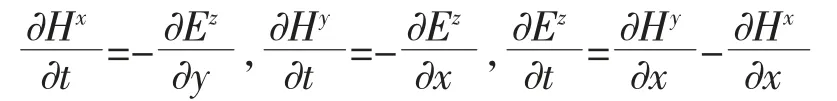
對于三維Maxwell 方程[5]

其中:E=(Ex,Ey,Ez)為電場分量,H=(Hx,Hy,Hz)為磁場分量,對應的數值通量分別為[6]
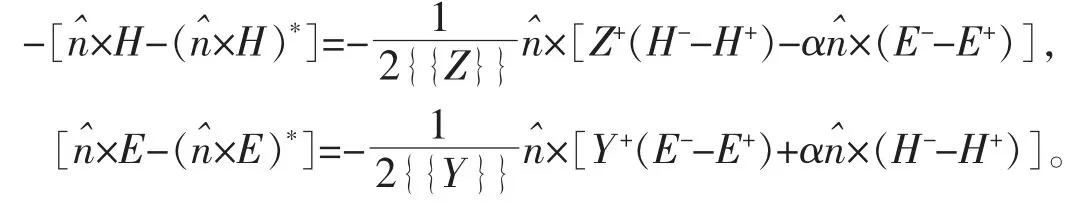

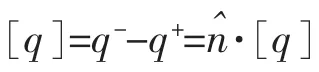
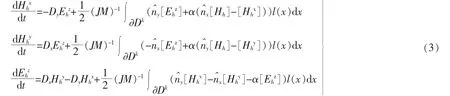
其中:(Hhx,Hhy,Ehz)為近似解。
1 局部格式
考慮Maxwell 調和形式方程

局部散度為零的條件為
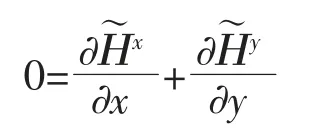
邊界條件為
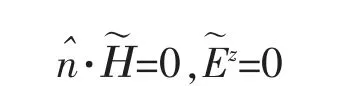
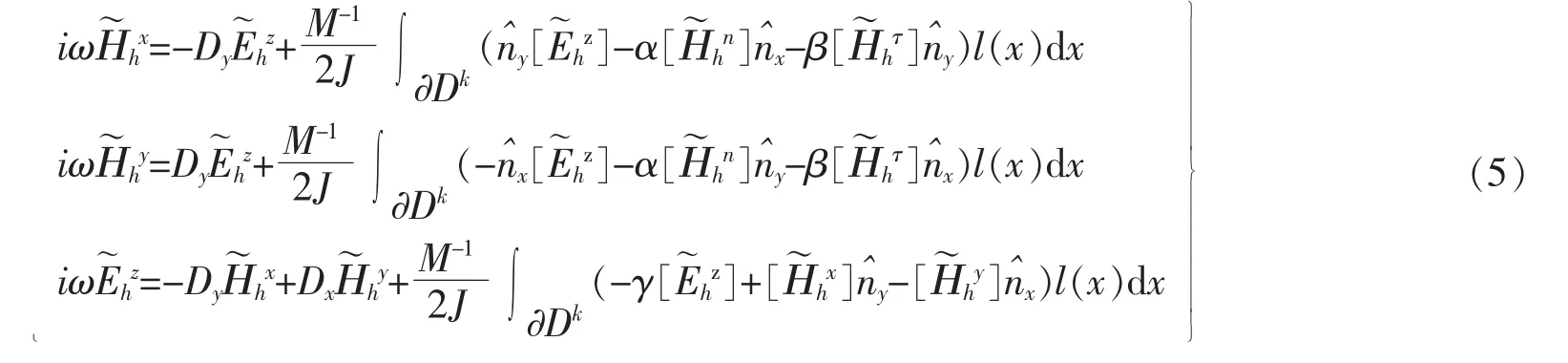
假設存在一個離散特征對ω=0,但(Hx,Hy,Hz)非零,則局部單元Lax-Fridrichs 格式為
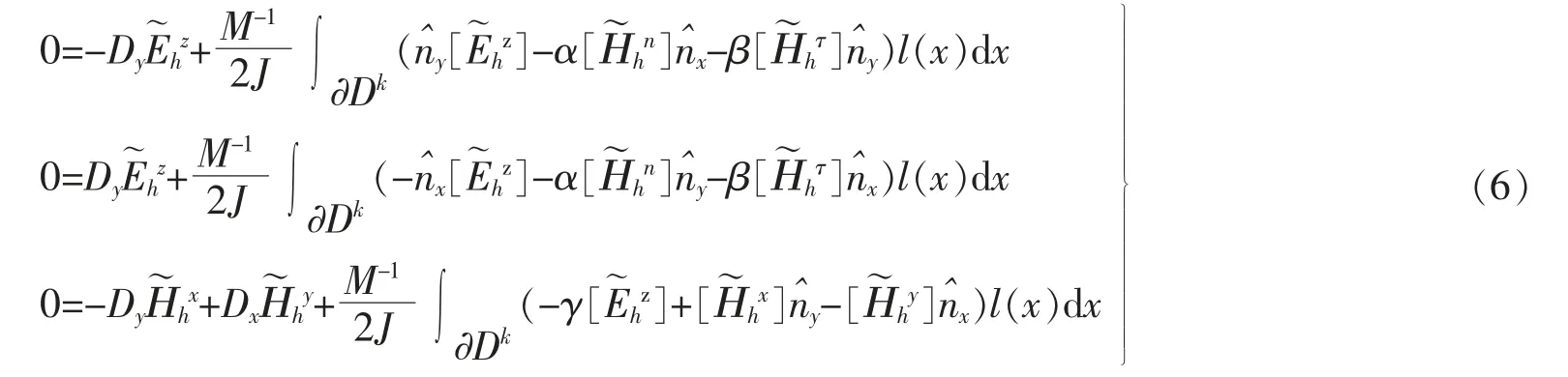
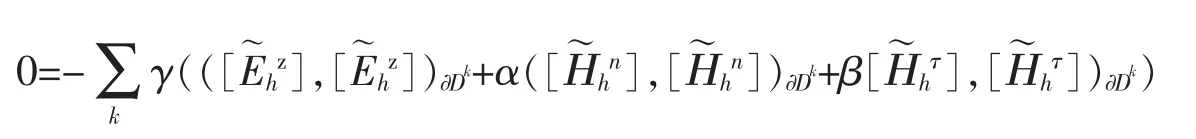
對于方程(5)格式,可以推出求解方程(4)的迎風格式[7-8]、非協調懲罰格式[9-10]、以及經 典 的Lax-Fridrichs 通量公式,由于譜方法中,測試函數通常是全局光滑的,取基函數與試驗函數相同,得到
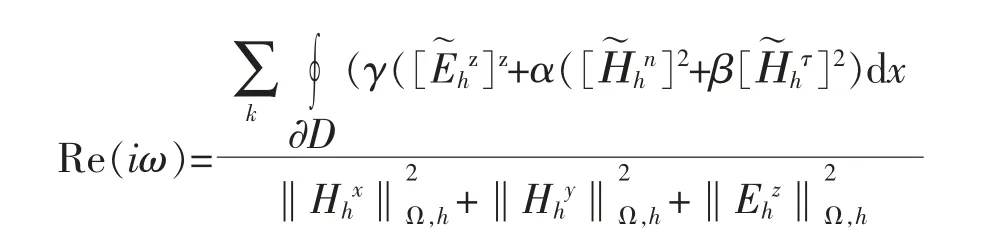
其中:α,β,γ 取任何非負數時,半離散格式L2穩定;當α=0,β=1,γ=1 時,該格式是迎風通量;當α=1,β=0,γ=1 時,該格式是懲罰通量;當α=1,β=1,γ=1 時,該格式是Lax-Fridrichs 通量。
2 數值算例
本節我們來討論Maxwell 特征值問題譜方法的實用性與有效性,考慮二維Maxwell 方程
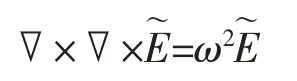
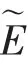
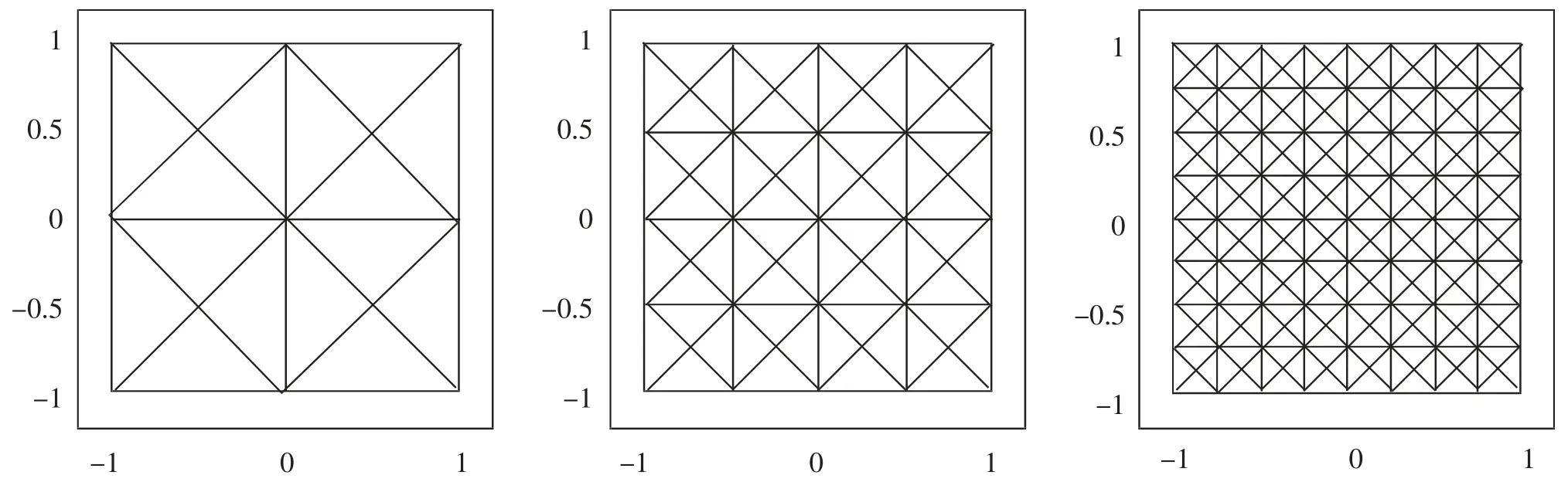
圖1 用于計算理想邊界條件金屬方塊域上特征值問題的交錯網格Fig.1 Staggered grid for calculating eigenvalue problems over metal square domains with ideal boundary conditions
下面將運用兩種不同的局部基函數,分別由迎風、懲罰和Lax-Fridrichs 通量來進行求解,一種是應用完備的N 階多項式基,另一種是不同通量結合局部散度為零的基函數。
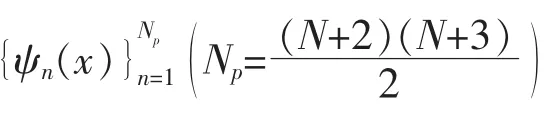
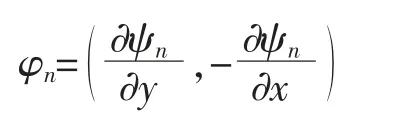
這個函數滿足▽·φn=0,將磁場表示為
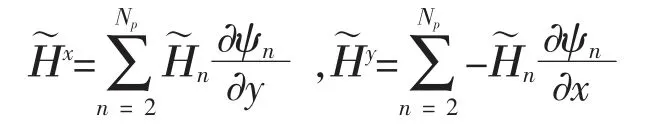
表1 給出了MATLAB 數值模擬完備多項式基N=3 與N=5 的數值結果, 可以看出該格式對方程可以達O(h2N+1)到階精度。 表2 是局部散度為零的基函數對特征值得到的收斂階,看到對N=3 收斂階O(h2N+1),而由線性算子的條件數影響N=5 的結果很不平穩。 表3 給出了懲罰通量格式完備多項式基N=3 與N=5 的數值結果,可以看出該格式對方程可以達到O(h2N-1)階精度。 表4 是局部散度為零的基函數對特征值得到的收斂階, 看到對N=3 收斂階O (h2N-1), 而由線性算子的條件數影響N=5 的結果很不平穩。 表5 給出了Lax-Fridrichs 格式完備多項式基N=3 與N=5 的數值結果,可以看出該格式對方程可以達到O(h2N+1)階精度。 表6是局部散度為零的基函數對特征值得到的收斂階,看到對N=3 收斂階O(h2N+1),而由線性算子的條件數影響N=5 的結果很不平穩。
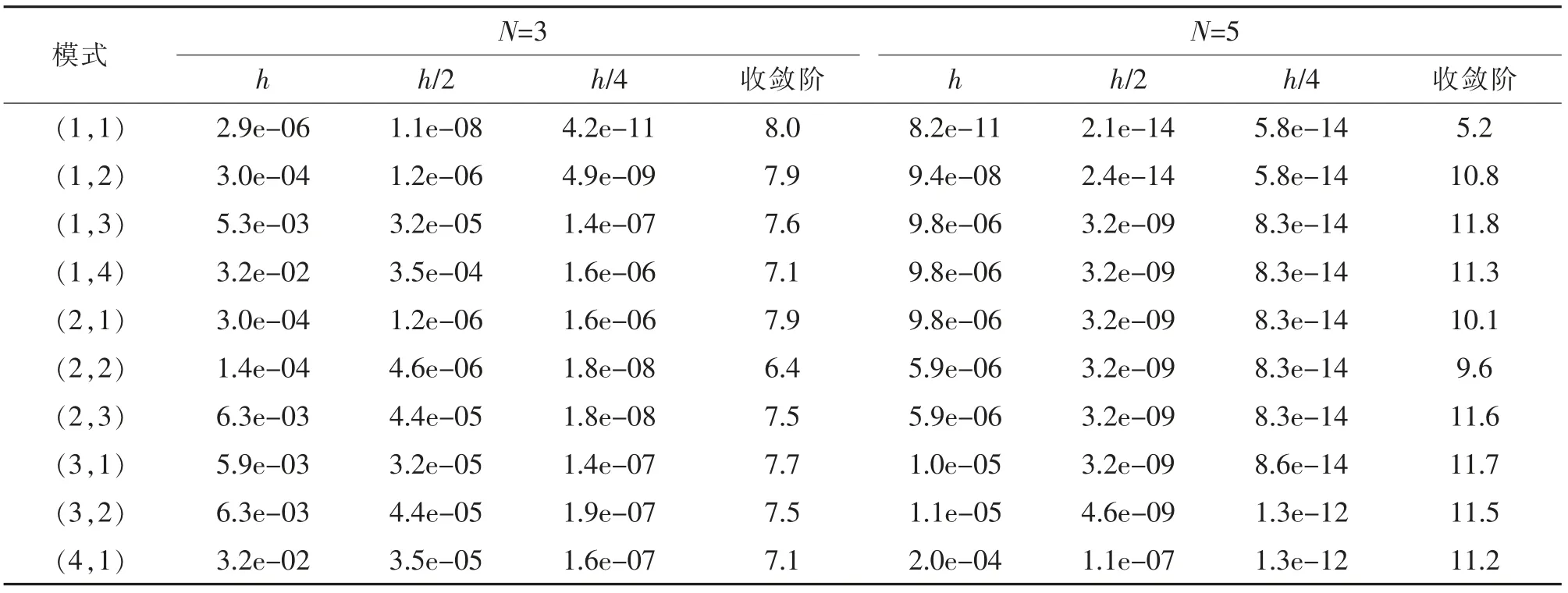
表1 具有迎風通量的前10 個特征值的收斂性Tab.1 Convergence for the first 10 eigenvalues of operator with an upwind flux
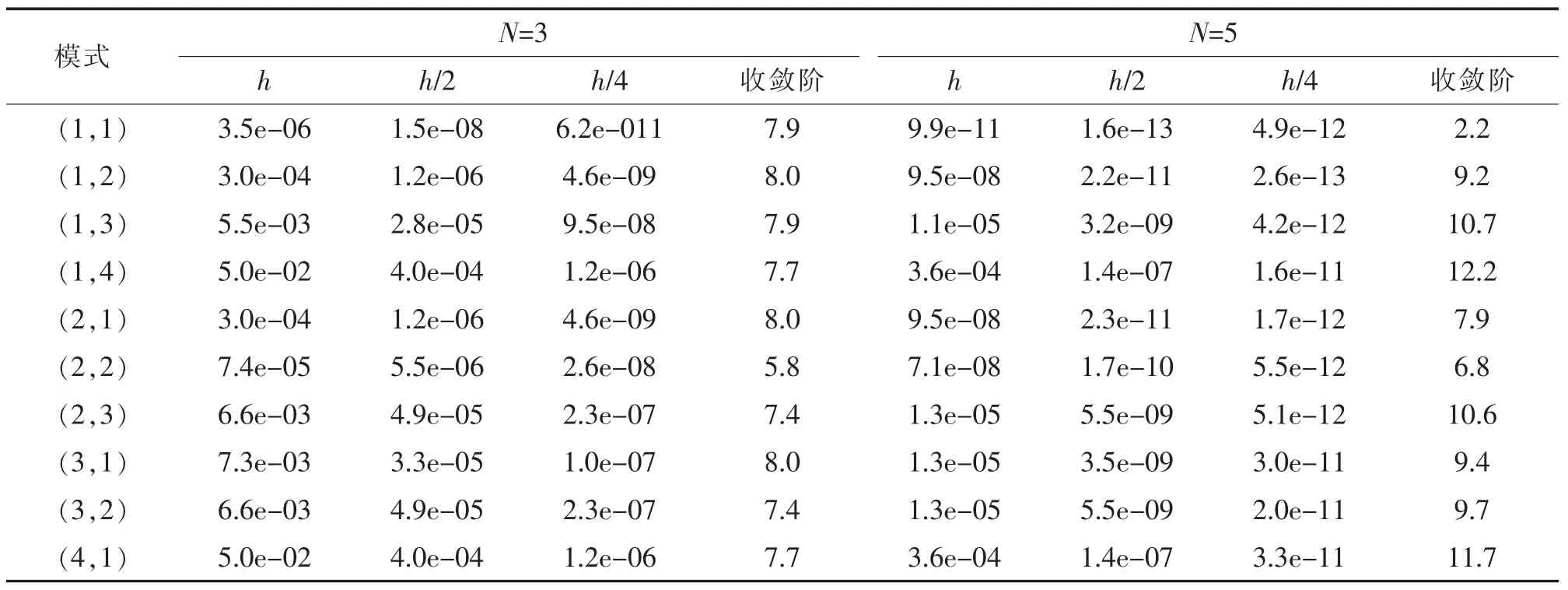
表2 局部散度為零的基對應迎風通量格式前10 個特征值的收斂性Tab.2 Convergence for the first 10 eigenvalues of operator with upwind flux and locally divergence-free basis
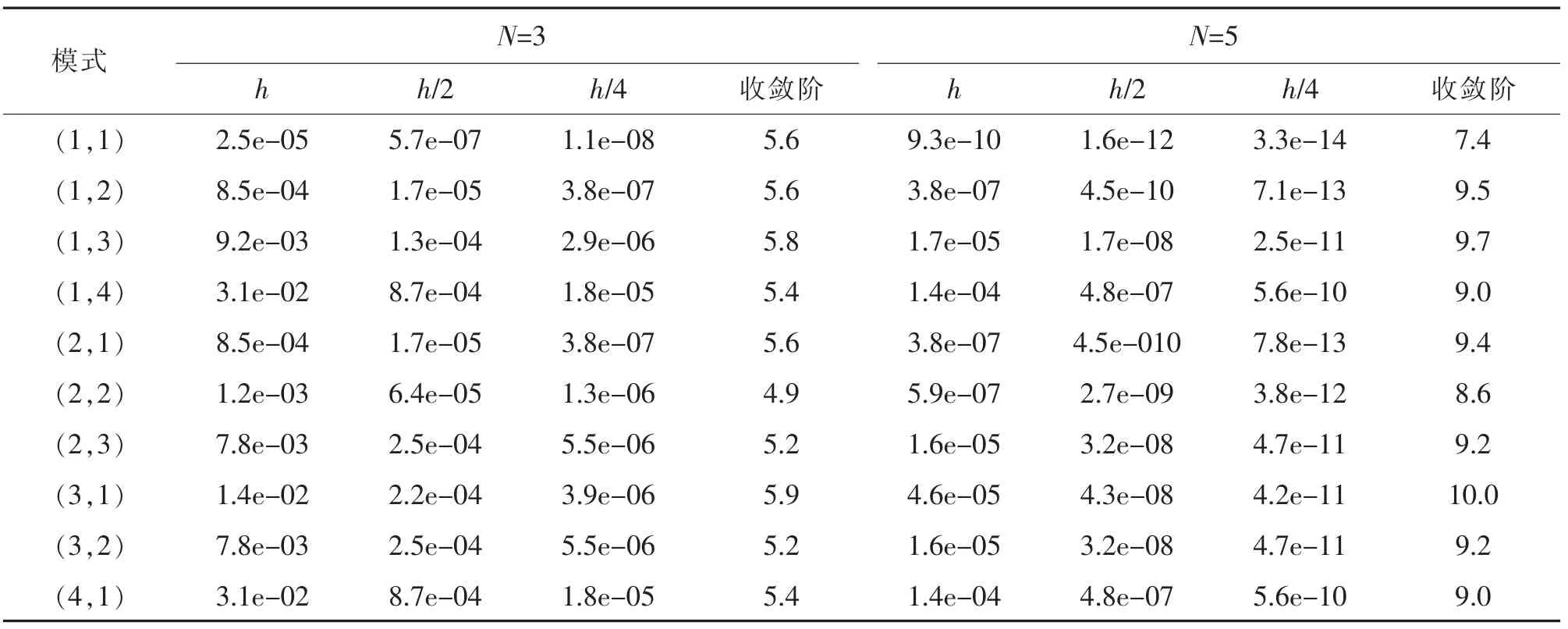
表3 具懲罰通量的前10 個特征值的收斂性Tab.3 Convergence for the first 10 eigenvalues of operator with a penalty flux
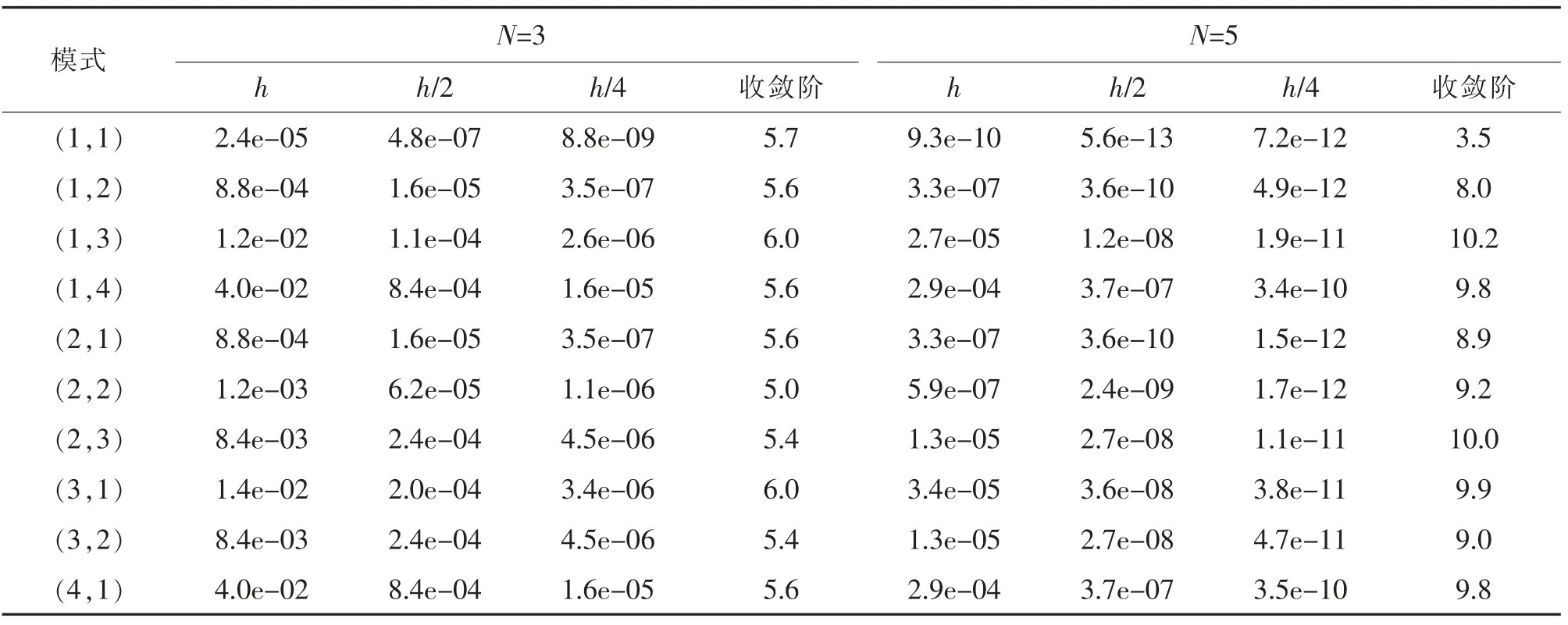
表4 局部散度為零的基對應懲罰通量格式前10 個特征值的收斂性Tab.4 Convergence for the first 10 eigenvalues of operator with penalty flux and locally divergence-free basis
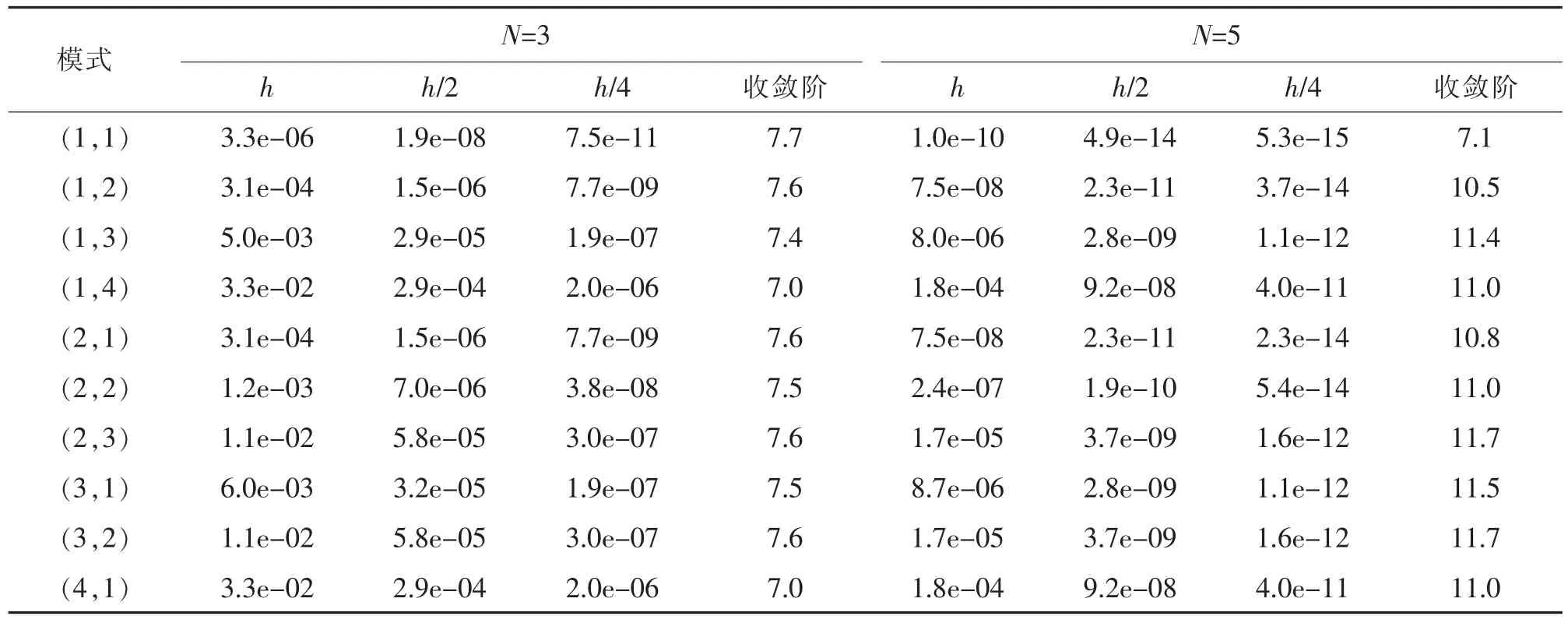
表5 具有Lax-Friedrichs 通量的前10 個特征值的收斂性Tab.5 Convergence for the first 10 eigenvalues of operator with Lax-Friedrichs flux
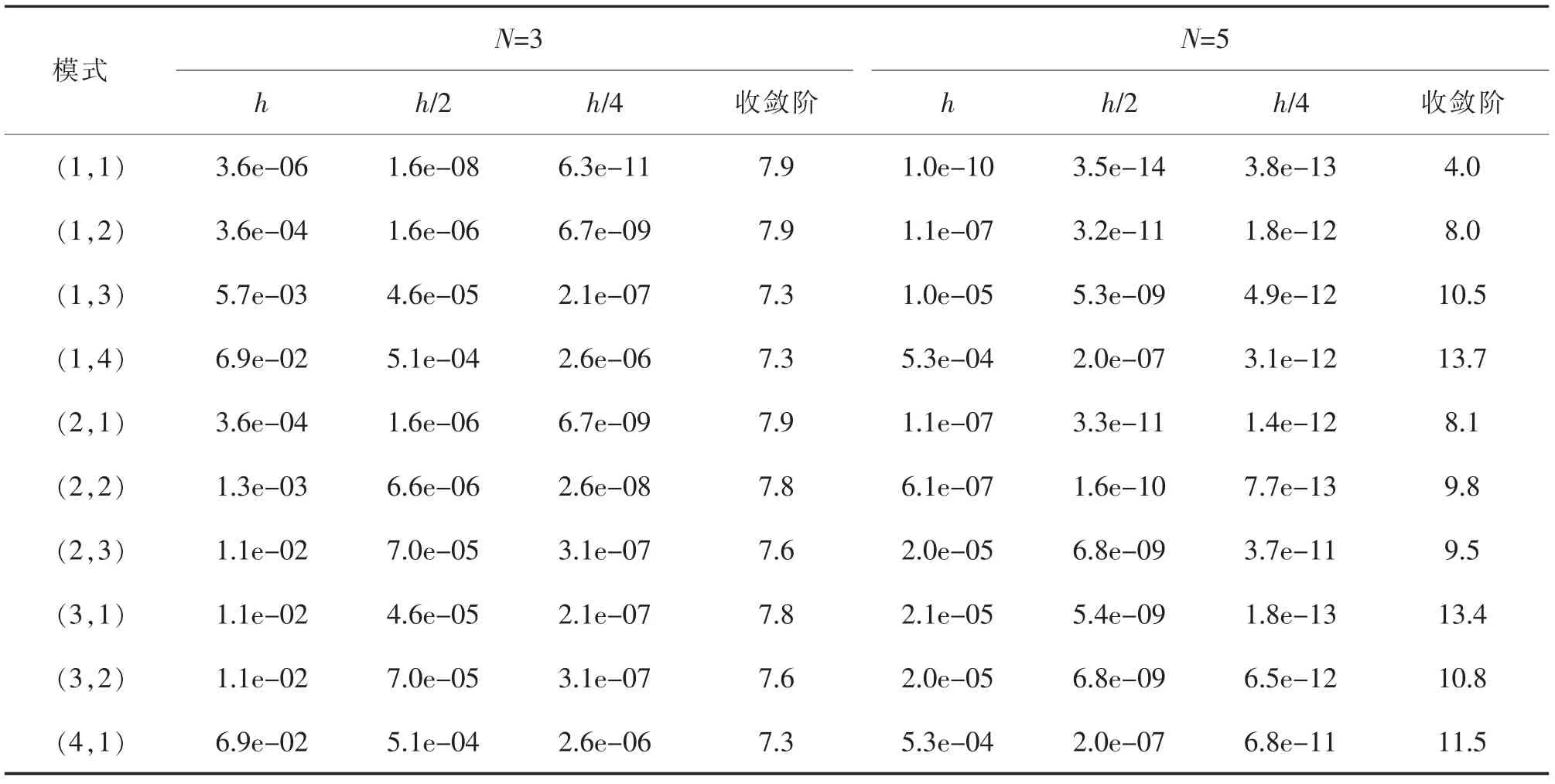
表6 局部散度為零的基對應Lax-Friedrichs 通量格式前10 個特征值的收斂性Tab.6 Convergence for the first 10 eigenvalues of operator with Lax-Friedrichs flux and locally divergence-free basis
從表1~表6 的結果可以看出,本文所運用的譜方法算法穩定可靠,所需迭代次數和計算時間雖然較大,特別迎風通量和懲罰格式互補,迎風通量用于懲罰磁場的切向分量,懲罰格式用于懲罰磁場的法向分量,但還是達到了相當好的收斂階效果。

