變載荷銑削力影響下的加工中心床身結構優化設計*

梁麗強，薩日娜,2,3*，高 峰

(1.內蒙古工業大學 機械工程學院，內蒙古 呼和浩特 010051；2.浙江大學 機械工程學院，浙江 杭州 310027；3.康力電梯股份有限公司，江蘇 蘇州 215213)

0 引 言

加工中心在現代化工業中有著廣泛的應用，床身結構作為機床重要的基礎支撐件對機床的布局有很大的影響。床身的結構尺寸和布局形式，直接影響機床的加工精度、精度穩定性和生產效率。床身設計不合理，剛度不足，會引起床身的各種變形和振動[1]。

目前，提高機床加工性能的常用方法有優化機床的結構和應用新型材料制造機床兩種[2-3]。MA Y L[4]在加工中心床身的結構優化中使用了拓撲優化的方案，完成了床身結構優化，使得床身剛度和動態性能都得到相應提高；SIGMUND O[5]針對宏觀結構、微觀結構的制造，提出了一種基于拓撲優化的延伸方法；趙二新等[6]在車削中心床鞍輕量化設計中使用了拓撲優化，實現了結構輕量化設計；崔爭爭[7]提出了針對多個目標采用加權平均的方法，把多目標優化問題轉化為單目標優化問題；張昆鵬[8]針對拓撲優化模型求解過程中，需要多次迭代才能得到滿足一定精度要求的收斂結果的問題，提出了一種基于向量Epsilon算法加速迭代序列收斂的方法；陳垂福[9]基于固體各向同性材料理論，對懸臂梁進行了拓撲優化設計，建立了懸臂梁拓撲優化數學模型，求解了位移約束下懸臂梁體積最小的拓撲結構；TENERELLI P等[10]提出了一種基于GIS的多標準、多目標和不確定性分析的方法，來評估能源作物轉換的一系列可能性；饒柳生等[11]把柔度最小和1階固有頻率最大作為目標進行了多目標優化，結合拓撲優化方法對立柱的筋板結構進行了改進；姜衡[12]在加工中心多目標優化中采用響應面法，實現了加工中心的結構優化，使其靜動態特性均得到了較好的提升；馬雅麗[13]在不確定因素影響下的機床支撐件多目標穩健性設計中，通過靈敏度法和支持向量機方法，實現了機床支撐件的結構優化設計。

對于銑削加工時，考慮銑削加工過程中銑削力隨時間變化的變載荷對床身結構優化的影響；同時當模型外形較復雜結構尺寸較大時，都對有限元優化求解的效率產生了不利的影響。所以本文針對加工中心床身的結構優化過程合理地定義了拓撲優化的變載荷施加；在多目標尺寸優化過程中將床身拆解成小的單元結構來完成床身的尺寸優化，既可以減少計算的求解時間，又能有效地完成模型的優化設計。

針對以上問題，本文對床身進行多目標優化，使床身結構更加合理有效。

1 加工中心床身結構拓撲優化

1.1 加工過程中變載荷切削力及工況分析

筆者主要對加工中心銑削加工時動態銑削力對床身結構優化的影響加以研究。

以加工中心進行銑削加工為例，銑刀為圓柱形銑刀，根據銑削公式[14]，有：

(1)

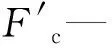
(2)

式中：Ff—縱向進給力；Fe—橫向進給力；Ffn—垂直進給力。

計算得到Ff=1 000 N,Ffn=1 100 N,Fe=1 400 N。切削是一種周期性切削過程，其周期為刀具旋轉一周的耗時[16]。

以周期為0.15 s，銑削力隨時間周期變化的規律及銑削力的傳遞路徑，如圖1所示。

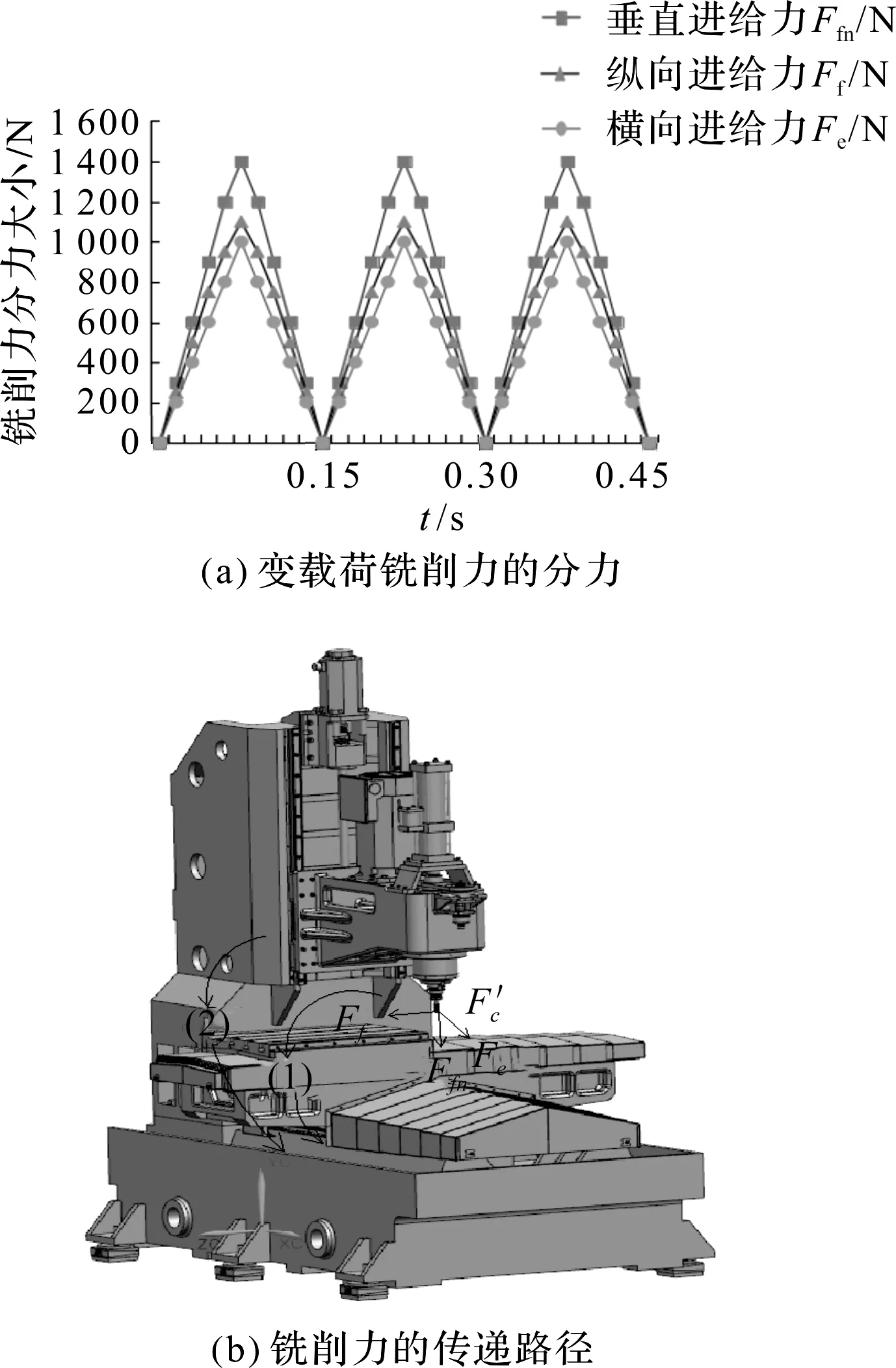
圖1 變載荷銑削力分力及其傳遞路徑

加工中心銑削加工時，按照工作臺的不同位置來劃分加工中心的不同工況，如圖2所示。

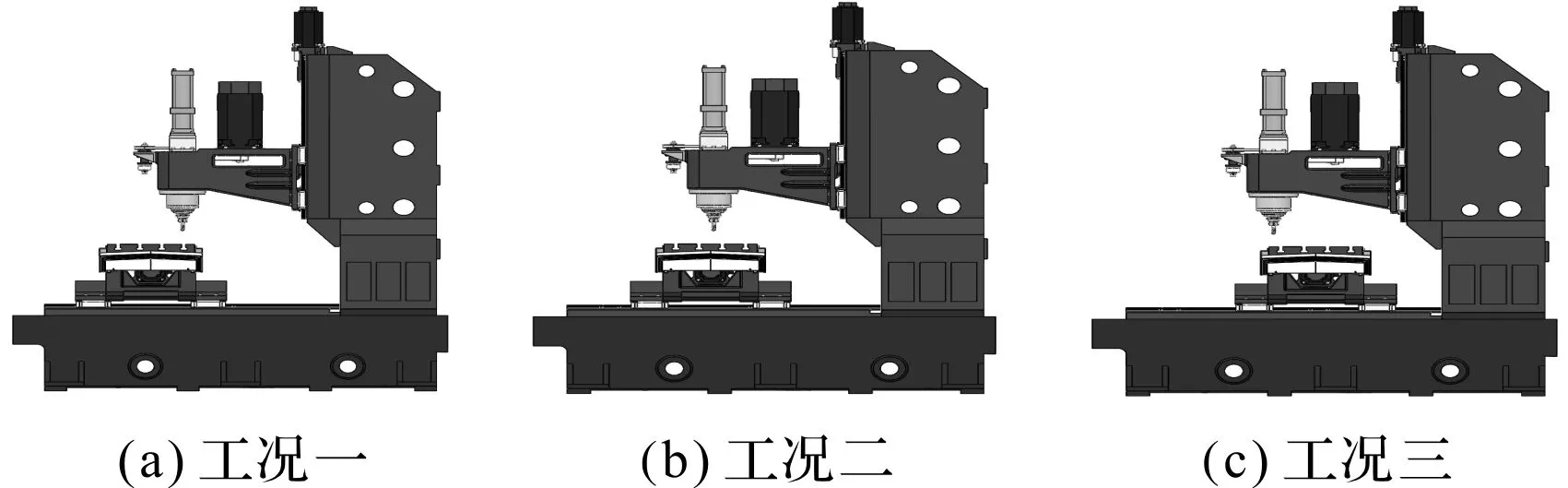
圖2 加工中心工況分析

圖2中，工況一：工作臺位于導軌的左端的極限位置；工況二：工作臺位于導軌中間位置；工況三：工作臺位于導軌右側極限位置。

1.2 加工中心床身變載荷拓撲優化數學模型

鑒于SIMP算法具有較好的收斂性和應用價值，筆者選擇SIMP模型變密度法，對機床底座進行優化設計[17-18]。

在結構優化中，通常將剛度目標函數轉化為柔度目標函數進行求解，柔度可以通過結構的應變能來表示：

(3)

式中：Ci—第i個工況下，床身結構柔度；Fi—第i個工況下，有限單元節點載荷向量；Ui—第i個工況下，有限單元節點位移向量；Vi(x)—拓撲優化后，床身結構體積；V0—原始體積；f—體積分數約束取值為0～1。

因此，通過折衷規劃法得到結構柔度最小[19]的目標函數為：

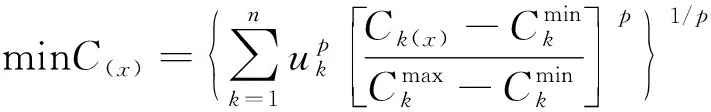
(4)

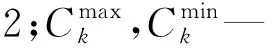
以低階固有頻率最大為目標的拓撲優化中，會遇到當某一階固有頻率達到最大值時，而其他階固有頻率下降到了很小的值，優化結果難以滿足設計要求[20]。因此，在低階固有頻率的優化時，需要綜合考慮多階頻率，即：

(5)

式中：Λ(x)—頻率的平均數；z0,k—調整目標函數的參數；f—所優化的頻率階數；ωi—頻率權值；λi—第i階特征頻率。

同時，考慮結構柔度和固有頻率的多目標拓撲優化目標函數，變量xi來表示i單元相對密度ρi，可得到多目標拓撲優化的綜合目標函數:

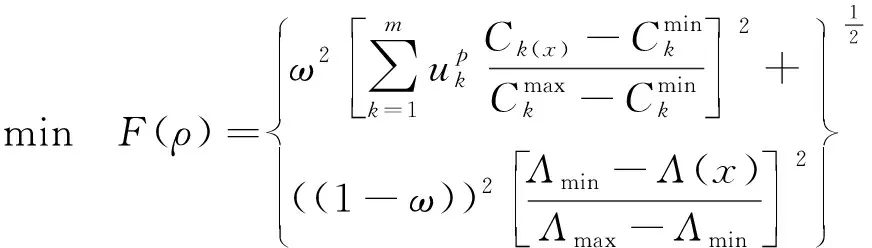
(6)

式中：xi—優化設計變量，代表離散材料單元i的相對密度，取值為[xmin，1]之間的連續值；ω—柔度目標函數的權值；1-ω—固有頻率目標函數的權值；Λmax，Λmin—平均頻率的最大值、最小值；Vi—拓撲優化結果的結構體積；V0—結構優化前體積；fv0—拓撲優化允許的體積上限值。

為了有效避免總剛度矩陣出現的奇異現象，取Xmin=0.001。

1.3 加工中心床身的拓撲優化設計

1.3.1 加工中心床身有限元模型的建立

床身的三維模型和有限元模型如圖3所示。

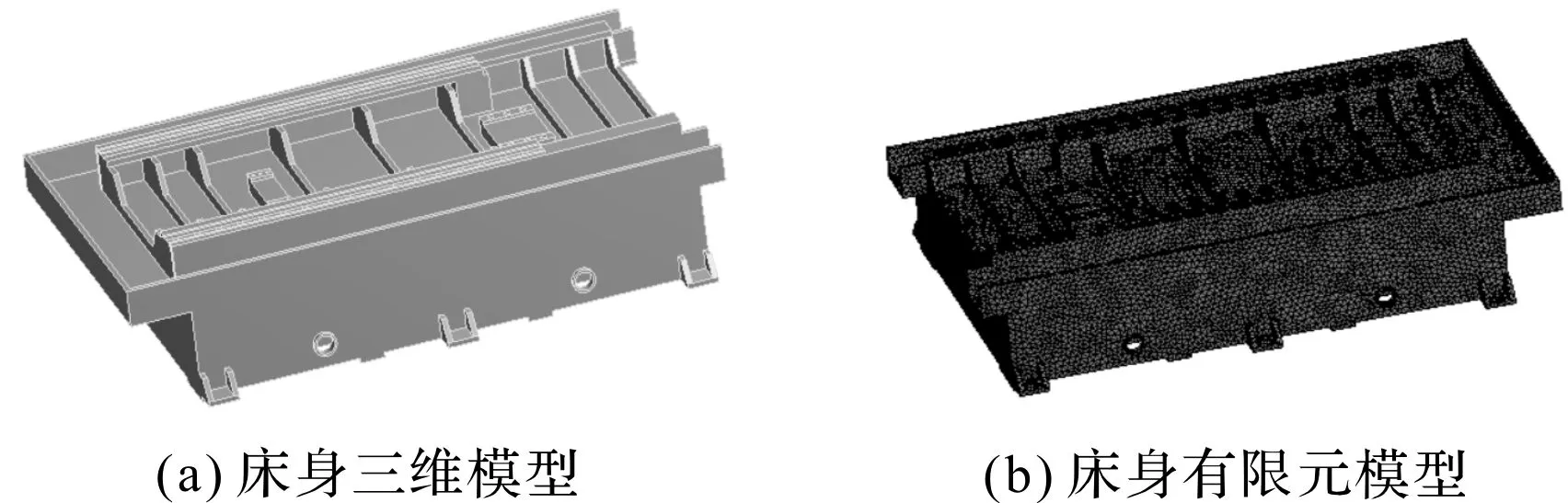
圖3 床身模型

圖3中，床身的材料為HT200，彈性模量為148 GPa，泊松比為0.26，密度為7 200 kg/m3，床身質量為993.7 kg；床身長1 968 mm，寬1 290 mm，高456 mm，壁厚16 mm；床身內部設計有不同位置的加強筋厚度為16 mm，筋板與外壁均設計有出砂孔。

采用Workbench網格劃分技術，對加工中心床身模型進行網格劃分，共得到312 611節點和164 870個單元。

1.3.2 加工中心床身的載荷與約束條件

床身主要受兩部分力的作用，一部分是銑削力的作用，另一部分是安裝在床身上的立柱、刀庫、主軸組件、工作臺等部件的壓力。

將銑削力按照周期為0.15 s,加載到加工中心床身上。將銑削力沿著加工中心工作臺的運動方向進行分解，縱向進給力垂直作用于導軌側面,其值為2 200 N，垂直進給力方向為垂直于兩導軌，其值為2 800 N,以及滑座和加工工件總質量420 kg，橫向進給力沿導軌方向其值為2 000 N，以及床身上的立柱、刀庫、主軸組件、工作臺總質量施加給床身的力。

床身的載荷和約束如圖4所示。

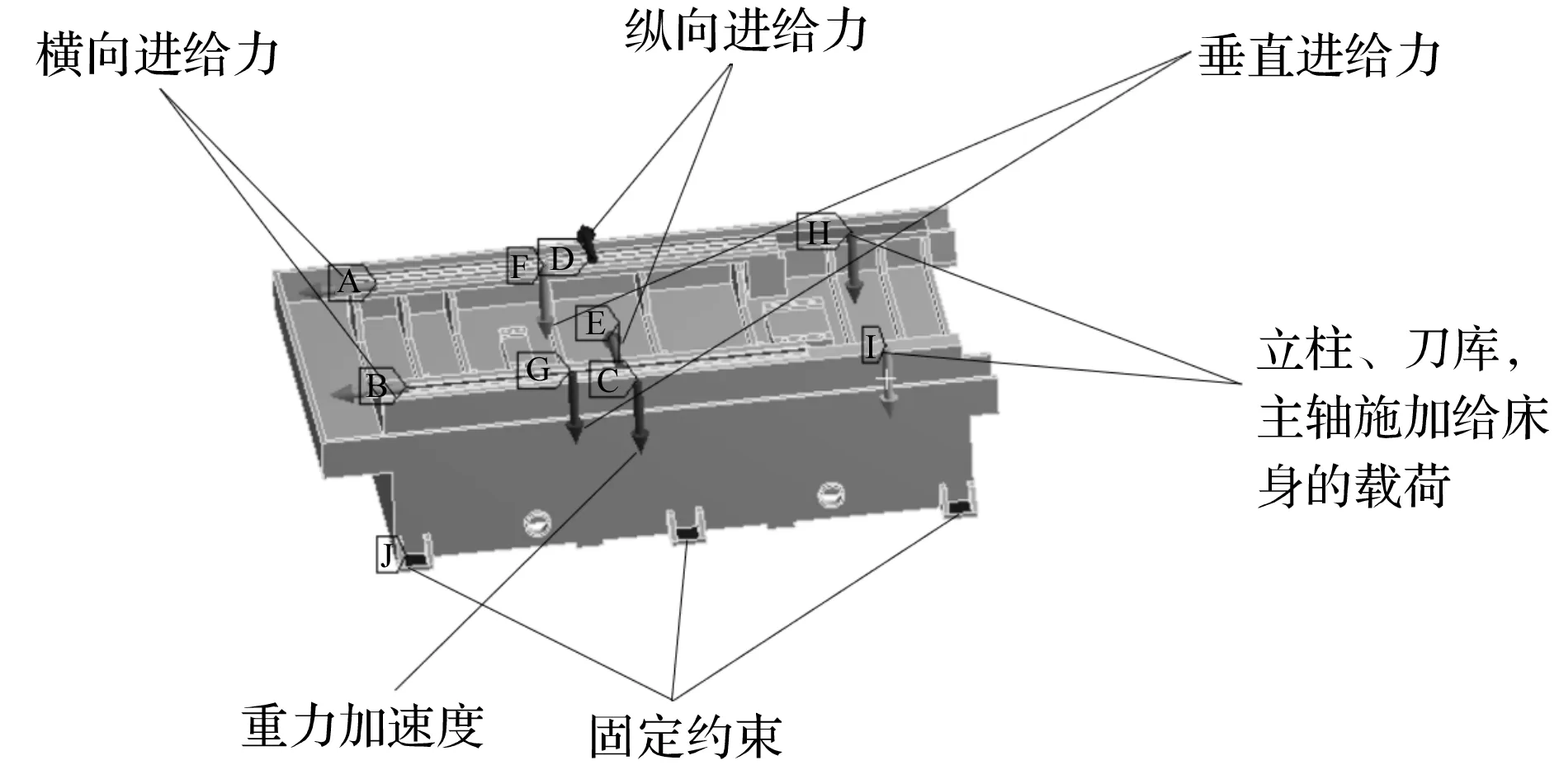
圖4 床身載荷與約束

床身是由底部的6個螺栓與地面固定，所以筆者對6個螺栓孔施加完全約束。橫向進給力施加于床身導軌沿X軸正方向，縱向進給力作用在導軌側面沿Y軸正方向，垂直進給力施加于垂直導軌沿Z軸正方向，以及床身上的立柱、刀庫、主軸組件、工作臺總質量施加給床身的力沿Z軸正方向。

筆者基于Workbench中Topology Optimization模塊，對床身有限元模型進行拓撲優化[21-22]。

在Workbench中，筆者對加工中心床身模型進行約束設置，體積分數設置為0.7～0.8，定義設計區域與非設計區域。優化以提高動態特性為主，故選取綜合目標函數式中固有頻率項的權值為0.6，柔度項權值為0.4。

拓撲優化目標及權重設定如表1所示。

表1 拓撲優化目標及權重設定

在保證床身前三階固有頻率和柔度的情況下，得到結構的最佳材料分布。

在Topology Opitimization求解器中，對設計空間進行分析。

設計空間穩定之后，床身得出的拓撲形態以及拓撲優化目標函數的迭代過程，如圖5所示。

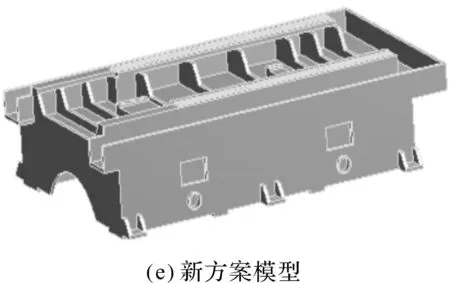
圖5 拓撲優化形態及其迭代過程(a)—拓撲優化收斂穩定后的拓撲形態；(b)—前三階固有頻率迭代過程；(c)—拓撲優化過程中床身體積迭代過程；(d)—多目標拓撲優化綜合函數經過45次迭代收斂過程；(e)—根據床身結構拓撲優化結果，建立了新的床身方案模型

1.3.3 加工中心床身新方案性能評估

新的床身方案模型按照拓撲優化模型指導的去除率進行建模，去除了多余的筋板并且在床身的前后位置以及側面進行開孔設計。

將床身的新舊模型進行分析對比，其性能參數對比如表2所示。

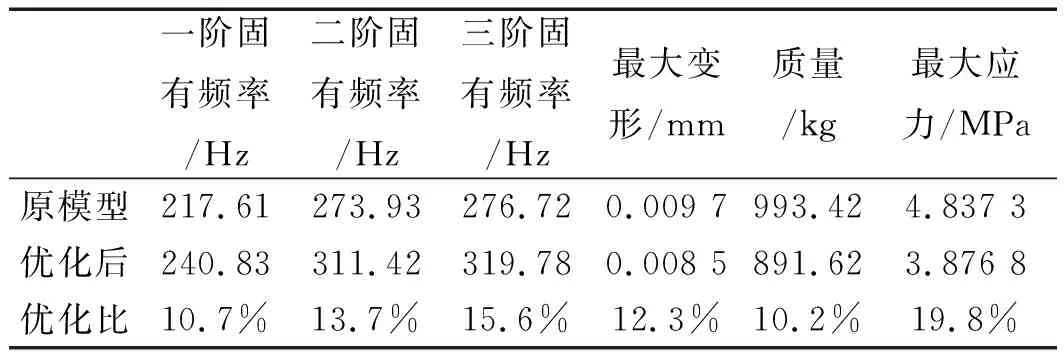
表2 優化前后床身性能參數對比

2 床身結構單元多目標尺寸優化

響應面分析作為尺寸優化的一種有效方法，其可以在繼承多目標拓撲優化的基礎上，進一步完成加工中心尺寸優化。

將床身整體結構拆分成小基本單元結構，進行響應面分析，既可以減少計算的求解時間，又能有效地完成模型的優化設計。

基本單元結構如圖6所示。

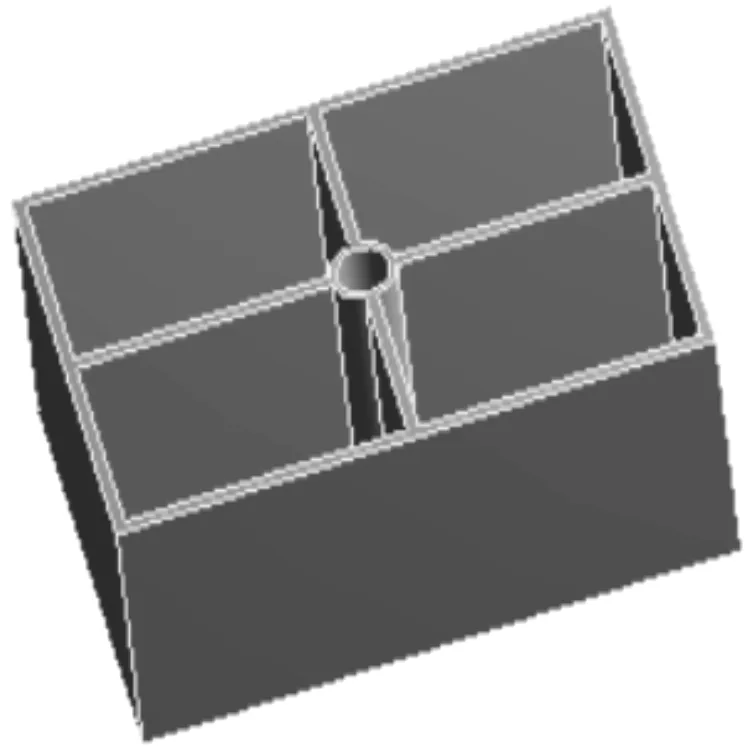
圖6 基本單元結構結構

筆者定義了5個設計變量和兩個目標函數，分別為P1單元壁厚、P2單元拉伸高度、P3單元筋板厚度、P4單元長度、P5單元寬度。目標函數為P6單元固有頻率、P7單元質量。

為了構建標準二階響應面模型，筆者首先對定義的5個設計變量進行靈敏度分析[23]，如圖7所示。

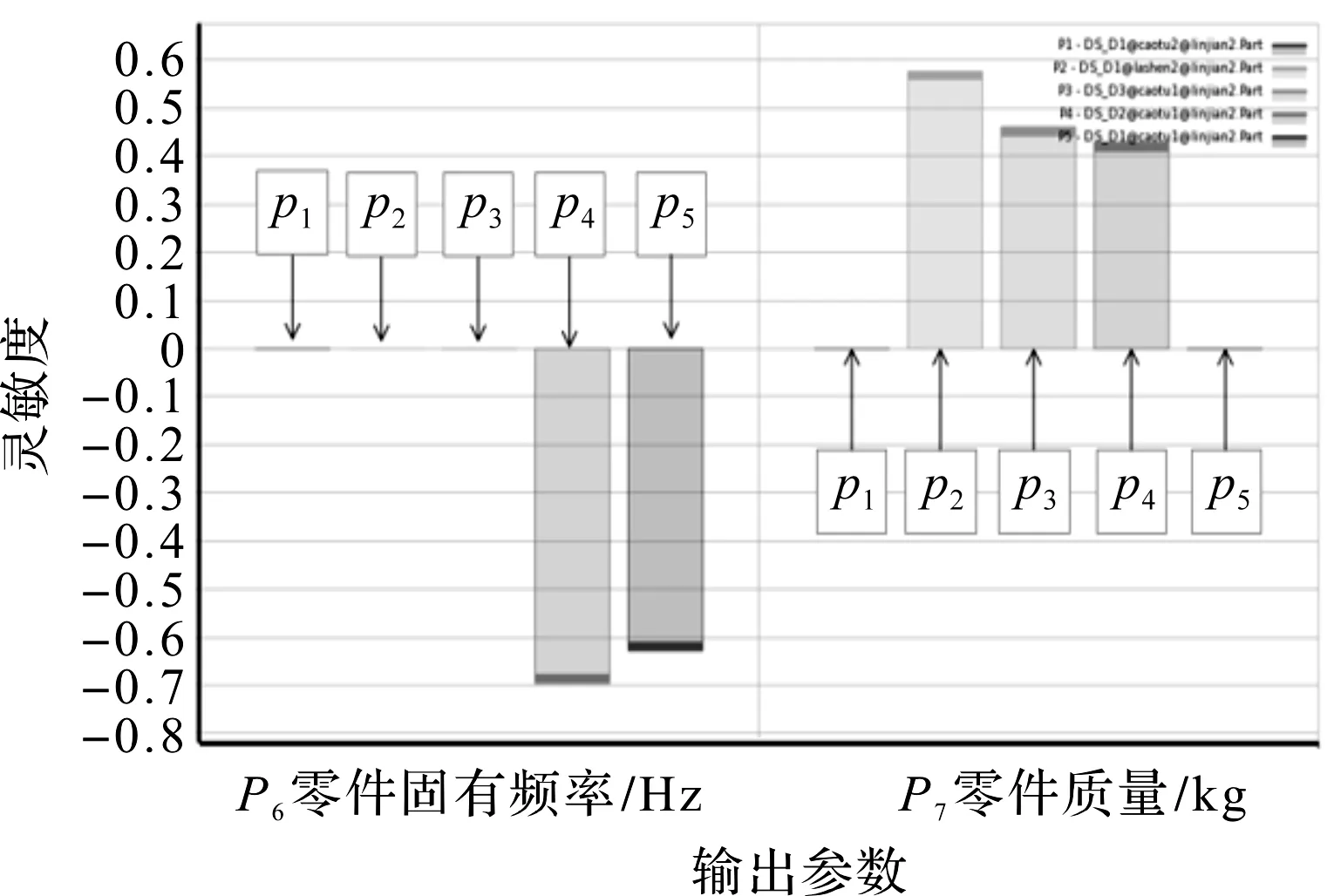
圖7 靈敏度分析圖

由靈敏度分析圖可以看出，P1設計變量對單元的兩個目標函數影響較小，予以剔除。故將其與4個設計變量作為構造響應面優化的設計變量。

然后采用Optimal Space-Filling Design最佳填充空間設計方法，在樣本空間生成25個樣本點，如表3所示。

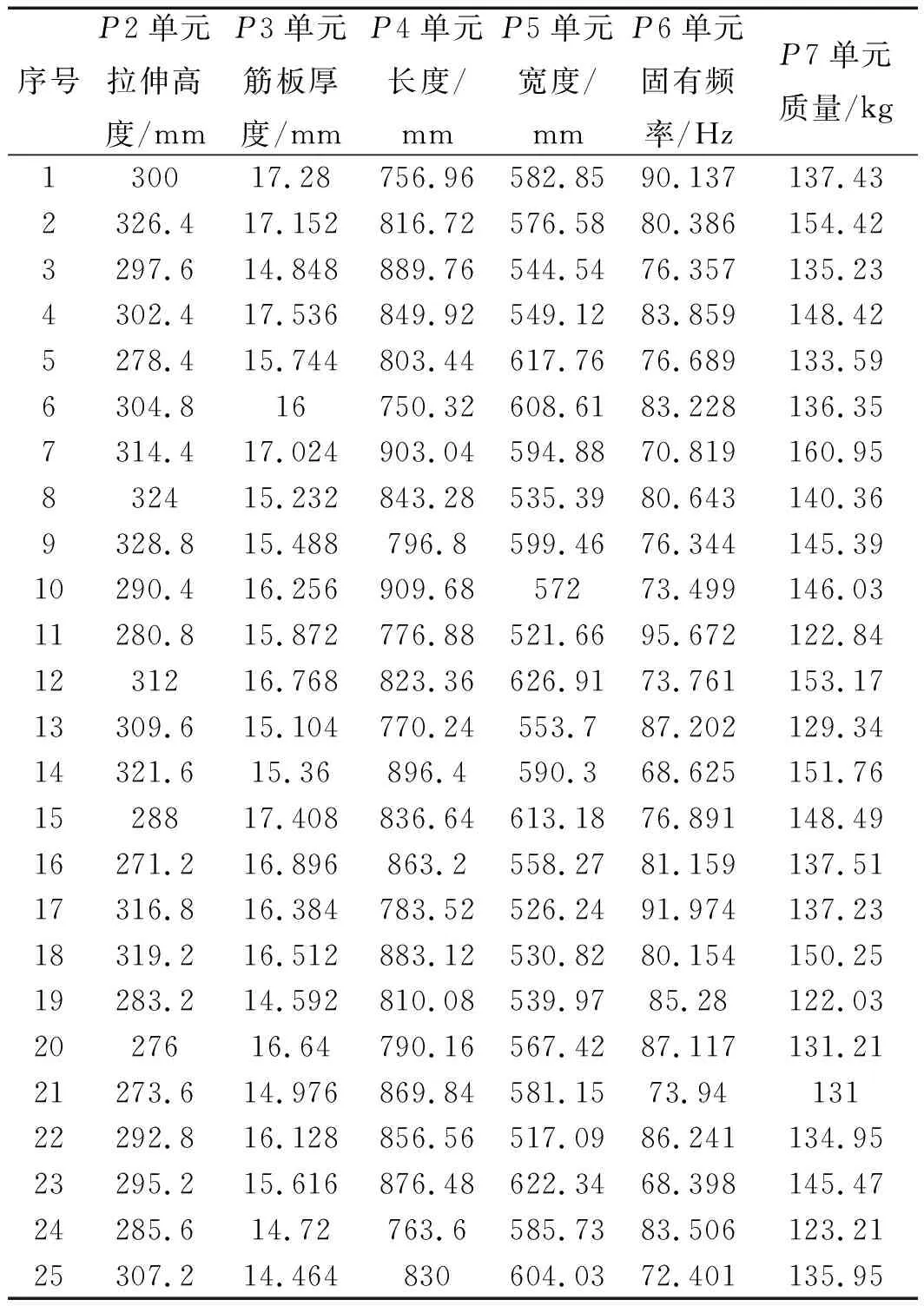
表3 抽樣所生成的空間樣本點

通過Workbench更新計算，得到樣本點對應的響應值。

將樣本數據導入response surface中，進行響應面模型的構建，如圖8所示。

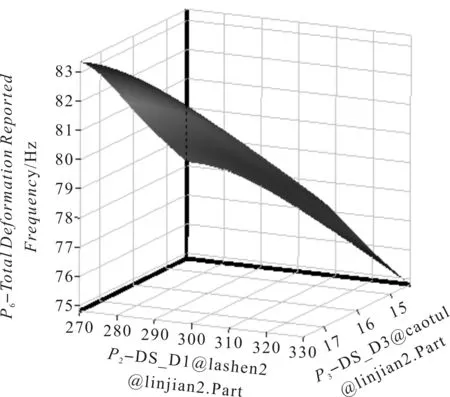
圖8 結構單元響應面模型

響應面優化結果的有效與否受其擬合精度影響，故對響應面的擬合精度進行評估，如表4所示。

表4 響應面擬合精度

表4中，給出了響應面模型擬合精度；其中，P6和P7分別表示單元一階模態頻率總質量和一階模態頻率。可知該響應面模型精度滿足要求，可用于后續的多目標優化求解。

在Workbench中，基于床身質量和一階固有頻率建立的響應面模型，采用MOGA優化算法進行優化求解，其優化算法求解參數設置如表5所示。

表5 MOGA優化參數設置

最終優化得到的3組候選點如表6所示。

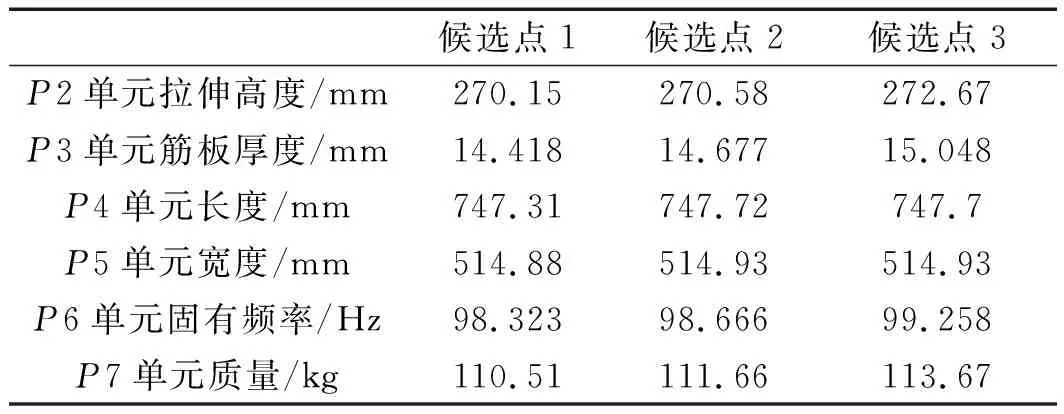
表6 優化后的候選點

3組候選點的擬合精度都符合實驗設計精度要求，因此，將第3組候選點作為最終優化方案。

將第3組候選點方案與原模型進行比較，如表7所示。

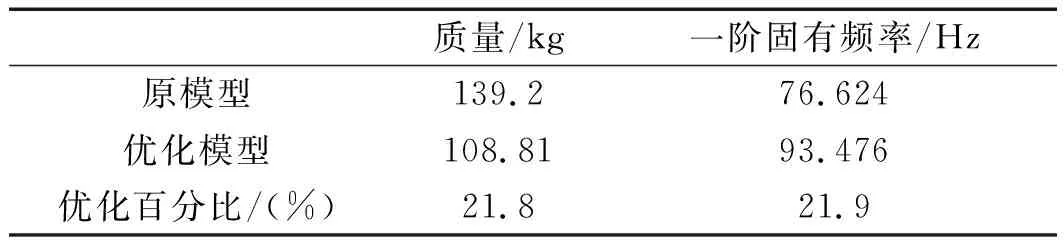
表7 優化方案與原模型性能參數對比

由表7中可以看出：結構單元的一階固有頻率優化了21.9%，質量減少了21.8%。

3 優化結果性能分析及對比驗證

3.1 優化結果性能分析

將響應面優化后的單元結構尺寸代入床身模型中，對比優化后床身模型與原模型以及拓撲優化模型，如表8所示。

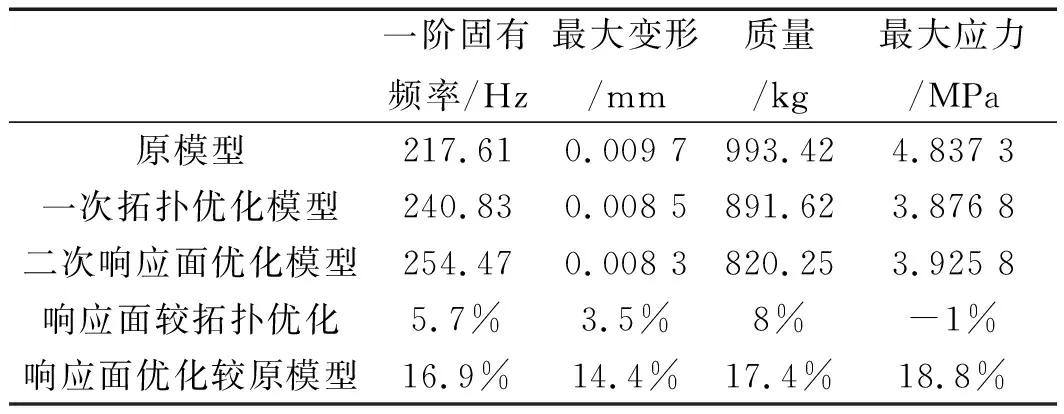
表8 優化后結構性能參數對比

3.2 對比驗證

基于Ansys有限元分析軟件，筆者實現了加工中心床身的多目標拓撲優化以及結構尺寸優化。

為驗證結果的有效性，故將優化結果與Hyper Works有限元分析結果進行對比，如圖9所示。

圖9 對比驗證

從圖9中可以看出：其拓撲優化后的材料保留基本一致；比較其相關結構性能參數可知，采用本文方案得到的最終優化結果較hyperworks優化結果在結構性能方面都有不同程度的提高，證明了本文采用的優化方案是合理有效的。

4 結束語

本文針對加工中心工作過程中變載荷銑削力對床身結構性能的影響問題，提出了以床身固有頻率和柔度為目標，體積分數為約束條件的多目標拓撲優化設計方法；從床身整體方面，采用折中規劃法和平均頻率法，構建了變載荷銑削力影響下的多目標拓撲優化的數學模型；依據變密度法拓撲優化，獲得了加工中心床身的最佳結構布局；在此基礎上，從床身結構單元方面借助經過優化的拉丁超立方采樣，構造了單元標準二階響應面,使用多目標遺傳算法對床身進行多目標尺寸優化。

優化結果表明：床身固有頻率增加16.9%，床身質量減少17.4%，最大變形量降低14.4%，最大應力降低18.8%。

該優化方案使加工中心床身的結構布局更加合理，實現了輕量化設計，有效地提高了床身的各項力學性能，并且有較高的設計效率。

對于床身的多目標結構優化時，關于目標函數權重的選取具有一定的經驗成分，筆者的下一步工作將針對多目標函數的不同權重系數，對結構優化產生的影響進行研究。