由“箏形”引發(fā)的探究之旅

陳建

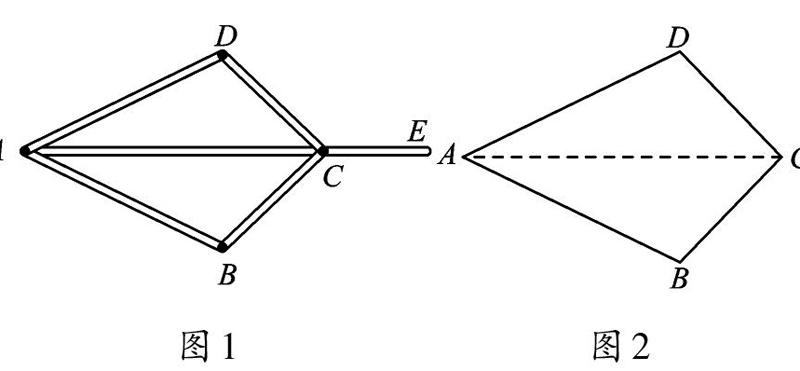
暑假期間，小明用5根木棒制作了如圖1所示的模型。其中，AD 的長與AB 的長相等，BC 的長與DC 的長相等，并分別用可旋轉(zhuǎn)的螺絲連接，木棒BC 與DC 的連接處C可在木棒AE 上滑動。小明發(fā)現(xiàn)：當C 在可滑動范圍內(nèi)滑動時，∠B 與∠D 的度數(shù)始終相等。這是為什么呢？小明百思不得其解。開學后小明學習“全等三角形”，突然有了靈感：這不就是全等三角形問題嗎？

這個問題可以用數(shù)學語言表達：

小明想，∠B 和∠D 分別在△ABC 和△ADC 中，只需證明這兩個三角形全等即可。而AB=AD，CB=CD，AC 又是公共邊，顯然可用“SSS”證明全等。

小明又琢磨，如果沒有AE 這根木棒，∠B 與∠D 還相等嗎？他想到，要證角相等，還是要借助三角形。于是，他連接AC，居然和上面問題完全一樣。此時，小明由此得到啟發(fā)：在證明兩個三角形全等時，一定要注意隱藏條件，如公共邊、公共角、對頂角，有時要學會構(gòu)造，如構(gòu)造公共邊，這是證明全等三角形時常用的一種輔助線。

這種兩組鄰邊分別相等的四邊形和風箏的形狀相似，小明覺得這個模型非常神奇，于是他上網(wǎng)搜索。他發(fā)現(xiàn)，原來，人們把具備這種特征的四邊形稱為“箏形”。“箏形”不僅簡潔、美觀，而且還有許多性質(zhì)。

性質(zhì)1 “ 箏形”具有一組對角相等（∠B=∠D）。

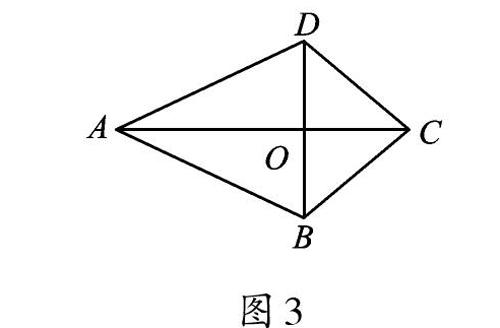
性質(zhì)2 “箏形”的一條對角線平分一組對角（如圖3，∠BCA=∠DCA，∠BAC=∠DAC）。

性質(zhì)3 “箏形”的兩條對角線互相垂直，面積等于兩條對角線積的一半（如圖3，AC⊥BD，S 四邊形ABCD=12AC·BD）。

小明發(fā)現(xiàn)，性質(zhì)1、性質(zhì)2 可以通過△ABC≌△ADC 得到，對于性質(zhì)3的證明，可以用數(shù)學語言表達如下：

已知，如圖3，AB=AD，CB=CD，對角線BD 與AC 交于點O，若AC=8，BD=6，求四邊形ABCD 的面積

小明想，“箏形”沒有面積計算公式，需要把“箏形”轉(zhuǎn)化為熟悉的圖形來求面積。對角線AC 把“箏形”分割成△ABC 和△ADC，那么我們便可以計算兩個三角形的面積，于是解題關(guān)鍵就是找出AC 邊上的高。因為△ABC≌△ADC ，所以∠BCO= ∠DCO 。在△BCO 和△DCO 中，可以利用“SAS”證明全等，所以∠BOC=∠DOC=90°，即AC⊥BD，所以S四邊形ABCD=S△ABC+S△ADC=12AC·OB+12AC·OD=12AC·（OB+OD）=12AC·BD=24。

小明運用轉(zhuǎn)化的思想方法，將“箏形”問題轉(zhuǎn)化為三角形問題，從而得出“箏形”面積的計算方法。轉(zhuǎn)化是我們解題中常用的思想方法。其實，只要是對角線互相垂直的四邊形，其面積都等于對角線長度的積的一半。

利用“箏形”的性質(zhì)，可以解決許多問題，我們來看兩道例題。

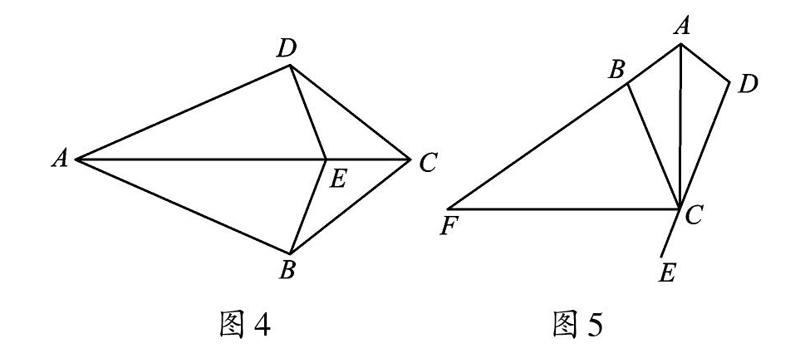
例1 如圖4，AB=AD，CB=CD，點E 是AC 上一點，連接BE、DE，試說明BE=DE。

【解析】只需證明△BCE 與△DCE 全等或證明△ABE 與△ADE 全等。因為△ABC≌△ADC，所以∠BCE=∠DCE，所以在△BCE 和△DCE 中，可以利用“SAS”證明全等。

例2 如圖5，AB=AD，CB=CD，∠BAD=100°，四邊形ABCD 的外角平分線CF 與AB的延長線交于點F，求∠F。

【解析】由性質(zhì)2可知CA 平分∠BCD，又CF 平分∠BCE，∠BCD 和∠BCE 互為鄰補角，所以易得∠ACF=90°，這是求∠F 的關(guān)鍵。所以∠F=180°-∠ACF -∠BAC=40°。

我們在解決選擇題和填空題時，運用“箏形”的性質(zhì)可以節(jié)省不少時間。當然，這只能算是“小明定理”，在解答題中必須要給出證明步驟。