多路信號的抗混疊濾波器設計

宋金玲 姜 蘇 杜鐘祥 席紀江 陳善恒 王洪梅

（1、中國礦業大學 信息與控制工程學院，江蘇 徐州221116 2、徐州市第一人民醫院，江蘇 徐州221117）

軟件無線電在應用中，往往需要同時處理不同頻帶上的多個射頻信號，選擇合適的采樣頻率是接收多頻帶信號的一個難點。大多數學者在處理多頻段信號時，為了降低接收機后端對數字處理方面的負擔，在信號頻譜不混疊的前提下，盡量選取低采樣頻率。然而為了避免信號混疊，學者們致力于研究頻率選擇算法，這樣做不僅加大了計算的繁瑣程度，還在防止信號頻率混疊方面限制了頻率選擇。另外采樣精度會隨著對信號采樣頻率要求越低而使得對RF 帶通濾波器的要求增高。

為解決上述面臨的問題，本文提出一種軟件無線電多帶通信號接收方法，實現了軟件無線電對多帶通信號無混疊接收的要求。具體的，用具有可調時間延遲的二階帶通采樣來實現多路混疊信號的接收。該方法同時接收不同頻帶上的多個射頻帶通信號，對多頻段帶通信號進行先采樣、后分離處理，允許采樣后在同一頻段內有多個帶通信號的頻譜發生重疊。

1 二階采樣理論及相位調整濾波器設計

1.1 二階帶通采樣理論

一階帶通采樣理論，假設待采樣的射頻帶通信號為R（f），其帶寬為B。采用采樣頻率fs為兩倍的帶寬，即fs=2B。所有在（n-1/2）fs<|f|<（n+1/2）fs頻率區域內的信號，都定義為索引為n 的信號。經過帶通采樣，所有索引為n 的信號會映射到頻率范圍|f|

基于一階采樣的分析，可得到的中心頻率公式為fc=（2n+1/2）B，帶通采樣后得到的采樣信號為

帶通采樣描述的設計原理，使得原來的頻譜數值在經過帶通采樣分析后，使其在頻域范圍內對折與復制。

若按照理想化的設計理念，即不出現信號的混疊現象，即兩倍帶寬值遠小于采用頻率，且信號為整數時，能夠保證數值滿足fc=（2n+1/2）B。這種限制使研究者提出了二階采用的理念，借助于時間域上所產生的延時現象即頻域上產生的相位差來進行帶通采樣。

二階采樣結構如圖1 所示。

圖1 二階采樣結構

帶通信號經過二階采樣的采樣信號值：

k 的值表示兩種采樣之間的產生的時間延遲，rAδ2（t）作為A 通道的采樣信號，rBδ2（t）作為B 通道的采樣信號。

其頻譜為：

其中γ=e-j2πk2B。

帶通信號R（f）的頻譜用正數部分和負數部分進行表示：

帶通采樣描述的設計原理，使得原來的頻譜數值在經過帶通采樣分析后，使其在頻域范圍內對折與復制，如圖2，3 所示。

圖2 通道A 中的正負頻譜復制示意圖

圖3 通道B 中的正負頻譜復制示意圖

1.2 抗混疊濾波器設計

以兩路帶通信號為例，二階帶通采樣兩通道的頻譜圖分別如圖4、5 所示，從圖中可以看出，通道A 中兩個信號頻譜沒有相角差異，而通道B 中由于ADC B 引入采樣延遲的原理，兩個信號R1（f）和R2（f）的頻譜都分別產生了相角差γn1和γn2。利用兩通道不同的相角差設計抗混疊濾波器FB1（f）和FB2（f），調整兩信號相位，使得經過FB1（f）的輸出信號疊加后信號R2（f）為零，而另一信號R1（f）不變，實現信號R2（f）的分離；經過FB2（f）的輸出信號疊加后信號R1（f）為零，實現信號R1（f）的分離。

圖4 A 通道采樣頻譜

圖5 B 通道采樣頻譜

將抗混疊濾波器FB（f）應用于通道B。于是，恢復的信號頻譜變為：

對每路通道來說，都存在來自n1和n2頻率位置的信號，因此，公式（7）可以進一步分解為：

同時接收兩路信號R1（f）和R2（f）的接收器包括兩個可調的射頻濾波器用來選擇兩帶通信號，經過疊加后輸入到采樣器，兩路信號R1（f）和R2（f）被同時采樣，兩個可重新配置的濾波器FB1（f）、FB2（f）用來消除信號混疊，并并列的輸出R1（f）和R2（f）。

其中，濾波器FB1（f）設計用于恢復R1（f）而消除R2（f）。因此，濾波器FB1（f）應該滿足：

因此，通過解式（9）和（10）可以得到FB1（f）如下式：

為了接收信號R2（f）而消除R1（f），需要設計另一濾波器FB2（f）。利用式（9），（10）所示的同樣的方法可以得到FB2（f），如式（12）所示：

根據上述理論分析后，如下圖所示，多路信號，只要保證混疊個數不超過兩個，則可通過同樣的方法設計相位調整濾波器，實現混疊信號分離。

圖6 BPS 后的頻譜

2 混疊分析與約束條件

2.1 混疊分析

假設一個RF 信號的中心頻率為fc，以采樣頻率fs進行帶通采樣，則可以將第一個奈奎斯特區的中心頻率（稱為鏡像頻率）定義為

這里[·]表示舍入。

假設兩個個帶通信號同時以fAF1，fAF2和鏡像頻率進行接收。圖7 顯示了鏡像頻率和采樣頻率fs之間的關系。

考慮信號fAF2，有不同的fs選擇，它具有三種混疊方式：

通過零頻率附近的自鏡像頻譜進行混疊，如圖7 的區域A所示。

通過周圍的自我圖像頻率進行fs/2 頻率混疊，如圖7 的區域B 所示。

通過另一個信號進行混疊，如圖7 的區域C 所示。

圖7 信號混疊示意圖

傳統的選擇fs方式是為了避免各種混疊，這會限制fs，并且通常需要進行大量計算。在小節1 中，可以通過軟件解決兩個信號重疊引起的鏡像頻譜混疊。因此，在選擇fs上，允許的限制條件會較少。

2.2 約束條件

根據上述規則，給出了采樣率約束條件，以允許采樣后在同一位置出現兩個混疊信號。可以通過以下公式進行詳細的表示[7]：

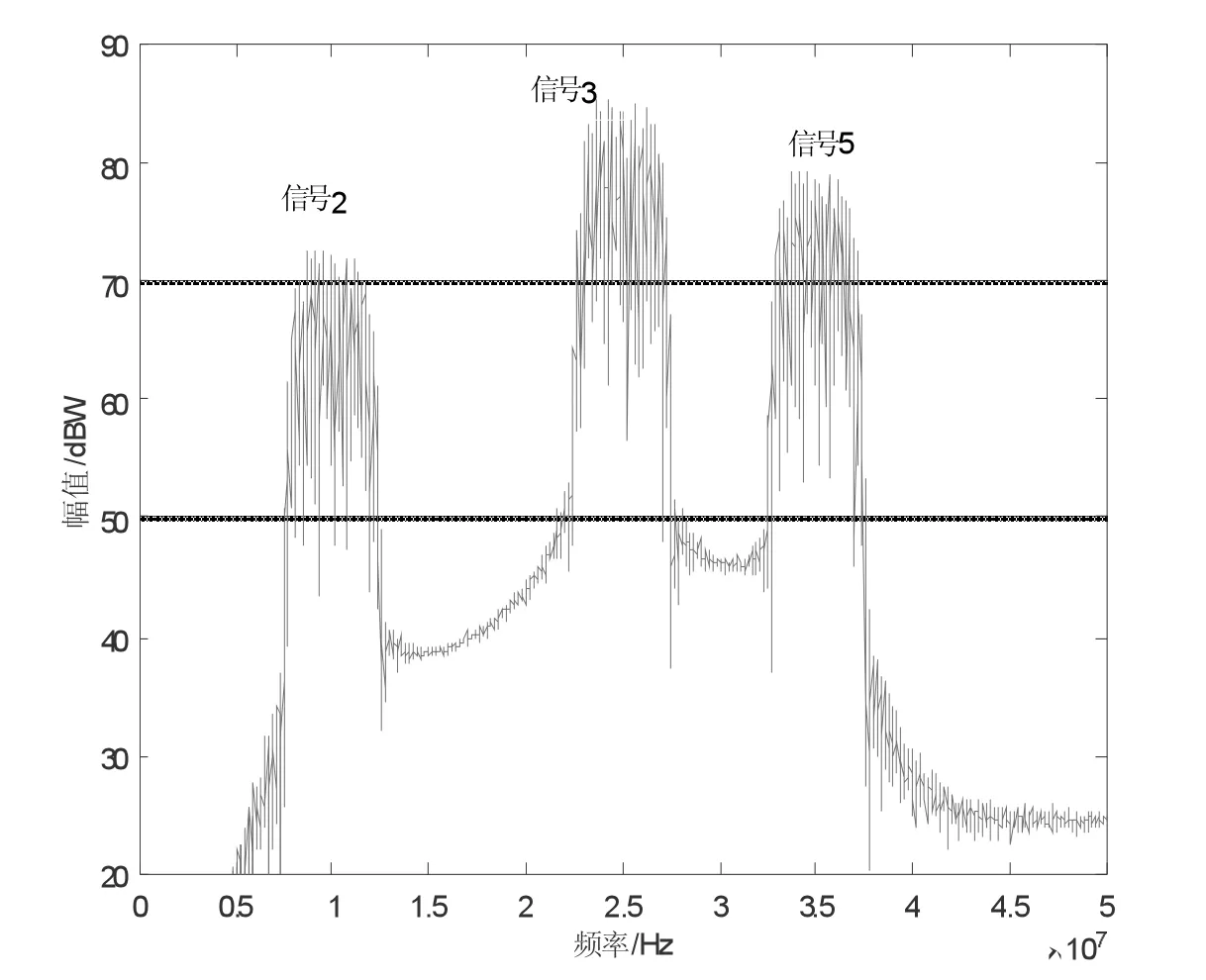
2）如果fDFi

如果fDFi>fs/2-（Bi/2+BG），然后fDFj

這里i=2，3…N，j=2，3…i-1。

3）a）如果fAFli>fAFlj，然后fAFhkfAFhi；

b）如果fAFlifAFhi，然后fAFhkfAFhj；

c）如果fAFlifAFhi。

這里i=2，3…N，j=1，2，3…i-1，k∈[1，N]，k≠i，k≠j。

在上述約束條件下，Bmax代表N 個帶通信號的最大帶寬；BG代表保護帶寬；Bi，fDFi，fAFli和fAFhi分別代表BPS 之后的第一個奈奎斯特區域中信號i 的帶寬，中心頻率，最小頻率和最大頻率。

約束1）表示為采樣頻率要比信號加上保護帶寬的最大帶寬大兩倍。

約束2）表示為僅僅一個信號發生鏡像混疊或者fs/2 邊界混疊。

約束3）表示為僅發生兩個信號在同一位置混疊。

3 多頻段接收機的仿真結果

以5 個輸入信號為例，參數如表1 所示。采樣頻率為100 MHz。兩個采樣通道之間的時間延遲為4×10-10s。

表1 五個輸入信號的參數

帶通采樣（BPS）之后，采樣信號1 和信號2 在10MHz 處進行重疊，信號4 和信號5 在35 MHz 處進行重疊，如圖8 所示。

圖8 BPS 后的信號頻譜

應用小節1 中設計的抗混疊濾波器后，可以分離出重疊的信號。

在圖9 中，信號2 和信號5 被抑制了，而信號1、信號3 和信號4 被保留了。

圖9 抗混疊濾波器FB1 之后的信號頻譜

在圖10 中，信號1 和信號4 被抑制了，而信號2、信號3 和信號5 被保留了。抑制效果超過30dB。

圖10 抗混疊濾波器FB2 之后的信號頻譜

設計并使用進一步的低通或高通濾波器，可以分離五個信號。

4 結論

基于帶通采樣定理，給出了延時可調的二階帶通采樣的結構。通過設計抗混疊濾波器，可以分離出多個個重疊的信號。仿真結果表明，設計的抗混疊濾波器可以有效消除信號引起的混疊現象，解決的帶通采樣中多路信號混疊問題。