基于混合GRASP 算法的輸電網規劃及方案綜合評價研究

翟及第 劉恩彤 李抒軒 石 強 張瀟予

（1、東北電力大學 電氣工程學院，吉林 吉林132012 2、哈爾濱商業大學 計算機與信息工程學院，黑龍江 哈爾濱150000 3、中央財經大學 金融學院，北京100081）

近年來社會經濟發展迅速，電力系統為我國社會經濟發展提供了重要的能源支持，電力是社會發展的重要因素之一，影響著我們生活的方方面面[1]。長期以來，我國重發電、輕輸電以及電網建設投資不足等因素造成了我國電網是電力系統發展中最薄弱的環節。因此，對輸電網規劃問題進行深入研究具有重大的理論意義和現實意義。規劃部門首先應該對各個重要因素進行考慮，然后制定出幾個可行方案，最后再經過充分的系統分析及比較后選定最終方案。

1 輸電網規劃問題描述

在己知條件下，根據當前的待選線路情況，確定出最優的輸電方案。規劃問題表達為下列數學模型：

目標函數：

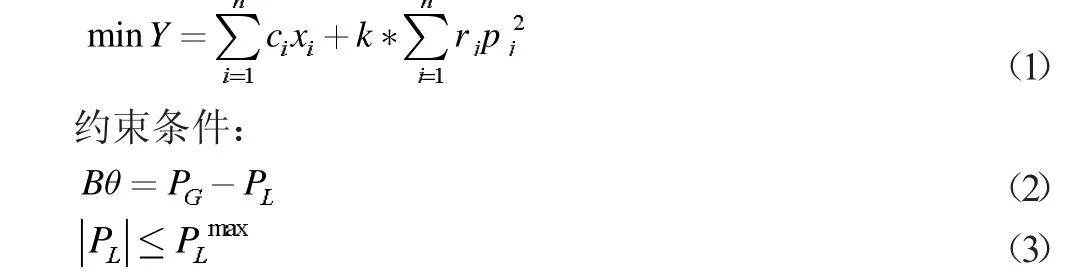
式中，Y 為年綜合費用，其中第一項式子表示網絡投資費用，第二項式子表示網絡的功率損耗費用；xi為被選線路i 的長度；ci表示單位長度線路所需要的花費，單位是萬元/千米；k 為年功率損耗費用系數；n 為加入新線路后網絡線路總數；pj表示支路j 輸送的有功功率大小；rj為支路j 的電阻；θ 為節點電壓相角向量；B 為系統節點導納矩陣；PG為發電機出力向量；PL為負荷向量；PLmax為正常運行時線路最大輸送容量。

2 輸電網規劃模型的混合GRASP 算法

輸電網仿真實現電網暫態、中長期過程的一體化仿真，可以將設備功能、設備電壓以及設備電流等一次性發送給其他仿真設備中，同時，還能接收其他仿真應用所發送的操作事件，并對仿真結果進行處理和監測[2]。

結合GRASP 算法與SA 算法的優點，本文采用混合GRASP算法：GRASP 算法的局部搜索過程引入SA 算法的Metropolis 抽樣策略，使混合GRASP 算法在局部搜索階段可以按概率接受劣解，從而提高算法跳出局部極值的能力[3-5]。混合GRASP 算法的流程圖見圖1。

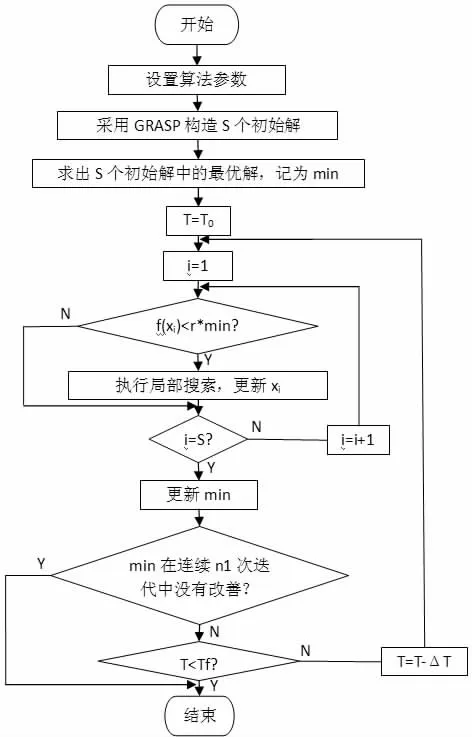
圖1 混合GRASP 算法流程

3 算例分析

該算例采用被廣泛研究的18 節點系統進行試驗。該系統的網絡結構圖如圖2 所示。應用MATLAB 軟件需要設定如下參數：構造階段產生可行解數量S=18；初始溫度T0=700；終止溫度Tf=10；溫度下降步長ΔT=10；構造RCL 的百分比β=0.38；線路篩選系數r=0.5；每千米成本為25 萬元。忽略線路電阻，因而不計網損費用。結果如圖3 所示，該方案與文獻[3]中的最優方案相同。

圖2 18 節點網絡結構

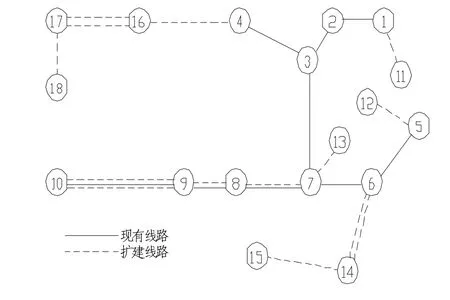
圖3 算例規劃結果圖

表1 混合GRASP、GRASP 和AFSA 的計算性能比較

影響混合GRASP 算法性能的參數主要有構造可行解數量S、溫度Tk、構造RCL 百分比β 等。發電機組爬坡能力，經常會對系統的調峰能力產生一定的限制影響[6]。18 節點系統為例，將這三種參數分別取為不同的數值進行仿真試驗，研究它們對算法求解速度和收斂性能的影響。

（1）構造可行解數量S

將可行解數量S 取為不同的數值，研究其對算法計算時間和收斂性的影響，構造可行解數量越多，搜索就越充分，越容易收斂到全局最優。但構造解數量增加，運算時間增加，效率就會降低。因而，構造解的數量并非越多越好，應該視具體問題而定。對于18 節點系統而言，可行解數量在15 個以上，就能夠獲得最優方案。

（2）溫度Tk

Metropolis 準則是混合GRASP 算法實現全局搜索的關鍵

技術，能使算法順利跳出局部極值，并最終趨于全局最優。而溫度Tk的大小是Metropolis 準則的核心：Tk很大時，算法在廣域內進行搜索，當搜索到新解時對其不做任何判斷而直接接受，即使這個并不比當前解更優；當Tk很小時，此時算法僅僅在一定范圍內的局域里進行搜索，當搜索到新解時，首先將其與當前解進行比較，只有優于當前解才被接受。因此，算法的收斂性對Tk的選取要求很高。

（3）構造RCL 百分比β

輸電網規劃中，當β=1 時,每次取最優的線路完成加線操作，形成一個完全的貪婪過程；當β=0 時，每次的加線操作可以選擇任何一條待選線路加入RCL，而不需對其有效性進行比較和分析，此時構造過程是一個完全的隨機過程。一般情況下，β 取值為0.3～0.55 比較合理。

4 結論

根據GRASP 算法和SA 算法的特點，將其組合形成混合GRASP 算法。該混合算法結合了以上兩種算法的優點，計算效率提高，收斂性能大大增強。根據輸電網規劃問題的特點，引入篩選機制，進一步提高了算法的計算速度。將該算法應用于求解輸電網規劃問題，仿真實例證明，具有很高的可行性與優越性。