信號對單模激光損失模型輸出特性的影響

葉 慶,李景艷,卿秀華,肖丹琪

(1.武漢紡織大學電子與電氣工程學院,湖北 武漢 430074;2.浙江工業大學理學院,浙江 杭州 310023)

1 引 言

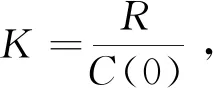
本文考慮了量子噪聲實部和虛部之間的關聯,運用單模激光損失模型的場幅新方程,用線性化近似方法[6],計算了反映激光動力學性質的光強關聯函數[7-8]和平均光強相對漲落C(0)以及信噪比R[9-11],分析了輸入信號等系統參數對定義量K的影響,得到了一些新的結果。

2 單模激光方程的計算方法及結果

2.1 線性化近似及關聯函數、平均光強相對漲落、信噪比

輸入周期信號后的單模激光損失模型的光強方程為:

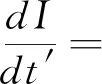
(1)

噪聲滿足如下統計性質:

(2)

式(1)、(2)中,a0,A為凈增益系數和自飽和系數；I,B,Ω分別為光強、輸入信號振幅和頻率；pR(t′)為泵噪聲實部；εr(t′)為相位鎖定后的量子噪聲；P,Q是泵噪聲和量子噪聲強度；τ是泵噪聲自關聯時間；λq為量子噪聲實虛部之間的關聯系數,其取值范圍為-1≤λq≤1。

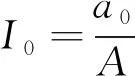
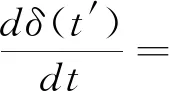
(3)

其中,γ=2a0。

3.2 體位的正確擺放，俯臥位，胸腹部懸空而不直接接觸臺面，避免對大血管的壓迫以減少出血，使胸腹腔容積不減少，使全麻下肺部擴張不受限。

根據穩態平均光強關聯函數的定義:

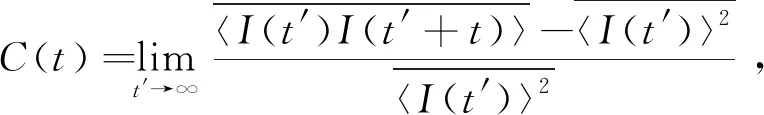
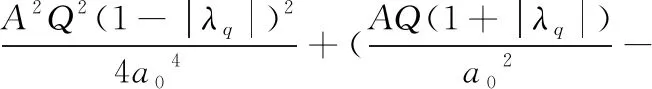
(4)

其中,令t=0,得到穩態平均光強相對漲落:

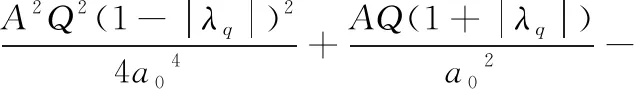
(5)

對式(4)進行傅里葉變換,得輸出光強功率譜為:

S(ω)=S1(ω)+S2(ω)

(6)

其中,S1(ω)為輸出信號功率譜；S2(ω)為輸出噪聲功率譜,具體表達式為:

(7)

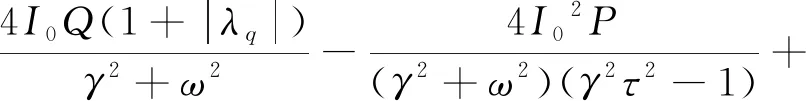
(8)

輸出信號總功率[12]為:

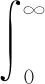
(9)

信噪比定義為輸出信號總功率與ω=Ω處的單位噪聲譜的平均功率之比(僅取ω>0的譜):

(10)

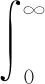
(11)

2.2 單模激光系統的輸出信號與穩定性的優化選擇

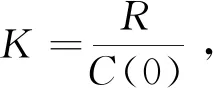
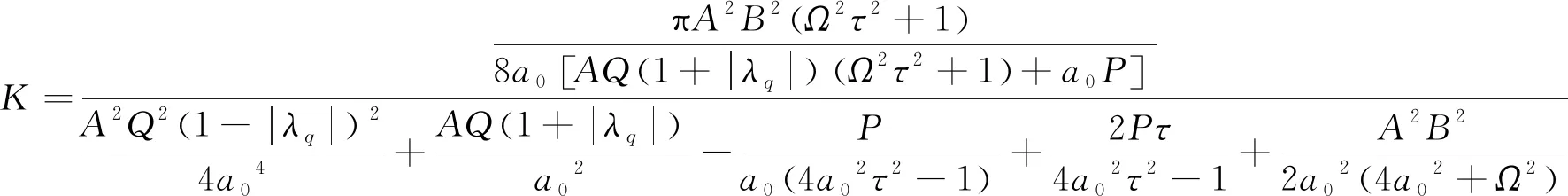
(12)

該量描述了激光系統的優化輸出特性,當K取極大值時,系統達到最佳輸出信號質量與穩定性的配置。

3 系統穩定性K隨凈增益系數a0的變化關系

圖1(a),圖1(b)繪出了信噪比R與系統漲落C(0)之比K隨凈增益系數a0的變化曲線,發現:在所給定的參數下,K有兩個極大值,雙峰,即出現雙次優化,第一個峰值尖銳,第二個峰值平坦,而且曲線在第一個峰之后隨著a0增大迅速單調遞減,出現極小值后遞增,繼而出現第二個極大值后單調遞減。由式(12)可知,其中參數的改變對峰值的大小和位置均有影響。

圖1(a)是以輸入信號振幅B為參數繪出的K-a0曲線,可以看到,曲線出現兩個峰值,第一個峰值高于第二個峰值,當輸入信號振幅B增大時,曲線峰值增大,隨著B等值增大時,峰值等值增大。同時,兩個峰值的半高寬幾乎沒有變化,峰值位置也基本不變。圖1(b)是以信號頻率Ω為參數繪出的K-a0曲線,從圖中看出,第一個峰值略小于第二個峰值,隨著Ω的減小,曲線峰值降低,同時,隨著Ω等值減小,峰值也等值減小；兩峰值半高寬幾乎沒有變化,峰值位置也幾乎不變。圖2(a)中,當Ω持續減小,即12.00≤Ω≤12.50時,曲線第一個峰值降低很快,第二個峰值等值減小,直至Ω=10.00時,曲線幾乎呈現單峰現象,如圖2(b)所示。

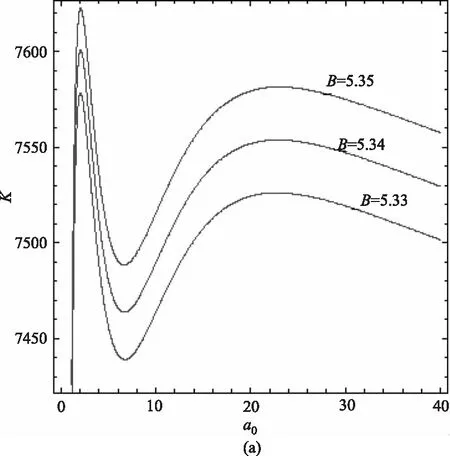
圖1 B、Ω為參數時K隨a0變化的函數關系圖(A=1,P=0.1,Q=0.005,τ=0.2,λq=0.5)

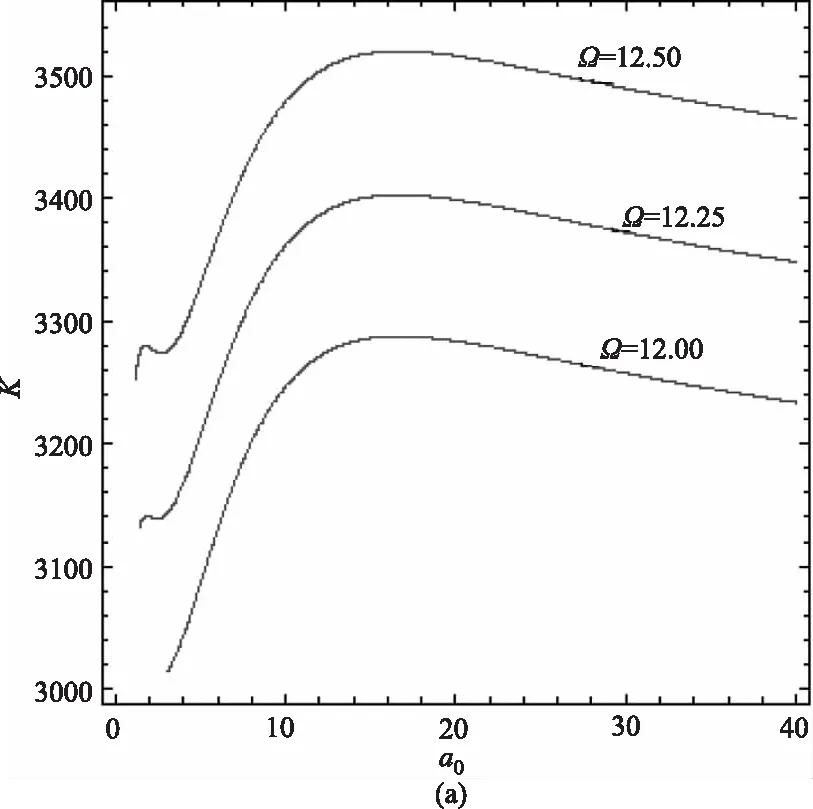
圖2 Ω為參數時K隨a0變化的函數關系圖(A=1,P=0.1,Q=0.005,τ=0.2,λq=0.5)

4 系統穩定性K隨自飽和系數A的變化關系

圖3(a),圖3(b)繪出了信噪比R與系統漲落C(0)之比K隨自飽和系數A的變化曲線,發現:在所給定的參數下,K只有一個極大值,單峰,而且曲線在單峰之后隨著A增大單調遞減,在參數B的圖形中,曲線隨A的增加會趨于相同的K值,但在參數為Ω的圖形中,曲線隨A的增大K卻有不同的大小。

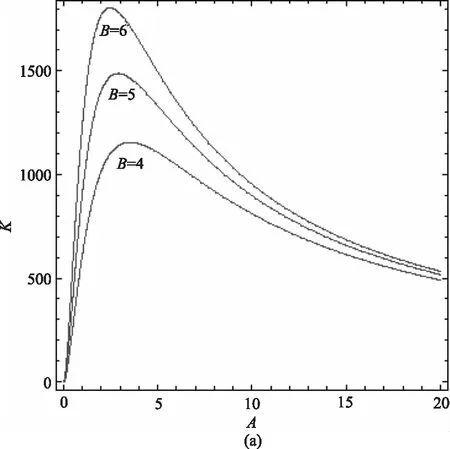
圖3 B、Ω為參數時K隨A變化的函數關系圖(a0=2,P=0.1,Q=0.05,τ=0.1,λq=0.1)

圖3(a)是以輸入信號振幅B為參數繪出的K-A曲線,可以看到,當輸入信號振幅B增大時,曲線峰值增大,隨著B等值增大時,峰值近似等值增大。同時,峰的半高寬度略有減小,峰值位置略有左移。圖3(b)是以輸入信號頻率Ω為參數繪出的K-A曲線,從圖中看出,隨著Ω的增大,曲線峰值升高,隨著信號頻率等值增大時,峰值也是等值增大,峰值的半高寬幾乎不變,峰值位置略右移。

5 系統穩定性K隨泵噪聲自關聯時間τ的變化關系

以B為參數,信噪比R與系統漲落C(0)之比K隨泵噪聲自關聯時間τ的變化曲線如圖4(a),4(b)所示,發現:在所給定的參數下,曲線隨泵噪聲自關聯時間的增大呈單調遞增的趨勢,當 2≤B≤5,K值遞增較快,當5≤B≤8時,K值遞增緩慢,明顯可以看出隨著B等值增大時,K值增大速度越來越緩。正如圖4(b)所示,當8≤B≤15時,很明顯可以看出,當K值幾乎等值增大時,B值卻不是等值增大的。

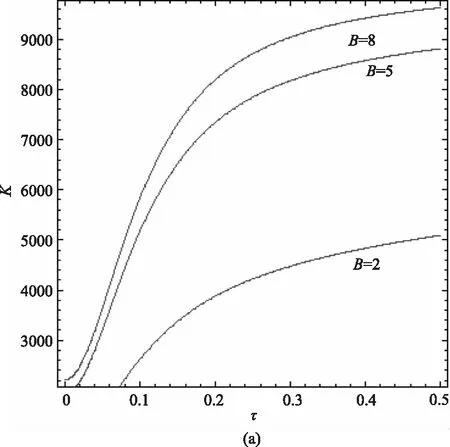
圖4 B為參數時K隨τ變化的函數關系圖(a0=1,A=4,P=0.1,Q=0.005,λq=0.5)

圖5(a)、(b)繪出了以輸入信號頻率Ω為參數繪出的K-τ曲線,從圖中看出,在輸入信號頻率8≤Ω≤10中,當Ω稍大時,曲線呈現的是上凸式單調遞增的趨勢；當頻率較低時,如0.9≤Ω≤1.1時,曲線呈現的是下凹式單調遞增的趨勢；同時Ω增大,曲線K值增大。

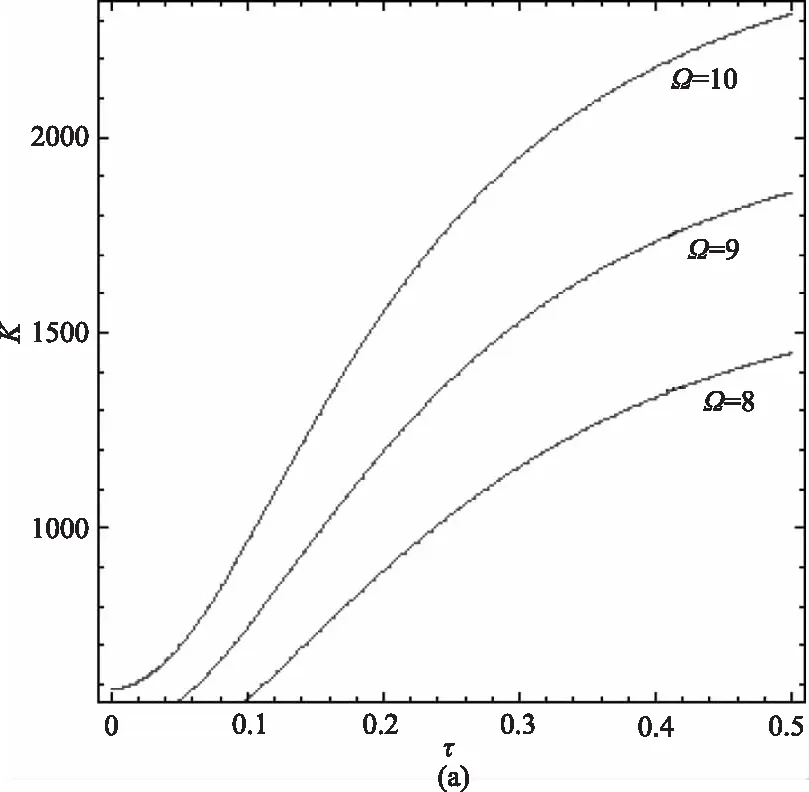
圖5 Ω為參數時K隨τ變化的函數關系圖(a0=1,A=4,P=0.1,Q=0.005,λq=0.5)

6 結 論

綜上所述,K隨激光系統的凈增益系數a0存在未研究發現的雙極大值；與自飽和系數A之間存在單極大值,極大值即是系統最佳匹配狀態,發現,極大值的半高寬越窄,峰值越尖銳,說明優化性能更好；與泵噪聲自關聯時間τ不存在極大值,但是隨參數的變化有不同程度的影響；曲線峰值均會隨輸入信號振幅B、輸入信號頻率Ω的增大而增大；同時,K-τ曲線中K值也是隨著信號振幅B和頻率Ω的增大而增大,也就是說,輸入信號振幅、頻率的增大均能優化激光通訊系統輸出性能。