多物理場下望遠鏡主次鏡失調分析研究

賀 璧,任 戈,扈宏毅,劉儒貞

(1.中國科學院光電技術研究所,四川 成都 610209；2.中國科學院光束控制重點實驗室,四川 成都 610209；3.中國科學院大學,北京 100049)

1 引 言

光電跟蹤設備在天文觀測、航空航天、科學研究等領域有著廣泛的應用。某型光電跟蹤設備采用主、次鏡構成的卡式望遠鏡系統,對目標光縮束,然后進行成像探測。主、次鏡通過各自的支撐組件安裝在鏡筒上,由于鏡筒在日照、振動等情況下,主次鏡間相對位置的變化產生失調,會對目標探測帶來像差,影響光電設備的探測精度。目前,光電跟蹤設備應用場景從固定平臺走向運動平臺,工作環境變得越來越嚴酷,這些條件均會對光電跟蹤設備的性能造成影響。為評估各種環境與振動對光學系統光路失調的影響,國內外都對此進行了大量的研究。Lee Jun Ho針對某型航空相機,利用有限元分析軟件與Zemax軟件,采用Zernike多項式擬合相機鏡面變型后的面型,分析溫度的梯度變化與重力的共同作用對成像質量的影響[1]；Zhang Heng針對某空間光學平臺進行了微振動的動力學仿真與試驗分析,模擬了光學平臺上的主、次鏡的鏡面變形情況[2]；Steven Griffin與John Blackburn建立針對光電吊艙建立了相關的有限元模型與視軸抖動模型,使用測得的實際載體的振動功率譜來對模型進行功率譜相應分析,并將結果與實際測得結果進行對比,結果顯示多數情況下實際的視軸抖動數據比預測值低[3]；Brandon J.Dilworth針對地面與月軌衛星的激光通信系統,從系統的裝配工作開始進行動力學試驗,在有限元軟件中迭代建立了該系統的動力學模型,并搭建了視軸抖動測試平臺,驗證了基于有限元模型的視軸抖動模型的預測的有效性[4]；Keith B.Doyle則針對火星軌道的終端設備與地球終端間的激光通信系統,進行了視軸抖動分析,并提出了一種六自由度柔性隔振結構減小視軸抖動[5]；Cho Myung等人則利用采集到的完整的三天的環境數據,針對TMT望遠鏡,仿真了其在該情況下望遠鏡機架上溫度隨時間變化的分布[6]；Zhong Jie針對上海的65 m射電望遠鏡的主鏡與次鏡在光照與溫度場的作用下進行了熱仿真分析,得出次鏡上的最高溫度可達144.9 ℃[7]。在振動和太陽直射和高溫條件下進行工作時,因光學元件與相關支撐結構的位置與角度變化,光電跟蹤系統產生的光路失調的影響,是設計人員不得不考慮的問題。

以上的國內外研究中,針對光電設備的有關研究,均為立足于對光電設備的性能分析,針對光電設備的仿真與試驗均比較復雜,且部分研究并未考慮載荷加載的簡易性和代表性。本文的研究對象為某型光電跟蹤設備,其光學系統為離軸主次鏡結構,見圖1,其中反射鏡1為主鏡,反射鏡2為次鏡。該光電跟蹤設備工作時需承受振動和太陽輻射,見圖2。針對該型光電跟蹤設備,本文利用相關標準,針對振動和熱載荷與加載方式進行了相關的簡化,對鏡筒結構變形造成的光學元件的偏轉與位移進行分析計算,供光學設計人員評估鏡筒變形帶來的像差并進行校正,對鏡筒主要結構提出修改意見,并對修改后的設計進行了相關的仿真與對比。

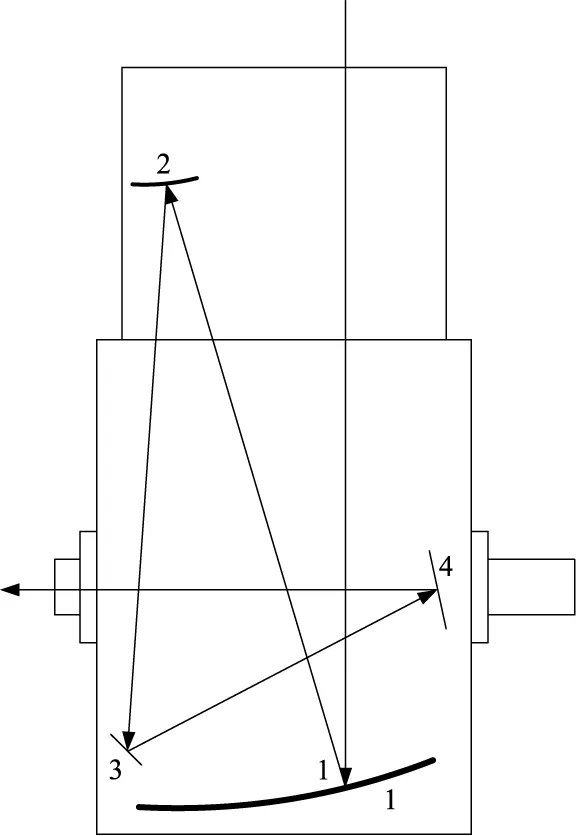
圖1 離軸光學系統

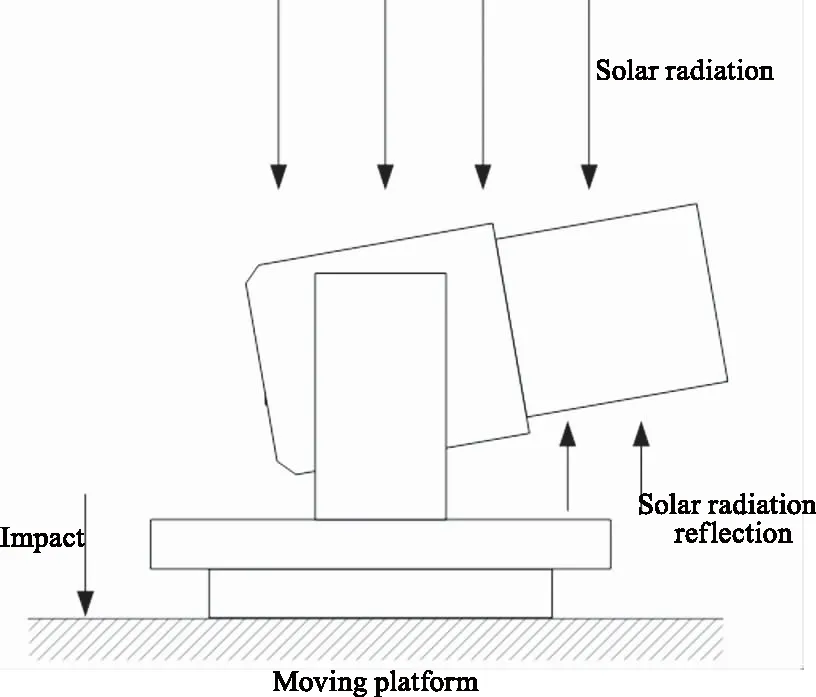
圖2 動平臺上的光電跟蹤設備的太陽輻射與振動載荷

2 動力學和熱力學分析基礎理論

2.1 動力學理論

根據經典力學理論可知,物體的動力學通用方程為[8]:

(1)

式中,M為質量矩陣；C為阻尼矩陣；K為剛度矩陣；x為位移矢量；F(τ)是動載荷矢量。在線性結構分析中,與時間τ相關的量都將被忽略,于是上式可簡化為:

Kx=F

(2)

穩態熱力學分析的一般方程為:

Kt=P

(3)

式中,K為傳導矩陣,包括導熱系數、對流系數、輻射系數和形狀系數；t是節點溫度向量；P是節點熱流向量,包含熱生成。

對本文分析的系統,將太陽熱輻射等效為熱流,且不考慮鏡筒與外界環境發生熱輻射,因此本文進行熱力學分析中主要涉及的是熱傳導和熱對流。系統處于熱穩態時,溫度不隨時間變化,求解的基本方程為:

[K1]e{t}e={P}e

(4)

2.2 熱彈性力學問題

隨著溫度的升高,鏡筒發生膨脹變形,由于結構的約束、溫度分布的不均以及零部件材料的不同,結構會產生內應變εt與應力σt。根據線性膨脹原理,溫度升高Δt,則引起伸長:

Δl=αlΔt

(5)

根據廣義胡克定律,應變與應力分別為:

(6)

σt=Eεt=EαΔt

(7)

式中,E為楊氏模量；α為線膨脹系數。

3 振動和熱輻射

假設光電跟蹤設備由卡車在高速公路上運載,地面運動車輛的振動環境是帶有峰值和谷值的寬帶隨機振動,其振動響應分析為一個復雜的動態過程。為了簡化計算,方便得到具有參考意義的反映主次鏡位置變動的參數,在進行分析時,將垂直軸方向上的振動等效為1.04 g的垂直向下的加速度載荷,將動力學問題轉化為靜力學問題。

由于白天鏡筒結構的主要溫度載荷是太陽輻射[9],選用條件為:太陽輻射總強度1120 W/m2,最高溫度44 ℃,風速為0.25 ～1.5 m/s,該條件代表了較不嚴酷條件,其所在地區為具有高溫和中等偏低的濕度并伴隨高強度太陽輻射,包含了中國大部分地區。鏡筒表面涂有TiO2白漆,其熱輻射吸收率為15 %,反射率為85 %[10]。選擇1986—1990年間重慶地區為代表,夏季地表對太陽輻射的平均反射率17 %[11]。

1) 進行靜力學分析時,加載1.04倍的標準重力加速度,對鏡筒進行水平狀態和上仰45°與上仰90°三個姿態的靜力學分析,支撐約束加載見圖3。

圖3 支撐約束加載

2) 進行熱穩態分析時,此時不考慮重力影響,由于太陽直射鏡筒時,鏡筒變形最大,因此,此時僅考慮太陽直射的情況。鏡筒上表面加載太陽輻射強度Q1=1120×15 %=168 W/m2,鏡筒下表面加載地面反射為Q2=1120×17 %×15 %=28.56 W/m2,取29 W/m2,設定環境溫度為44 ℃,空氣自然對流,熱對流系數取為5 W/(m2·K),熱載荷加載見圖4。

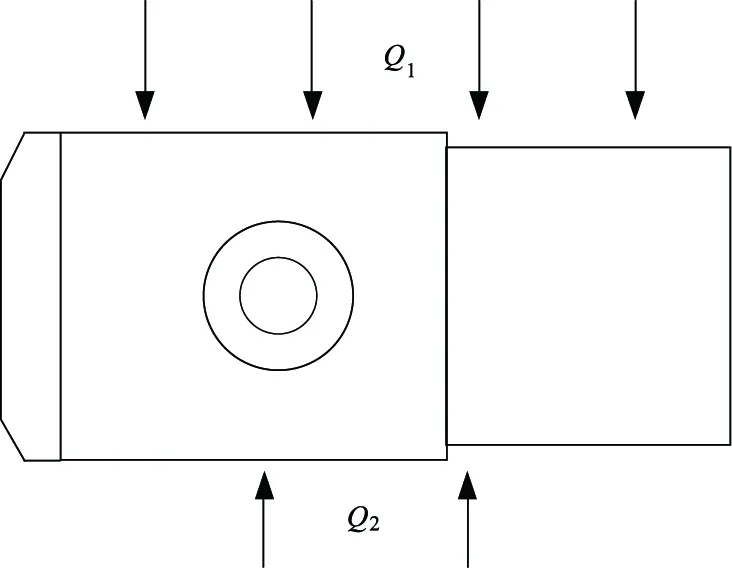
圖4 太陽輻射載荷分布

3) 進行多物理場耦合分析,對鏡筒在1.04 g的等效重力場和溫度場中進行分析。

4 仿真分析

為了方便進行三維建模以及順利進行有限元分析,在Pro/E中對主鏡筒建模,忽略了一些對仿真結果影響小的結構與零件,對一些不影響結果分析的復雜結構進行了簡化等效處理,再將所建好的三維模型導入到Ansys Workbench進行有限元分析。本仿真針對某型光電跟蹤設備鏡筒進行了兩次仿真,第二次為對修改后的鏡筒的仿真分析。對鏡筒進行了靜力學分析,熱穩態分析以及考慮熱輻射與重力作用的多物理場耦合分析。

4.1 估算分析方法

為在Ansys Workbench中較為方便地估算出鏡面偏轉θ,需選取鏡面參考面,估算原理圖見圖5,主、次鏡上的參考面見圖6。鏡筒變形前,反射鏡參考面在平面XOY上,如圖5中虛橢圓所示；鏡筒變形后,反射鏡參考面如圖5中實橢圓所示。

(a)

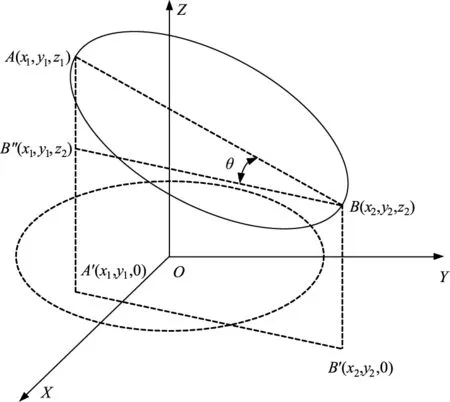
圖5 估算原理圖

假設參考面為理想不發生扭曲變形的面,則A點為參考面上Z軸方向上最大位移點,B點為參考面上Z軸方向上最小位移點,此時A點與B點在參考圓面的同一直徑上,則有:

(8)

由于θ本身為微小量,所以有:

θ≈sinθ

(9)

由于反射鏡自身也會出現微小形變,最大位移點A與最小位移點B很難嚴格處于同一直徑上,若A點、B點很明顯不處于同一直徑上,則分別取其對應的在同一直徑上的點分別進行計算,取其最大值作為反射鏡偏轉角θ。

4.2 仿真計算結果

左右軸頭、主鏡筒蓋、次鏡與調焦機構間連接零件、調焦機構設為結構鋼,其余零件均設置為鋁合金材料。為了對一些關鍵部件分析準確,對鏡筒中主要的受力支撐結構以及會對仿真結果產生影響的孔結構進行局部細化,使該處單元的基本尺寸為該結構最小尺寸的一半。劃分網格后,鏡筒的有限元模型見圖7,一共536376個單元,908914個節點。

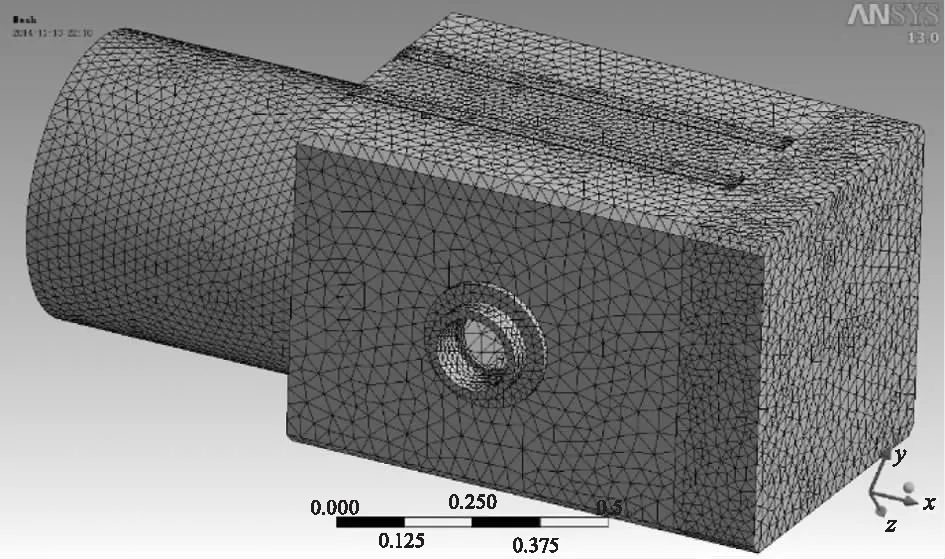
圖7 主鏡筒有限元模型

通過仿真,太陽直射鏡筒條件下,鏡筒溫度達到熱穩態時,鏡筒上的最高溫達55.643 ℃,最低溫為48.707 ℃。鏡筒的溫度分布云圖見圖8。

圖8 主鏡筒的溫度分布

對鏡筒處于0°,45°以及90°的仰角情況下,進行了1.04 g的等效重力場中的靜力學分析；在太陽垂直照射鏡筒上表面條件下,對鏡筒進行了的熱穩態仿真；在鏡筒水平地處于等效重力場中且太陽垂直照射鏡筒情況下,對鏡筒進行溫度場與等效重力場耦合作用的多物理場仿真。算得主鏡與次鏡的偏轉位移見表1。

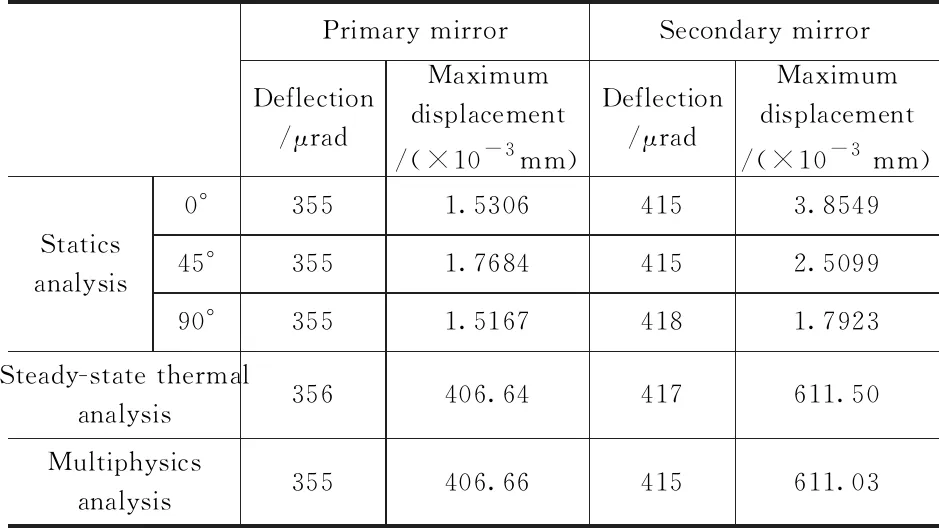
表1 主鏡與次鏡偏轉與位移

有限元分析結果顯示主鏡與次鏡的偏轉量較大,且重力影響與熱載荷對偏轉量影響均很大,因此需要減小鏡筒兩端的力矩并提高鏡筒整體剛度,減小熱載荷對鏡筒的主鏡、次鏡偏轉的影響。因此,將次鏡筒縮短40 mm,并將次鏡的支撐由次鏡筒支撐改為由單獨的支撐架支撐；將次鏡與調焦機構的連接件進行加固設計；主鏡蓋設計得更為緊湊,并將主鏡蓋的材料換為鑄鐵,且在主鏡蓋上設計一個500 mm×386 mm的減重方孔,主鏡蓋減重約18 kg。鏡筒原次鏡支撐結構見圖9(a),新次鏡支撐結構見圖9(b)。

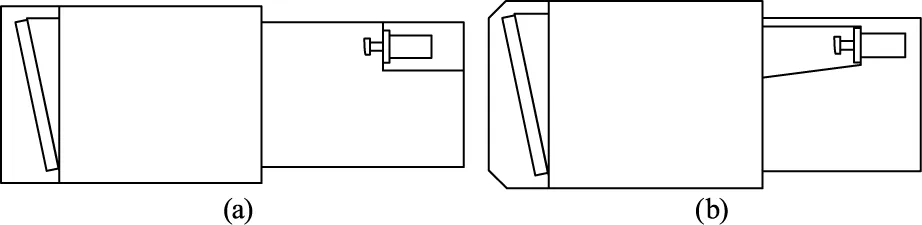
圖9 主鏡筒結構

對鏡筒新結構進行新一輪仿真分析,劃分網格后總節點數為1015101個,總單元數為551890個。網格化后的有限元模型見圖10。太陽直射鏡筒條件下,鏡筒溫度達到熱穩態時,鏡筒上的最高溫達54.525 ℃,最低溫為49.714 ℃。鏡筒的溫度分布云圖見圖11。在此條件下,算得主鏡與次鏡偏轉位移見表2。

4.3 總 結

由所得到的結果所示,鏡筒新結構變形對反射鏡的偏轉影響相對于原來結構對反射鏡偏轉的影響小得多。從所得的仿真結果來看,熱載荷引起鏡筒形變對反射鏡的偏轉始終影響很大,因此,在鏡筒結構確定后,在光電跟蹤設備實際使用時,溫度熱載荷變化是影響光電跟蹤設備性能的一個重要因素。本文通過仿真模擬一個較為惡劣的環境,估算出鏡筒在此環境下的反射鏡偏轉與位移,為對光電跟蹤設備鏡筒的形變產生的影響進行修正補償提供參考數據。

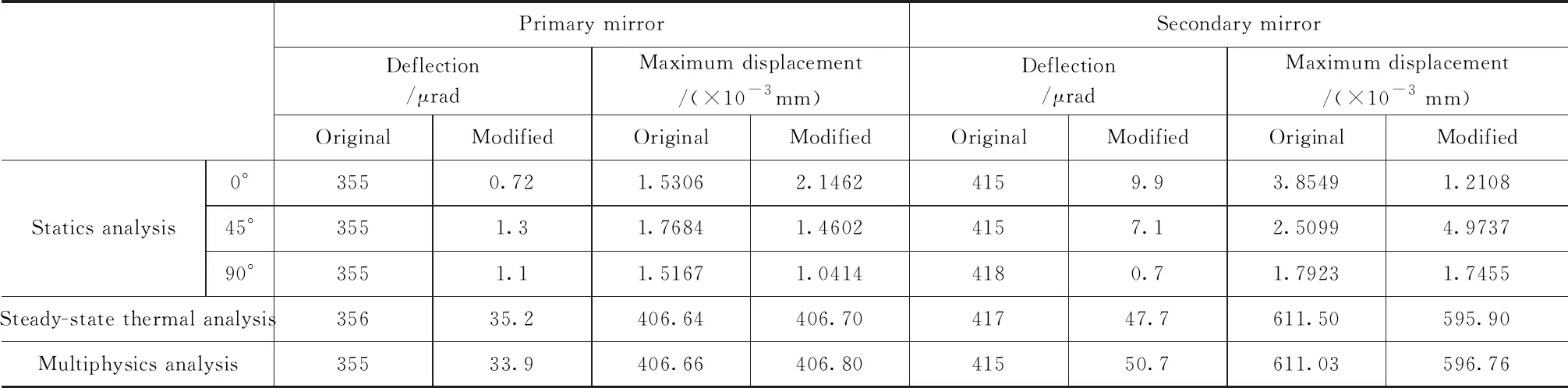
表3 主鏡與次鏡的偏轉與位移在修改前后的結果對比

5 結 論

通過Ansys Workbench對光電跟蹤設備進行有限元分析,可知,熱載荷對鏡筒反射鏡的偏轉位移影響始終較大,因此,需要對鏡筒中一些受變形影響的關鍵部件進行相關的設計,盡量隔離其受到熱載荷的影響,并減小鏡筒兩端相對水平軸的力矩。仿真時,雖然考慮了太陽直射的輻射,地面反射的太陽輻射,以及空氣自然對流,還有重力的影響,但并未考慮地面散射,鏡筒與環境的熱輻射,以及軸頭的熱傳導等因素；而且本文是對振動與熱載荷進行了一定的等效處理,因此,該仿真與真實情況有一定的差別。

通過仿真數據,相關的隔離減重設計較好地實現了相關的功能目的,所得到的數據也可給補償校正提供一定的參考。所用采用的反射鏡偏轉角度估算方法,也可以為進行動態熱載荷條件下的鏡筒反射鏡偏轉補償修正提供一定的參考。