基于雙向循環神經網絡的漢語語音識別*

李 鵬 楊元維 高賢君 杜李慧 周 意 蔣夢月 張凈波

(長江大學地球科學學院 武漢 430100)

0 引言

語音識別是指計算機能夠理解人的語言，將音頻信息轉換成文本信息。隨著互聯網技術和人工智能技術的飛速發展，語音識別被逐漸應用到各個領域內，因此與之相關的研究也越來越受到重視。特別地，Google、Microsoft、科大訊飛、百度等公司，都爭相在語音識別上投入大規模的研發，推出相關的算法、軟件及應用。語音識別的產業化也進一步推動著語音識別技術的發展。

語音識別的相關研究最早可以追溯至20 世紀50 年代AT&T 貝爾研究室。該研究室的Audry 系統基于簡單的孤立詞，能夠對10 個單音節單詞進行識別。在60 年代提出的動態時間規整(Dynamic time warping,DTW)方法[1]，有效解決了兩個不同長度音頻片段的對齊問題。隨后語音識別研究進一步發展，線性預測分析技術(Linear predictive coding,LPC)被擴展應用[2]，DTW也基本成熟。與此同時，隱馬爾科夫模型(Hidden Markov model,HMM)理論被提出。隨著HMM技術不斷成熟和完善，語音識別從原來的模板匹配的方法轉變為概率模型的方法[3]，并且以HMM 相關模型為主要研究方法[4]。而后，人工神經網絡(Artificial neural net,ANN)逐漸被用于語音識別的研究中[5]，以尋求新的突破。楊華民等[6]采用ANN 進行語音識別的原理，給出了求解語音特征參數和典型神經網絡的學習過程，通過具體的實例展示了ANN 技術的實用化。但傳統神經網絡本身也存在需要大量標記數據等問題。2006年，Hinton等[7]提出了深度學習的概念。此后，深度學習以其良好的普適性被應用到語音識別領域里，打破了HMM的主導局面，極大地提升了基于傳統神經網絡的語音識別系統的性能，突破了某些應用情景中的識別瓶頸[8]。

在深度學習的大環境下，最初應用在語音識別里的是深度置信網絡(Deep belief network,DBN)[9]，能夠對神經網絡進行預訓練以達到使模型穩定的效果。而后深度神經網絡(Deep neural network,DNN)、卷積神經網絡(Convolution neural network,CNN)和循環神經網絡(Recurrent neural network,RNN)等相繼問世，這引發了人們對各類神經網絡進行深入研究。張仕良[10]指出基于DNN 的訓練速度相較于CNN 或RNN 的更快，然而利用DNN 進行語音識別卻未能良好解決其中較為重要的時序問題。DNN 和CNN 對輸入的音頻信號的感受視野相對固定，所以對于與時序相關的問題不具有較好的處理能力。RNN 在隱含層存在反饋連接，它能通過遞歸來挖掘序列中上文的相關信息，在一定程度上克服DNN 和CNN 的缺點[11]，但是卻無法挖掘序列中下文的相關信息。隨后，Schuster等[12]提出雙向循環神經網絡(Bidirectional RNN,Bi-RNN)，并彌補了RNN 的缺點，能夠同時利用上下文信息，在時序問題上相對于RNN識別正確率取得了進一步的提升。因此本文基于Bi-RNN 模型在語音識別方面進行研究，從言語產生與言語感知的角度對Bi-RNN 進行更深層次的解讀，探討了Bi-RNN 模型在不同噪聲環境中的識別效果，并進行大量的實驗，選取出一套適合本模型的參數，進一步地降低了語音識別錯誤率。

在進行語音識別之前，本文首先對音頻進行預處理。預處理包括對音頻進行預加重、分幀和加窗。對預處理之后的音頻做語音特征提取，即將音頻轉化為梅爾頻率倒譜系數(Mel frequency cepstral coefficient,MFCC)。再用訓練集迭代訓練模型，將訓練后的模型對測試集進行實驗，最后得到識別結果。

1 循環神經網絡結構

1.1 人工神經網絡

ANN 是一種由大量簡單處理單元(神經元)按照不同的連接方式組成的運算模型。一個神經元的模型如圖1所示。在結構上可以將人工神經網絡劃分為3層——輸入層、隱含層、輸出層(圖2)。神經網絡的輸入/輸出關系表示為下列公式：

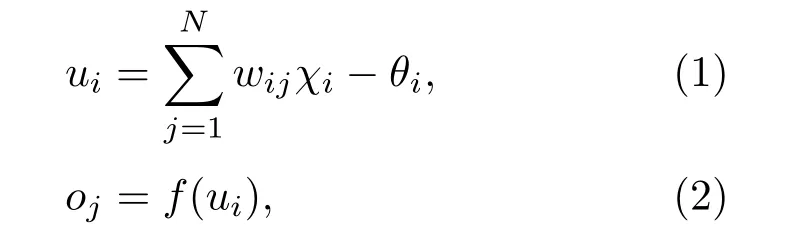
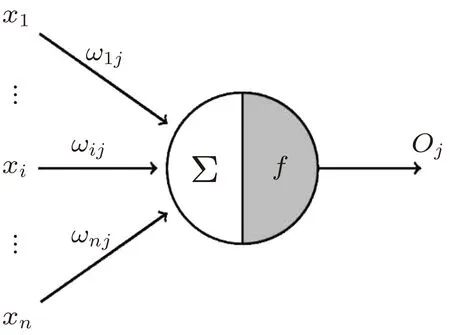
圖1 神經元模型Fig.1 Neuron model

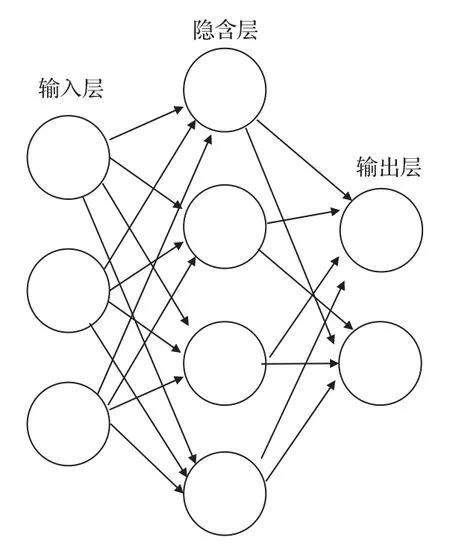
圖2 神經元網絡Fig.2 Neural network

其中：wij為連接權重，即神經元i與神經元j之間的連接強度；χj為神經元i的某個狀態變量；θi為神經元i的閾值；ui為神經元i的活躍值；oj為神經元i的一個輸出；f為激活函數。

1.2 單向循環神經網絡

在DNN 或者CNN 中，它們的基本前提是每層之間的節點連接是相互獨立的。這樣的結構存在一個潛在的弊端，即無法對具有時間特性的相關信息來建立模型。然而語音識別卻是一個典型的具有時間特性的問題[13]，輸入順序是一個非常重要的因素，它不類似于圖像識別——對輸入的順序無特殊要求。因此為了解決DNN、CNN 的這種弊端，對RNN的研究在20世紀80年代迅速開展起來。

相較于DNN或者CNN，RNN最大的不同之處就是在隱含層中增加了節點之間的連接[14-15]，這使得隱含層的輸入不僅來源于輸入層，還包含了隱含層前一時刻的輸出。RNN 是根據人的記憶原理而產生的。比如一句話“我要去飯吃了”，這句話聽起來很奇怪，這是因為大腦接收到這段話會受到刺激，進而產生預測功能。如果“我要去”后面跟著“吃”，就感覺很正常。從言語產生和言語感知的角度來理解，這是因為大腦對每個字的先后順序是有一定的判斷的。其模型如圖3所示。

在RNN 中，上一時間點到當前時間點變換過程中每層的權重W是共享的，這樣在很大程度上減少了訓練參數數目。圖3 中，W0表示輸入層與隱含層之間的權重值，W1表示上一時刻隱含層到當前時刻隱含層之間的權重值，W2表示隱含層與輸出層之間的權重值；S(t)表示隱含層的第t個RNN 節點的輸出狀態。

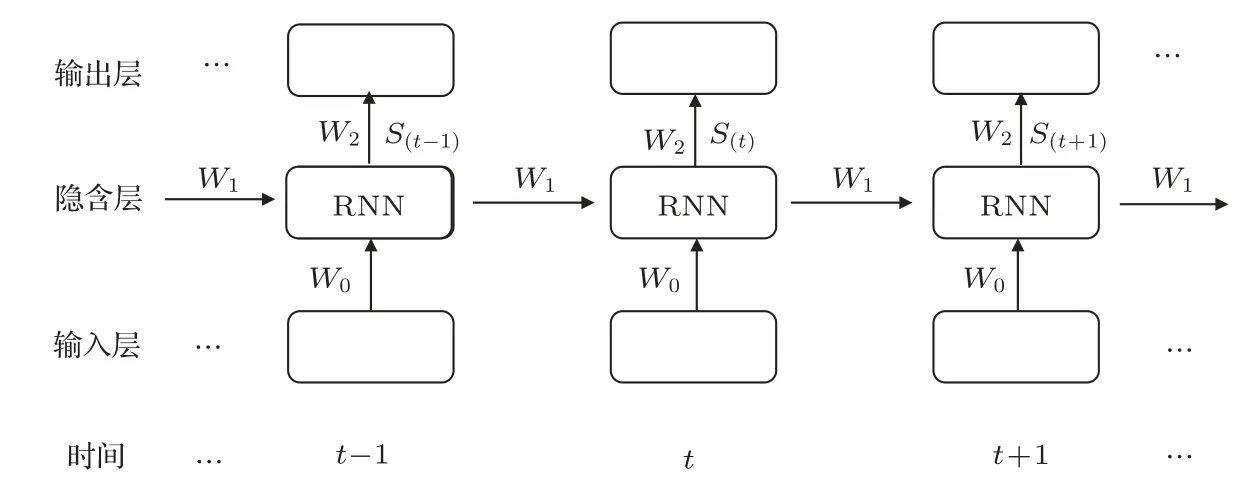
圖3 循環神經網絡結構Fig.3 The structure of RNN

1.3 雙向循環神經網絡

由1.2 節可知，傳統的RNN 只是利用了上一時刻的信息，而在具有時間特性的語言序列中，有很多需要同時聯系過去與未來時刻的信息。同樣是這句話“我要去飯吃了”，如果說出“飯”的前面一個字是什么，大腦可能需要時間思考一下，甚至要再默念一遍這句話，而不是反著讀這句話“了吃飯去要我”，但最終都會找到這個字。這種現象引發了兩個很值得思考的問題：第一，大腦可以通過一定的規則而找到“飯”這個字前面的字，這種現象可以理解為大腦對于信息的存儲，并不是簡單的單獨存儲，而是一種鏈條式的存儲方式，這種方法有個極大的好處，大腦只要記住相關的存儲規則或者方法就可以，這樣大大節省了很多空間。第二，大腦很難進行反方向的搜尋信息。基于這種現象，Bi-RNN 應運而生，相對于CNN 結構與DNN 結構，其最大的特點在于能夠將過去與未來的信息作為輸入再一次地輸入到神經元，這種結構非常適合具有時序性質的數據，但同時也可能需要更長的訓練時間。Bi-RNN 結構解決了其中較為重要的時序問題，能夠對一些有時間依賴性的數據進行更好的學習，如語音識別、情感分類、文本分類、機器翻譯、詞向量的生成等，將Bi-RNN 展開后，可看出在網絡結構中有一部分參數是共享的，這在一定程度上大大減少了所訓練的神經網絡參數個數，同時也帶來了另一個優勢——Bi-RNN 輸入可以是不固定長度的序列。因此基于傳統的RNN 計算原理，可對結構進行一定程度的改進，推導出Bi-RNN結構。Bi-RNN 可以同時利用過去與未來時刻的信息，將時間序列信息分為前后兩個方向，輸入到模型里，并構建向前層與向后層用來保存兩個方向的信息，同時輸出層需要等待向前層與向后層完成更新[16]，才能進行更新。其模型結構如圖4所示。

Bi-RNN 的整個計算過程與單向循環神經網絡類似，即在單向循環神經網絡的基礎上增加了一層方向相反的隱含層。從輸入層到輸出層的傳播過程中，共有6個共享權值。圖4中，W0表示輸入層與向前層之間的權重值，W1表示上一時刻隱含層到當前時刻隱含層之間的權重值，W2表示輸入層與向后層之間的權重值，W3表示向前層與輸出層之間的權重值，W4表示下一時刻隱含層到當前時刻隱含層之間的權重值，W5表示向后層與輸出層之間的權重值。Bi-RNN 結構向前傳播的計算過程如下列公式：

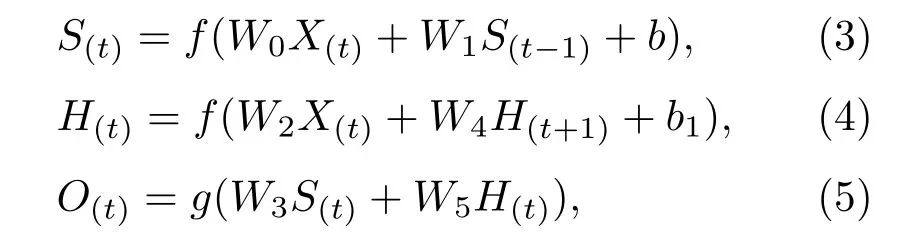
其中，X(t)表示在t時刻的輸入，S(t)表示向前層的第t個RNN 節點的輸出，H(t)表示向后層的第t個RNN 節點的輸出，O(t)表示在t時刻的輸出，b和b1表示偏置參數，f和g均表示激活函數。相對于傳統的RNN 而言，Bi-RNN 實現了同時利用過去與未來時刻的信息，因此記憶效果比之前更佳。

圖4 雙向循環神經網絡結構Fig.4 The structure of Bi-RNN

2 漢語識別實驗

2.1 實驗設計

本文基于tensorflow 深度學習平臺，使用Anaconda 軟件中自帶的spyder 編譯器進行編譯，并進行仿真實驗。共設置了3組實驗：

實驗1：為了說明Bi-RNN 在語音識別上的優越性，分別用DNN 模型與Bi-RNN 模型對不帶噪聲的訓練集進行實驗，并與文獻[17]所提出的改進CNN算法進行比較；

實驗2：為了測驗基于某一個環境訓練出的模型在不同背景噪聲的音頻識別效果，首先根據訓練音頻類型共設置了3 組實驗，每組實驗下再根據測試音頻類型分別設置3 個實驗；先用Bi-RNN 模型對3 個訓練集分別進行實驗，再基于3 種訓練集所訓練出的模型對其他噪聲類型的測試集進行實驗；

實驗3：為了研究隱含層中神經元數量對實驗效果的影響，本實驗基于Bi-RNN模型，通過調整隱含層神經元個數，設置8組實驗，再使用不帶噪聲的訓練集進行實驗。實驗流程圖如圖5所示。

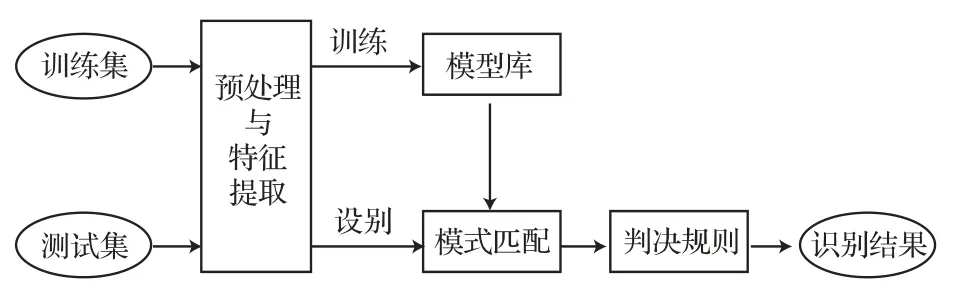
圖5 實驗流程圖Fig.5 Flow chart of experiment

2.2 數據集描述

本文采用了兩個版本的THCHS-30 語料庫：第一個是通過單個碳粒揚聲器，在安靜的辦公室環境下錄制的無噪聲音頻；第二個是通過簡單的波形混合，在第一個版本的數據加上了白噪聲和咖啡館噪聲，噪聲和音頻的能量相等。THCHS-30 的文本是從大容量的新聞選取出1000 句，音頻總時長超過30 h。參與該語料庫錄音的人員，大部分是會說流利普通話的大學生。

由于計算機性能的限制，本文沒有對整個數據集進行訓練。選用句子的發音人數目為22人，包括15 名女生和7 名男生，每句話在30 字左右，其中陳述句居多，約為95%左右。雙音素占35%左右，三音素占53%左右，單音素與四音素共占12%左右，雙音素與三音素覆蓋率較好。本文共建立了3 個訓練集以及3 個相對應的測試集，每個訓練集包括2241句話，測試集包括249句話，這3 個訓練集的差別只是在于帶噪聲的類型，其他方面設置保持一致，并且訓練集與測試集的文字內容是相一致的。

2.3 模型的構建

基于上述Bi-RNN 的優點，本文采用Bi-RNN構建模型。在文獻[18]中，DNN 的性能并不是隨著層數增加而增加的，并表明3～5 個隱層的DNN 結構是合適的。據此本文所構建的模型共包括5層，其中第1 層、第2 層與第4 層都為852 個單元的全連接層，激活函數采用ReLU；第3 層為852 維的雙向循環神經網絡，為了減小模型產生過擬合現象，在每層后面加一個Dropout 層；第5層為全連接層，并采用(X+1)個單元的Softmax 用于分類，其中X表示字體的個數，1 表示空白符號，X+1 表示字體與空白符號的概率分布。語音識別屬于神經網絡中的時序類分類，通過聯結主義時間分類(Connectionist temporal classification,CTC)來解決輸入與輸出的序列長度不等的問題。使用ctc_loss 方法來計算損失值。模型如圖6所示。

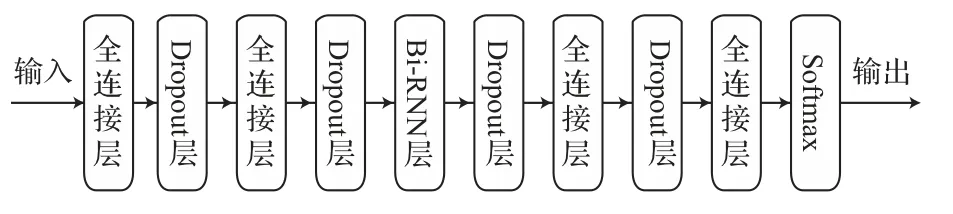
圖6 模型結構示意圖Fig.6 Schematic diagram of model structure

2.4 實驗結果與分析

實驗1

用上述Bi-RNN模型對無噪聲的訓練集進行訓練，測試集也使用無噪聲的音頻；同時對DNN 與RNN 構建模型，并采用相同的方法進行實驗，其中DNN 的模型結構是將上述Bi-RNN 模型的第3 層Bi-RNN 層換成全連接層。Bi-RNN 與DNN 實驗訓練集的損失函數值和正確率分別如圖7與圖8所示。

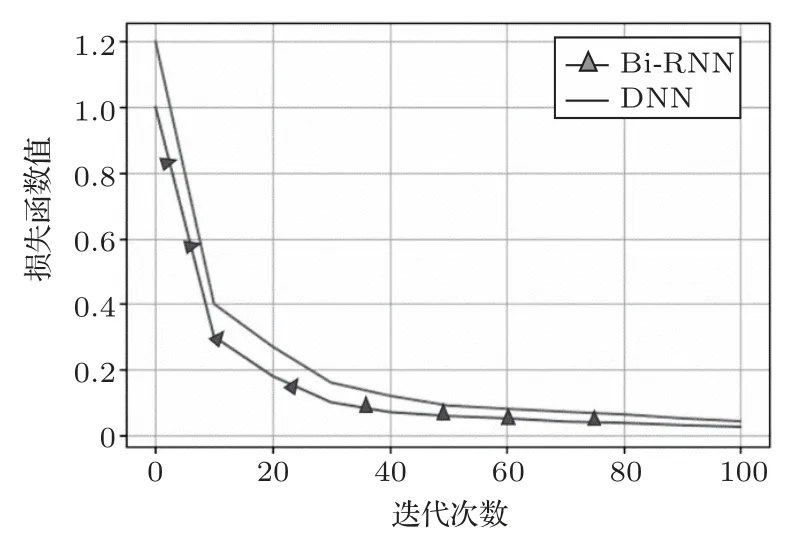
圖7 兩種不同模型的損失函數Fig.7 Loss function of two different models

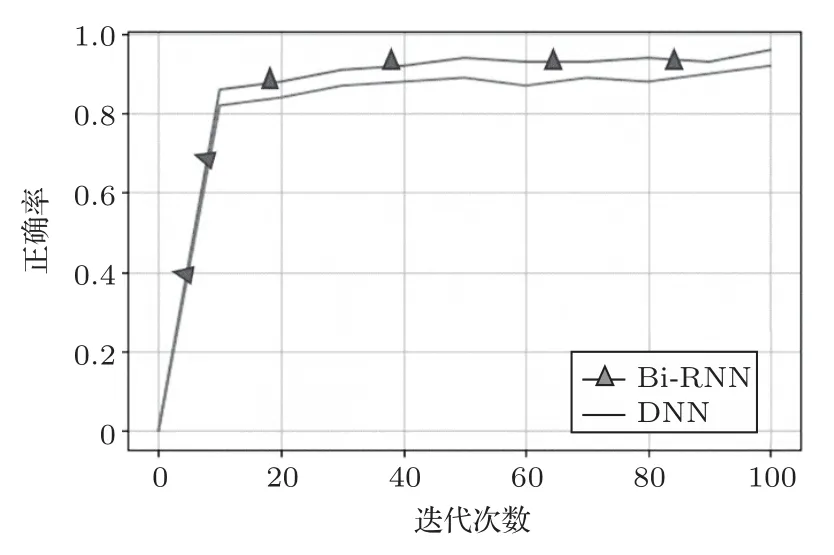
圖8 兩種不同模型的識別正確率Fig.8 Recognition accuracy of two different models

由圖7 和圖8 可以看出，Bi-RNN 模型的損失函數值下降到穩定的速度最快，且訓練集的正確率也高。兩種模型的訓練集的正確率相差不大，正確率都在93%左右。但測試集的效果顯示Bi-RNN 模型遠強于DNN 模型。在用DNN 模型進行訓練時，其在訓練集上的效果很好，但在測試集上錯誤率大大增加。從數據上表現出DNN模型產生了“過擬合”。

Bi-RNN 結構相對于DNN 結構更加復雜，Bi-RNN 對上下文相關性的擬合較強，理論上Bi-RNN相對于DNN 更應該陷入過擬合的問題，而結果顯示Bi-RNN 的識別錯誤率更低，因此單純用“過擬合”來解釋是自相矛盾的。通過對DNN的神經元進行多次調整，當神經元數量到612 時，其錯誤率最低為53.26%，相比Bi-RNN還是很高，因此并不能簡單地通過“過擬合”來解釋，說明產生這種現象根本原因在于Bi-RNN 與DNN 結構的差異性。受到協同發音的影響，語音中的各幀之間有著很強的相關性，每一個字的發音受到前后幾個字的影響。在進行輸入時，DNN 是把相鄰的幾幀進行拼接，并且其輸入窗口是固定的。而Bi-RNN 在時序問題上能夠更好地體現長時相關性，可以將過去與未來的信息同時輸入得到輸出結果，以作為預測當前的輸入，能夠更加深刻地了解其內在聯系，因此降低了錯誤率。本文又與文獻[17]所提出的改進CNN算法相比較，錯誤率也比其提出的方法較低，可見本文的Bi-RNN模型要比文獻[17]所提出的改進CNN 模型在語音識別方面性能要好。其實驗結果如表1所示。

表1 兩種模型的實驗結果Table 1 Experimental results of two models

實驗2

在現實生活中，環境因素是動態易變的。為了測試模型在不同環境下的識別效果，首先將Bi-RNN 模型在不同類型且帶噪音頻的、信噪比為0 dB 的條件下進行訓練再測試，實驗結果如表2所示。

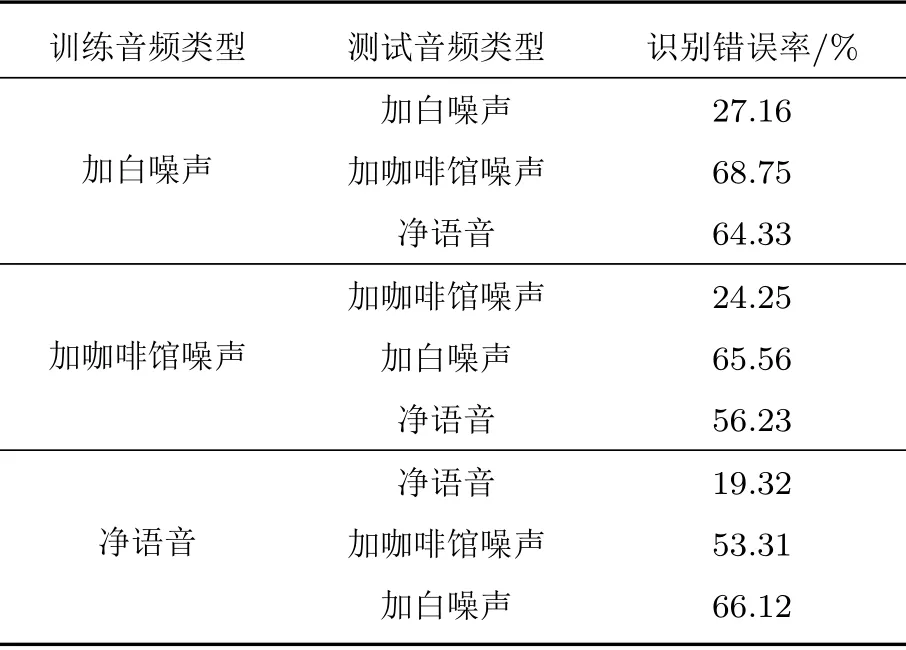
表2 基于不同音頻訓練實驗結果Table 2 Based on the experimental results of different audio training

由表2 可看出，Bi-RNN模型對3 種不同環境下的語音庫進行訓練以及測試。首先通過對表2 識別錯誤率中第1、4、7 三個數據的比較，表明訓練和測試音頻類型相同時帶有噪聲的音頻的錯誤率要比無噪聲的音頻錯誤率要高，其中白噪聲的錯誤率最高，錯誤率為27.16%，這是因為白噪聲和咖啡館噪聲同屬于加性噪聲，白噪聲屬于平穩噪聲，咖啡館噪聲屬于緩變噪聲。白噪聲是明確定義的，因為其寬帶與均勻連續特點，噪聲信號與語音信號重合度很大，導致了對語音識別影響很大，其語譜圖如圖9所示。咖啡館噪聲的頻譜分析雖和語音類似，而噪聲信號與語音信號重合度相對較小，對語音識別影響相對較小，其語譜圖如圖10所示。通過與純凈語音語譜圖(圖11)進行比較，可以看出白噪聲共振峰軌跡的干擾要比咖啡館噪聲大，因此白噪聲的識別錯誤率更高。然后通過對每組內的3 個實驗進行比較時，即當訓練音頻與測試音頻的類型不同時，其識別錯誤率大大增加，這是因為用于訓練音頻的背景噪聲與測試語音的背景噪聲不一致，訓練環境與識別環境有著巨大的差異，最終導致了識別語音特征與模板特征之間的失配，系統的性能大大降低。

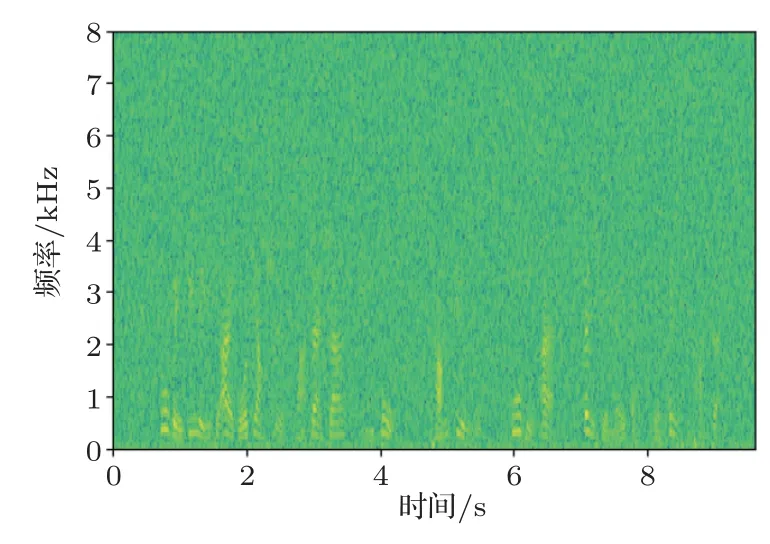
圖9 加白噪聲的音頻語譜圖Fig.9 Audio spectrum with white noise

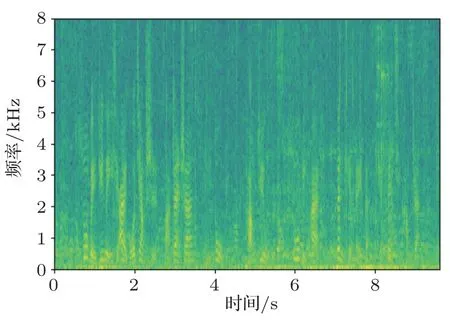
圖10 加咖啡館噪聲的音頻語譜圖Fig.10 Audio spectrum with cafe noise

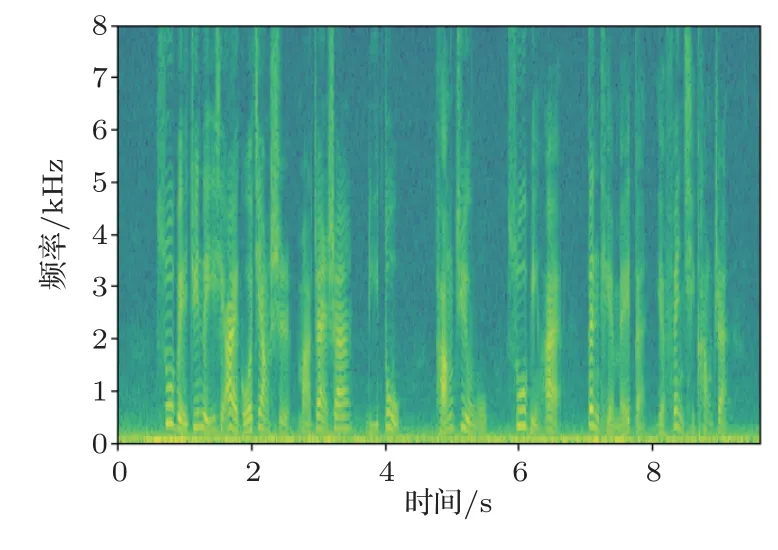
圖11 純凈音頻語譜圖Fig.11 Pure audio spectrum

實驗3

為了研究隱含層中神經元數量對實驗效果的影響，采用Bi-RNN模型，通過對隱含層神經元個數調整，進行識別。

實驗結果如表3所示，當神經元數量增加到512時，識別錯誤率大幅減少，這是因為隱含層節點數量過少，導致網絡的學習與處理能力較差；而當神經元數量大于512時，識別錯誤率的減少程度較緩，說明了神經元的數量將趨于飽和狀態；當神經元數量大于等于1024 時，錯誤率出現增加趨勢，說明再增加神經元數量，就會出現在訓練集上有很好的識別效果，但是在測試集上的識別效果變差的現象，即出現過擬合現象。

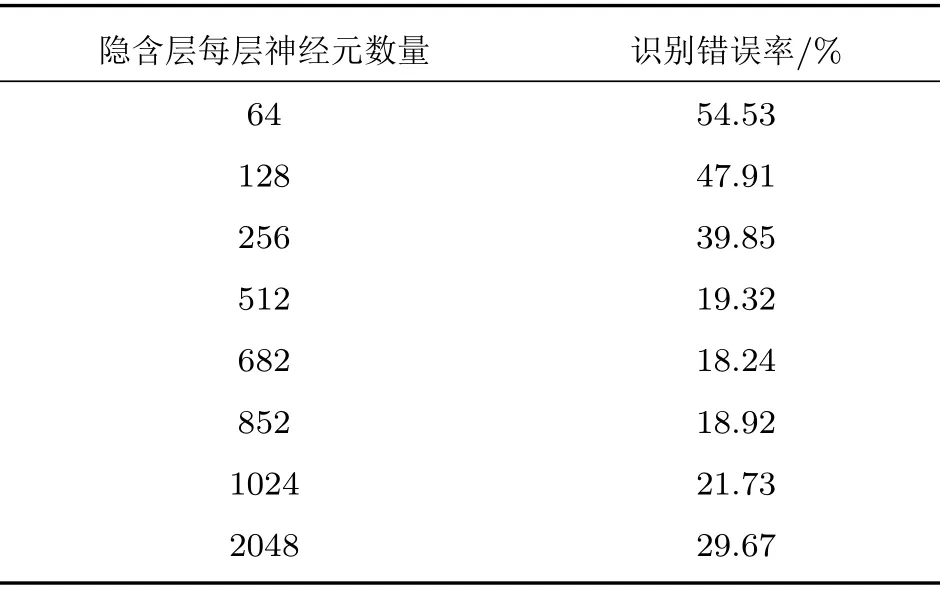
表3 不同神經元數量的實驗結果Table 3 Experimental results for different numbers of neurons

從這3 個實驗可看出，Bi-RNN 相對于DNN 在語音識別方面效果更加良好，兩個模型在無噪聲的訓練集上效果相差不大。但是在測試集上，DNN 模型錯誤率在54.76%，文獻[17]所提出的改進CNN 錯誤率在22.19%，而Bi-RNN 模型錯誤率為19.32%，相對于DNN模型與改進的CNN模型都有了降低。由此可以看出，Bi-RNN 可同時利用上下文信息，發揮出其獨特的優勢。當使用Bi-RNN模型對3 種不同類型的音頻進行實驗時，在無噪聲的測試集上錯誤率為19.32%，在帶咖啡館噪聲的測試集的錯誤率為24.25%，在帶白噪聲的測試集的錯誤率為27.16%，在無噪聲的音頻條件下實驗效果最好；當采用基于某一語音庫所訓練的模型對其他兩個環境下的音頻進行測驗時，效果很差，說明采用單個訓練集訓練的模型無法適應不同噪聲類型的音頻，在以后的研究中將考慮聯合訓練。在探索隱含層的神經元數量對識別效果的實驗中，當隱含層每層神經元數量在682～852時，效果最好。同時，識別錯誤率并不是隨著隱含層每層神經元的增加而降低，甚至當神經元個數增加到一定程度時，識別錯誤率不下降反而上升。

3 結論

自深度學習的概念提出后，深度學習在語音識別方面相較于傳統的方法，如混合高斯模型，在性能有了很大的提升。其中基于Bi-RNN 模型在語音識別方面更是具其獨特的優勢。本文使用Bi-RNN進行語音方面了探索，并與DNN和改進的CNN 進行比較，初步驗證了Bi-RNN 在語音識別方面的獨特優勢。同時對含有噪聲的音頻的識別效果進行測試，以及隱含層神經元數量對識別效果的影響方面，做了初步的探索。結果如下：(1)在漢語語音識別中采用Bi-RNN 模型得到了在同樣條件下高于DNN和改進的CNN 的識別率，成功地構建了一個漢語識別模型；(2)初步考察了噪聲對Bi-RNN漢語識別模型的影響，分析了白噪聲的影響大于咖啡館噪聲的原因；(3)研究了Bi-RNN漢語識別模型中隱含層中神經元數量對識別率的影響，提出了該模型中核心層神經元數量為682～852的最優設計。

本文由于一些軟件與硬件資源上的限制，有許多問題還需要進一步的探索。主要有：

(1)在進行探討隱含層神經元的數量對識別效果的實驗中，只是提出了神經元數量并不是越多越好，但是對不同結構的神經網絡結構神經元數量的合理設定的范圍，并未給出結果，需要進一步的探索。

(2)在本文中使用DNN 與Bi-RNN 相結合用以構建模型。在使用DNN 時，由于參數太多，易出現過擬合現象，為了更好地解決這一問題，在接下來的學習與探索中，將CNN與Bi-RNN 相結合來構建模型，并進行實驗。