面向衛星裝配的六自由度機械臂運動學分析及仿真
高 涵
(天津大學仁愛學院,天津 301636)
0 引言
目前,衛星裝配主要采用專用的工裝用于定位、支撐各個部件,然后通過人工輔助進行對接裝配。然而,人工輔助工裝存在生產效率低、關鍵對接部位可視性不強等問題,亟需一批具有快速、高精度、高可靠性的自動化裝備來滿足發展的需求。六自由度機械臂作為自動化裝備的典型代表,由于具有可靠性高、靈活性強、冗余性好等特點,在焊接、搬運、裝配及水下等領域得到了廣泛的應用[1-5]。
六自由度機械臂運動學分析是末端位姿精確控制的基礎。與正運動學問題相比,逆運動學求解較為復雜,其復雜程度與機械臂構型有關,且對于不同的機械臂構型沒有通用的解法。六自由度機械臂逆運動學求解方法主要包括解析法、迭代法及幾何法,國內外研究學者對此展開了研究。姜宏超等[6]采用解析法求解出六自由度模塊化機械臂全部逆解,雖然該方法可以求解出全部解,但求解較為復雜,計算量較大;Perez等[7]采用代數法求解七自由度機械臂逆運動學,但該方法不能保證得到有效的封閉解;李憲華等[8]根據六自由度機械臂特殊結構,采用幾何方法和解析法結合得到機械臂逆運動學完整解析解,該方法主要依賴于機械臂的特殊構型,通過幾何關系進行求解,但需要與解析法結合使用,完成逆運動學求解工作;Nearchou[9]基于遺傳算法對逆運動學問題進行了求解,但該算法的局限性在于逆運動學求解結果的收斂性依賴于初始點的選取。
針對以上問題,本文以課題組研制的六自由度機械臂為研究對象,提出一種基于牛頓迭代的逆運動學求解方法,并通過MATLAB GUI構建仿真平臺,驗證正運動學模型及逆運動學求解的可行性和準確性。
1 面向衛星裝配的六自由度機械臂正運動學分析
1.1 機械臂結構建模

圖1 六自由度機械臂三維及結構圖
本文以課題組研制的六自由度機械臂作為研究對象,其三維模型及結構如圖1所示。該機械臂由基座、肩部、肘部、手腕1、手腕2及手腕3組成,其中關節1~關節3決定了機械臂的末端位置;關節4~關節6確定了機械臂的末端姿態。為了描述機械臂關節變量與末端位姿之間的函數關系,采用Denavit-Hartenberg(D-H)建模方法構建機械臂連桿坐標系,如圖2所示;根據圖2中的結構建立D-H模型,如表1所示。

圖2 六自由度機械臂的連桿坐標系
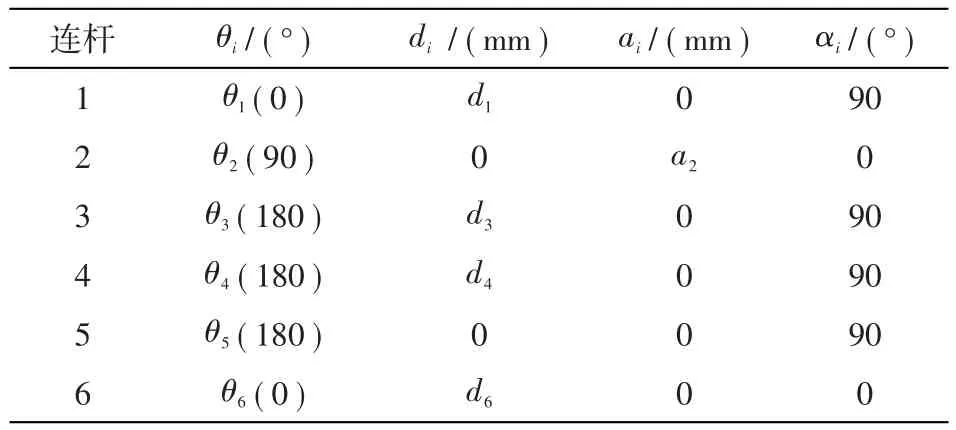
表1 六自由度機械臂連桿參數表
1.2 正運動學分析
相鄰兩連桿坐標間的齊次變換矩陣,可由公式表示為:

根據表1和式(1)即可求得機械臂末端相對于基坐標系的變換矩陣:
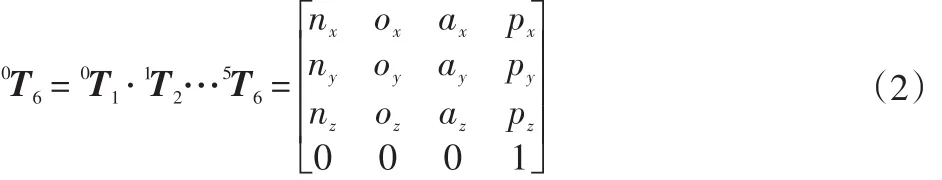
2 面向衛星裝配的六自由度機械臂逆運動學分析
由于解析法求解機械臂逆運動學計算復雜,故本文采用數值迭代法對六自由度機械臂逆運動學問題進行求解。設六自由度機械臂末端坐標系相對于基坐標系每一次迭代后得到的齊次變換矩陣為:

將式(2)和式(3)兩個齊次變換矩陣對應元素相減組成非線性方程組,由公式表示為:

將式(4)齊次變換矩陣中的12個元素分別對關節角度θi(i=1,2,3,…,6)求偏導,得到此方程組的雅可比矩陣為:

由于關節空間速度與操作空間速度存在如下關系:

式中:q˙為關節空間的廣義速度;x˙為機械臂末端執行器在操作空間的廣義速度;J為六自由度機械臂雅可比矩陣。
當時間間隔足夠短時,式(6)可改寫為:

根據式(5)~(7)即可對六自由度機械臂逆運動學進行求解,由于J(θt)為12×6階矩陣,且該矩陣為非方陣矩陣,只能對其求偽逆矩陣,每一次迭代求得的關節角度可由下式表示:
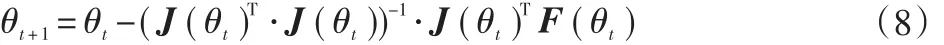
式中:θt、θt+1分別為第t次和第t+1次迭代求得的關節角度值。
基于數值迭代法求解六自由度機械臂逆運動學流程如圖3所示。首先根據初始關節角度值求解雅可比矩陣,得到下一次迭代的關節角度值;然后計算‖‖F(θ)2并判別‖‖F(θ)2是否不大于0.000 1,若滿足條件,則輸出期望位姿對應的關節角度值,否則繼續迭代,直至滿足條件為止。

圖3 數值迭代法逆運動學求解流程圖
3 六自由度機械臂運動學仿真驗證
3.1 正運動學仿真驗證
在Solidworks軟件中構建基坐標系,并按照該坐標系繪制六自由度機械臂三維模型,如圖4所示。此時機械臂各關節角度分別為0°、90°、180°、180°、180°、0°,選中末端零件的圓心,得到當前末端相對于基坐標系的坐標為(-775,23,806)mm,采用MATLAB編寫六自由度機械臂正運動學程序,并將初始關節角度代入其中,得到末端相對于基坐標系的變換矩陣為:。結果表明,求得的末端位置與繪圖軟件中得到的位置坐標一致,故構建的正運動學模型正確。

圖4 六自由度機械臂三維模型

圖5 逆運動學求解關節角度
3.2 逆運動學仿真驗證
為驗證數值迭代法求解機械臂逆運動學的有效性和可行性,采用MATLAB軟件編寫機械臂逆運動學程序,仿真中使機械臂末端沿直線運動。機械臂從(-245.821 9,210.948 5,866.207 9)mm運動到(30.6,430.3,1 000.9)mm,總運動時間為5 s,時間間隔為0.1 s,機械臂逆運動學求得的關節角度、對應的末端位置及直線運動曲線如圖5~7所示。從圖中可以看出,數值迭代法求得的關節角度連續,且不存在突變,仿真求得的關節角度對應的末端執行器位置與期望運動的位置一致,故基于數值迭代法求解六自由度機械臂逆運動學的方法是可行有效的,且機械臂末端能準確地跟蹤期望軌跡運動。

圖6 逆解對應的機械臂末端位置

圖7 六自由度機械臂直線運動曲線
3.3 仿真界面
為便于觀測求解結果情況,采用MATLAB GUI搭建了仿真平臺,如圖8所示,該仿真平臺可實現機械臂的正逆運動學求解,同時也可對直線和圓弧運動軌跡進行規劃。通過觸發課題研制的六自由度機械臂D-H參數、正逆運動學求解、逆運動學求解、直線運動及圓弧運動按鈕,可將機械臂D-H參數表、正逆運動學結果、機械臂運動曲線及關節角度曲線顯示于仿真界面中。
4 結束語

圖8 六自由度機械臂仿真平臺
以課題組研制的六自由度機械臂作為研究對象,針對解析法求解逆運動學計算量大、求解復雜的問題,提出了一種基于數值迭代的方法對六自由度機械臂逆運動學進行求解,通過每次迭代,使迭代矩陣逐漸逼近于期望位姿矩陣,并基于MATLAB GUI建立了仿真平臺,仿真結果驗證了本文所述方法的可行性和準確性。該方法也適合于其他構型的六自由度機械臂逆運動學求解,后續課題組將在此基礎上對衛星裝配機器人軌跡規劃問題展開更為深入地研究,以實現衛星裝配過程中的高效作業規劃。

