基于有限元的桿端關節軸承結構優化

摘要： 針對某型號桿端關節軸承在疲勞試驗時發生斷裂的問題，對其原結構進行有限元仿真分析，得到的最大應力位置與實際斷裂位置吻合，圓柱段仿真結果誤差與應力理論計算結果僅為0.5%，驗證仿真結果的可靠性。對桿端體各結構參數依次進行單變量有限元仿真分析，獲取各參數對桿端體最大應力和質量的影響，據此確定優化順序并對關節軸承進行優化。優化后的桿端關節軸承質量增加9.8%，最大等效應力降低14.9%，計算疲勞壽命從500萬次提高到4 600萬次，大于目標疲勞壽命值3 000萬次，優化后的樣件均順利通過疲勞試驗。

關鍵詞： 關節軸承; 優化; S-N曲線; 疲勞壽命; 有限元

中圖分類號： TH133.3;TB115.1 ? 文獻標志碼： B

Abstract： As to the failure problem of a type of rod end spherical bearing in fatigue test， the finite element simulation analysis on the original structure is carried out. The position of the maximum stress by simulation coincides with the actual fracture position， and the error between the simulation result and the theoretical calculation result is only 0.5%， which can verify the reliability of the simulation results. The finite element simulation analysis on single variable is carried out for each structural parameter of rod end body in turn， and then the influence of parameters on the maximum stress and mass of rod end body is obtained. Based on these， the optimization sequence is determined and the spherical bearing is optimized. The mass of optimized rod end spherical bearing increases by 9.8%， and the maximum equivalent stress reduces by 14.9%， the calculated fatigue life increases from 5 million times to 46 million times， which is greater than the target fatigue life （30 million times）. All of the optimized samples pass the fatigue test successfully.

Key words： spherical bearing; optimization; S-N curve; fatigue life; finite element

0 引 言

桿端關節軸承是一種安裝于桿端的球面滑動軸承，其轉動和擺動不受約束，主要承受拉、壓載荷，被廣泛應用于航空航天、工程機械和鐵路機車等領域的操縱和動力傳遞系統中。[1-3]桿端關節軸承一般包括桿端體和關節軸承2個部件，其中桿端體的主要失效模式為疲勞斷裂，關節軸承的主要失效模式為磨損。[4-6]對桿端關節軸承施加載荷譜載荷，雖然桿端體最大應力小于材料抗拉強度，但是在多次應力波動變化后，桿端體局部產生疲勞裂紋從而斷裂破壞。關節軸承磨損主要是由于軸承內圈相對外圈或襯墊轉動或擺動，導致游隙增大甚至內、外圈分離等問題，使得接觸面表面質量變差從而不滿足質量要求。某型號直升機將桿端關節軸承安裝于主旋翼控制系統中，受拉、壓載荷頻率較高，存在疲勞斷裂風險，且失效后果極其嚴重，因此對該桿端關節軸承進行結構優化，提高其疲勞壽命。

1 桿端關節軸承結構

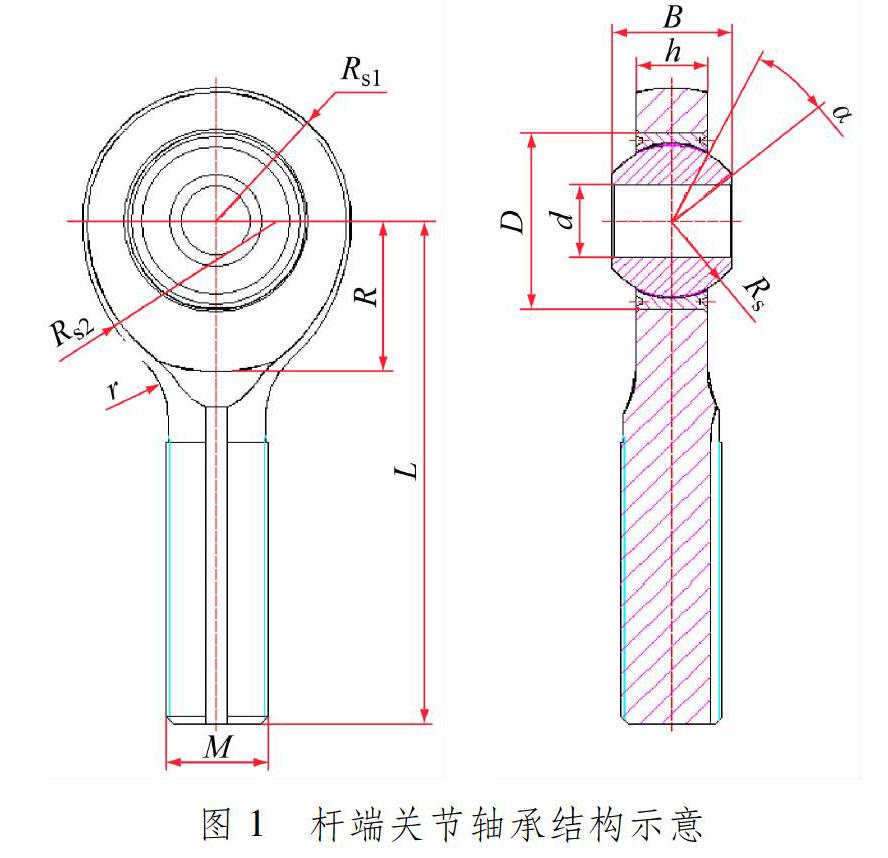
該型號桿端關節軸承結構見圖1，包括桿端體、關節軸承外圈、自潤滑襯墊、關節軸承內圈等。

根據結構特征，桿端體結構分為套圈段、螺紋段和過渡段3個部分。套圈段上半部分為Rs1球面，下半部分為以Rs2為母線的旋轉體，Rs2大于Rs1且不同心。套圈下半部分外形近似橢圓形，因此該類桿端體也稱為橢圓形桿端體[7]。M為螺紋接口直徑，L為拉桿整體長度，內圈內徑d和寬度B為銷軸安裝尺寸，α為內圈擺動角度，這些尺寸均為固定尺寸，結構優化設計中應保持不變。因為軸承內圈擺動角度α、內圈寬度B和內徑d取固定值，受軸承最小厚度和內圈端面最小厚度的約束，內圈球徑Rs和外圈外徑D的可變范圍極小，所以也取固定值。因此，影響桿端體應力分布的結構參數主要有過渡圓角半徑r、桿端體套圈上半部分球徑Rs1、桿端體套圈下半部分母線Rs2和桿端體套圈厚度h。修改這些參數進行桿端體結構優化，使桿端關節軸承在質量增加較小的前提下，獲得最大的應力減小。關節軸承外圈與桿端體鉚壓裝配對桿端體應力有一定影響[7]，但本文在同等裝配條件下優化桿端關節軸承，因此可以忽略裝配對桿端體應力的影響。

2 有限元仿真和驗證

2.1 仿真模型

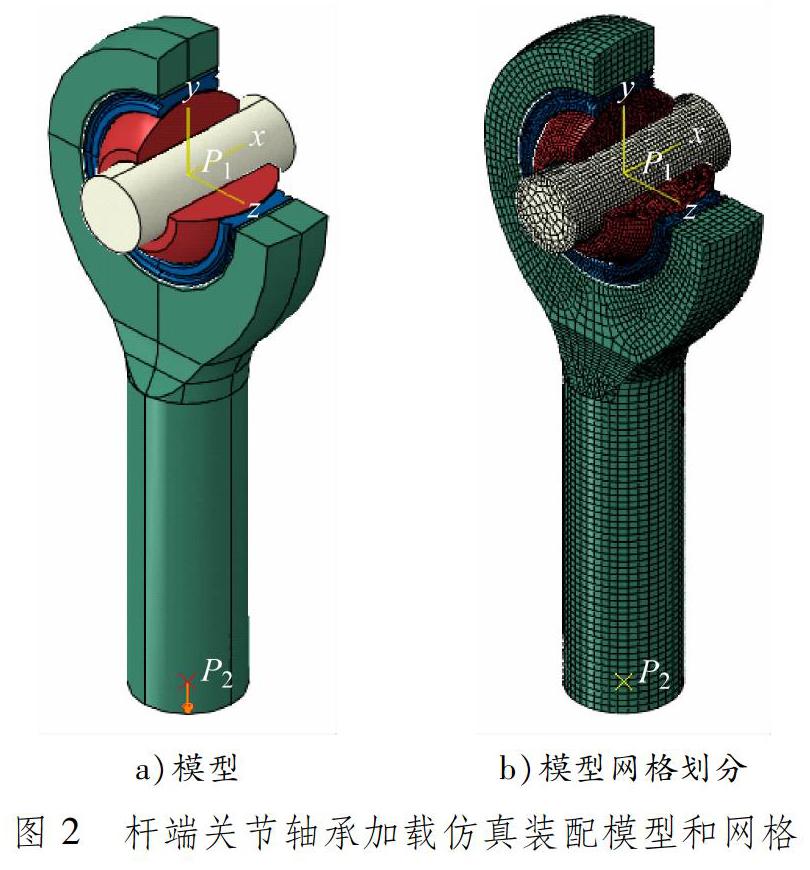
在Abaqus中建立桿端關節軸承與芯軸裝配模型，見圖2。芯軸兩端與參考點P1耦合，并在耦合點施加6個自由度固定約束。桿端體下端面與參考點P2耦合，并施加30 kN拉載荷。零部件之間接觸區域建立面-面接觸對，法向接觸屬性為硬接觸，切向接觸摩擦采用罰函數法計算。鋼對鋼的摩擦因數為0.15，鋼對自潤滑襯墊的摩擦因數為0.06。材料參數設置為線彈性材料，彈性模量為206 GPa，泊松比為0.28。模型網格僅在桿端體圓柱底部的小區域用四面體單元，其他均為六面體單元，單元總數為82 626個，并確保接觸對之間的主面單元略大于從面單元[8]。

2.2 初始關節軸承結構仿真

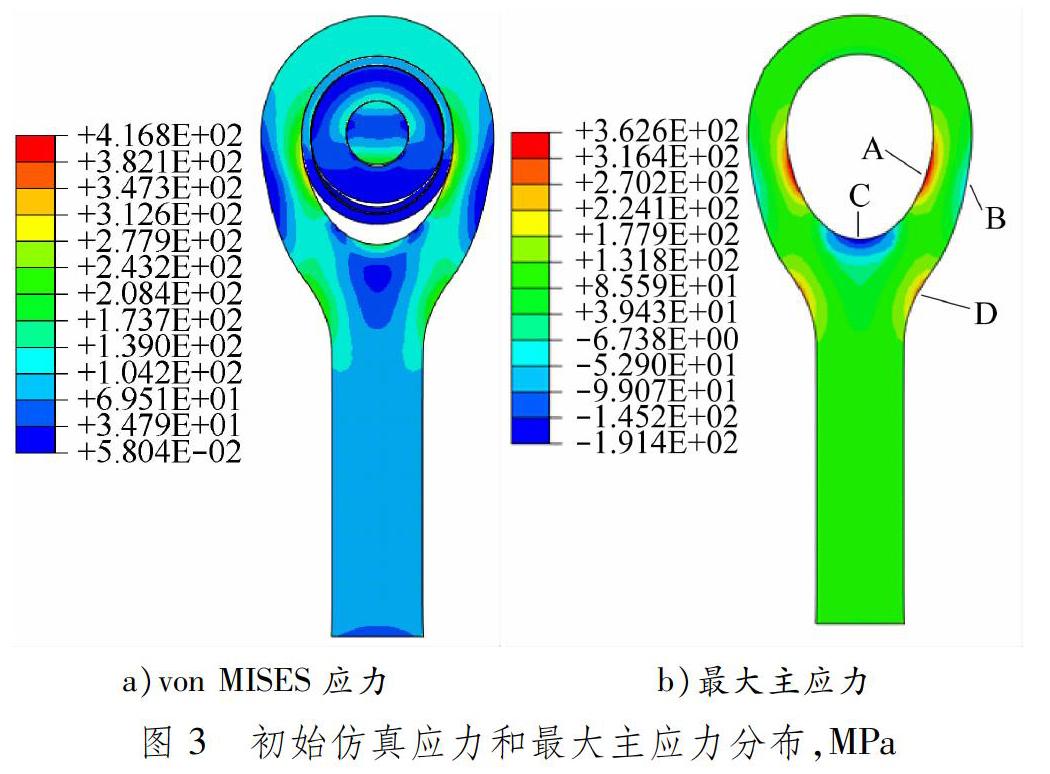
根據上述仿真模型，桿端關節軸承初始結構在拉載荷作用下的von MISES應力和最大主應力（變形量放大100倍）分布見圖3。桿端體套圈下半部分沿載荷方向被拉長，桿端體套圈內孔與軸承外圈分離產生縫隙。由于桿端體套圈由圓形被拉伸成橢圓形，桿端體套圈內孔兩側（A區域）曲率半徑增大，有被拉直的趨勢，并且此處承受拉載荷，所以該處應力最大且為拉應力，大小為354.8 MPa。由最大主應力分布可知，該處最大主應力為357.5 MPa。相反，桿端體套圈外表面兩側（B區域）隨著材料變形受擠壓，但是與此處的拉載荷相互抵消，因此應力較小。桿端體套圈內圓柱面底部（C區域）曲率半徑變小，材料受擠壓，因此為壓應力。過渡倒角（D區域）在載荷作用下曲率半徑變大，并且此處承受拉載荷，因此材料拉伸變形，應力較大。

由上述初始結構仿真結果分析可知，在拉載荷作用下，桿端關節軸承變形主要發生于桿端體，軸承應力明顯低于桿端體應力。桿端體最大應力位于套圈內孔兩側（A區域）且為拉應力，該處為桿端關節軸承疲勞壽命薄弱點，文獻[1]中桿端關節軸承斷裂分析也可驗證該結果。因此，桿端關節軸承疲勞壽命結構優化的主要任務是改善套圈內孔兩側位置（A區域）抵抗變形的能力。

2.3 仿真結果驗證

在拉載荷下，圓柱段受到均勻拉力，其理論應力σ=F/S=95.50 MPa（1） ?由圖3可知，該圓柱段應力仿真結果為95.98 MPa，仿真結果與理論計算結果誤差僅為0.5%，驗證仿真結果的準確性。桿端體套圈內孔兩側應力最大，但由于該位置在受拉載荷的同時還受彎矩載荷，該處橫截面上應力分布不均勻，很難通過理論計算獲得，因此應用有限元仿真方法進行優化。

3 有限元結構優化

不同結構參數對桿端關節軸承的應力和質量的影響不同。為分析桿端體各結構參數對桿端體最大應力和質量的影響，分別對過渡圓角r、上半圈外徑Rs1、下半圈母線Rs2、平直段長度L和套圈厚度h進行單變量多水平仿真分析。每次仿真分析時，除當前分析變量取值變化外，其他結構參數均取初始結構參數值，仿真結果見圖4。

由圖4可知，不同結構參數對軸承質量和最大應力的影響不同，且同一變量的不同取值對結果影響也不同。單變量優化可以避免多變量耦合的影響，在實際產品優化過程中還可以減少工藝變更和變量驗證等工作。但是，單變量優化無法達成目標或質量代價較大時，就需要依次優選“效率高”的變量進行優化，以最小的質量代價獲得目標應力水平。

在本算例中，根據單變量優化結果曲線可確定優化順序和優化取值依次為r=20 mm、Rs2=42 mm、L=5 mm、Rs1=27.5 mm、h=15 mm。按照上述優化次序進行優化，得到的軸承質量和最大應力結果見表1。

以單位質量可以引起的應力值減小作為優化效率，將單變量優化效率和順序優化效率進行對比分析（見圖5），兩者變化趨勢一致，優化效率依次降低。因此，根據單變量優化結果進行順序優化，可確保關鍵結構參數優先被優化。

4 疲勞試驗和分析

對初始狀態桿端關節軸承進行單向拉伸疲勞試驗，最大載荷為30 kN、最小載荷為3 kN，載荷偏差控制在2%以內，按正弦波加載，載荷頻率為4.3 Hz。疲勞試驗結果見圖6，4個桿端關節軸承試驗件在試驗過程中均發生疲勞斷裂，斷裂位置均位于桿端體套圈側面位置，與圖3仿真分析結果桿端體套圈兩側最大主應力最大相吻合。4個桿端關節軸承試驗件的平均疲勞壽命為500萬次，與產品疲勞壽命目標3 000萬次的差距很大。在不改變材料、工藝和裝配方式的條件下，為達到目標壽命要求，必須對桿端體結構進行優化。

根據文獻[9]中0Cr17Ni4Cu4Nb材料在4種工況下的高周疲勞數據，可以得到該材料的S-N曲線。由于加工過程材料組織變化、桿端體結構形狀和表面粗糙度等均可對產品疲勞壽命產生影響，因此實際產品的S-N曲線往往位于材料S-N曲線的下方。根據文獻[10]可知，材料S-N曲線與構件S-N曲線在對數坐標系下是平行的。因此，根據圖6試驗結果，通過平移材料S-N曲線，可獲得實際桿端關節軸承產品的S-N曲線，見圖7。由此可知，若要使疲勞壽命達到3 000萬次以上，則應力應減小到326 MPa。根據前文順序優化結果，當優化進行到第4步即可滿足要求。當優化到第5步時，應力為308 MPa，疲勞壽命為4 600萬次，此時質量增加9.8%、應力降低14.9%。

該型號產品經上述方法優化后，4個樣件均順利通過疲勞試驗，驗證優化的有效性。

5 結 論

在桿端關節軸承實際使用過程中，桿端體套圈疲勞斷裂是其主要失效模式之一，據此對桿端關節軸承結構進行仿真優化分析，結論如下：

（1）利用Abaqus建立桿端關節軸承加載仿真模型，由最大應力位置和圓柱段應力，可驗證仿真結果的可靠性。

（2）針對桿端體關鍵結構尺寸參數，分別進行單變量仿真分析，以單位質量對應力的影響值作為結構優化效率評價指標，認為桿端體中間過渡圓角r、桿端體套圈上半部分球徑Rs1和桿端體套圈下半部分母線Rs2的優化效率較高，結構優化時應優先改善這3個參數。

（3）根據各參數優化效率對各優化參數進行排序，并按該順序進行優化仿真，以避免參數之間的相互影響。按該順序優化時，各參數的優化效率與單變量優化時的效率變化趨勢一致。優化后桿端關節軸承的最大應力為308 MPa，比原結構降低14.9%，結構質量僅增加9.8%。

（4）基于桿端關節軸承疲勞試驗建立結構件產品S-N曲線，基于該曲線預測，實現3 000萬次疲勞壽命的應力為326 MPa，而優化結果應力為308 MPa時的疲勞壽命已經為4 600萬次，滿足壽命要求。通過優化，4個該型號產品樣件均順利通過疲勞試驗。

參考文獻：

[1] 蘇高峰， 薄玉成， 孔靜靜， 等. 桿端向心關節軸承動應力下疲勞壽命分析研究[J]. 機械設計， 2013， 30（3）： 89-92. DIO： 10.13841/j.cnki.jxsj.2013.03.027.

[2] 李旭平， 藍國水. 新型高速桿端關節軸承的壽命設計與試驗研究[J]. 麗水學院學報， 2011， 33（5）： 49-51. DIO： 10.3969/j.issn.1008-6749.2011.05.013.

[3] 齊愛霞. 桿端關節軸承三維參數化計算機輔助設計與研究[D]. 青島： 山東科技大學， 2006.

[4] 袁兆靜， 劉紅宇， 邵玉佳， 等. 桿端關節軸承桿端體的疲勞斷裂機制[J]. 機械工程材料， 2018， 42（12）： 13-17. DOI： 10.11973/jxgccl201812003.

[5] 曾坤， 張韶佳， 陳昕， 等. 桿端關節軸承失效分析[J]. 失效分析與預防， 2018， 13（5）： 318-323. DOI： 10.3969/j.issn.1673-6214.2018.05.010.

[6] 艾劍波， 黃文俊， 李滿福， 等. 直11型機尾槳變距拉桿故障分析與處理[J]. 直升機技術， 2009（3）： 68-71. DOI： 10.3969/j.issn.1673-1220.2009.03.014.

[7] 邱明， 呂桂森， 占松華， 等. 自潤滑桿端關節軸承的摩擦性能研究[J]. 兵工學報， 2013， 34（6）： 754-758. DOI： 10.3969/j.issn.1000-1093.2013.06.015.

[8] 王啟瑞. 基于Abaqus的GE17自潤滑關節軸承結構分析與改進[J]. 計算機輔助工程， 2017， 26（4）： 51-56. DOI： 10.13340/j.cae.2017.04.009.

[9] 霍金東， 由小川. 基于能量法的17-4PH鋼材疲勞特性研究[C]// 北京力學會第21屆學術年會暨北京振動工程學會第22屆學術年會論文集. 北京： 北京力學會， 2015： 374-379.

[10] 解放. 典型構件疲勞性能S-N曲線的獲取及應用[J]. 機械設計， 2015， 32（4）： 71-73. DOI： 10.13841/j.cnki.jxsj.2015.04.015.

（編輯 武曉英）