正交異性整體鋼橋面建模分析方法對比
萬波 肖林 蔡俊宇
(1.中國鐵路南昌局集團有限公司,南昌 330000;2.西南交通大學土木工程學院,成都 610031)
正交異性整體鋼橋面(Orthotropic Steel Bridge Deck,OSD)構造復雜,為深入認識整體鋼橋面的力學特性,通常將其受力分為3 個結構體系[1-2]:①正交異性鋼橋面板作為主梁上翼緣板參與主桁受力,與主桁共同構成主要受力體系;②由正交異性鋼橋面板與縱橫梁(肋)共同組成的橋面體系,主要承受橋面上的荷載;③支撐在縱橫梁(肋)上的連續各向同性的橋面板,直接承受車輛輪壓,并將其傳遞到縱橫梁上。由于各受力體系傳力復雜,采用解析法求解具有極大的難度,目前多采用數值方法建模求解。現有各種建模分析方法需要對結構進行不同程度的簡化,簡化的結果直接影響計算的效率和分析結果的精度。
為了解正交異性整體鋼橋面3種典型建模分析方法的適用性,結合某典型正交異性鋼橋面橋梁進行建模分析,并對比應力與變形分析結果,為同類橋梁設計、分析提供參考。
1 OSD建模分析方法
1.1 空間桿系法(Spatial Frame Method,SF法)
結構設計初期,需要對主要受力構件進行大量的試算以初步確定構件尺寸等參數。鋼結構橋梁在設計的初始階段,若采用耗時較長的空間板梁法進行試算,則會大大降低初始階段的設計效率。通常設計的做法是在前期選取適當的簡化計算方法進行試算,初步擬定各主要受力構件尺寸后,再用更精確的計算模型去檢算擬定的構件并作適當的微調。在設計的初期,采用SF 法[3-5]可以有效簡化計算模型,縮短設計周期。
SF 法的基本思路是:①將橋面板按一定的原則分割、合并到主梁(桁)和縱橫梁(肋)上,使其成為各主要受力構件的上翼緣;②對全橋所有構件均采用梁單元模擬,梁單元中考慮結構偏心;③由于橋面板僅是分割、合并到了不同的桿件上去,因此模型的整體剛度沒有大的變化,故求出的位移可作為實際位移;④由于橋面系荷載主要傳遞給橋面系桿件,對于非橋面系桿件,其應力可直接由所求內力計算得出;⑤對橋面系桿件,由于剪力滯效應的存在,須先確定橋面板的有效寬度,然后再計算其應力;⑥橋面板的第一體系應力可由橋面桿件上翼緣的應力插值求出,橋面板第二、三體系作用下的應力可采用單節間橋面系模型進行簡化計算。
1.2 空間板梁法(Spatial Plate and Beam Method,SPB法)
SPB 法將OSD 等效為空間梁單元與板單元的結合[6-9],其中主梁(桁)及縱、橫梁(肋)等采用梁單元模擬,橋面板用空間板單元模擬。對于一般的工字形縱橫梁,不考慮其上翼緣在梁單元的作用。梁單元與正交異性板單元共用節點或建立節點之間的耦合約束。
SPB法能充分考慮到正交異性整體鋼橋面各構件的空間相對位置,較好地反映空間剛度關系,與實際情況較為接近。在SPB 法中,橋面板的作用是傳遞荷載并參與主梁(桁)受力。一般情況下,橋面板下縱橫梁(肋)數量眾多,構造復雜,導致整個橋梁分析模型中的單元、節點主要集中于橋面系。
1.3 空間板殼法(Spatial Plate Method,SP法)
在空間板梁法分析中,板梁之間的節點連接未能考慮到節點的真實細部構造,計算結果的準確性取決于節點的支撐、約束和剛度取值,且節點的連接也較為繁瑣。在空間桿系分析法中,對于較寬的桿件,僅僅通過共用節點或約束方程連接不夠精確。此外,在以上2種模型中,也難以模擬桿件的細部構造,如橫梁與橋面板相交處開孔、橫隔板(影響桿件抗扭剛度)等。
針對空間板梁法及空間桿系法的不足,文獻[9]提出了一種基于板殼單元的空間計算方法(SP 法)。模型對所有構件均采用空間板單元進行模擬,板單元考慮了板件的薄膜效應與彎曲效應,以及與實際結構更吻合的邊界條件,能夠較好地模擬和計算鋼橋各薄壁構件以及連接部的應力分布。
2 工程實例分析
2.1 工程背景
以一座(110+2×220+110)m 鐵路連續鋼桁梁柔性拱橋為例,主桁中心距15.0 m。主桁及橋面鋼材采用Q370qE。設計荷載為雙線ZK 活載,運行速度為250 km/h。橋梁1/2立面見圖1。

圖1 橋梁1/2立面(單位:m)
該橋正交異性整體鋼橋面由橋面板、橫梁、橫肋、縱肋及I肋5個部分組成,其中鋼橋面板全橋縱橫向連續,縱向與下弦頂板伸出肢焊接,橫向分段焊接。與以往正交異性鋼橋面的縱橫梁體系不同,大橋采用密布橫梁體系鋼橋面,典型橫斷面布置見圖2。本文選取一個節間(包括兩端橫梁上翼緣外側,總長度為14 m)的正交異性整體鋼橋面為研究對象,分別采用SF 法、SPB 法和SP 法建立有限元模型進行分析,節段平面布置示意如圖3。
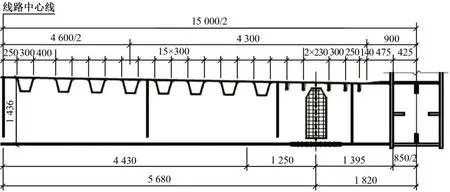
圖2 典型橫斷面布置(單位:mm)
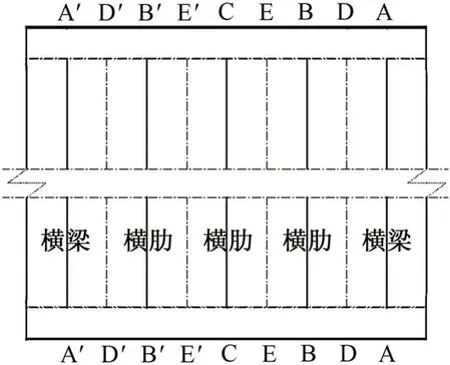
圖3 節段平面布置示意
2.2 分析模型及分析工況
SF 模型將橋面板按照有效寬度折算到橋面系桿件上,有效寬度按照文獻[10]規定計算。建立SF分析模型,見圖4。為方便模型加載,在對應實橋節段的4 個節點處施加簡支約束;為避免在弦桿施加軸向力時產生應力集中,分析模型中的弦桿均向分析節段外伸1.0 m。在橋面板對應梁單元上施加ZK 活載集中力與分布力。

圖4 SF分析模型
相對于SF 模型,SPB 法模型根據各部件受力情況的不同,將下弦、橫梁(肋)、加勁肋簡化為空間梁單元,而對橋面板采用更高階的板殼單元來模擬,從而可以更真實地分析結構的受力情況。在建立模型過程中,橋面板采用空間板殼單元模擬,下弦桿和橫梁采用空間梁單元,橫梁采用倒T形截面,把其上翼緣都放在橋面板中,下弦桿采用箱形截面,SPB法中采用梁單元模擬的桿件截面見圖5。下弦桿、橫梁以及縱向加勁肋與橋面板共節點,并通過偏移梁單元形心相對位置建立空間有限元模型。建立的SPB 模型見圖6。SPB 模型的約束條件與SF 模型相似,在考慮橋面系車輛荷載作用時,將ZK活載的集中力與分布力考慮軌道結構擴散角后,以面荷載形式施加到相應的板單元上。
在建立SP模型時,通過板殼單元模擬結構的細部構造,但是未考慮焊縫對局部構造受力的影響;各構件板厚均與實際結構一致,這樣能夠較精確計算弦桿、縱橫肋、橋面板等主要部位的應力。不過對于各構件連接處存在應力集中的區域,應力計算結果與實際結構存在一定差異。建立的SP 模型見圖7。SP 模型中約束與荷載的施加方式同SPB模型。

圖5 SPB法中所用的梁單元截面(單位:mm)

圖6 SPB模型
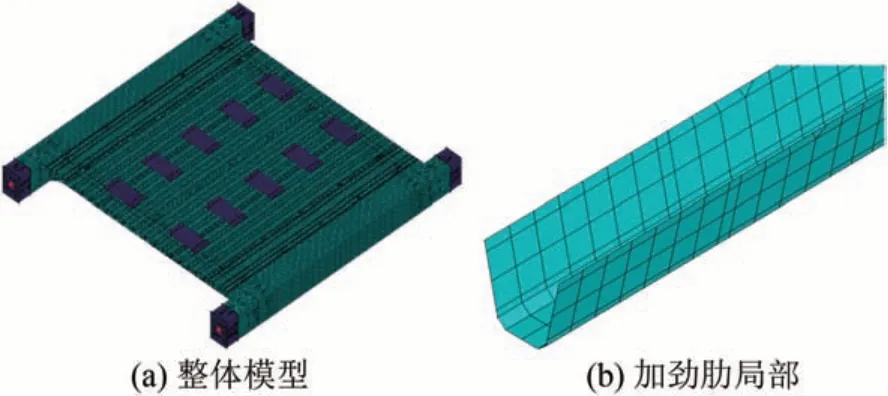
圖7 SP模型
分析荷載工況主要考慮主力作用下的弦桿軸力以及直接作用于橋面系的列車活載,包括2 種工況:①弦桿軸力及雙線中-活載作用于橫梁(肋)上;②弦桿軸力及雙線中-活載作用于橫梁(肋)間。施加鐵路雙線列車活載時,根據工況不同,在每個橫梁(肋)上或橫梁肋間面積為480 mm×1 000 mm 的區域內施加均布面荷載以模擬鐵路列車活載。
3 分析結果

圖8 工況1下不同模型的橫梁、橫肋上緣應力對比
工況1 下不同分析模型的橫梁、橫肋上緣應力對比見圖8,各橫梁、橫肋編號參見圖3。可見,各分析模型得到的橫梁(肋)的跨中應力水平相差不多,但在橫梁(肋)端部,SPB 分析模型得到的應力水平顯著大于另外2 種,甚至出現了應力值反號的情況。在SF 模型中,由于橫梁(肋)與弦桿通過節點相連,而在施加邊界條件時,沒有約束弦桿沿軸向的轉動,因此橫梁(肋)與弦桿連接節點處的負彎矩更小,得到的彎曲應力更低。
工況1荷載作用下不同模型的節段縱橫向中心線處的豎向位移對比見圖9。可見,SPB 模型得到的豎向位移顯著小于其他2 個模型。采用SPB 法時,因加勁肋截面特性計算時包括了部分橋面板,使得其剛度相對偏大。

圖9 工況1節段縱橫向中心線處的豎向位移
工況2不同分析模型中節段縱橫向中心線處的豎向位移,以及橫梁、橫肋上緣應力對比分別見圖10、圖11。工況2 的應力分析結果與工況1 類似,SPB 分析模型得到的應力水平及結構剛度都大于其他2種分析模型;SF模型中橫梁應力與SP模型相差較大。

圖10 工況2下節段縱橫向中心線處的豎向位移
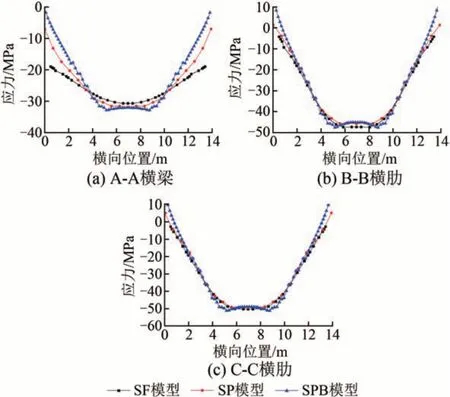
圖11 工況2下不同模型的橫梁、橫肋上緣應力對比
4 結論
采用空間桿系法(SF)、空間板梁法(SPB)以及空間板殼法(SP)對一座連續鋼桁梁柔性拱橋正交異性鋼橋面進行了分析。得到以下結論:
1)采用3種建模方法分析得到的正交異性鋼橋面受力行為較為接近。
2)3 種模型中,應用SPB 模型計算得到的結構剛度、應力峰值最大。
3)根據相關規范中有效寬度建立的SF 模型橫梁應力水平與另外2 種模型差異較大,表明其在橫梁有效寬度取值方面尚待進一步研究。在橋梁設計不同階段,可根據需求選取適當的建模分析方法。

