融合頭腦風暴思想的教與學優化算法

李麗榮，楊 坤，王培崇*

（1.河北地質大學藝術設計學院，石家莊 050031；2.河北地質大學信息工程學院，石家莊 050031；3.河北地質大學人工智能與機器學習研究室，石家莊 050031）

0 引言

教與學優化（Teaching & Learning Based Optimization，TLBO）［1-2］算法是Rao 等于2010 年提出的一種原理簡單、高效的啟發式算法。TLBO算法通過“教”和“學”兩種操作模擬了一個自然教學班中種群學習進化的過程。由于其收斂性能較好且易于實現，已經成為了群智能算法中求解全局優化問題常用的算法之一［2-5］。雖然TLBO 在數字圖像處理、背包問題、車間調度、聚類等多個領域得到了成功的應用，并展現了其優勢，但也顯現出了算法的諸多不足和弱點，如：在求解較高維度問題時，算法容易早熟、收斂速度較慢且解的精度較低等［4］。

為了提高算法的性能，克服TLBO 的弱點，國內外的專家和學者相繼提出了多種改進機制。如：該算法的創始人Rao等［6］提出了一種基于精英思想的改進教與學優化（Elite TLBO，ETLBO）算法，應用精英個體適當替換種群內的劣質個體，提高算法的收斂速度，但是該算法往往會使種群的多樣性降低較快，容易造成算法陷入局部最優。文獻［7］中提出了一種約束教與學優化算法（Improved & Constrained TLBO，ICTLBO），該算法將種群初始劃分為多個子種群，并通過種群的平均位置和子種群內最好位置之間的差異引導子種群的收斂方向，且在收斂過程中子種群間互相交換信息；在“學”階段，還引入了個體的自我學習策略，來抑制算法的過早收斂。文獻［8］中在研究對比蝙蝠算法和教與學優化算法的基礎上，提出了一種融合局部搜索的混合蝙蝠教與學優化算法（TLBO with local search and BA，TLBO-RLS），該算法將蝙蝠算法的局部搜索機制集成在TLBO的優化過程中，并應用該算法成功解決了“Team workshop problem 25”問題。Zhang等［9］提出應用對數螺旋策略和三角變異策略的思想，來解決TLBO算法容易早熟的問題。算法在“教”算子中，引入對數螺旋策略學習機制，來加快算法的收斂；在“學”算子中，利用三角變異策略進一步提高當前個體的探索和開發能力。該算法被命名為LMTLBO（TLBO with LogarithMic spiral and triangular mutation）。針對ETLBO 算法中種群多樣性降低過快的問題，于坤杰等［10］提出了一種基于反饋的精英教與學優化算法（Elitist Teaching-Learning-Based Optimization algorithm based on Feedback，FETLBO），該算法在“學”階段中增加了劣質個體與教師個體間反饋交流的機制，抑制種群的過早收斂，并通過實驗證明了算法的有效性。文獻［11］中提出了一種具有自主學習行為的TLBO（Self -Learning TLBO，SLTLBO）算法。在該算法中，種群中的個體首先執行標準的“教”和“學”兩個算子；然后，根據自己與種群內的最佳個體、最差個體之間的距離，自主完成多樣性學習，并執行基于高斯搜索的反思式學習。

上述的眾多改進機制雖然能夠較好地改善TLBO的性能，但往往需要引入較多的額外算子或機制。為了改善TLBO算法在求解高維度問題時的能力，通過引入較少的算子克服其弱點，借鑒頭腦風暴優化（Brain Storm Optimization，BSO）［12-14］產生新個體的方法，提出了一種融合頭腦風暴機制的改進教與學優化（Improved TLBO with Brain Storm Optimization，ITLBOBSO）算法。將該算法在11個無約束標準測試函數和2個有約束工程優化問題上進行仿真實驗，驗證了算法的有效性。

1 教與學優化算法的改進

1.1 基于頭腦風暴的“學”算子

頭腦風暴優化算法是近年來熱門的一個群智能算法，該算法模擬多人之間通過激烈的思想碰撞，從而產生出新方法或新策略的學習過程。從直觀上看，基于人類創新思維過程的模擬一定程度上要優于其他受動物群居行為啟發的群智能算法［15］。

教與學優化算法也是一種模擬人類集體學習行為的群智能算法，該算法具有兩個算子，分別是最優個體向其余個體執行“教”和學生之間互相“學”。前者引導種群逐漸向最優個體所在空間收斂；后者賦予種群一定的發散能力，避免算法早熟。分析BSO和TLBO兩個算法的基本原理并結合生活中的群體學習行為可知，群體內的個體通過思維碰撞提升自身狀態的效果要明顯優于個體間的相互“學”行為的效果。源于此，基于頭腦風暴機制設計“學”算子，并替換標準TLBO算法中的“學”算子。借鑒文獻［15］中的相關思想，該算子為式（1）：

式（1）中的Xr視問題的性質取min(Xr1，Xr2) 或max(Xr1，Xr2)，Xr1和Xr2為在種群內隨機選擇的個體。其他參數說明如下：

1）α∈[0.5，1)為隨機數，β=1-α。當前個體Xi生成的新狀態值取決于自身的原狀態值，以及自身與Xr的差距。以上轉換權重參數的設計是出于這樣一種考慮：“在任何學習過程中，個體Xi都有保持自身狀態的趨勢”，可以較好地抑制算法早熟。

2）Cauch（0，1）為柯西函數。由于“教”算子使算法趨于收斂，所以在這里引入柯西函數，利用其較強的變異能力保證算法具有一定的發散性，以能夠搜索更為廣闊的空間。

3）δ由式（2）計算得到，其中rand（0，1）為（0，1）內的隨機數，logsig（*）為對數sigmoid的傳遞函數，Tmax是算法的最大迭代次數，t為當前迭代次數，k是改變logsig（*）函數的斜率。多次實驗表明，k適合在［0.3，0.6］取值。分析式（2）可知δ的范圍為（0，1），且隨著迭代次數自適應變化，該參數與柯西變異結合，有利于算法早期的探索和后期的開發。

1.2 算法步驟

算法1 ITLBOBSO。

輸入：種群規模，迭代次數等參數；

輸出：最佳個體Xt(t)。

步驟1 迭代計數器t=0，在解空間內隨機生成種群pop(t)。

步驟2 計算全部個體的適應度，選擇最優個體作為教師Xt(t)。

步驟3 執行“教”算子。

步驟4 執行式（1）的“學”算子。

步驟5 算法滿足終止條件（精度要求或迭代次數滿足），則輸出最佳個體Xt(t)，終止算法；否則轉步驟2。

1.3 算法復雜度分析

設迭代次數為t，種群規模為n，分析ITLBOBSO算法，主要操作在步驟3和步驟4，兩個步驟時間復雜度均是O（n），則算法的時間復雜度為O（t*n）。使用數組存儲種群，則空間復雜度為O（n）。

2 仿真實驗與分析

2.1 無約束函數測試

應用C 語言實現算法ITLBOBSO，選擇11 個50 維的Benchmark 函數來測試該算法的性能，可接受解的目標精度為0.000 1。選擇近年來較為經典的幾個改進算法，如：ETLBO、TLBO-RLS、FETLBO、LMTLBO、DAEDTLBO［16］參與對比。ITLBOBSO 算法的種群規模d設為30，其中f1、f2、f3、f4、f5、f7、f8、f9的迭代次數為3 000，其余函數為5 000 次，斜率k=0.4。其他算法的參數設置參考各自文獻。所有算法均獨立運行30次，以消除隨機性和其他因素的影響。

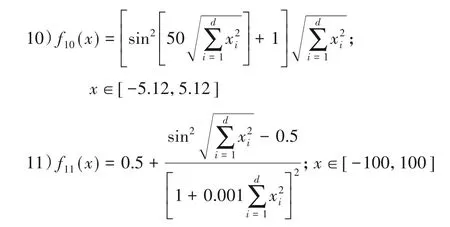
分析表1，函數f1、f2、f3、f4都是較易優化的函數，ITLBOBSO算法表現出了較好的求解能力，它在f1、f2、f3上的解均是最優的，在f4上的解略低于FETLBO 算法。穩定性的對比方面，ITLBOBSO算法在f4上略遜于FETLBO和LMTLBO，而在其他函數上則最優。函數f5為多峰，ITLBOBSO算法的表現略差，其解的質量和方差均較FETLBO和LMTLBO算法低了0.01個數量級，但仍然優于其他幾個算法。f6的解空間非對稱，對算法的搜索能力以及克服早熟的能力要求均較高，ITLBOBSO算法表現優異，無論是解精度還是解方差均超越了其他算法。在f7、f8兩個測試函數上，ITLBOBSO表現仍然優秀，解的精度是最優的，但是在f8的方差上較FETLBO 和LMTLBO 低。在函數f9上ITLBOBSO、FETLBO、LMTLBO 三個算法的解精度相當，但是ITLBOBSO 算法的解方差要稍差。f10、f11是較難優化的多峰函數，存在多個局部極值點且解空間內存在陷阱，ITLBOBSO算法表現得較為一般，解的精度均較FETLBO和LMTLBO兩個算法低，但是該算法的解方差與FETLBO、LMTLBO基本相當。

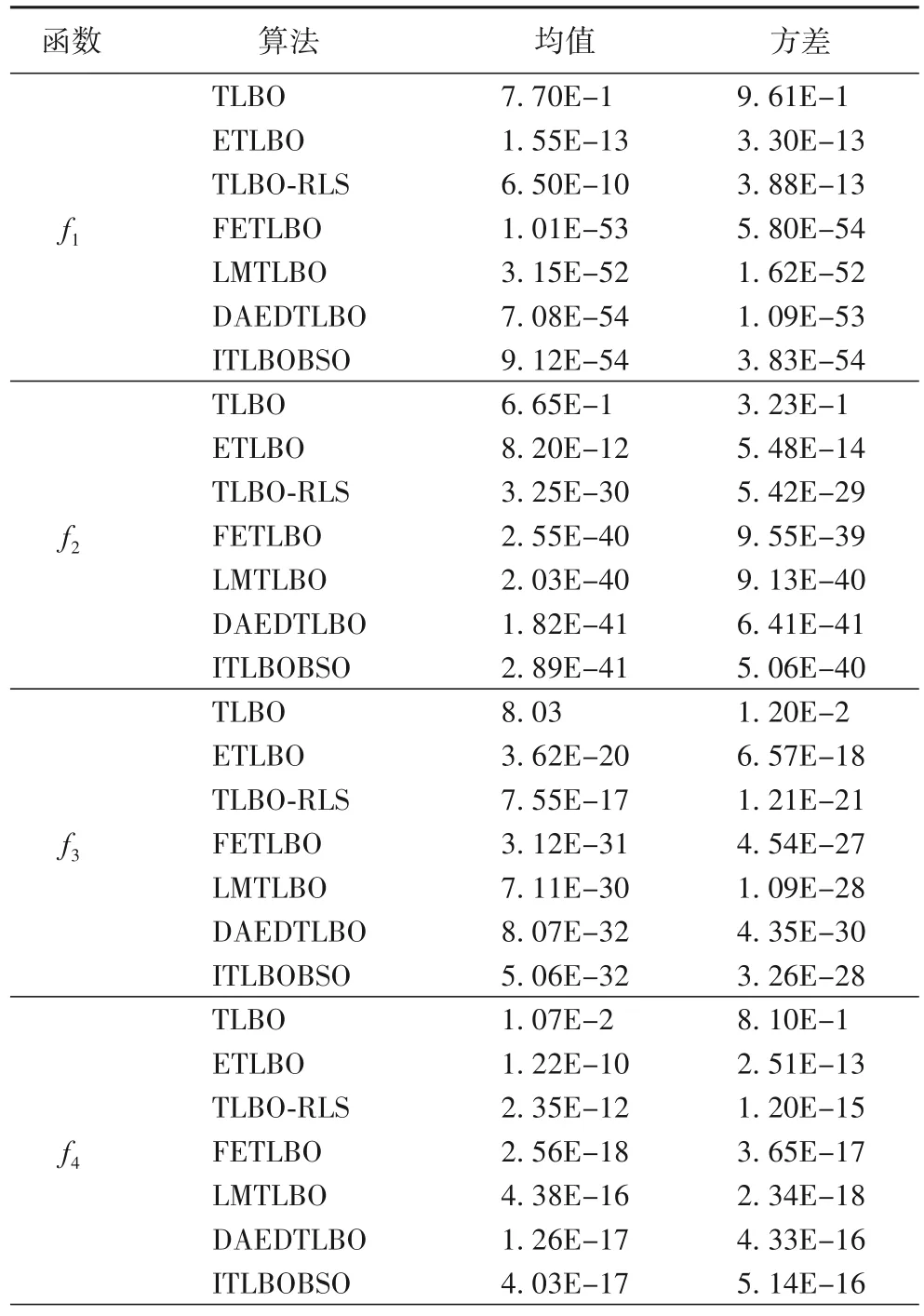
表1 無約束測試函數上的結果對比（均值/方差）Tab.1 Comparison of results on unconstrained benchmark functions（Mean/Std）

續表

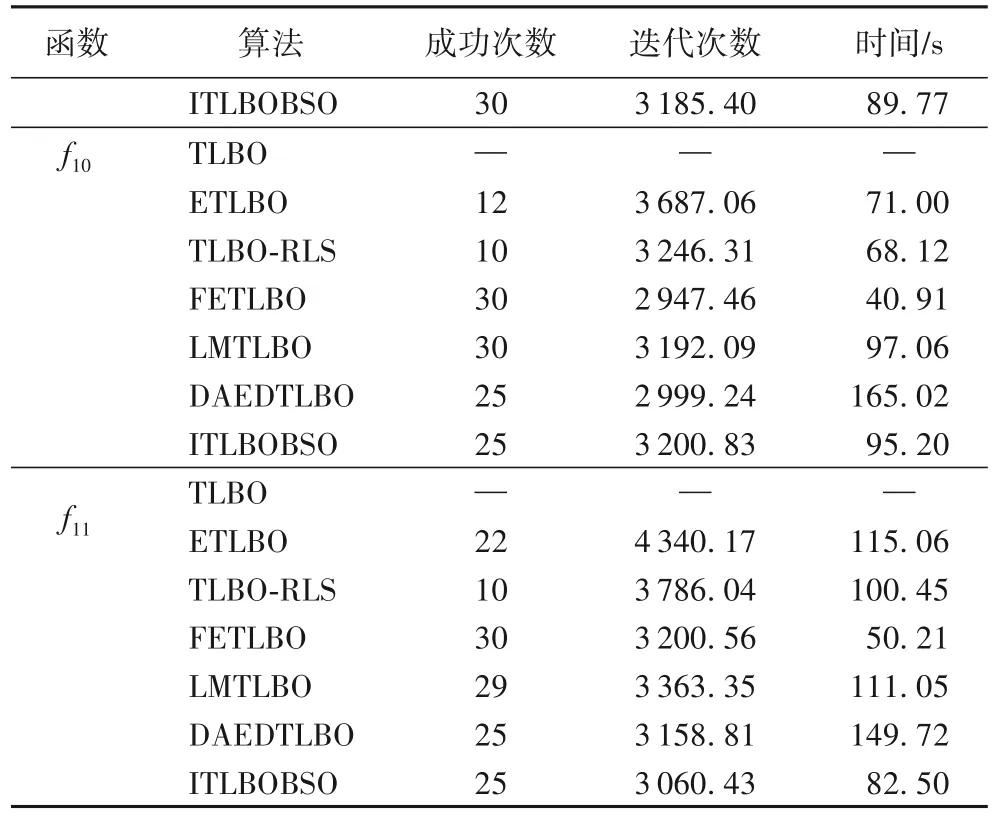
表2列出了算法的成功收斂次數（S）、成功收斂所需迭代次數（I）和運算時間（t）。從表中數據可以看出，ITLBOBSO算法在所有函數上的收斂成功次數均非常高，只是在f6、f10、f11上要遜于FETLBO或LMTLBO算法。在成功收斂所需迭代次數對比方面，本文算法在函數f1、f2、f3、f4、f6、f7、f9、f10上均高于FETLBO和LMTLBO兩個算法，在其他的幾個函數上，ITLBOBSO的迭代次數均最少。觀察對比算法的運算時間，ITLBOBSO和其他的算法均是互有勝負，但是大多數是較少的運行時間，表現比較優秀。取30次運算中最好的1次和最壞1次結果的均值，繪制了其中4個算法在f1、f2、f3、f4、f5、f6這6個函數上的收斂曲線，分別為圖1（a）～（f）。從圖中的結果可以看出，ITLBOBSO的收斂速度明顯要優于另外3個算法，在較少的迭代次數內，適應度值快速下降，使種群快速集中于最優個體周圍進行精細搜索。另外，從表1和表2中的數據可以看出ITLBOBSO解的精度以及收斂速度明顯優于DAEDTLBO算法。

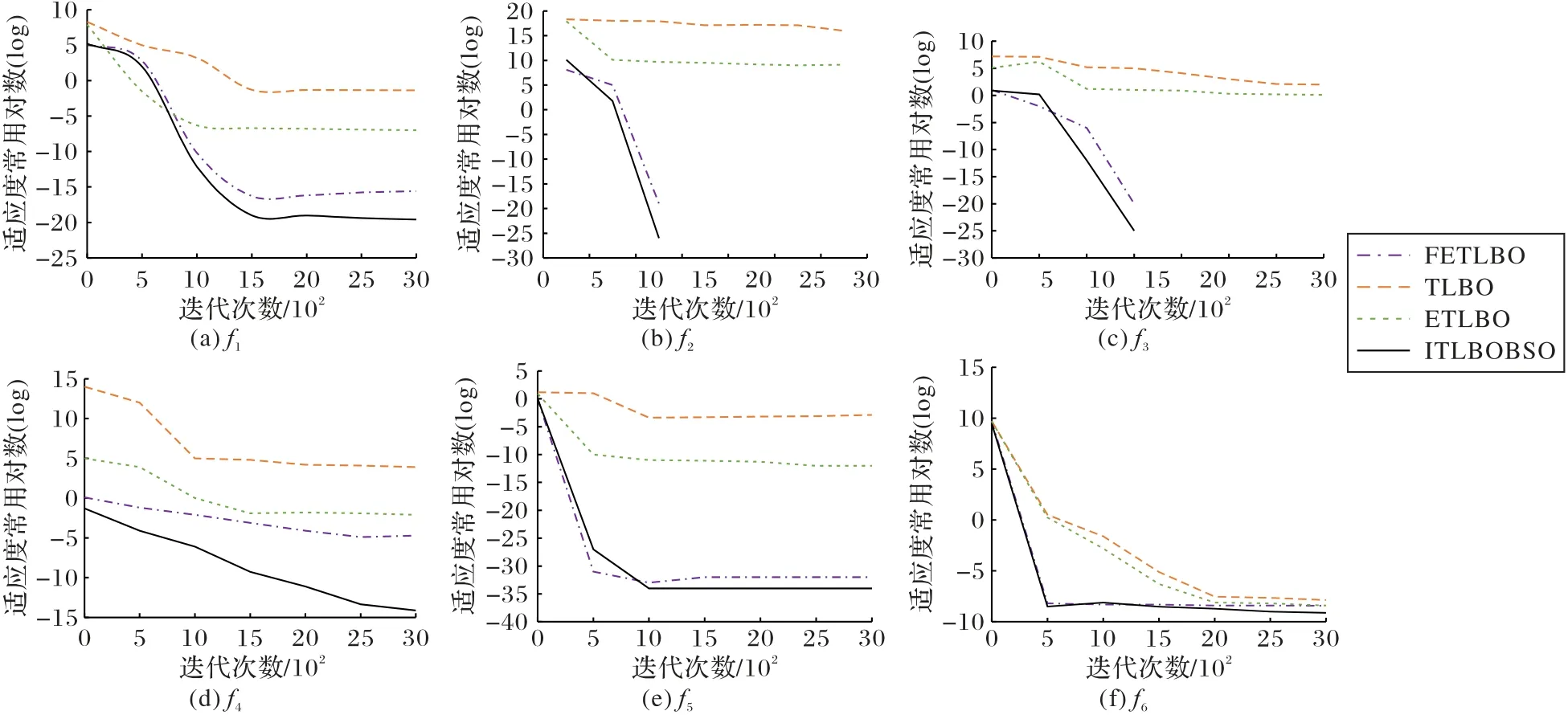
圖1 算法的演化曲線對比Fig.1 Comparison of evolution curves of algorithms

表2 無約束測試函數上的結果對比（成功次數/迭代次數/時間）Tab.2 Comparison of results on unconstrained benchmark functions（successful number/iteration number/time）

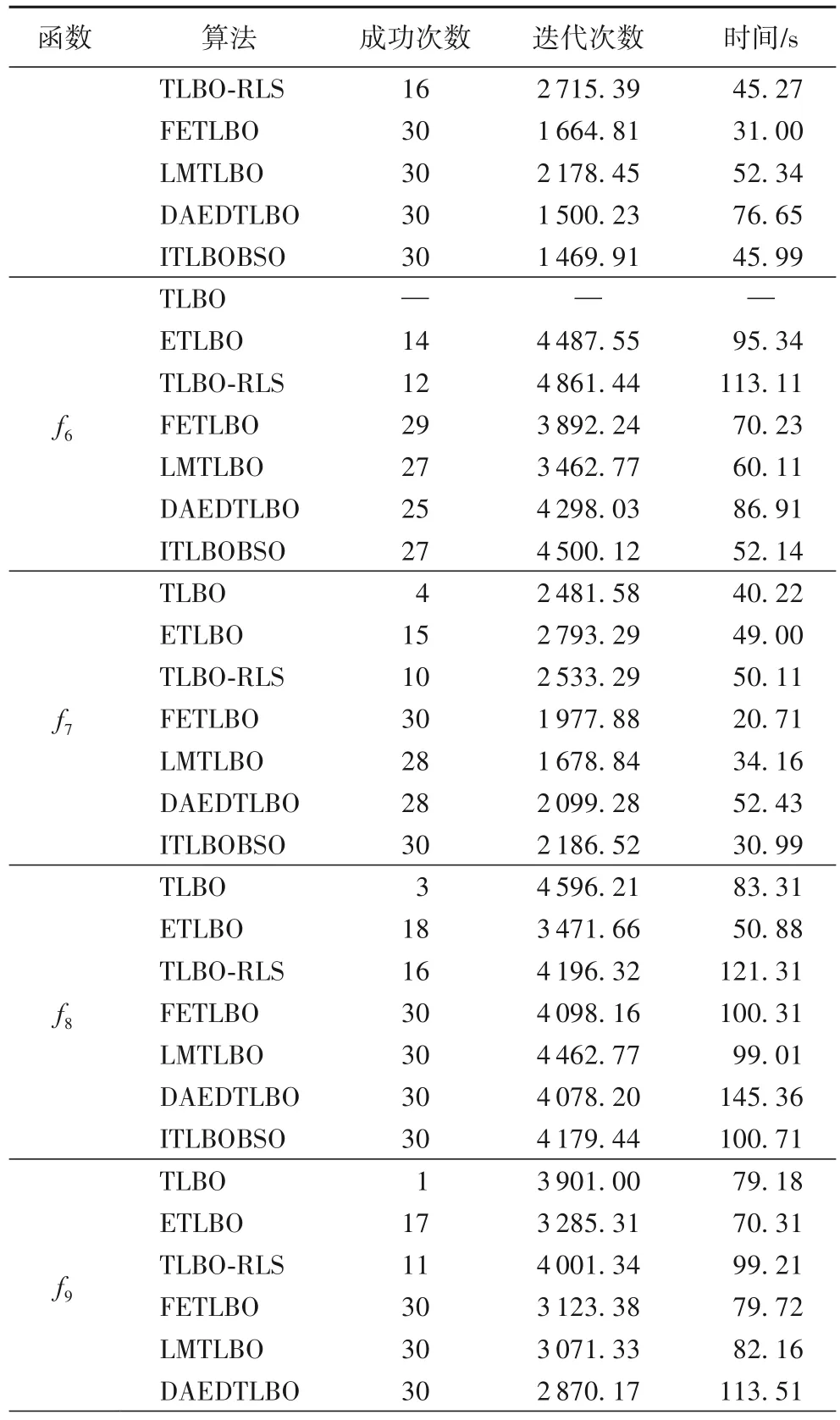
續表

續表

在算法ITLBOBSO的早期，當前個體保持向最優個體收斂的趨勢，同時由于受“學”算子的影響，個體也在不斷搜索更為廣闊的區域，避免種群過早地收斂到最優個體所在區域而使算法陷入早熟。在算法的后期，如果種群聚集在全局最優解所在區域，則個體會利用“學”算子保持自身狀態，對所在區域進行精細搜索，提高算法的解精度。如果種群被局限于局部最優解所在區域，“學”算子中的柯西函數，也會賦予種群一定的變異能力，使個體逃離約束。綜上所述，所提出算法的“教”和“學”算子可以很好地協調，保證種群全局搜索和局部勘探之間的平衡。

2.2 約束函數測試

為了測試算法在約束問題上的求解能力，選擇工程中兩個常見的優化問題：壓力容器設計優化和張力彈簧問題［17］進行實驗，兩個問題的詳細資料請參見文獻［17］。

1）壓力容器設計優化問題。

這是一個帶約束復雜結構優化問題，追求的目標是最小化總成本（含：成型代價、材料代價和焊接代價）。Ts（x1）表示半球形風頭厚度，Th（x2）為圓柱形壓力容器的溶度，R（x3）是半徑，L（x4）代表圓柱段長度。該問題的目標函數為式（3），約束條件為式（4）：

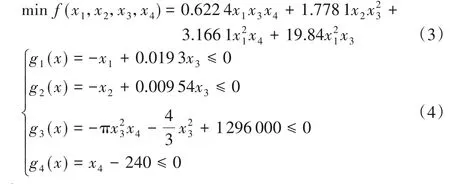
其中：1×0.062 5 ≤x1，x2≤99×0.062 5，10 ≤x3，x4≤200。

將TLBO和ITLBOBSO 兩個算法的種群規模設為50，獨立運行30 次，取結果的平均值，然后與SzAPSO（PSO with Search space zoomed factor and attractor）、SAMGA（Self-Adaptive Migration model Genetic Algorithm）、GSDE（DE with Gaussian random walk and individual Selection strategies）等算法進行對比。結果分別列于表3和表4，表中所列其他算法的數據取自文獻［17］。從表3 的數據可以看出，ITLBOBSO 算法求得的Ts（x1）、Th（x2）、R（x3）、L（x4）4 個分量以及在總成本上僅遜于GSDE 算法，明顯優于其他參與對比的算法。但是，本算法的評價次數要比GSDE少很多。

表3 壓力容器設計問題上的結果對比Tab.3 Result comparison of pressure vessel design

表4 壓力容器設計問題中的約束函數值對比Tab.4 Constrained function values comparison in pressure vessel design

2）張力彈簧設計問題。

該問題也是工程上的經典優化問題，目標是在滿足撓度、剪應力和振動頻率等約束條件下，追求所設計的質量最小。它包含有3 個變量分別是：彈簧的線圈直徑w（x1）、彈簧的平均直徑d（x2）和彈簧的有效線圈數L（x3）。該問題的目標函數為（5），約束為（6），實驗數據列于表5、6。

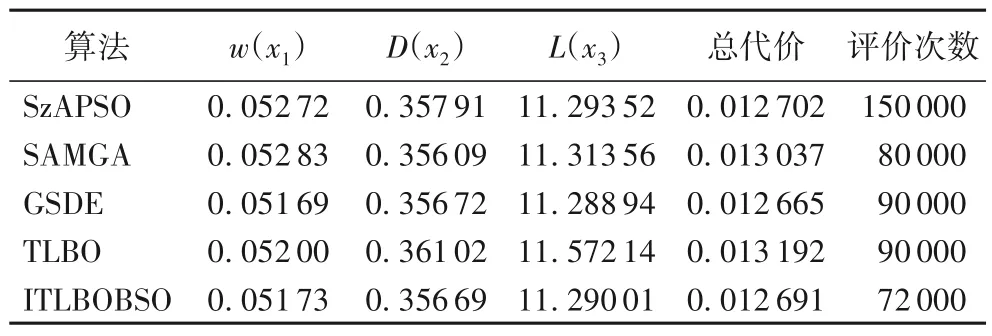
表5 算法在張力彈簧問題上的結果對比Tab.5 Result comparison of design of tension/compression springs

表6 彈簧設計問題的約束函數值對比Tab.6 Comparison of constrained function values in design of tension/compression springs

其中：0.05 ≤x1≤2，0.25 ≤x2≤1.3，2.0 ≤x3≤15.0。

從表5、6 的結果可以看出，ITLBOBSO 和GSDE 算法的表現要優于其他的算法，雖然在總代價上要稍遜于GSDE 算法，但是本算法所需的評價次數卻要比GSDE 算法少很多，說明ITLBOBSO 算法既可以保證求解的精度，收斂速度也比較快。綜合以上兩個實驗的對比結果，可知道在約束函數問題的優化上，ITLBOBSO算法具有較好的穩定性和精度。

3 結語

通過吸收BSO 算法中的優秀思想，將標準TLBO 中的“學”算子修改為基于頭腦風暴討論式的“學”算子，以期通過個體之間的思想碰撞實現種群內的信息交流和互相學習，提升種群的狀態。在新的“學”算子中引入柯西變異機制，賦予個體跳出局部最優約束的能力。選擇了11 個經典的Benchmark 函數和工程上的兩個帶有約束的優化問題進行了仿真實驗。實驗結果表明，改進算法的收斂速度、解精度和魯棒性均較標準TLBO 有明顯提升。TLBO 算法出現時間較短，也存在一些弱點，下一步將會深入研究該算法的演化原理，借鑒傳統演化算法的優點實現優勢互補。探索TLBO 算法新的應用領域也是主要的研究方向之一。