遷移學習下的火箭發動機參數異常檢測策略

張晨曦，唐 曙，唐 珂

（1.中國科學技術大學計算機科學與技術學院，合肥 230000；2.中國文昌航天發射場指揮控制中心，海南文昌 571300；3.南方科技大學計算機科學與工程系，廣東深圳 518000）

0 引言

火箭發動機是運載火箭的飛行動力核心，其組成復雜，工作環境惡劣，高頻振蕩、高溫低溫共存［1］，因此任何細小的異常在這樣的條件下都易快速發展，極具破壞性，導致發射失敗，帶來巨大損失。在航天飛行史上，因發動機故障導致的失敗次數超過總失敗次數的50%［2］。因此，對發動機的異常檢測可以幫助人們：1）在研制階段發現設計或工藝的缺陷等潛在隱患；2）在測試階段防止火箭帶故障飛行，最大限度地規避發射風險；3）在飛行階段挖掘發動機運行的異常和不足，為發動機性能優化改進提供反饋，提高航天裝備試驗鑒定能力。

目前工程應用中，常用的檢測方法以紅線法、專家系統法為主［3］，但隨著大推力火箭、可回收等新技術的應用，火箭信息化和復雜度大幅提升，這些方法顯露出了檢測誤差偏大、規則維護成本急劇增加、檢測時效滯后等局限性。近幾年來，得益于積累的海量數據，深度學習等新技術在不依賴專家知識的前提下將機器視覺、自然語言處理推向了工程化應用［4-6］。反觀航天領域，火箭型號種類多，單型號尤其是新火箭樣本有限，數據積累及共享困難，嚴重制約了目前主流機器學習技術在航天領域的應用。

對于航天領域這樣的小樣本領域，只依靠領域專家，難以快速形成評估能力，只依靠數據又缺乏大規模用于表征學習的數據集。因此本文的研究動機就是結合專家知識和數據驅動來解決傳統方法的不足，具體是以發動機為研究對象，通過領域知識構建特征空間，利用遷移學習來處理樣本規模有限導致的評估模型性能低問題。本文針對YF-75 和YF-77 液體發動機飛行任務數據，進行預處理后構建特征空間，選擇k最近鄰（k-Nearest Neighbors，kNN）與支持向量機（Support Vector Machine，SVM）兩種分類模型驗證了實例遷移、模型遷移方法對YF-77發動機參數異常檢測模型訓練和優化的有效性。

1 背景及現狀

1.1 火箭發動機參數評估內容

火箭發動機包括渦輪泵、燃燒室等部件，每個部件上安裝有不同傳感器，分別測量不同的指標（如溫度、壓力、流量），業內通常稱為遙測參數（或參數），通常一次飛行任務中與發動機有關的參數個數在2 000～2 500。

發動機工作主要有三種過程（或狀態），分別為啟動、額定工作（或滿工況）和關機過程。圖1 展示了三種過程的異常檢測步驟。

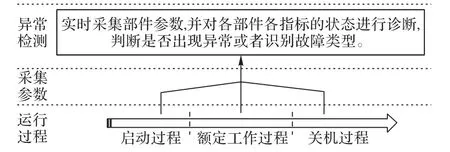
圖1 在各個過程檢測發動機參數狀態Fig.1 Checking engine parameter status in different processes

其中啟動、關機過程是十分復雜的瞬變過程，短時間內大量參數會發生劇烈變化，實踐表明發動機的大部分故障都發生在這樣的瞬變過程［7］。三類過程都有固有的關鍵指標來描述其狀態，以氧泵轉速的啟動過程為例，表1 展示了其關鍵指標、物理意義及指標異常的潛在典型故障模式。

表1 氧泵轉速啟動過程的關鍵指標Tab.1 Key indicators of oxygen pump speed in startup

1.2 參數異常檢測方法現狀

紅線法、專家系統和機器學習是火箭參數異常檢測中常用的三類方法：

1）紅線法包括閾值法和包絡法，前者是不帶時間維的理論常量區間；后者根據歷史正常數據生成帶時間維度的包絡上下限。

2）專家系統，是由火箭領域專家通過領域知識和經驗得到的狀態判決規則［8］。

3）國內從20 世紀90 年代開始至今，先后應用SVM、神經網絡和時間序列分析等方法開展對發動機故障檢測與診斷的研究［9-10］。

以上方法都有著各自的特點和適用情況。閾值法丟失了時間維，常用于檢測當前時刻的狀態，且精度不高［11］；包絡法則受樣本規模和方法本身的制約，假陽性和假陰性現象嚴重。紅線法還對噪聲敏感，難以適用于參數規模大或者樣本少等情況，檢測誤差一般較大：如果誤判會加重人工篩選的負擔，提高了人力成本；如果漏判則降低了方法可信度，增加了飛行風險。

專家系統則受制于專家知識，發動機系統覆蓋學科領域廣泛，知識表述困難。規則建立過程復雜耗時，規則質量受專家能力和經驗制約；規則對技術狀態變化敏感，導致了專家規則更新維護代價高昂。

機器學習方法則主要受制于樣本規模和質量［11］，航天領域單型號尤其新型發動機的樣本較少，而且數據的采集、分類和處理標準也不夠規范統一，導致預處理難度大，這些都嚴重阻礙了大規模的表征學習和模型訓練［2］。

2 基于遷移學習的參數異常檢測

遷移學習的目的就是設法將相近或相似領域的數據、知識等信息實現共用，一般將遷移信息的來源稱為遷移領域，將遷移信息的去向稱為目標領域，來解決目標領域樣本規模不足給模型訓練帶來的制約，從而有效解決小樣本領域應用機器學習的困境［11-14］。按照遷移的信息內容可以分為實例遷移、特征遷移、模型遷移、關系遷移［11］。目前遷移學習的有效性已經在圖像檢索、語音識別、文本分類和語義分析等領域得到充分的驗證［15-17］，在航天領域應用還處于起步階段。

YF-77 液體火箭發動機作為新型發動機，樣本規模太少，異常檢測分類模型無法進行有效的訓練，因此本文引入成熟型號YF-75發動機的樣本數據和其異常檢測模型等信息遷移到YF-77領域，實現發動機參數異常檢測，以完成火箭飛行階段的狀態監測，為指揮決策和故障診斷提供輔助的支撐信息。

在具體遷移的實踐中，將面臨如下問題：

1）YF-75與YF-77兩型發動機的相似性；

2）如何處理兩個領域之間的差異；

3）如何構建有效的特征向量；

4）選擇恰當的機器學習分類模型；

5）使用何種遷移方法。

本文將分別在2.1、2.2、2.3、2.4、3.1 節詳細論述以上問題。

2.1 兩型發動機的相似性分析

為面向現實應用需求，本文以YF-75 和YF-77 型液體發動機分別作為遷移領域和目標領域，其中YF-75 型發動機執行任務次數較多，共有352 個樣本；而YF-77 是近年研制成熟的新型發動機，目前僅有24個樣本。

根據這兩型發動機的設計原理，它們都屬于氫氧發動機，燃燒方式都是燃氣發生器循環，并且具有相同的分系統構造，主要性能如比沖、推進劑混合比等相近，二者的共有參數占YF-77 所有參數的58%，其中關鍵參數更是高達73%，且這些參數在啟動、額定工作和關機三個過程中具有相同的變化趨勢，只是在具體數值上有差別。

以氧泵轉速為例，它是專家評估發動機狀態時首要關注的參數之一，并常使用｛啟動時長，最終穩定值，（最終穩定值-起始數據值）/相應時間差，相鄰數據點斜率之平均值，相鄰數據點斜率之標準差｝五個特征值作為評價泵轉速的主要依據，記為｛T，R，d（R），E（d），S（d）｝。其樣本已經基于專家系統對其進行正常與異常的二分類標注，表2展示了兩型發動機五個特征值在正常和異常下的區間變化情況（數據經變換已脫密）。

計算兩發動機之間各特征值正常樣本區間的左邊界數值的差距除以兩個左邊界數值的平均值依次是17.74%、1.85%、6.62%、4.41%、17.16%，右邊界依次是2.11%、0.66%、1.07%、3.89%、12.40%；二者異常樣本區間的分布都明顯異于正常樣本，且各特征值異常樣本區間的左邊界差距除以兩個左邊界數值的平均值依次是9.22%、23.92%、11.35%、5.96%、20.56%，右邊界依次是6.90%、0.40%、5.47%、11.99%、7.92%。從原理、構造和數據統計的角度都說明了兩型發動機的相似性，本文還將在第3 章的實驗中充分驗證遷移的有效性。

表2 YF-75和YF-77氧泵轉速正常、異常樣本數值區間Tab.2 Value ranges of normal and abnormal samples of oxygen pump speed in YF-75 and YF-77

2.2 針對數據差異進行預處理

2.2.1 時間對齊

不同任務中各發動機的T0（發動機點火啟動的時刻）是互不相同的，為了保證各時間序列的開始時刻對齊，需要將啟動過程樣本中所有時間記錄值都減去對應的T0，使得每個樣本都以0 s為開始。

2.2.2 數據歸一化

相同類型參數在不同發動機中，其設計額定工作值可能存在差異；即使在同型號發動機的不同飛行任務中，其實際額定工作值也不完全一致。為了關注變化趨勢，本研究對每段數據樣本進行歸一化處理：對同一型號發動機，首先篩選所有啟動過程正常的參數樣本，去除噪聲后，獲取其中各樣本的最大值和最小值，分別記為MAXrated和MINrated；然后以“MINrated值轉換為0，MAXrated值轉換為1”作為縮放標準，預處理所有樣本（包括正常和異常）啟動過程的時間序列值，例如對于任意value值，它將被歸一化為：

2.3 特征空間構建

本文希望找到恰當的特征向量，它既能區分正常與異常樣本的特征，又能同時刻畫出該參數在不同領域的變化趨勢。

2.3.1 特征對正常與異常的區分性

國內研究人員曾對氫氧發動機的故障模式做出分類和仿真［1］，從已有故障模式中總結出與氧泵轉速有關的6種典型異常表征，如表3 所示，同時基于領域知識將異常表征現象與表1 中啟動過程發動關鍵指標、專家系統的五個特征值做出關聯對應。

以YF-75 型發動機氧泵轉速為例，針對每一類異常表征取一個異常樣本，同時取一個正常樣本作對比，如圖2所示。

圖2 YF-75型啟動過程氧泵轉速正常樣本與異常樣本之間的時間序列數據曲線對比Fig.2 Curve comparison of time series data of normal and abnormal samples of oxygen pump speed during YF-75 startup

為進一步驗證專家常用的5 個特征值的有效性，本研究在此基礎上，再添加｛平均值，最大值，最小值，（最大值-最小值）/相應時間差，標準差｝這些常見的統計特征，分別記作｛E，Max，Min，d（M），S｝，共組成一個10 維向量，然后進行偏最小二乘回歸（Partial Least Squares Regression，PLSR）分析，如圖3所示，得到不同特征與樣本標注的相關性。

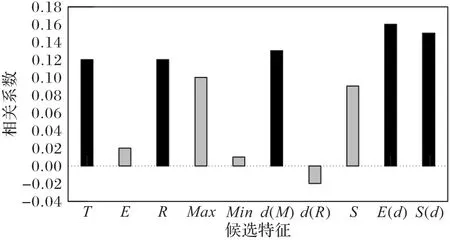
圖3 YF-75發動機氧泵轉速的PLSR結果Fig.3 PLSR results of YF-75 oxygen pump speed

表3 典型的異常表征現象及對應的啟動關鍵指標和專家特征值Tab.3 Classic abnormal representation phenomena and corresponding key indicators，expert feature values

可以看出，對于氧泵轉速而言，｛T，R，d（R），E（d），S（d）｝確實與標注結果的相關性更大；因此該特征向量滿足了物理意義和統一意義上的解釋，能夠區分正常與異常樣本的不同。

2.3.2 刻畫兩個領域的趨勢

目前仍需明確該特征向量是否能夠較好地同時刻畫出該參數在不同領域的變化趨勢，從而確定這一特征向量在遷移過程中能否有效發揮作用。首先由表2可以看出，在YF-75和YF-77 發動機氧泵轉速樣本集之間，用該特征向量表示的正常樣本區間是相似的，異常樣本區間也是相似的。

而除了這些領域專業知識和統計信息，本研究通過第3章設計的遷移實驗來驗證：如果有遷移的機器學習方法優于無遷移的機器學習方法，則可以說明這個特征向量能夠刻畫兩個領域的變化趨勢并有效地用于遷移學習中。

2.4 異常檢測分類模型

遷移學習的目的是解決傳統機器學習在小樣本領域的性能，因此依然需要選擇合適的機器學習算法，基于已有的研究［1，9］，本文選用的是kNN和SVM算法。

2.4.1kNN分類模型

kNN算法的步驟如下所示：

輸入：特征向量表示的氧泵轉速訓練樣本集、測試樣本集；

輸出：測試樣本集的kNN分類結果正確率。

1）對某測試樣本，計算與各訓練樣本的距離，按距離從小到大進行排序；

2）選取距離最小的k個訓練樣本（本文實驗中取k=3）；

3）確定前k個訓練樣本中，兩個類別的出現頻率；

4）將出現頻率最高的類別作為該測試樣本分類結果；

5）重復步驟1）～4），得到測試集的所有分類結果，與已有標注比對計算正確率。

其中kNN 算法里的距離度量使用的是標準化歐氏距離，設樣本1 的特征向量為A=（a1，a2，a3，a4，a5），樣本2 的特征向量為B=（b1，b2，b3，b4，b5），si是樣本集的第i維特征值的標準差，其二者距離d(A，B)計算公式如下：

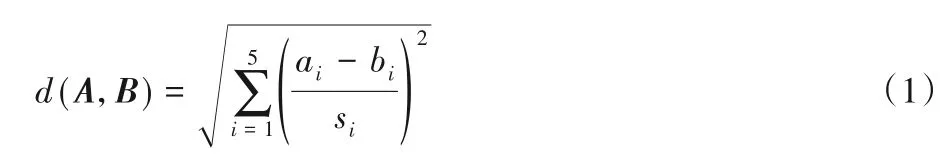
2.4.2 SVM分類模型

SVM算法的步驟如下所示：

輸入：特征向量表示的氧泵轉速訓練樣本集、測試樣本集；

輸出：測試樣本集的SVM分類結果正確率。

1）構建SVM優化函數；

2）使用SMO 算法基于訓練集求解SVM 模型的二分類分界面參數；

3）對某測試樣本，通過已建立模型計算得到分類值；

4）如果分類值大于0，則判定該測試樣本屬于第1 類，否則屬于第二類；

5）重復步驟3）～4），得到測試集所有分類結果，與標注并比對計算正確率。

設訓練樣本數量為n，特征矩陣為X=（x1，x2，…，xn），標簽向量為Y=（y1，y2，…，yn），求解滿足式（2）中優化函數的W和b，即可得到SVM的超分類平面XTW+b=0。

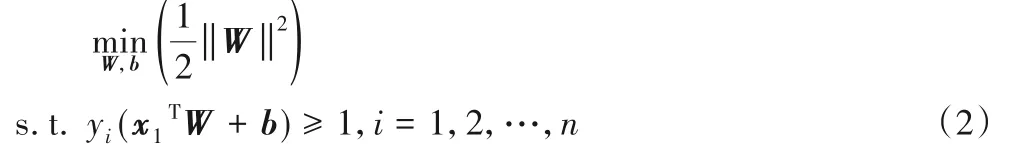
3 實驗及分析

3.1 實驗設置

待研究對象是YF-77 型發動機氧泵轉速，其樣本規模較小，是目標領域；遷移領域是YF-75 型發動機氧泵轉速樣本集，其規模較大。首先以傳統的包絡法為比較對象，驗證kNN和SVM（本文使用的訓練集與測試集均為噪聲較大的飛行實戰數據，復現的SVM 實驗精度略低于文獻［9］中采用仿真和試車數據的結果）算法在大樣本數據集中確實有優于包絡法的表現，見對照實驗1 和2；然后觀察這兩個算法在小樣本領域是否優于包絡法，見對照實驗3和4，如果并不優于，再使用遷移方法，觀測實驗5和6對比遷移是否有效。

在具體的遷移方法上，本文使用了基于實例、基于模型的遷移，其流程如圖4所示。實例遷移是將YF-75發動機氧泵轉速的樣本實例作為信息，在YF-77 模型建立前作為異常檢測分類模型的數據輸入；模型遷移是將YF-75 已經建立好的異常檢測分類模型作為信息，傳遞給YF-77領域使用；最終都需要通過測試集對比結果計算性能。

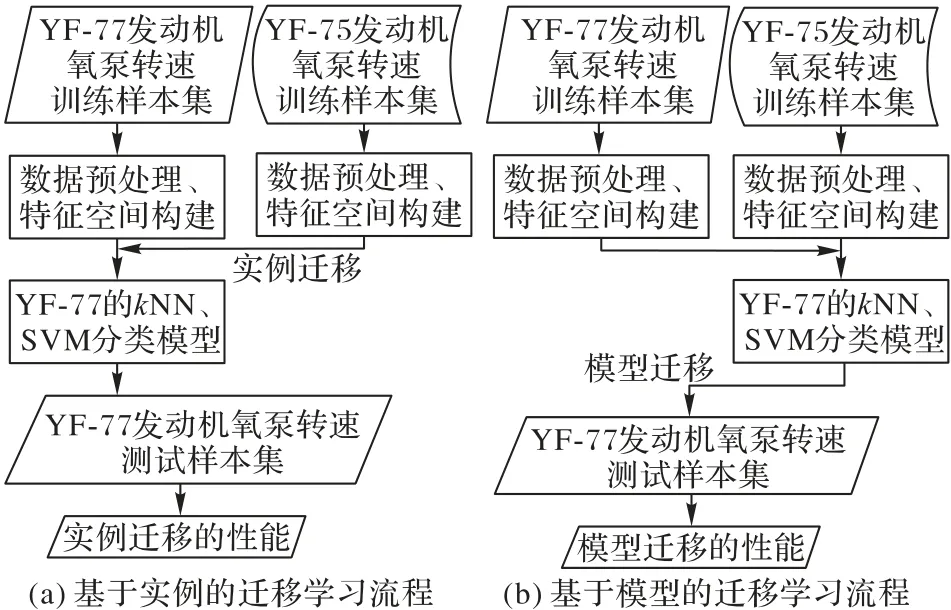
圖4 基于實例和基于模型的遷移學習流程Fig.4 Flowcharts of transfer learning based on instance and transfer learning based on model

圖5 直觀地展示了實驗設置與流程，表4 和表5 詳細介紹了各實驗組的內容。為了通過對比檢驗遷移策略的有效性，需要設定能夠合理評價模型異常檢測性能的標準。

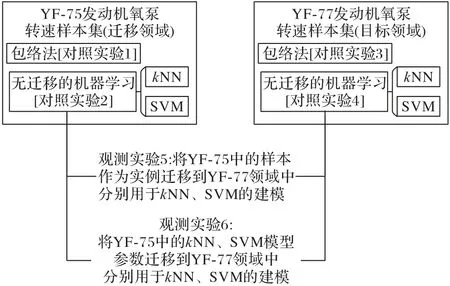
圖5 實驗設置與流程Fig.5 Experimental setting and process

為了更完備地發現所有異常狀態，希望評估系統首先盡量不遺漏任何可能的異常，同時不應隨意提示異常，否則會導致下一步耗費大量人工篩選成本。因此實驗以漏報率（Missing_Alarm）和誤報率（False_Alarm）作為“異常狀態篩選性能”的評判指標。

假設有NN個類別為Normal（正常）的樣本被分類為Normal，有AN個類別為Normal 的樣本被分類為Abnormal；有AA個類別為Abnormal（異常）的樣本被分類為Abnormal，有NA個類別為Abnormal的樣本被分類為Normal，漏報率和誤報率的計算公式分別如下：

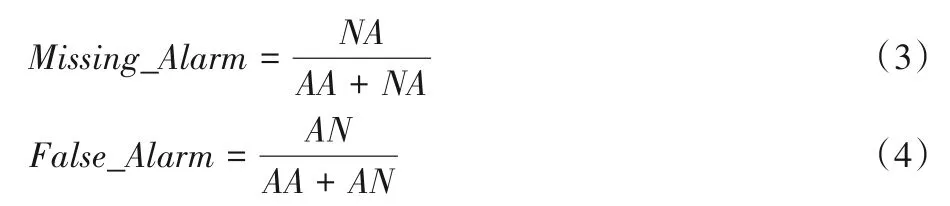
漏報率計算多少異常樣本被模型遺漏，誤報率關注多少正常樣本被模型誤認為異常。理想情況下，這兩個指標都等于零，但實際中二者是很難同時降低的，漏報率的降低一般帶來誤報率的增長，誤報率的降低往往導致漏報率的增長。綜上，對于火箭發動機而言，一個好的參數異常檢測系統，應首先滿足低漏報率，再盡量滿足低誤報率。

表4 包絡法與無遷移機器學習在不同規模數據集上的實驗設置對比Tab.4 Experimental setting comparison of envelope method and traditional machine learning on different scale datasets

表5 包絡法、無遷移機器學習和遷移學習在目標領域上的實驗設置對比Tab.5 Experimental setting comparison of envelope method，traditional machine learning and transfer learning in target domain

3.2 結果分析

實驗結果如表6 和表7 所示，通過觀察對比，由表6 可得到：

1）在包絡法中，當數據量增多時，誤報率會降低，但漏報率會增長，說明隨著標注正常樣本的增多，包絡上限會升高，包絡下限會降低，導致可能更多的異常樣本被包絡涵蓋。

2）當數據規模較大時，無遷移kNN、SVM 方法的漏報率（10.23%、12.50%）、誤報率（9.97%、9.31%），分別低于包絡法的漏報率（59.09%）、誤報率（26.88%），說明提取的特征向量可以較好體現正常樣本與異常樣本的區別。

3）當數據規模較小時，無遷移kNN、SVM 方法的漏報率（58.33%、41.67%）和誤報率（41.67%、60.83%），都比數據規模較大時相應地要高，說明無遷移的kNN、SVM方法受制于數據規模，當數據集較小時難以發揮效果。

4）即使表現最好的對照實驗2，依然存在漏報和誤報的樣本，觀察每次kNN、SVM 的漏報和誤報樣本，都處在決策邊界附近，說明當前提取的特征未能完美區分出一些特殊樣本，后續實驗可以嘗試通過修改特征權重調整決策邊界。

由表7可以得到：

5）觀測實驗5 的漏報率（14.00%、18.00%）和觀測實驗6的漏報率（12.50%、25.00%），都低于對照實驗3、4 漏報率的最小值（33.33%）；觀測實驗5 的誤報率（17.68%、13.53%）和觀測實驗6的誤報率（22.22%、14.29%），都低于對照實驗3、4誤報率的最小值（41.67%）；說明基于實例和基于模型的遷移策略都能提高kNN、SVM模型的分類性能。

6）兩個遷移學習組的漏報率和誤報率都略高于YF-75 的無遷移機器學習組，且基于實例的kNN 和SVM 表現略優于基于模型的相應方法。對于模型遷移而言，可能是沒有調整參數，下一步可以比較調整不同參數對模型遷移的影響；對于實例遷移而言，原因可能是目標領域和遷移領域樣本使用的是相同權重，下一步可以比較調整不同權重對實例遷移的影響。

7）觀測實驗5和6同樣存在漏報和誤報的樣本，其原因可能包括特征權重，以及遷移過程中的樣本權重或者模型參數。

表6 包絡法與無遷移機器學習在不同規模數據集上的實驗結果對比Tab.6 Experimental result comparison of envelope method and traditional machine learning on different scale datasets

表7 包絡法、無遷移機器學習和遷移學習在目標領域上的對比實驗結果Tab.7 Experimental result comparison of envelope method，traditional machine learning and transfer learning in target domain

3.3 結論

由實驗結果分析可以得出結論：

1）包絡法在不同量級樣本的領域中都具有局限性；

2）無遷移的機器學習方法適合大樣本集的參數異常檢測，而在小樣本領域具有局限性；

3）在數據量較少的YF-77 型發動機小樣本領域，經過時間對齊、數據歸一化得到樣本，經過特征空間構建得到特征向量后，使用基于實例遷移的kNN、SVM機器學習方法對氧泵轉速建立分類模型，在測試集的漏報率相比無遷移的kNN、SVM分別降低了44.33 個百分點、23.67 個百分點，平均34.00 個百分點，誤報率分別降低了23.99個百分點、47.30個百分點，平均35.64 個百分點；使用基于模型遷移的kNN、SVM 建立的模型，在測試集的漏報率相比無遷移的kNN、SVM分別降低了45.83 個百分點、16.67 個百分點，平均31.25 個百分點，誤報率分別降低了19.45 個百分點、46.54 個百分點，平均32.99個百分點。圖6 使用直方圖更加直觀展示了實驗結果，兩種遷移方法都比相應無遷移的方法，在漏報率和誤報率上降低了30個以上的百分點，模型性能得到較顯著的提升。

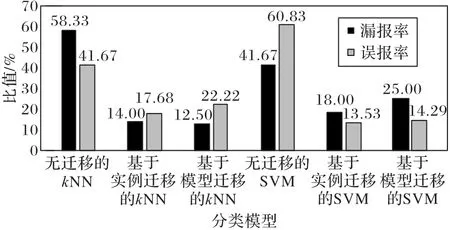
圖6 無遷移、基于遷移的分類模型漏報率和誤報率Fig.6 Missing and false alarm rates of classification models without and based on transfer

4 結語

本文探索了YF-75 與YF-77 兩型氫氧發動機之間的共性知識及可遷移性，通過構建合適的特征空間，采用實例遷移和模型遷移的方法，以YF-75、YF-77 型發動機啟動過程氧泵轉速數據集為例，通過設置四組實驗有效驗證了相比包絡法和無遷移對照，遷移對照組的kNN、SVM分類器在異常檢測的精度上得到極大提高。

雖然驗證了遷移的有效性，但仍存在如下問題亟待解決：

1）目前只關注單個參數的異常檢測，而沒有對發動機的狀態進行評估，發動機狀態是由多個參數聯合決定的，因此需要采用分層的方式提取特征，下一步將嘗試在遷移的前提下利用神經網絡來解決這一問題。

2）不同參數之間存在各類關聯，例如因果、并發、冗余關系，下一步試圖通過關聯規則挖掘來獲得參數間的關聯關系，進一步從數據的角度去發掘發動機技術特點。

3）遷移的內容還包括特征向量、特征權重、參數權重、參數關系等，下一步將研究特征、關系的遷移學習對目標領域的建模影響。