距離保持水平集演化模型的快速實現(xiàn)算法

原 泉，王 艷*，李玉先

（1.重慶師范大學數(shù)學科學學院，重慶 401331；2.重慶市中醫(yī)院藥劑科，重慶 400011）

0 引言

圖像分割是計算機視覺和其他高層圖像處理的基礎(chǔ)，也是圖像識別、配準的關(guān)鍵。它根據(jù)圖像中的灰度、紋理或形狀等特征的不同，利用這些信息將目標從復雜背景中分離出來。近些年來，大量的圖像分割方法被提出。其中，基于變分水平集的活動輪廓模型可以有效處理拓撲結(jié)構(gòu)的變化，而且能夠在分割過程中保持曲線的連續(xù)性和光滑性，近年來成為研究熱點［1-5］。其基本思想是：首先根據(jù)圖像特征為演化曲線定義一個能量泛函，為了極小化該能量泛函，常通過變分法和梯度下降法得到控制水平集演化的偏微分方程，然后用數(shù)值求解方法求解此方程，方程的數(shù)值解即為所要的分割曲線。

隨著智能信息時代的到來，醫(yī)學智能輔助診斷［6-7］、船舶導航、人臉識別技術(shù)得到了迅猛發(fā)展。對圖像分割速度的實時性要求逐漸提高，其分割速度的快慢直接影響后續(xù)圖像處理過程。例如，在醫(yī)學智能輔助診斷中，要求系統(tǒng)能夠根據(jù)掃描結(jié)果實時給出診療結(jié)果，從而輔助醫(yī)生能夠針對病灶區(qū)域進行有效的治療。然而，基于變分水平集的活動輪廓模型由于其極小化過程中所使用的梯度下降法收斂性較差［8］，導致模型分割速度較慢，難以滿足圖像分割在實際應(yīng)用時的實時性要求。

在深度學習領(lǐng)域，為了提高迭代速度，常用到動量算法（Momentum Algorithm）［9-10］、NAG（Nesterov’s Accelerated Gradient）算法［11-13］、Adam 方法［14］等。動量算法是將上一步步長的更新量取一個分量增加到當前更新的步長中，即：若當前的梯度與歷史的梯度方向一致，則當前梯度就會被加強，從而這一步下降幅度更大；若與歷史的梯度方向不一致，則當前梯度就會被減弱。NAG 算法則是在動量方法上增加一個修正的向量，防止更新得過快。該方法使得原有的梯度下降法速度有顯著的提高［11］，因此，可以使用NAG 算法代替梯度下降法，得到更高效的圖像分割算法。

本文以Li 等［1］的距離保持水平集演化（Distance Regularized Level Set Evolution，DRLSE）模型為例，提出了一種基于NAG算法的快速圖像分割方法。與DRLSE模型的原算法相比，本文算法能夠?qū)崿F(xiàn)對圖像的快速分割。在同樣的初始輪廓下，本文算法具有更快的收斂速度，迭代次數(shù)更少，分割速度更快。對于醫(yī)學圖像、紅外圖像等真實圖像不僅有較為準確的分割結(jié)果，而且分割速度較快，能夠滿足實際應(yīng)用的實時性要求。

1 距離保持水平集演化（DRLSE）模型

在傳統(tǒng)的水平集方法中，為了得到一個良好的分割結(jié)果同時使得演化曲線穩(wěn)定，水平集函數(shù)需要初始化為一個符號距離函數(shù)，而且在演化過程中需要周期性地重新初始化水平集函數(shù)為符號距離函數(shù)。這是一個復雜、耗時的過程，而且存在何時初始化以及如何初始化等問題［1］。為了避免水平集函數(shù)的反復初始化，Li 等［1］提出了一個距離保持水平集演化模型，其能量泛函定義為：

其中：μ，λ＞0，ν為常數(shù)，g(s)=(1+s2)-1為停止速度函數(shù)，H(?)是Heaviside函數(shù)，δ(?)是Dirac函數(shù)。

式（1）中，第一項為距離保持項，它使得水平集函數(shù)始終近似為符號距離函數(shù)，解決了水平集函數(shù)的重新初始化問題。其中函數(shù)p(?)稱為距離保持函數(shù)，其定義為：

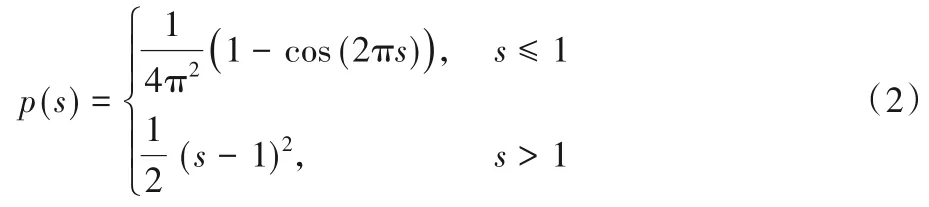
該項的提出也使得數(shù)值求解過程中允許使用較大的步長，提高演化速度。

運用變分法和梯度下降流法，極小化能量泛函，得到控制水平集演化的偏微分方程：

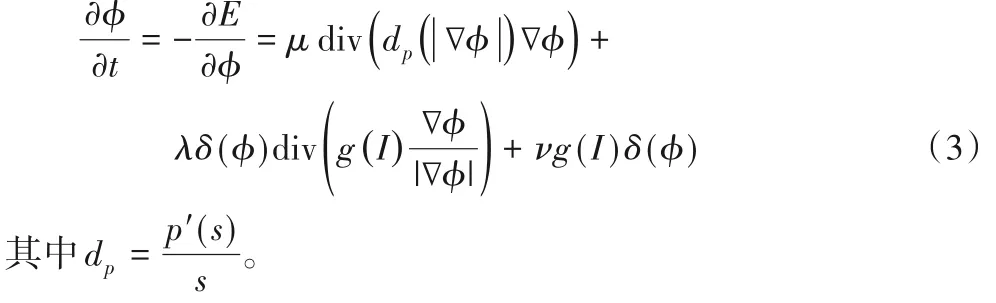
為了數(shù)值求解上述方程，用δε函數(shù)代替δ函數(shù)來近似：

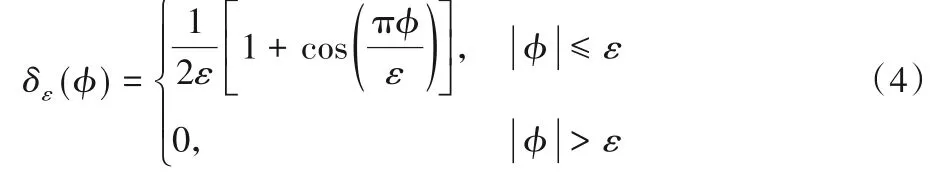
由于定義了距離保持項，演化方程（3）可以通過簡單的有限差分進行數(shù)值實現(xiàn)：

DRLSE模型在演化過程中不再需要反復初始化水平集函數(shù)為符號距離函數(shù)，極大地提高了曲線演化速度，有效地縮短了分割時間。然而，DRLSE 模型原來的數(shù)值計算方法基于簡單的梯度下降法，因此對局部極小值較為敏感，算法收斂性差，仍然難以滿足實時性的要求。后續(xù)很多模型［2-3］對其進行了改進，但大都是對能量泛函進行的。而本文是針對數(shù)值算法進行改進，目的在于提高原來算法的收斂速度，縮短曲線演化時間。

2 本文方法

用優(yōu)化的思想理解DRLSE 模型的能量泛函，就是用罰函數(shù)外點法求解一個等式約束問題的極小化，而求解極小值問題最常用的是梯度下降法。該方法使得問題的解總是朝著梯度最陡的下降方向移動，其實現(xiàn)過程中只涉及到函數(shù)一階導數(shù)的信息，因此梯度下降法能夠提供簡單快速的計算。然而，眾所周知，對于許多實際問題，梯度下降法的收斂性較差，對局部極小值較為敏感，導致到極小值點時收斂速度變慢，容易陷入局部極小值［8］。由于DRLSE模型采用了梯度下降法對能量泛函進行極小化，因此該模型也存在梯度下降法的上述缺點。為了克服這些缺點，更換能量泛函的優(yōu)化算法十分必要。

在深度學習領(lǐng)域，為了提高利用梯度下降法所得到解的收斂性和魯棒性，同時避免復雜的梯度下降優(yōu)化方法理論上的復雜性，提出了具有動量的梯度下降法，即動量算法［10］。該算法使得每次參數(shù)更新方向不僅僅取決于當前位置的梯度，還需要受到上一次參數(shù)更新方向的影響，從而加快了梯度下降法的收斂。動量算法的公式如下：

其中di和di-1分別是這一次和上一次的更新方向，g(θ)表示目標函數(shù)在θ處的梯度，β是對上一次更新方向的衰減權(quán)重，一般在(0，1)內(nèi)，α是學習率。在一次迭代過程中總的參數(shù)更新量包含兩個部分：一個是由上次的更新量得到的αβdi-1，第二個是由本次梯度得到的αg(θi-1)。

NAG 算法［11］是對動量算法的改進。該算法可以防止動量算法中解更新得過快，從而有效地避免解在極小值點處震蕩。NAG算法的公式如下：

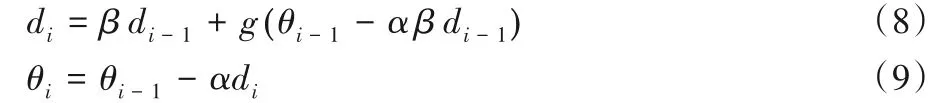
與動量算法相比，NAG 算法的梯度不是根據(jù)當前參數(shù)的位置θi-1，而是根據(jù)后一步將要到達的參數(shù)位置θi-1-αβdi-1。將式（8）、（9）進行變化，得到等效的形式：

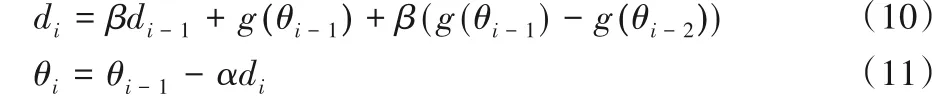
式（10）、（11）直觀地表明了NAG 算法是以下一步的梯度而不是當前位置的梯度去更新，相當于在動量算法的基礎(chǔ)上，利用了目標函數(shù)的二階導數(shù)，顯然會加速算法收斂，所以NAG 算法擁有比動量算法更快的收斂速度。NAG 算法的具體實現(xiàn)過程如下。

初始化：學習率ε，動量參數(shù)α，初始參數(shù)θ，初始速度v。

步驟1 如果達到停止準則，則算法終止；否則，轉(zhuǎn)入步驟2。

步驟2 從訓練集中包含m個樣本的小批量，對應(yīng)目標為y(i)。

步驟4 計算在臨時點處的梯度：

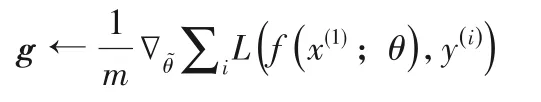
步驟5 計算速度更新：v←αv-εg。

步驟6 應(yīng)用更新：θ←θ+v。

在NAG 算法中，對θ進行不斷更新從而實現(xiàn)對目標函數(shù)的極小化。在圖像分割中，為了極小化能量泛函并最終使得演化曲線停止在目標邊緣，需要對水平集函數(shù)φ進行不斷更新。因此，水平集演化函數(shù)φ可以看作NAG 算法中的θ。NAG算法中對第k步θ的更新使用的是第k-1步的θ，而本文為了避免DRLSE模型出現(xiàn)曲線演化不穩(wěn)定的情況，對NAG算法中的φk更新步驟進行了改進，即在下述步驟5 中使用臨時更新的替代原始NAG 算法中的φk。其中函數(shù)G為式（3）中控制曲線演化的偏微分方程，動量參數(shù)α為一個常值，在演化過程中保持不變，將時間步長看作不隨著演化改變的學習率。本文算法的具體實現(xiàn)過程如下：

初始化：令時間步長為Δt，動量參數(shù)α，初始演化方程φ0，初始速度v0。

步驟1 如果達到停止準則，則算法終止；否則，轉(zhuǎn)步驟2。

步驟3 在臨時更新處計算G：

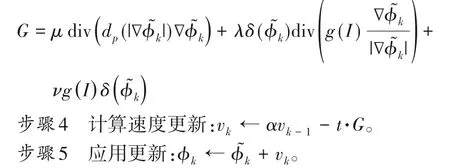
本文算法中，對演化方程的數(shù)值逼近仍采用簡單的有限差分，即式（5）中的右端項，在具體實現(xiàn)過程中按照步驟2～5 依次反復進行，并最終完成對水平集函數(shù)φ的更新。實驗結(jié)果表明，修改后的算法明顯減少了模型的分割時間。該算法實現(xiàn)簡單，易于遷移，適用于許多類型的基于水平集演化的活動輪廓模型，本文僅以DRLSE 模型為例，驗證所提算法的有效性。

3 實驗結(jié)果

本節(jié)將所提算法和DRLSE 模型原文算法應(yīng)用于DRLSE模型原文中圖像和一些具體的真實圖像，如噪聲圖像、醫(yī)學圖像和紅外圖像等。實驗結(jié)果表明，對于同樣的初始輪廓，本文所提算法比DRLSE 模型原文算法對這些圖像的分割時間和迭代次數(shù)明顯減少，分割速度更快。DRLSE 模型取與本文算法同樣的迭代次數(shù)時無法將目標從背景中完全分割出來。在所有實驗中，對于兩個模型共有的參數(shù)，為了保證實驗結(jié)果的統(tǒng)一性取值同文獻［1］一致，即λ=5，μ=0.04，Δt=5，ε=1.5。本文中的動量系數(shù)α∈(0.5，1)，具體取值在每個實驗中給出。

實驗平臺為運行Windows 10 的PC（Intel Core i5-7200U CPU 2.50 GHz 2.71 GHz，8.00 GB 內(nèi)存），程序編寫使用Matlab R2016b。

3.1 DRLSE模型原文中的圖像

圖1 給出了兩種算法對3 幅DRLSE 模型原文中的圖像的分割結(jié)果。第1、3和5行為DRLSE 原算法的分割過程，第2、4和6 行為本文算法的分割過程。第1 列給出的是原始圖像和初始輪廓，第2～4 列為分割過程，最后一列為分割結(jié)果，分割時間在圖下標注。對于這三幅圖像，本文算法中α取值為0.6，0.9，0.8。

3.2 應(yīng)用舉例

圖2 給出了3 幅噪聲圖像在兩種算法達到穩(wěn)定分割狀態(tài)時的分割結(jié)果與迭代次數(shù)。圖2（a）是原始圖像和初始輪廓，圖2（b）為DRLSE 模型原算法與本文算法同迭代次數(shù)時的分割結(jié)果，圖2（c）、（d）分別為DRLSE模型與本文模型（α取值為0.8，0.6，0.8）的分割結(jié)果。

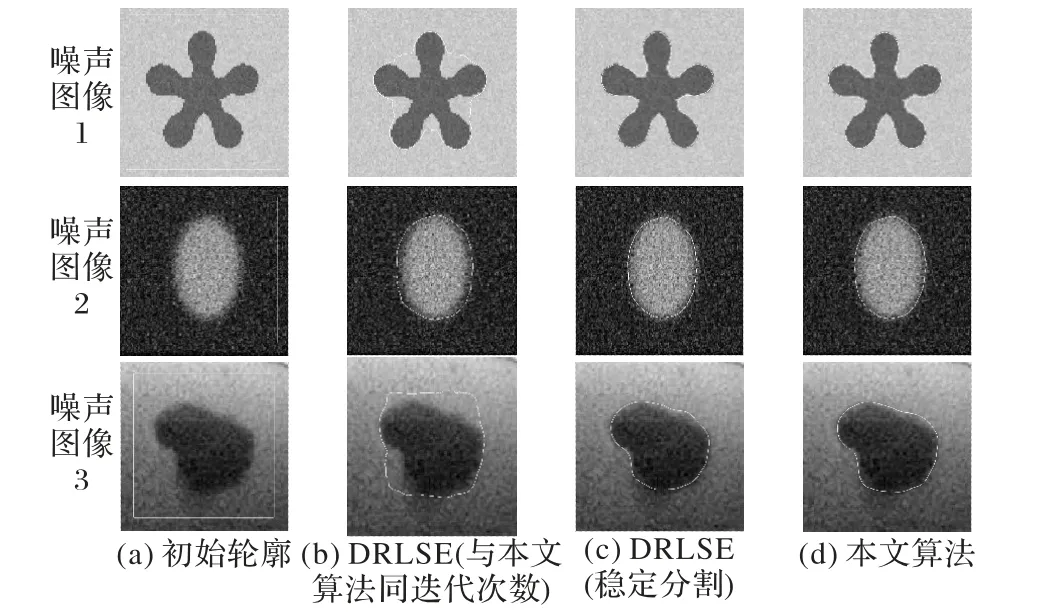
圖2 兩種算法對噪聲圖像的分割結(jié)果Fig.2 Segmentation results of two algorithms for noise images

兩種算法對應(yīng)的迭代次數(shù)和CPU 運行時間見表1，粗體顯示兩者中較優(yōu)的結(jié)果。實驗表明，本文算法比DRLSE 模型原文算法迭代次數(shù)分別減少了44%、25%、30%，CPU 運行時間分別減少了46%、31%、26%。

圖3給出了兩種算法對3幅邊緣模糊、伴有較多噪聲且背景昏暗的紅外圖像的分割結(jié)果。第1列給出的是原始圖像和初始輪廓；第2列為DRLSE模型與本文模型同迭代次數(shù)時的分割結(jié)果；第3、4列分別為DRLSE模型與本文模型（α取值為0.9、0.9和0.5）的分割結(jié)果。

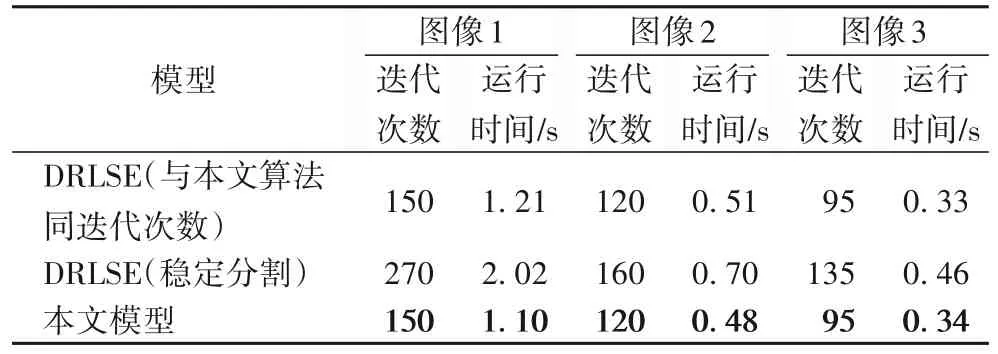
表1 兩種算法對圖2中圖像的迭代次數(shù)和CPU運行時間Tab.1 Iteration numbers and CPU running times of two algorithms for images in Fig.2

圖3 兩種算法對紅外圖像的分割結(jié)果Fig.3 Segmentation results of two algorithms for infrared images

兩種算法對這3幅圖的迭代次數(shù)和CPU運行時間見表2，粗體標注的是兩者中較優(yōu)的結(jié)果。實驗結(jié)果可以看出，本文算法比DRLSE模型原文算法迭代次數(shù)分別減小了54%、34%、33%，CPU運行時間分別減小了37%、37%、39%。

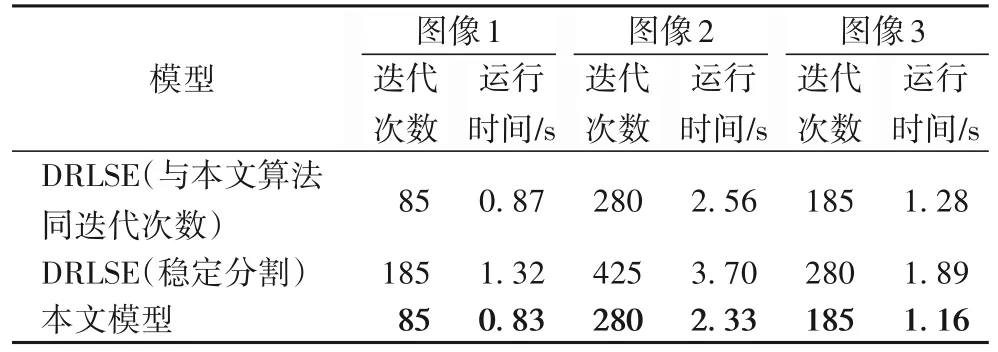
表2 兩種算法對圖3中圖像的迭代次數(shù)和CPU運行時間Tab.2 Iteration numbers and CPU running times of two algorithms for images in Fig.3

圖4 給出兩種算法對1 幅細胞分裂圖像和2 幅皮膚損傷圖像的分割結(jié)果。

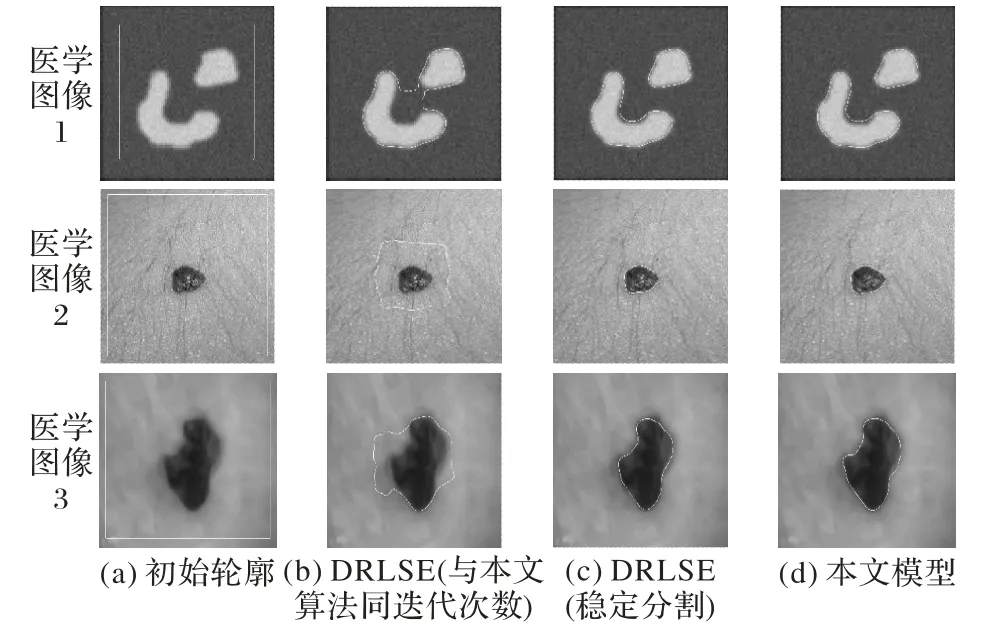
圖4 兩種算法對醫(yī)學圖像的分割結(jié)果Fig.4 Segmentation results of two algorithms for medical images

皮膚病圖像的特征是具有復雜的背景且目標具有不規(guī)則性。兩種算法的迭代次數(shù)和CPU 運行時間見表3。可以看出，本文算法（α取值分別為0.8、0.9 和0.9）與DRLSE 模型原文算法的分割結(jié)果基本相同，但本文算法比DRLSE 模型原文算法迭代次數(shù)分別減少了38%、40%、52%，CPU 運行時間分別減少了33%、50%、47%。

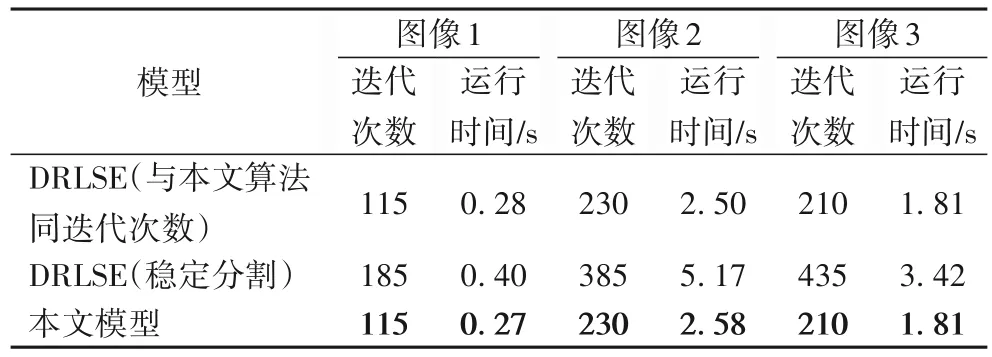
表3 兩種算法對圖4中圖像的迭代次數(shù)和CPU運行時間Tab.3 Iteration numbers and CPU running times of two algorithms for images in Fig.4

3.3 定量化評價

為了對本文所提算法的分割結(jié)果進行客觀評價，選取Weizmann 分割評估數(shù)據(jù)庫進行量化分析。實驗圖像為三幅有代表性的圖像（花、魚和飛蛾，其中α取值分別為0.5、0.8、0.6），采用F-Measure（FM）［15］以及峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）［16］作為評價標準，其定義分別為：

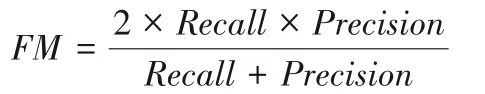
其中：Recall=，這里TP、FP和FN表示判斷為正類的正類數(shù)（True Positives），判斷為負類的正類數(shù)（False Positives）和判斷為正類的負類數(shù)（False Negatives）。FM越大說明分割效果越好。

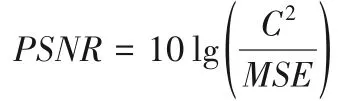
其中MSE=，C為目標和背景之間的差別，圖像的大小為M×N，I和I′是需要測試相似程度的兩幅圖像。PSNR 是衡量一幅圖像與另一幅圖像相似程度的指標。PSNR的值越高，說明兩幅圖像的相似性越高。

從表4 可以看出，在相似的分割結(jié)果下，本文提出的改進NAG 算法有較快的分割速度，能夠在有效保證分割結(jié)果的情況下，使得運行時間減少60%左右。

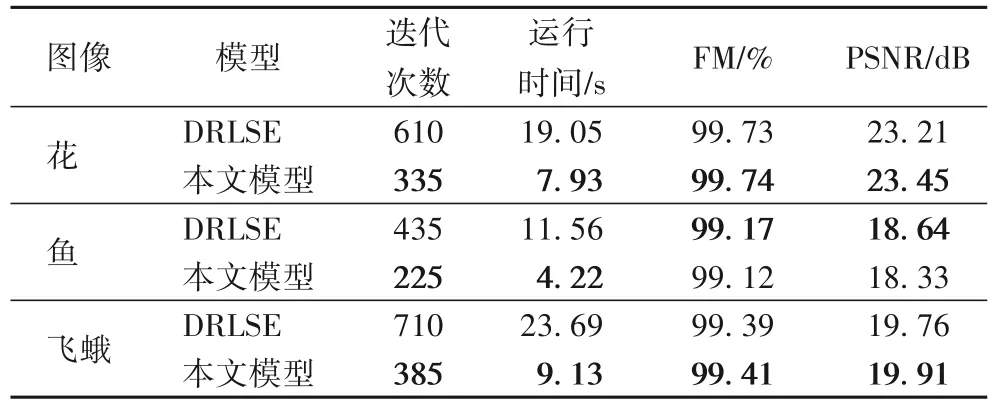
表4 兩種算法對圖5中圖像的分割效果對比Tab.4 Comparison of segmentation effects of two algorithms for images in Fig.5

為了進一步驗證本文算法與DRLSE模型在達到相似的分割結(jié)果情況下，分割速度更快，對圖5 中的三幅圖的分割過程進行收斂性分析，曲線收斂曲線如圖6所示。橫軸是CPU運行時間，縱軸為PSNR值，PSNR值越高說明兩幅圖像的相似程度越高，即分割結(jié)果越好。虛線代表的是DRLSE 模型在分割三幅圖像時的曲線收斂情況，實線代表的是本文算法的曲線收斂情況。可以看出，本文算法在更短的時間內(nèi)達到了較好的分割結(jié)果，而且有效地減少了迭代次數(shù)，提高了分割速度。

圖5 標準數(shù)據(jù)集中圖像分割結(jié)果對比Fig.5 Comparison of segmentation results of images in standard dataset

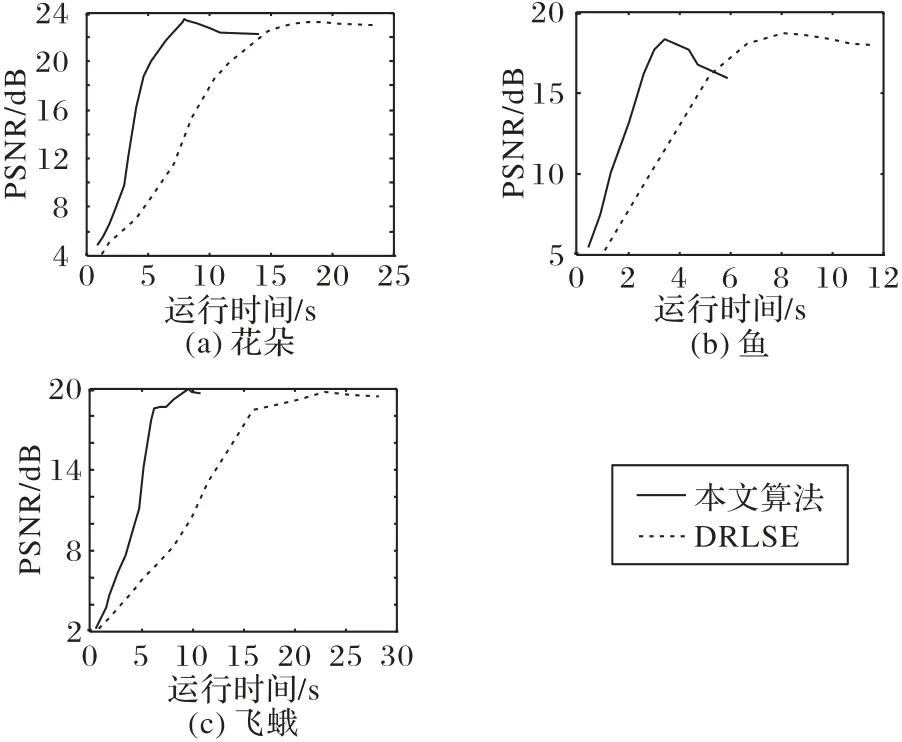
圖6 圖5中三幅圖像的收斂性分析Fig.6 Convergence analysis of the three images in Fig.5

4 結(jié)語

本文基于NAG 算法提出了一種DRLSE 模型的快速實現(xiàn)算法。實驗表明，基于NAG算法的DRLSE模型能有效地減少分割時間，減少迭代次數(shù)，提高分割速度。對于實時性要求較高的紅外圖像、噪聲圖像和醫(yī)學圖像等，所提算法不僅可以得到準確的分割結(jié)果，而且分割時間縮短為原來的一半。如何有效地處理尖角、深凹區(qū)域等是今后接下來需要重點考慮的問題。本文所提方法在基于邊緣的模型上都有推廣價值。