基于改進Gabor特征幻影的低分辨率人臉識別

卞加祁，胡學龍*，陳舒涵

(1.揚州大學 信息工程學院，江蘇 揚州 225127；2.揚州大學 人工智能學院，江蘇 揚州 225127)

0 引言

近年來，監控攝像頭的應用頗為廣泛，人臉識別系統備受重視。由于攝像頭常處于非可控狀態，故所拍攝得到的人臉圖像一般分辨率較低且質量較差。如何提高此類低分辨率人臉的識別準確率具有重要的現實意義。目前，低分辨率人臉識別主要有超分辨率重建[1-6]和穩健特征提取[7-10]。超分辨率重建算法主要是先對低分辨率樣本進行超分辨率增強，然后再進行識別。具體可以分為以下幾類：基于流形學習、基于字典學習以及基于回歸學習。在基于流形學習中，先假設高分辨率人臉和低分辨率人臉中具有相同的局部鄰域結構，在這種假設下，可以通過鄰域樣本重建生成與低分辨率人臉相對應的高分辨率人臉；具體的流形思想有：局部幾何結構以及稀疏鄰域嵌入。在基于字典學習中，通過尋找和從低分辨率人臉和高分辨率人臉特征空間有關的稀疏編碼系數來預測高分辨率人臉；基于字典學習的方法大致有2類：正交字典[3]和過完備字典。在基于回歸學習中，首先通過高低分辨率人臉數據集，建立一個映射函數，再通過這個映射函數，來構建與低分辨率人臉相對應的高分辨率人臉。具體方法有核回歸[5]、支持向量回歸等。在超分辨率重建算法中，Pong等[11]提出了一種基于Gabor特征重建的低分辨率人臉識別，即先用局部線性回歸建立一個映射函數，再通過這個映射函數，來構建高分辨率(HR)的Gabor特征；將預測得到的HR特征和低分辨率(LR)特征投影到GCCA[12]空間中，進行識別分類。

在該算法中存在一些不足：① 使用局部線性回歸(LLR)[13]預測高分辨率人臉的Gabor特征，忽略了高低分辨率之間的非線性，本文采用流形學習中一種LLE[14]的算法預測高分辨率人臉Gabor特征，有效地預測了高分辨率人臉的非線性特征；② 通過Randomized CCA來揭示高低Gabor人臉特征的非線性關系，取代了原論文中使用GCCA僅能表示數據集之間線性關系的不足。

1 Gabor特征幻影

1.1 Gabor小波

Gabor小波與人類視覺系統中的簡單細胞刺激響應非常相似。它在提取目標的局部空間和頻率信息方面具有良好的特性。Gabor小波能夠提供良好的方向和尺度選擇特性，而且對于光照變化并不敏感，能夠提供對光照變化良好的適應性，正是這些良好的特征，所以能夠被廣泛地應用于視覺。本文的人臉特征提取采用Gabor小波方法。在空間域中，由高斯函數調制的復指數構成，其公式為：

(1)

式中，(m，n)為人臉像素的位置；ω為復指數的徑向中心頻率；θ為Gabor小波的方向；σ為高斯函數的標準偏差。

1.2 高分辨率Gabor特征預測

Pong使用了局部線性回歸的方法來預測高分辨率Gabor特征，這雖然能夠在一定程度上預測高分辨率的Gabor特征，但只假設了高低分辨率之間存在線性關系。而在流形學習中，認為高低分辨率人臉具有相似的內在結構。相比于簡單的局部線性回歸，使用流形學習進行HR Gabor特征預測，更能準確地預測HR人臉。

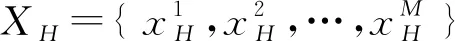
嵌入算法在高分辨率人臉重建應用中，對于輸入的低分辨率人臉特征：

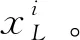
(2)

③ 通過結構權重和對應K個近鄰的高分辨率來計算高分辨率Gabor人臉特征：

(3)

1.3 典型相關分析

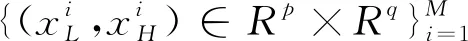
(4)

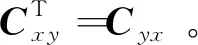
1.4 隨機CCA

雖然CCA能夠最大化2組變量之間的相關性，但是CCA是基于線性相關的，所以不能準確反映非線性關系。為了克服CCA這一缺點，一系列的非線性拓展算法相繼提出。比如Kernel CCA[15]，利用核函數來構造2組變量的非線性關系；再如Deep CCA[16]，利用DNN網絡來訓練2組變量的非線性關系；但是這些算法雖然提高了相關性，但也具有相當高的計算復雜度和時間復雜度。David[17]提出了利用隨機策略來構造可以與線性算法結合使用揭示非線性特征。其公式為：

(5)

(6)

通過拉格朗日乘法，得出Urandom和Vrandom，即為：

(7)

為了避免過擬合，添加了μ和k兩個懲罰項：

(8)

1.5 Gabor特征幻影的低分辨率人臉識別

類似于CCA，選擇前d個特征值對應的特征向量Wl=(α1，α2，…，αd)和Wh=(β1，β2，…，βd)，將Wl，Wh稱為廣義典型投影向量，并且使用式(9)和式(10)組合的特征稱為廣義規范判別特征。即：

(9)

(10)

(11)

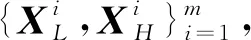
(12)

通過式(12)級聯后并使用式(13)的計分函數將其分類：

(13)

式中，G和H表示訓練集和測試集里的人臉投影到RCCA后的特征向量。

1.6 框架圖

算法框架如圖1所示，分為2個部分：訓練部分和測試部分。訓練部分：分別將高低分辨率的人臉數據集都基于Gabor進行特征提取，再通過RCCA獲取LR和HR對應的相關特征，并將其線性連接；測試部分：輸入一個LR的人臉，利用LLE構建HR的Gabor特征，分別將LR、HR映射到相關的特征中并進行線性連接；最后送入最近鄰分類器進行分類，求得識別結果。

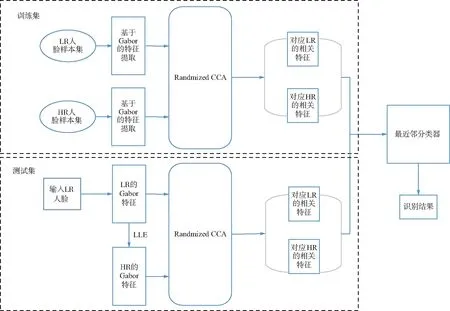
圖1 算法框架

2 實驗結果和分析

為了驗證改進算法的有效性，在YALE和ORL數據集上做了一些實驗，將LLE與LLR，GCCA與RCCA進行兩兩組合。保留PCA的97%的有效能量。實驗環境為Intel Core i7 CPU 2.2 GHz，內存8 GB，操作系統Windows 10，編程平臺為Matlab2017b。

2.1 數據集描述

YALE數據集由耶魯大學計算視覺與控制中心創建，包含15名志愿者，每名志愿者由11幅圖像組成，這些人臉包含著明顯不同的光照、表情以及姿態的變化。以YALE數據集為基礎，將48 pixel×48 pixel分辨率作為HR人臉圖像集，對該數據集依次平滑下采樣，依次獲得8 pixel×8 pixel，9 pixel×9 pixel，11 pixel×11 pixel，13 pixel×13 pixel，15 pixel×15 pixel，17 pixel×17 pixel，19 pixel×19 pixel的LR人臉數據集。

ORL數據集由劍橋大學AT&T實驗室創建，包含40名志愿者，每名志愿者由10幅圖像組成，分辨率大小統一為92 pixel×112 pixel。該數據庫人臉表情和人臉姿態有一定的變化。以ORL數據集為基礎，將48 pixel×48 pixel作為高分辨率人臉圖像集，對該數據集依次平滑下采樣，依次獲得10 pixel×10 pixel，12 pixel×12 pixel，14 pixel×14 pixel，16 pixel×16 pixel，18 pixel×18 pixel，20 pixel×20 pixel的低分辨率人臉數據集。

2.2 重建Gabor特征對比

在比對重建Gabor特征時，LR的Gabor特征分辨率為8 pixel×8 pixel，HR的Gabor特征的分辨率為48 pixel×48 pixel。如圖2和圖3所示。在YALE的人臉集中，采用峰值信噪比(PSNR)和結構相似度值(SSIM)對比LLR和LLE算法重建的Gabor特征，所考慮的尺度和方向分別為5和8。

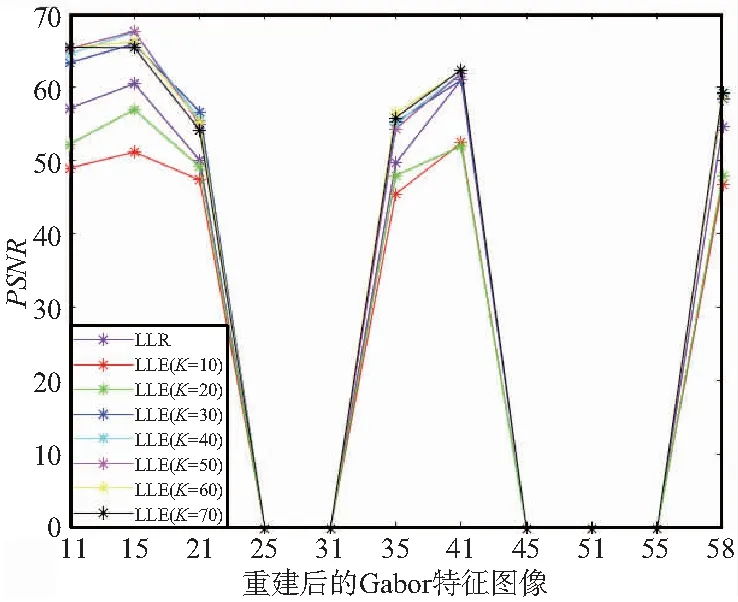
圖2 重建Gabor特征得PSNR對比

圖3 重建Gabor特征得SSIM對比

從圖2和圖3可以得出，在PNSR的比對中，LLR算法重建特征效果好于K=10和K=20的，在K為30，40，...，70時，效果均小于LLE算法的重建效果；在SSIM的比對中，LLE算法的重建效果都好于LLR算法的重建。

2.3 YALE數據集上的實驗

在YALE數據集的實驗中，每位志愿者隨機抽取5張人臉作為訓練集，其余作為測試集。將48 pixel×48 pixel作為HR人臉，LR人臉范圍9 pixel×9 pixel～19 pixel×19 pixel。在LLE算法中，K取值為30；RCCA中的懲罰項μ和κ設置為0.001。實驗結果如表1和圖4所示。

表1 YALE上不同算法在不同分辨率下的識別率

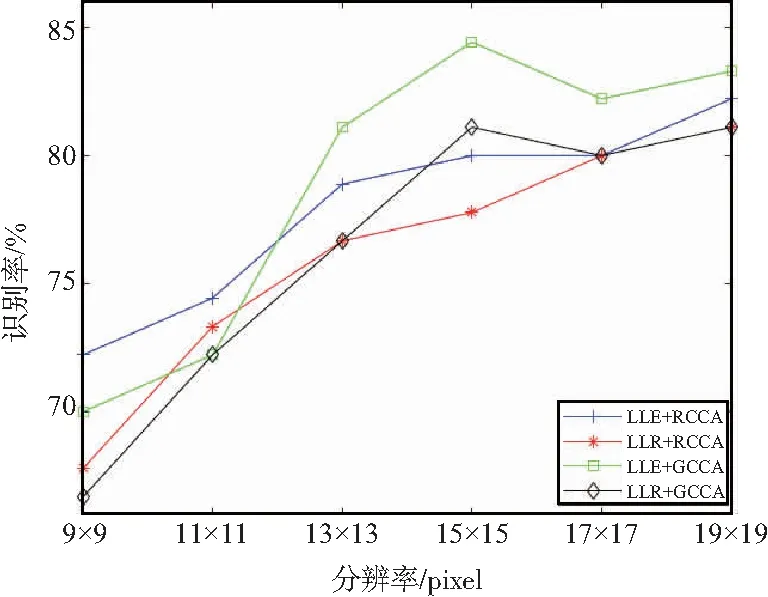
圖4 YALE上各類算法識別率

通過實驗結果比對，本文基于LLE算法而改進的重建HR人臉的Gabor特征，在不同分辨率下，識別率均高于原論文中基于LLR算法而重建的HR人臉Gabor特征；本文所提出的基于LLE重建Gabor特征，結合原論文中的GCCA算法，能夠在不同的LR下擁有最高的識別率；本文提出的LLE+RCCA的改進算法在不同分辨率下普遍高于原算法的LLR+GCCA的組合，尤其是在超低分辨率9 pixel×9 pixel時，依然有72.22%的識別率。

2.4 在ORL數據集上的實驗

在ORL人臉數據集的實驗中，每位志愿者隨機抽取5幅人臉作為訓練集，其余作為測試集，以48 pixel×48 pixel作為HR人臉，LR范圍10 pixel×10 pixel～20 pixel×20 pixel。在LLE算法中，K值選取為40；RCCA中的懲罰項μ和κ設置為0.001。實驗結果如表2和圖5所示。

表2 ORL上不同算法在不同分辨率下的識別率

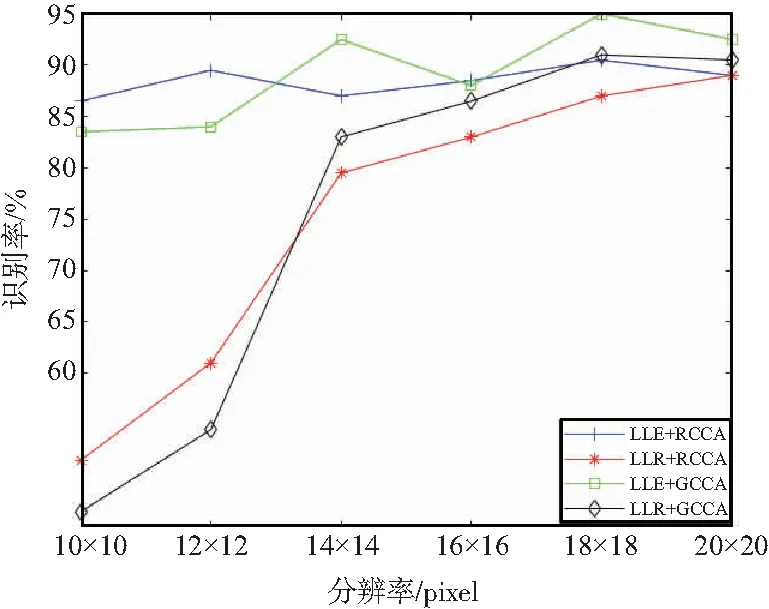
圖5 ORL上各類算法識別率

更換實驗數據集，將實驗放在ORL數據集上測試。由于ORL數據集的環境干擾比較少，所以識別率普遍提高。也得到和YALE數據集相似的結論：本文基于LLE算法而改進的重建HR人臉的Gabor特征，在不同分辨率下，識別率均高于原論文中基于LLR算法而重建的HR人臉Gabor特征；本文所提出的基于LLE重建Gabor特征，結合原論文中的GCCA算法，能夠在不同LR下擁有最高的識別率；本文提出的LLE+RCCA的改進算法在不同分辨率下普遍高于原算法的LLR+GCCA的組合，尤其是在超低分辨率10 pixel×10 pixel時，依然有86.50%的識別率；

3 結束語

本文提出了基于改進的Gabor特征幻影的人臉識別算法，在Pong的算法上提出了改進。主要有以下2點：采用基于流形學習的LLE算法取代原論文的LLR算法，更加注重高低分辨率之間的非線性關系；在特征投影方面，采用RCCA算法，更加注重訓練集的非線性特征。在上述實驗結果中，改進后的算法提高了識別率，尤其是極低分辨率的情況下。