神經(jīng)網(wǎng)絡(luò)算法加速天線優(yōu)化設(shè)計(jì)
李 闖,陳 星,程 陽
(四川大學(xué) 電子信息學(xué)院,四川 成都 610065)
0 引言
傳統(tǒng)天線設(shè)計(jì)方法通常依賴于天線設(shè)計(jì)人員的工作經(jīng)驗(yàn)和理論知識(shí),設(shè)計(jì)過程不僅復(fù)雜而且耗時(shí)長,也難以做到最優(yōu)設(shè)計(jì)。近年來,天線優(yōu)化設(shè)計(jì)得到了重視和研究。它采用天線數(shù)值計(jì)算方法對(duì)天線相關(guān)性能進(jìn)行全波數(shù)值仿真,利用遺傳算法等現(xiàn)代優(yōu)化算法實(shí)現(xiàn)對(duì)天線結(jié)構(gòu)的計(jì)算機(jī)輔助設(shè)計(jì),其基本原理是將天線設(shè)計(jì)轉(zhuǎn)化為遺傳算法的搜索尋優(yōu)過程。已有研究表明[1-2],天線優(yōu)化設(shè)計(jì)能夠節(jié)省設(shè)計(jì)者大量精力,同時(shí)擴(kuò)寬天線設(shè)計(jì)范圍,提高設(shè)計(jì)精度,成為現(xiàn)代天線研究的一個(gè)新熱點(diǎn)。但優(yōu)化設(shè)計(jì)過程中需要反復(fù)執(zhí)行天線全波數(shù)值仿真,占據(jù)了絕大部分優(yōu)化設(shè)計(jì)耗時(shí)。
神經(jīng)網(wǎng)絡(luò)算法由于可以快速進(jìn)行大量運(yùn)算,且能充分逼近任意復(fù)雜的非線性關(guān)系,因而非常適合求解像天線這種結(jié)構(gòu)參數(shù)與相關(guān)性能存在復(fù)雜的非線性關(guān)系的問題。文獻(xiàn)[3]利用3層BP神經(jīng)網(wǎng)絡(luò)模型對(duì)一個(gè)貼片天線的S11進(jìn)行了預(yù)測(cè),大大提高了天線設(shè)計(jì)效率。文獻(xiàn)[4]提出了一種基于徑向基神經(jīng)網(wǎng)絡(luò)的方法,并用于計(jì)算由共線短偶極子和并行短偶極子構(gòu)成的均勻線性陣列的方向圖,該方法同樣適用于短偶極子平面陣列的計(jì)算[5]。但它們均只是單純的將神經(jīng)網(wǎng)絡(luò)運(yùn)用于天線相關(guān)性能的預(yù)測(cè),預(yù)測(cè)完全脫離了全波數(shù)值仿真。從而可能會(huì)造成神經(jīng)網(wǎng)絡(luò)算法預(yù)測(cè)誤差對(duì)天線優(yōu)化設(shè)計(jì)的結(jié)果產(chǎn)生不良影響。
本文對(duì)神經(jīng)網(wǎng)絡(luò)算法在天線優(yōu)化設(shè)計(jì)中的應(yīng)用進(jìn)行了研究,提出了一種新的方法,通過一款雙頻偶極子天線的優(yōu)化設(shè)計(jì)對(duì)該方法的可行性進(jìn)行了驗(yàn)證。結(jié)果表明,與傳統(tǒng)遺傳算法相比,在設(shè)計(jì)的天線性能相當(dāng)情況下,該方法能夠節(jié)省設(shè)計(jì)過程中70%的全波數(shù)值仿真,后20代計(jì)算耗時(shí)減小為原來的30.6%,說明利用該方案能加快天線的優(yōu)化設(shè)計(jì)。
1 遺傳算法
遺傳算法[6-8]是模仿自然界生物進(jìn)化機(jī)制而發(fā)展起來的一種基于生物遺傳和進(jìn)化機(jī)理過程的隨機(jī)全局搜索和優(yōu)化算法。它最初由美國Michigan大學(xué)J.H.Holland教授和他的學(xué)生在1962年提出。它把自然界“優(yōu)勝劣汰,適者生存”的生物進(jìn)化原理引入優(yōu)化參數(shù)形成的編碼串群體中,按照所設(shè)定的適應(yīng)度函數(shù)并通過遺傳中的選擇、交叉和變異對(duì)個(gè)體進(jìn)行篩選,使適應(yīng)度值好的個(gè)體被保留,適應(yīng)度差的個(gè)體被淘汰,新的群體既繼承了上一代的遺傳信息,并且又優(yōu)于上一代。這樣反復(fù)循環(huán),直到滿足條件[9-11]。其程序流程圖如圖1所示。由于遺傳算法的搜索不依賴于梯度信息和能全局尋優(yōu),非常適用于天線設(shè)計(jì)這類復(fù)雜和非線性問題的求解[12]。
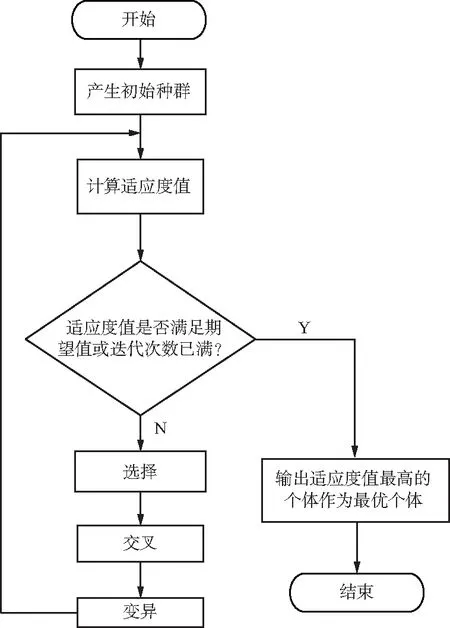
圖1 遺傳算法程序流程
2 神經(jīng)網(wǎng)絡(luò)算法
人工神經(jīng)網(wǎng)絡(luò)[13-15](Artificial Neural Network,ANN)是一種模仿生物神經(jīng)網(wǎng)絡(luò)行為特征,進(jìn)行分布式并行信息處理的算法數(shù)學(xué)模型。其早期的研究工作可以追溯到20世紀(jì)40年代,由美國兩位科學(xué)家W.Mcculloch和W.Pitts首先提出的M-P模型。它具有類似人腦一樣可以聯(lián)想存儲(chǔ)及自學(xué)習(xí)的能力。基于神經(jīng)網(wǎng)絡(luò)的優(yōu)化計(jì)算就是利用神經(jīng)網(wǎng)絡(luò)的聯(lián)想存儲(chǔ)及自學(xué)習(xí)功能,以系統(tǒng)的輸入作為網(wǎng)絡(luò)的輸入,以系統(tǒng)的輸出作為網(wǎng)絡(luò)的輸出,通過反復(fù)訓(xùn)練網(wǎng)絡(luò),最終使網(wǎng)絡(luò)預(yù)測(cè)輸出與期望輸出之間的誤差達(dá)到所設(shè)定的標(biāo)準(zhǔn)。這樣,在相同的輸入下,就可以用網(wǎng)絡(luò)的預(yù)測(cè)輸出來模擬原系統(tǒng)的輸出。由于神經(jīng)網(wǎng)絡(luò)具有非常強(qiáng)的非線性映射能力,以及可以快速進(jìn)行大量運(yùn)算,非常適合求解像天線這種結(jié)構(gòu)參數(shù)與相關(guān)性能存在復(fù)雜的非線性關(guān)系的問題[16]。
3 神經(jīng)網(wǎng)絡(luò)算法加速天線優(yōu)化設(shè)計(jì)
本文提出了一種新的方法,并通過一個(gè)雙頻偶極子天線的優(yōu)化設(shè)計(jì)對(duì)該方法進(jìn)行了技術(shù)上的實(shí)際效率和有效性論證。
3.1 設(shè)計(jì)思路
由于采用傳統(tǒng)遺傳算法進(jìn)行天線的優(yōu)化設(shè)計(jì)時(shí),遺傳算法中每個(gè)個(gè)體都對(duì)應(yīng)一個(gè)天線模型,而每一個(gè)模型都會(huì)進(jìn)行全波數(shù)值分析,這樣會(huì)耗費(fèi)大量的計(jì)算時(shí)間。而單純地將神經(jīng)網(wǎng)絡(luò)算法用來對(duì)天線相關(guān)性能進(jìn)行預(yù)測(cè),其預(yù)測(cè)精度往往與網(wǎng)絡(luò)模型的選擇存在密切關(guān)系,且神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)的選擇目前尚無一種統(tǒng)一而完整的理論指導(dǎo),一般只能由經(jīng)驗(yàn)選定,這樣可能會(huì)造成由于所選取的網(wǎng)絡(luò)模型預(yù)測(cè)誤差較大。而用遺傳算法作優(yōu)化是通過選擇、交叉和變異操作的迭代獲得更高適應(yīng)度值設(shè)計(jì)結(jié)果,適應(yīng)度值計(jì)算結(jié)果誤差可能導(dǎo)致錯(cuò)誤的優(yōu)化方向和結(jié)果,從而得不到滿足基本要求的結(jié)果。
本文將神經(jīng)網(wǎng)絡(luò)算法運(yùn)用于天線的優(yōu)化設(shè)計(jì),提出了一種新的設(shè)計(jì)思路:在遺傳算法優(yōu)化設(shè)計(jì)天線初期仍采用全波數(shù)值仿真,為神經(jīng)網(wǎng)絡(luò)算法提供訓(xùn)練樣本;由于遺傳算法優(yōu)化設(shè)計(jì)天線方向和結(jié)果主要由少量的高適應(yīng)度值個(gè)體決定,在神經(jīng)網(wǎng)絡(luò)算法預(yù)測(cè)代替全波數(shù)值仿真后,對(duì)高適度值個(gè)體采用全波數(shù)值仿真進(jìn)行驗(yàn)證,不僅保證優(yōu)化設(shè)計(jì)的正確性,同時(shí)更新神經(jīng)網(wǎng)絡(luò)算法訓(xùn)練樣本庫,提高預(yù)測(cè)準(zhǔn)確度。該方法設(shè)計(jì)流程如圖2所示。

圖2 神經(jīng)網(wǎng)絡(luò)算法加速天線優(yōu)化設(shè)計(jì)流程
3.2 雙頻偶極子天線優(yōu)化設(shè)計(jì)
本文通過一款工作于2.45 GHz和5.8 GHz的雙頻偶極子天線的優(yōu)化設(shè)計(jì),驗(yàn)證上述方案的可行性。天線結(jié)構(gòu)如圖3所示。
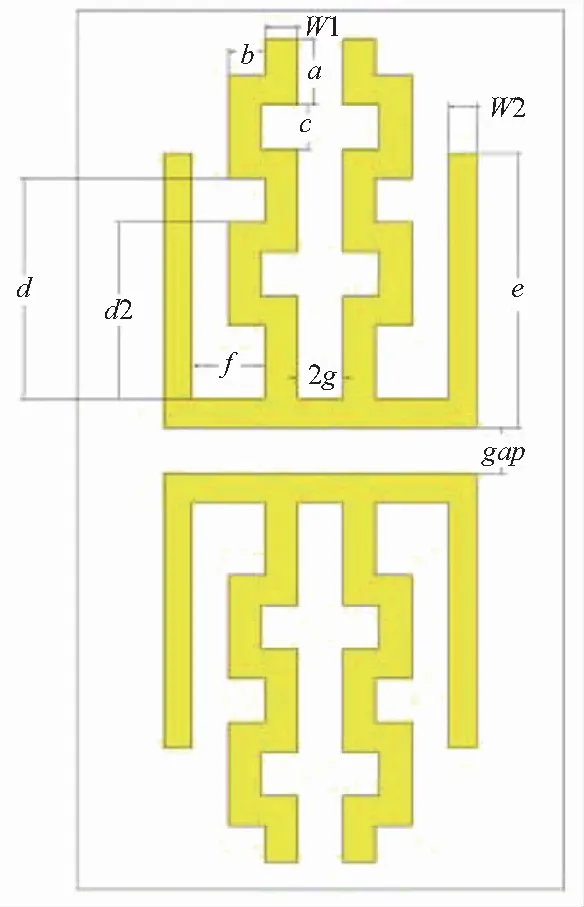
圖3 雙頻偶極子天線結(jié)構(gòu)
其中部分參數(shù)所代表的含義如表1所示。

表1 部分參數(shù)的含義
對(duì)于該天線,需滿足如下基本要求:① 帶寬:2 400~2 500 MHz(4.1%)&5 000~6 000 MHz(18%),且天線帶寬盡可能寬;② 水平面增益盡可能高,不圓度盡可能小(即水平全向);③ 垂直極化多一些。
該天線所用的介質(zhì)板為長40 mm,寬20 mm的FR4板材,考慮到該板材的尺寸,需對(duì)天線進(jìn)行小型化處理,因此本文對(duì)振子進(jìn)行了彎折以確保其尺寸在規(guī)定范圍內(nèi)。
3.3 遺傳算法參數(shù)設(shè)置與神經(jīng)網(wǎng)絡(luò)模型建立
在本文中,所設(shè)置的種群規(guī)模為60代,其中每一代20個(gè)個(gè)體。前40代用全波仿真軟件進(jìn)行分析,將得到的數(shù)據(jù)作為訓(xùn)練樣本,訓(xùn)練已經(jīng)建立好的神經(jīng)網(wǎng)絡(luò)。由于前面40代中,適應(yīng)度值不小于0.5的個(gè)體大約占總個(gè)體的30%,所以本文對(duì)于后20代中每一代只用全波仿真軟件計(jì)算其中的30%的個(gè)體,其余個(gè)體的適應(yīng)度值用神經(jīng)網(wǎng)絡(luò)去預(yù)測(cè)。待優(yōu)化的變量及其相應(yīng)的優(yōu)化范圍、編碼長度如表2所示。所設(shè)定的適應(yīng)度函數(shù)為:
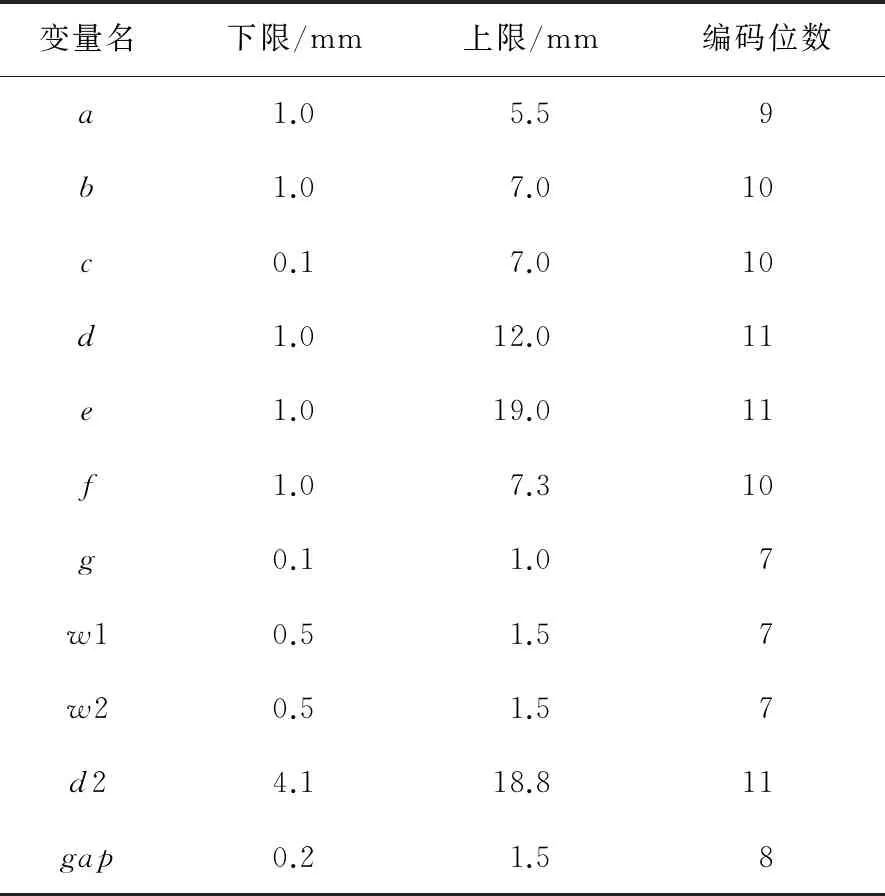
表2 待優(yōu)化變量及其相應(yīng)的優(yōu)化范圍、編碼長度
fitness=(BW1+BW2)×k1+(Gain1+Gain2)×
k2-(Φ1+Φ2)×k3,
式中,BW1,BW2分別為2.45,5.5 GHz處的帶寬;Gain1,Gain2分別為2.45,5.5 GHz處的增益;Φ1,Φ2分別為2.45,5.5 GHz處的不圓度;k1,k2,k3為權(quán)重因子,本文中取k1,k2,k3的值分別為0.5,0.2,0.3。
神經(jīng)網(wǎng)絡(luò)模型采用雙隱含層的多層感知器結(jié)構(gòu),學(xué)習(xí)算法為BP(Back Propagation)學(xué)習(xí)算法。其中第一個(gè)隱含層有25個(gè)神經(jīng)元,第二個(gè)隱含層有24個(gè)神經(jīng)元。輸入樣本為待優(yōu)化的11個(gè)變量,輸出為對(duì)應(yīng)個(gè)體的適應(yīng)度值。
4 兩種方案結(jié)果對(duì)比
在本文中,首先將采用傳統(tǒng)遺傳算法與基于本文方法2種方案對(duì)該天線進(jìn)行優(yōu)化設(shè)計(jì)作了天線相關(guān)性能上的對(duì)比,以驗(yàn)證本文所提出的方案的有效性,然后在此基礎(chǔ)上對(duì)本方案的計(jì)算耗時(shí)及設(shè)計(jì)準(zhǔn)確度進(jìn)行了分析。
4.1 天線性能對(duì)比
圖4~圖6為上述2種方案所得的天線相關(guān)性能曲線。
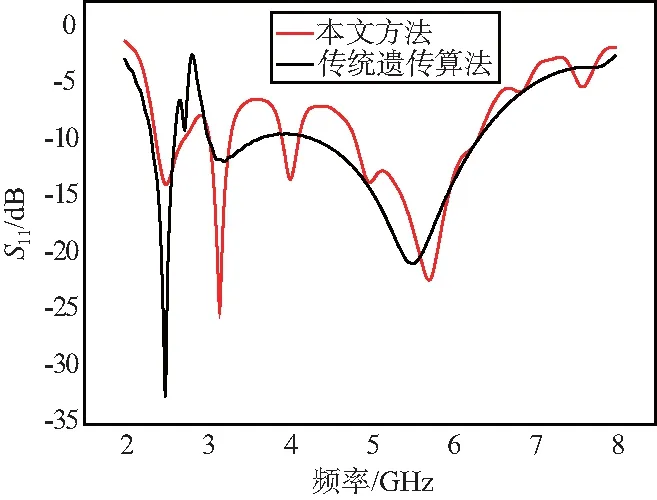
圖4 兩種方案S11曲線對(duì)比

圖5 兩種方案在2.45 GHz處的 H面方向圖對(duì)比

圖6 兩種方案在5.5 GHz處的 H面方向圖對(duì)比
通過圖4可看出,基于傳統(tǒng)遺傳算法優(yōu)化出的天線的S11≤ -10 dB的阻抗帶寬為2.32~2.6 GHz(11.4%)&4.4~6.28 GHz(34.2%)。
相比較之下,采用本文所提出的方法優(yōu)化出的天線的S11≤ -10 dB的阻抗帶寬為2.39~2.69 GHz(12.2%)&4.83~6.29 GHz(26.5%)。
由圖5可以看出,基于傳統(tǒng)遺傳算法優(yōu)化出的天線在2.45 GHz處的增益為1.93 dBi,不圓度為0.05 dB。采用本文所提出的方法優(yōu)化出的天線在2.45 GHz處的增益為2.46 dBi,不圓度為0.27 dB。
由圖6可以看出,基于傳統(tǒng)遺傳算法優(yōu)化出的天線在5.5 GHz處的增益為3.56 dBi,不圓度為1.4 dB。采用本文所提出的方法優(yōu)化出的天線在5.5 GHz處的增益為1.97 dBi,不圓度為1.82 dB。
通過上述對(duì)比可以看出,與傳統(tǒng)遺傳算法相比,利用本文方法對(duì)該天線進(jìn)行優(yōu)化,所得到的天線性能相當(dāng)。
4.2 天線設(shè)計(jì)耗時(shí)與預(yù)測(cè)準(zhǔn)確度分析
圖7和圖8分別為上述2種方案在計(jì)算耗時(shí)上的對(duì)比,以及將本文方法用于該天線優(yōu)化設(shè)計(jì)中后面20代中每代30%的個(gè)體預(yù)測(cè)適應(yīng)度值與傳統(tǒng)遺傳算法得出的適應(yīng)度值的誤差曲線。
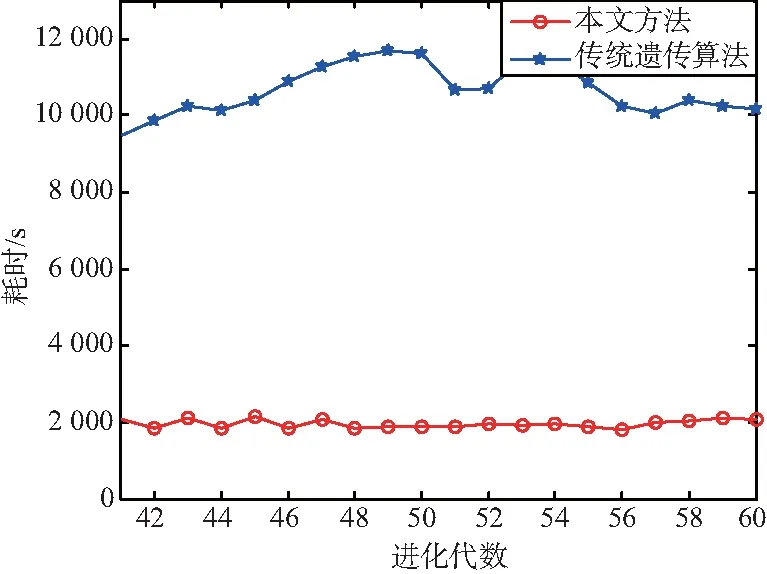
圖7 兩種方案剩余20代計(jì)算耗時(shí)對(duì)比
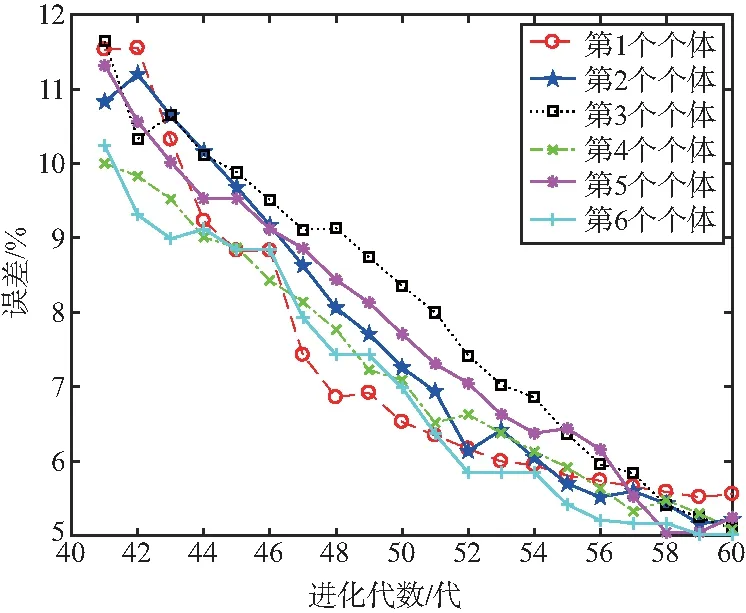
圖8 剩余20代中每代適應(yīng)度值最大的6個(gè)個(gè)體誤差曲線
由圖7可以看出,與傳統(tǒng)遺傳算法相比,本文方法在后面的20代中只需對(duì)每代30%的個(gè)體進(jìn)行全波分析。且與傳統(tǒng)遺傳算法對(duì)20代每的個(gè)體進(jìn)行全波分析所需的38.9 h相比,該方法耗時(shí)僅需11.9 h,計(jì)算耗時(shí)減小為原來的30.6%。
由圖8可以看出,本文所建立的神經(jīng)網(wǎng)絡(luò)模型對(duì)天線適應(yīng)度值的預(yù)測(cè)結(jié)果與傳統(tǒng)遺傳算法優(yōu)化結(jié)果之間的初始誤差為11.53%,隨著進(jìn)化代數(shù)的增加,誤差逐漸減小,最后誤差降為5.02%。通過分析可知,本文提出將適應(yīng)度值較大的30%個(gè)個(gè)體用全波數(shù)值分析加以驗(yàn)證,能夠保證在用遺傳算法優(yōu)化過程中不會(huì)因?yàn)樯窠?jīng)網(wǎng)絡(luò)本身的預(yù)測(cè)誤差而受到影響,使適應(yīng)度值較大的個(gè)體被保留,從而讓迭代過程一步步逼近最優(yōu)解。且后續(xù)更新訓(xùn)練樣本庫,能夠保證由于訓(xùn)練樣本數(shù)的增加,神經(jīng)網(wǎng)絡(luò)本身的預(yù)測(cè)能力會(huì)增加,從而使神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)結(jié)果與傳統(tǒng)遺傳算法優(yōu)化結(jié)果之間的誤差逐漸減小。
5 結(jié)束語
天線優(yōu)化設(shè)計(jì)能夠減少天線設(shè)計(jì)的人工勞動(dòng)和縮短設(shè)計(jì)時(shí)間,結(jié)合神經(jīng)網(wǎng)絡(luò)等人工智能算法能夠大幅度地提高天線優(yōu)化設(shè)計(jì)效率,有重要的理論價(jià)值和工程應(yīng)用前景。本文對(duì)于神經(jīng)網(wǎng)絡(luò)算法加速天線優(yōu)化設(shè)計(jì)進(jìn)行了研究,提出了一種新方法,并通過一款微帶雙頻偶極子天線的優(yōu)化設(shè)計(jì)對(duì)該方法進(jìn)行了驗(yàn)證。結(jié)果表明,本文方法與傳統(tǒng)遺傳算法優(yōu)化設(shè)計(jì)相比,在設(shè)計(jì)天線性能相當(dāng)?shù)那闆r下,能夠節(jié)省設(shè)計(jì)過程中70%的全波數(shù)值仿真,后20代計(jì)算耗時(shí)縮短為原來的30.6%。證明將該方法應(yīng)用于加速天線優(yōu)化設(shè)計(jì)中具有可行性。

