標準累積絕對速度CAVSTD 在高鐵地震預警中的可行性分析

崔恩文

（連云港職業技術學院 建筑工程學院，江蘇 連云港222006）

1 標準累積絕對速度CAVSTD 簡介

美國電力研究所（EPRI）最早提出累積絕對速度CAV 的概念，并用于作為核電廠預警參數[1]。為了提高核電預警的準確性，隨后引入標準累積絕對速度CAVSTD的概念，規定為用時間間隔為1 秒將加速度時程進行N 等分，找出N 等分中加速度超過0.025g 的等分并對其進行積分，之后對整個時程進行累加求和，具體表達式如（1）所示：

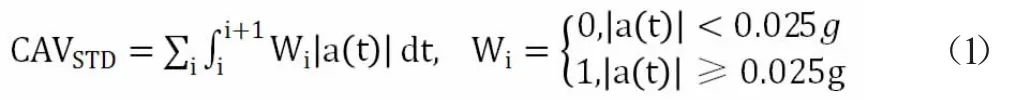
2 標準累積絕對速度CAVSTD 在高鐵地震預警中的應用

鑒于標準累積絕對速度CAVSTD在核電預警中的優越性，黃俊等依托汶川地震數據，分析CAVSTD在高鐵預警中的可行性，研究發現CAVSTD參數在高鐵地震監測預警中可以有效的排除破壞性小的高頻小震，但對破壞性小的遠震大震可能會產生誤報現象，為此必須聯合峰值加速度PGA 進行報警，這樣可以有效的排除近震小震及遠震大震對高鐵地震報警的干擾[2]，但此時僅僅是基于起算閾值為0.025g 的累積絕對速度CAVSTD，為此有必要探討基于相關起算閾值的累積絕對速度CAV 在高鐵地震預警中的應用。

3 高鐵地震預警參數CAV 起算閾值初探

3.1 模型介紹[3-6]

以SY97477 高速列車為例，該列車主要由一個車體、兩個轉向架及四個輪對組成的多自由度系統，各部分均由一二系彈簧和阻尼銜接，具體結構可見圖1。

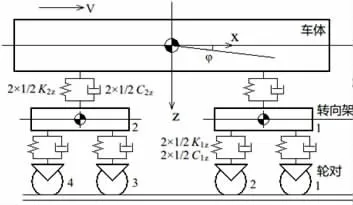
圖1 列車模型

列車模型不同組成部分的幾何尺寸、質量、轉動慣量、剛度及阻尼等，其具體物理意義可參考文獻[4-6]。

為簡化模型并考慮計算精度的要求，假設結構體系各部分均為剛體并作小幅度振動，各銜接系統均為線性，列車勻速運行。以車體重心為坐標原點建立相互獨立的空間坐標系，分別用X、Y、Z 坐標軸來確定列車模型的空間位置，其中列車沿X 軸方向運行，具體如圖2 所示。

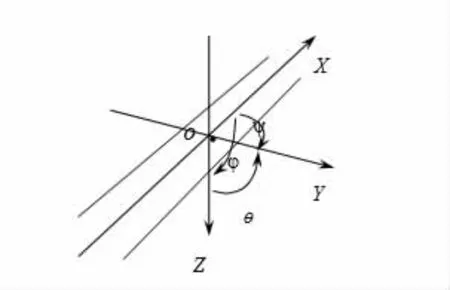
圖2 車體在空間的坐標位置

基于上述假設列車的自由度數如表1 所示，表2 顯示車體和轉向架分別有5 個獨立的自由度，輪對有4 個獨立的自由度，故此列車模型系統共有31 個自由度。

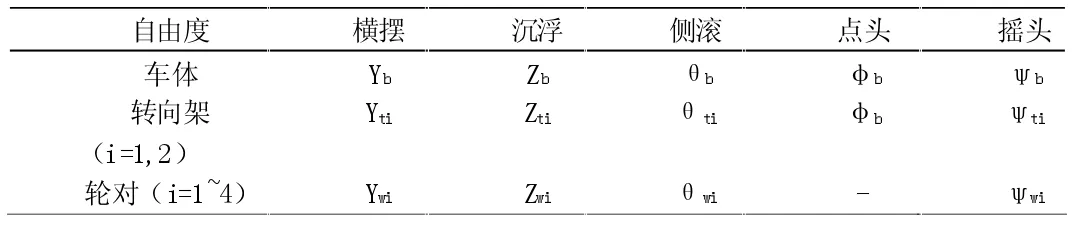
表1 列車自由度數確定[4-6]

3.2 方程建立及求解方法

基于以上數據將模型各部分運動表達式列為矩陣，如式（2）所示。

式中，{U''}、{U'}、{U}分別為車輛沿不同自由度的廣義加速度矢量、廣義速度矢量和廣義位移矢量；{p}為廣義荷載矢量，本文主要包含輪軌力和地震力，其中輪軌力可依據Hertz 非線性接觸理論、Kalker 線性理論及Hedrick-Elkinss 理論進行求解[4-6]，該方程可運用Newmark-β 法求解列車動態響應[4-6]。

3.3 CAV 起算閾值確定

通過Matlab 軟件對上述列車模型進行編程，引入德國軌道不平順與簡諧波(只考慮Y 方向輸入) 分別作為內部與外部激勵，依據鐵道部給出評判列車安全運行指標，考慮動力放大系數2.55[3-6]，計算給出不同車速下簡諧波臨界幅值與頻率的變化關系，如圖3 所示，其中評判列車安全運行指標如表2 所示，德國軌道不平順見參考文獻[4]。

表2 列車安全運行評判指標[4]

圖3 不同車速對應的影響列車安全運行臨界狀態下的簡諧波臨界幅值與周期的變化關系

從圖3 可知，當車速不變時，幅值小于0.025g 的中低頻簡諧波也可能導致列車發生脫軌事故，若不考慮低于0.025g 的簡諧波對列車安全運行的影響，此時基于起算閾值為0.025g 的標準累積絕對速度CAVSTD在高鐵地震預警應用中過于保守，為此需要考慮基于相關起算閾值的累積絕對速度CAV 作為高鐵地震預警參數。從圖3 可以發現，簡諧波臨界幅值隨著周期變長逐漸減小并趨于定值，從而可以忽略幅值低于該定值的任何簡諧波對列車運行安全的影響，此時不同車速下對應的定值即為CAV 的起算閾值，如表3 所示。

表3 不同車速下CAV 的起算閾值

由表3 知，車速200Km/h 時，CAV 的起算閾值為0.008g；車速在250km/h 及以上時，CAV 的起算閾值相同，均為0.004g。

4 結論

通過分析車輛在軌道不平順及簡諧波共同作用下的動態響應，依據相關規范給出影響列車安全運行臨界狀態下簡諧波幅值與周期的關系，發現不同車速下簡諧波幅值隨著周期變長逐漸遞減最終趨于定值，可以忽略幅值低于該定值的簡諧波對列車安全運行的影響，從而得出不同車速下CAV 的起算閾值，由此可知基于起算閾值0.025g 的標準累積絕對速度CAVSTD作為高鐵地震預警參數過于保守，應當考慮不同車速下基于相關起算閾值的累積絕對速度CAV 作為高鐵地震預警參數。