甚高頻無線通信頻偏估計算法研究

艾雨

（民航西南空管局技術(shù)保障中心，四川 成都610043）

隨著民航業(yè)的快速發(fā)展，對民航地空通信的通信質(zhì)量的要求也越來越高，由于多普勒效應(yīng)的存在使得頻偏的產(chǎn)生是一個無法避免的現(xiàn)象，但是通過有效的頻偏估計算法能準確的預(yù)估頻偏值，最終大大的減小頻偏對接收機性能的影響，從而提高地空甚高頻通信的質(zhì)量。目前常用的無線通信頻偏估計算法有StevenA.Tretter 提出的線性回歸算法，即StevenA.Trette 頻偏估計算法，而Kay 在1989 年又對Steven A.Tretter 提出的算法進行了改進，該改進算法是一種基于差分相角模型的估計算法。近年，隨著數(shù)字信號處理系統(tǒng)的發(fā)展，基于數(shù)字信號處理的FFT載波頻偏估計算法、PMF-FFT 算法則更多的運用到工程實踐中, 文章重點對比了Kay 算法、FFT 算法、PMF-FFT 算法三種算法的優(yōu)劣，找出更適合在民航VHF 通信系統(tǒng)中使用的頻偏估計算法，進一步提高甚高頻接收機的性能。

1 頻偏原理概述

在高頻、甚高頻通信系統(tǒng)中，往往因為系統(tǒng)發(fā)信機/收信機本振振蕩器的精確度通常( ＜-6PPM)以及頻率的多普勒效應(yīng)等原因，使得接收信號的頻率與接收機本振頻率無法完全相同，兩者會產(chǎn)生差值，即頻偏。頻偏將嚴重影響接收機的工作性能，降低接收效果。接收機在解調(diào)的下變頻的過程中，要產(chǎn)生一個與接收信號同頻同相的本地載波，但頻偏的存在，使接收機難以產(chǎn)生一個與已調(diào)信號載波頻率完全一致的本地載波頻率。我們以二進制相移鍵控信號(BPSK)為例，假已調(diào)制信號為A cos 2πfωt ，而接收機產(chǎn)生 cos （ fω±f0）t 的本振信號與之相乘實現(xiàn)相干解調(diào)，則：

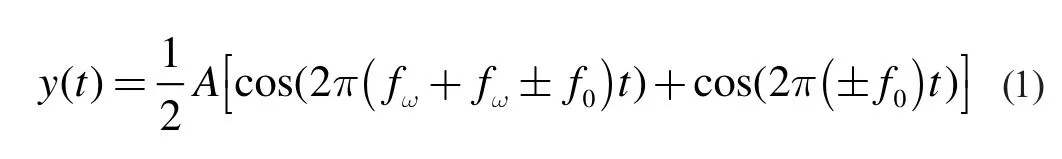
經(jīng)過低通濾波后得到：

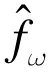
2 頻偏估計的原理

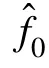
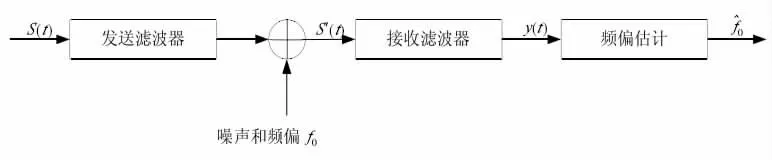
圖1 頻偏估計基本原理示意圖

在加性高斯白噪聲(Additive White Gaussian Noise)信道中，甚高頻接收機器經(jīng)濾波器后輸出信號可以表示為：

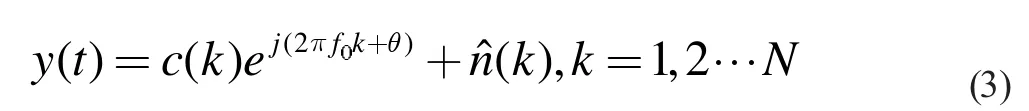
上式中，c(k)表示調(diào)制信號。N 代表頻偏估計中接收信號數(shù)據(jù)的位數(shù)，f0表示載波產(chǎn)生頻偏值，而 θ(0,2 π)則代表載波的初始相位值。

常用的頻偏估計算法可分為兩大類，第一類是基于數(shù)據(jù)的頻偏估計算法，在此類算法中調(diào)制信號是確定的；而另一類則是基于非數(shù)據(jù)的頻偏估計算法，也稱為盲估計。而在各類盲估計算法中由于已調(diào)制信號c(k)未知，因此，需要先假設(shè)c(k)的估計方法。工程中往往利用已知導(dǎo)頻符號的共軛消除對已調(diào)信號的影響，即

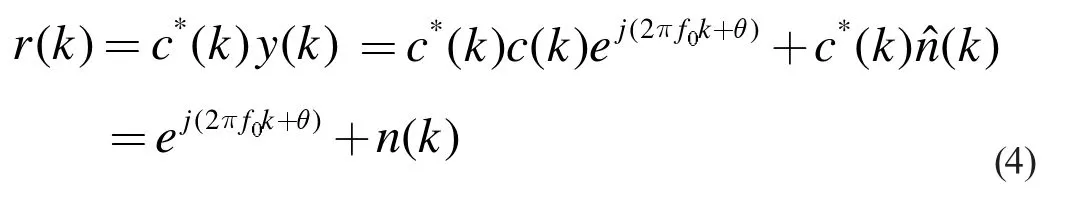
3 幾種典型的頻偏估計方法

3.1 Kay 算法

1989 年Kay 利用差分相角的數(shù)學(xué)模型提出該算法。根據(jù)文獻[2]，公式(6)的相位表示為：

其中，arg(g)表示求相角。對(5)求差分得到：

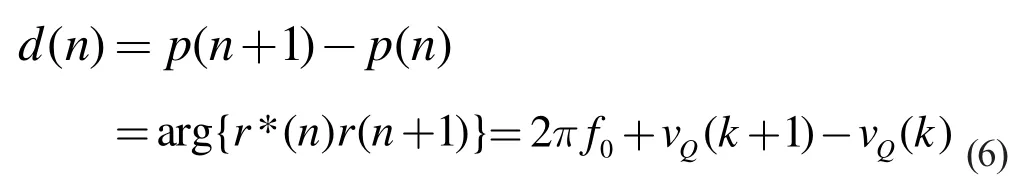
在式(6)中對參數(shù)f0的估計運算實際就是一個求有色高斯過程的平均，對參數(shù)f0作最大似然估計運算，從而得到：

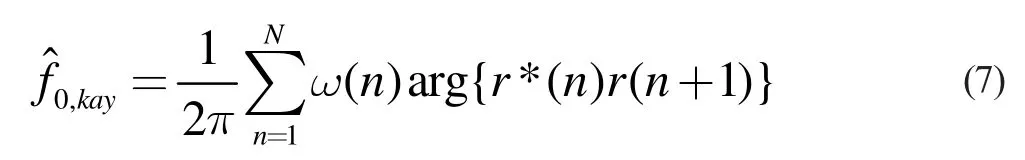
3.2 基于快速傅里葉變換(FFT)的載波頻偏算法

快速傅里葉變換有著運算速度快，信噪比門限低的性能特點。使用FFT 技術(shù)進行頻偏估計的算法原理如下圖所示。

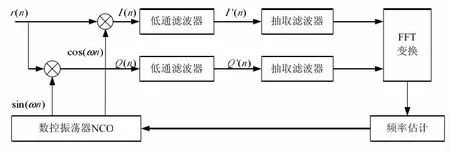
圖2 FFT 頻偏估計算法原理圖

假設(shè)在0:T 時間內(nèi)接收到的采樣信號為：

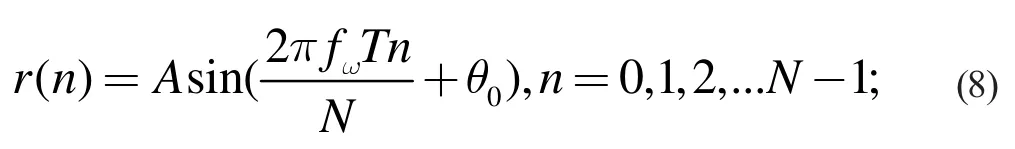
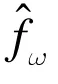
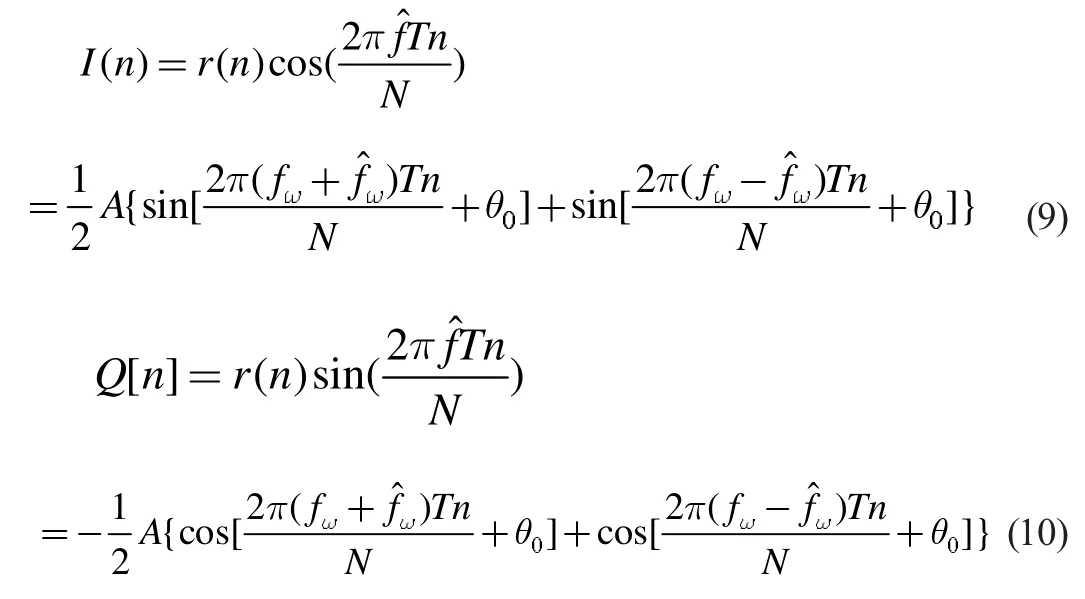
混頻后I,Q 兩路信號通過低通濾波器濾除高頻分量后得到：

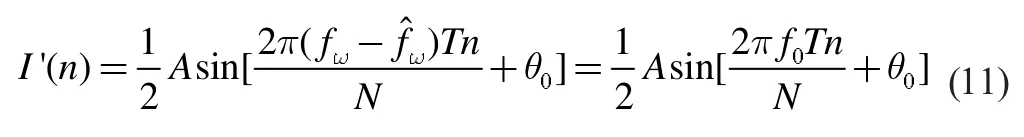
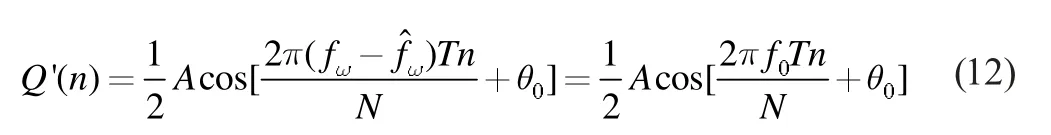
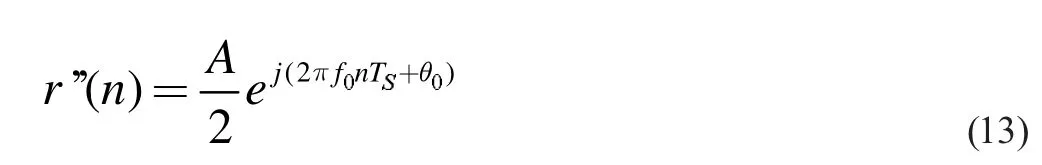
其中，Ts為經(jīng)抽取后的碼元寬度。對式13 中的序列r ’( n)補零后再進行FFT 的變換式為：

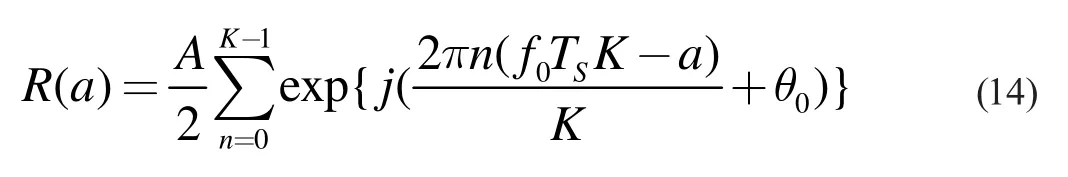
對上式再進行頻譜分析，求R(a)模值的最大點：

R ={ R (0), R( 1),..., R ( K-1)}是K 點作快速傅立葉變換后的輸出值。其最大值是 R ( amax)，則得到的頻偏估計為：

其中系統(tǒng)采樣頻率為：FS=1/TS。同時，由于快速傅里葉變換的柵欄效應(yīng)，故頻譜分辨率=采樣頻率/FFT 運算的點數(shù)K 值，即 FS/K。

3.3 基于PMF-FFT 的頻偏估計算法

由FFT 算法的原理可知，頻偏估計算法的估計精度為FS/K。因此，當采樣頻率Fs不變時，增加FFT 運算的運算點數(shù)K，可以提高估計的計算精度值。可以看出FFT 算法是以增加運算點數(shù)來獲得更高的運算精度的。而工程中往往需要一種更加折中的估計算法，而PMF-FFT 的頻偏估計算法就是一種可以在不提高運算點數(shù)的情況下提高估計精度頻偏估計的算法。

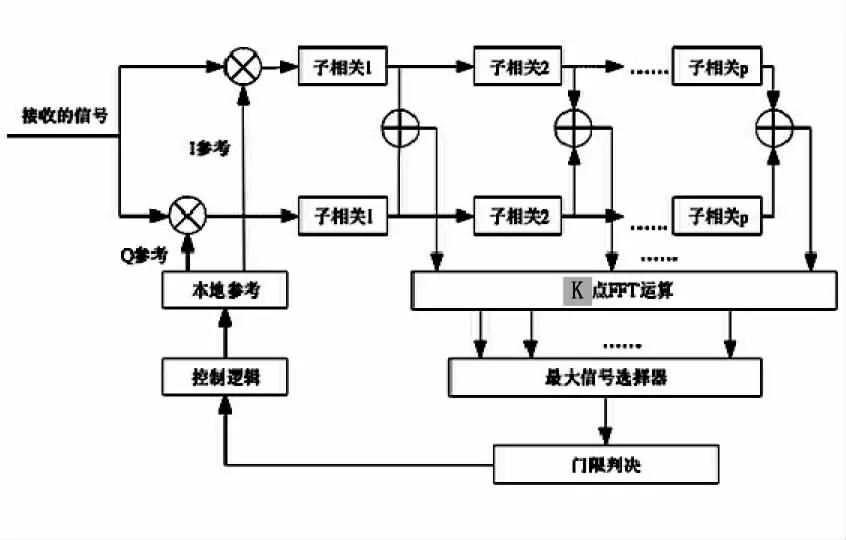
圖3 PMF-FFT 頻偏估計算法原理圖

如上圖所示，本地產(chǎn)生的偽碼與接收信號作相關(guān)運算，運算結(jié)果再進行FFT 處理。相關(guān)器由P 個分段構(gòu)成，各段的相關(guān)時間為T/P。各單元對連續(xù)X 個碼元做相關(guān)運算(X=M/P,N 為PN

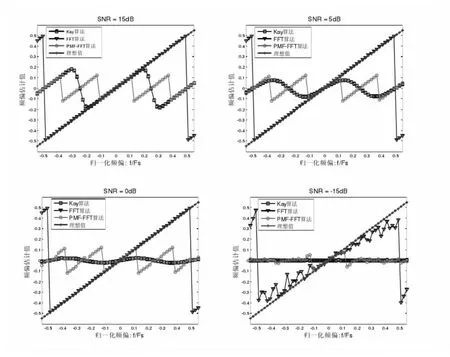
圖4 三種頻偏估計算法在不同SNR 下的性能比較

4 仿真結(jié)果分析

MATLAB 實驗?zāi)Ｐ筒捎肂PSK 調(diào)制方式，假設(shè)碼元速率為Rb=64K，PN 序列長度為N=512。FFT 的頻偏估計運算點數(shù)為512；而在PMF-FFT 頻偏估計運算中，快速傅立葉運算相關(guān)器個數(shù)設(shè)為P=128，而子相關(guān)器長度為 X = N / P=4，點數(shù)K 為128。仿真圖中可以得出，在小信噪比的信道狀態(tài)下，Kay算法的估計性能較差，離理想值偏差較大，而PMF-FFT 算法和FFT 估計算法性能穩(wěn)定，可以比較準確的估計出系統(tǒng)的頻偏，較理想頻偏值誤差較小；而隨著信噪比SNR 逐漸增大的情況下，Kay 算法的性能逐漸提升，尤其在SNR=5dB 及SNR=15dB 的仿真圖中，三種估計算法都能準確的估計出頻偏。從算法適用的估計范圍來看，F(xiàn)FT 算法的估計范圍比PMF-FFT 算法及Kay 算法更大。從計算精度來看，F(xiàn)FT 算法的精度需要與計算點數(shù)K成正比。但是，PMF-FFT 算法可以在PN 序列長度及FFT 運算點數(shù)一定的情況下進行精度的調(diào)整，其精度較FFT 算法更高。

5 結(jié)論

由上述仿真結(jié)果分析得出，在大信噪比情況下三種算法性能相近，都能較準確的估計出系統(tǒng)頻偏值。但隨著信號質(zhì)量下降，信噪比SNR 降低，Kay 算法的估計性能大幅下降，而FFT 估計算法和PMF-FFT 算法性能穩(wěn)定。從頻偏估計的適用范圍來看，Kay 算法和PMF-FFT 算法估計范圍有限，頻偏估計范圍大致為(-0.2,+0.2)以內(nèi)。而FFT 算法適用的估計范圍更廣(-0.5,+0.5)，為三種算法中最優(yōu)。計算精度方面，F(xiàn)FT 算法與PMF-FFT 算法都有著不錯的計算精度，但是在序列長度及FFT 點數(shù)有限的情況下，PMF-FFT 算法可以通過調(diào)整分段相關(guān)器長度來改變頻偏估計的精度，進而提高接收機的接收性能，綜上在較小的頻偏估計范圍內(nèi)PMF-FFT 算法更適用且效率更高。