一種基于銅柱測量的膛內燃氣最大壓力計算方法

劉 濤,張領科

(南京理工大學 能源與動力工程學院,江蘇 南京 210094)

常規的內彈道過程中,彈丸在火藥燃氣的壓力推動下加速運動,完成發射過程。因此火藥在膛內燃燒生成的燃氣壓力的變化和分布規律是內彈道學研究中的最重要參量。對膛內燃氣壓力的測量一直是實驗內彈道學的重點研究對象。在內彈道實驗中,通常采用電測壓法和塑性測壓法2種測壓方法。其中塑性測壓法以銅柱測壓法為代表,亦是目前最為常用的測壓方法。

使用銅柱測壓法測量膛壓,即利用膛內燃氣壓力使銅柱壓縮,通過銅柱壓縮量與壓力表對比得到待測膛壓的峰值。這種方法使用方便,操作簡單,經濟性好且有相當的可靠度。但由于銅柱使用靜態壓力標定而待測的火藥燃氣壓力為動態加載,使得銅柱測壓法總是存在一定的動、靜差,即由于靜態標定、動態測量所產生的誤差。一般來說,銅柱壓力與真實膛壓峰值有20%左右的差值。常用的修正方法有:①經驗修正法,②準動態標定法,③系統構建法,④預壓實驗法。

本文基于銅柱塑性狀態的動態本構關系,以預壓過程作為靜態加載參考,考慮活塞慣性力的作用,建立銅柱測壓器系統的數學模型,為動態誤差分析建立包括預壓過程在內的更為實用且簡化的數學模型。

1 減少銅柱測量誤差的基本原理

實踐證明,測壓器活塞慣性和銅柱動態本構關系是造成銅柱測壓器動、靜差的2個主要原因[1]:①火藥燃氣壓力通過測壓器活塞壓縮測壓銅柱的同時,活塞隨著火藥燃氣向銅柱壓縮方向運動,卸載時活塞由于慣性要繼續運動壓縮銅柱產生靜差,使得壓力測量值大于真實值;②塑性材料存在應變率效應,塑性材料的實際應力-應變關系與應變率有關,隨著加載速度增大,應變率增大,材料的屈服極限將提高,使壓力測量值小于真實值。在內彈道膛壓測量實驗中,材料動態本構關系的影響更大,尤其是小口徑槍炮膛內動態加載速率很大,銅柱測壓法測得的壓力小于真實壓力。本文將以銅柱應力-應變關系為基礎,對實驗中的數據處理方法進行改進簡化。

在進行銅柱測壓實驗前需要對銅柱進行預壓。不同批次銅柱之間,及同一批銅柱的個體之間,也存在著一定的機械性能的差異,為了對這一誤差進行修正,常對出廠的銅柱使用壓力機以一定壓力進行一次預壓,并記錄預壓的壓力和變形量,在測量膛內壓力時,根據預壓時體現的銅柱“軟硬程度”與同一批編表銅柱具有的平均機械性能的差異進行修正。本文通過構建銅柱的應力-應變關系,利用電子測壓器測得的壓力脈寬,提出一種通過數值計算獲得膛壓的數據處理方法,對銅柱測壓結果進行修正,并借助量綱分析及相似理論進行分析,給出了某實驗條件下的修正公式。該方法可以提高銅柱測壓精度,更接近電子測壓器,滿足靶場校驗時的更高精度的測量需求。

2 預壓過程中銅柱的本構關系

測壓銅柱常利用銅柱壓力機以緩慢加壓的方式對銅柱進行預壓。銅柱壓力機原理[2]如圖1所示。

圖1 銅柱壓力機原理

在壓力機杠桿左端有一支撐點O,右端有載荷FQ加于加載點B處,測壓銅柱放在著力點A處的升降臺上。沒有載荷時,A點的支撐彈簧恰好能維持杠桿水平平衡。預壓時在B點加上載荷FQ,并驅動升降臺緩慢上升,保持杠桿水平平衡,這時銅柱就在壓縮力F作用下發生塑性變形,由原始高度H0縮短為預壓后高度Hb,0,如圖2所示。

圖2 銅柱受力示意圖

由杠桿平衡條件可知:

(1)

在預壓過程中,由于加載過程較為緩慢,整個過程可以視為準靜態過程,可以使用靜態標定實驗得到銅柱的靜態本構關系:

(2)

式中:應力σ=F/Sc,Sc為銅柱橫截面積;ε為應變;E為彈性模量;Es為塑性段的彈性模量;σs為彈性極限。

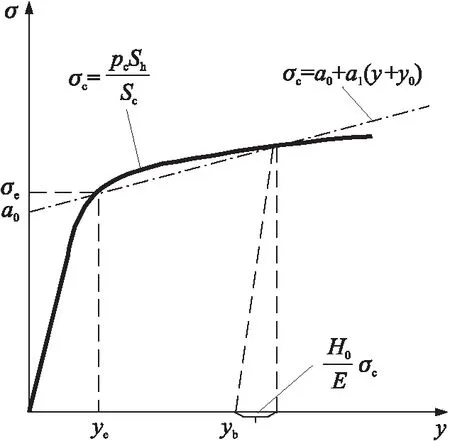
圖3 銅柱靜態加載曲線

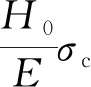
(3)

根據靜態壓力與壓后高關系表,即可通過式(3)換算σc與y的關系,該關系通常為三次多項式的形式。根據銅柱壓力對照表及實驗中的使用情況,在使用銅柱測壓法測量膛壓時,選取適當規格的銅柱的情況下,銅柱變形量與最大膛壓具有良好的線性關系[3];同時,用于測壓的銅柱在靜態壓力下的力學性能具有一定的一致性,故銅柱的靜態應力-應變關系如下:

(4)

式中:y0為預壓變形量,對于無預壓銅柱y0=0。

測壓銅柱由純凈的電解銅加工而成,含銅量不小于99.97%,軟、硬機械性能及產生的變形能均勻一致,純銅的靜態彈性極限約為30 MPa,即銅柱的彈性極限σe與應變εe為定值。通過銅柱預壓的變形量和預壓壓力即可根據式(4)得到銅柱塑性階段的彈性模量Es及式(4)中的系數a0,a1。

3 銅柱測壓系統的數學建模

3.1 基本假設

根據銅柱測壓器的工作原理[2],基于銅柱測壓的特點和分析方便,提出以下基本假設:

①忽略測壓油管道效應和測壓油的慣性影響;

②將活塞桿視為剛體而不計其變形;

③忽略銅柱內應力波的傳播,在測試過程中銅柱各個截面所受應力在同一時刻相等;

④不計活塞桿受到的摩擦。

3.2 活塞運動方程

圖4為銅柱測壓系統簡化受力模型。

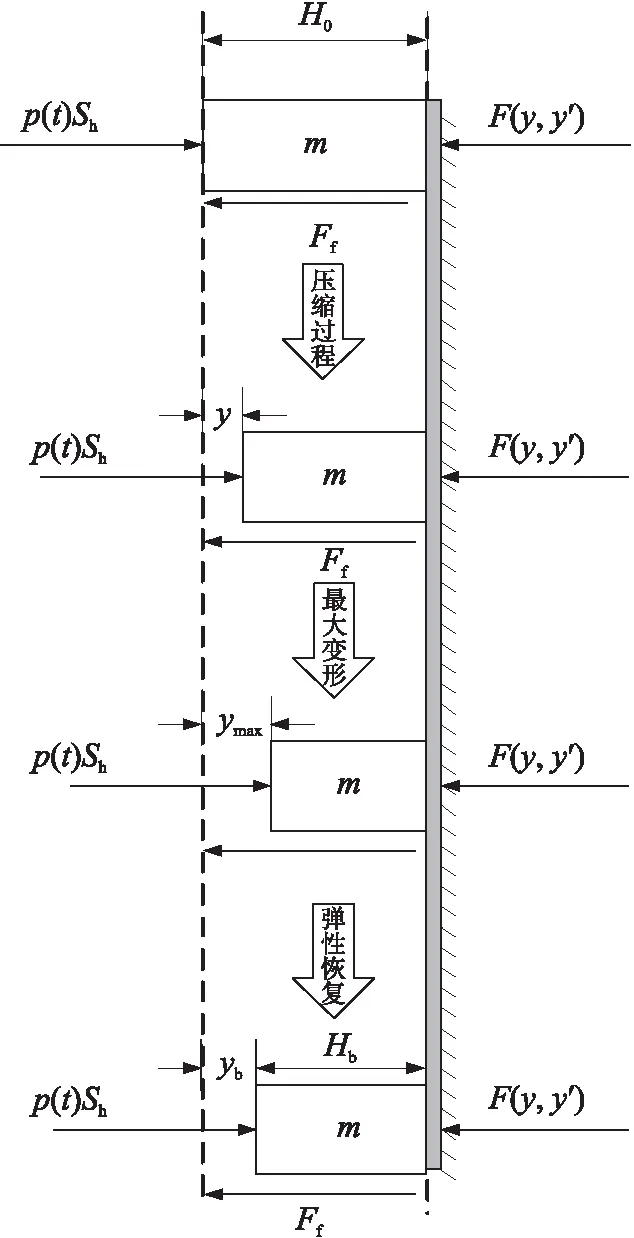
圖4 銅柱測壓系統簡化模型

活塞的運動方程:

(5)

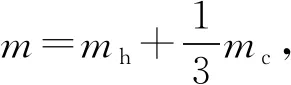
F(y,y′)=Scσ

(6)

式中:σ為銅柱動態應力。

3.3 銅柱的本構方程[4]

(7)

C(ε)=C1e-C2ε+C0

(8)

式中:C0,C1,C2為常數,可通過材料動態性能測試實驗得出。

3.4 變形協調方程

對于預壓銅柱:

(9)

3.5 銅柱靜態應力-應變關系

通常根據銅柱出廠時的靜態壓力與壓后高關系表(pc,Hb)可換算出σc與y的三次函數關系[5]。由于測壓銅柱本身的力學性能具有較好的一致性[6],且在測壓實驗中表現出線性規律,在此可進行簡化,即

(10)

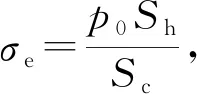
上文中的三階常微分方程初值問題可化為一階常微分方程組的初值問題。

①彈性段。

(11)

初始條件:

結束條件:

y1(t)=ye

以此時刻參數作為塑性段初始條件,同時補充條件y3(0)=0。

②塑性段。

(12)

當已知測壓銅柱的材料參數時,根據內彈道實驗時銅柱的壓后高Hb,t及壓力脈寬即可計算得到內彈道壓力峰值pm,c。計算流程如圖5所示。

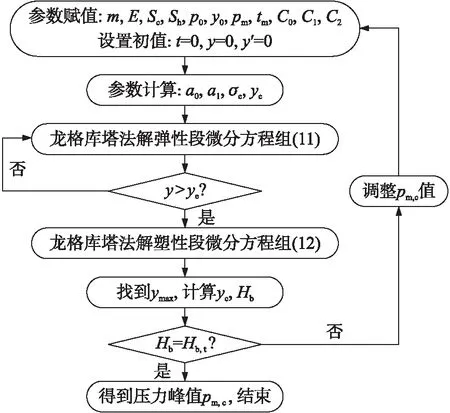
圖5 計算流程圖

4 計算分析

4.1 基本參數

文獻[4]中,選用型號為φ8 mm×13 mm 1201批次的銅柱和電子測壓器,在不同裝藥號下分別進行膛壓測試實驗。通過該批銅柱的壓后高和壓力對照表得到各種裝藥條件下所測壓力pm,t,以電子測壓器所測壓力曲線得到電測壓力峰值pm,e和壓力脈寬tm。

本文以上述實驗的結果為例進行分析,實驗中所使用的銅柱力學性能參數作為計算常量,如表1所示。根據實驗中獲得的電測壓力脈寬[7],以半正弦壓力脈沖作為動態加載的壓力信號,以實驗中的電測壓力峰值和銅柱查表壓力作為參考依據,如表2所示。表中,p0為預壓壓力,Hb,0為預壓后銅柱高度,Hb,t為實驗后銅柱高度,pm,e為電測壓力峰值,tm為電測壓力脈寬。

表1 計算常量

表2 輸入參數[3]

利用表2中的電測壓力及脈寬可以確定實驗中銅柱的平均加載速率范圍為:74.79～131.73 MPa/ms。

4.2 計算結果

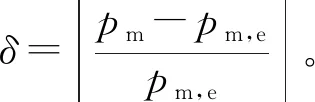
表3 銅柱測壓法與模擬計算的對比

由表3可以看出,在計算壓后高與實驗結果相差0.003 mm以內時,仿真計算的壓力峰值比通過查表獲得的壓力值更接近電測最大壓力,誤差可以減小到3%～10%,但仍存在隨著被測壓力增大誤差也增大的問題。為了進一步減小誤差與誤差帶,借助量綱分析及相似理論[8-10],得出經驗公式:

(13)

(14)

修正后的結果如表4所示,表中,p′m為修正后的壓力峰值,δc為計算壓力峰值相對電測壓力峰值的誤差,δ′c為修正后的壓力誤差。

表4 修正結果

修正后的誤差能夠被控制在±3%以內,尤其是對高壓情況下的預測誤差更是穩定在1.65%左右,說明在內彈道射擊實驗中可以通過這種數據處理方法來提高銅柱測壓法的準確度。由于銅柱測壓本身存在著動態響應性差的固有缺陷,上述公式中的系數僅適用于本文中的加載條件。

5 結論

本文使用銅柱測壓系統的數學模型,進一步考慮了銅柱力學性能的個體差異,通過銅柱預壓過程得到了銅柱的靜態應力-應變關系;采用數值方法計算得到火炮膛壓的峰值,借助量綱分析及相似理論對計算結果進行修正并對高壓實驗進行了預測,結果一致性良好。得到如下結論:

①采用本文提出的最大壓力計算模型,與傳統的一次預壓銅柱測壓法相比,不再需要借助銅柱壓力表,只需要輸入實驗數據即可獲得結果,后續可將整個銅柱測壓實驗中的變形量數據由激光等方式自動化測量直接導入計算機,操作更加簡單;

②在74.79～131.73 MPa/ms的平均加載速率下,提出了銅柱壓力修正公式(14),對高壓情況下預測的壓力誤差顯著小于傳統查表方法,對靶場內彈道實驗有積極意義。