淺談小學計算教學中的算理教學

邢學華

在新課程理念下，計算教學除了要學生理解和掌握算法、形成運算技能外，還要讓學生在經歷算法的探索過程中感悟基本思想、積累基本活動經驗、發(fā)展數學思考能力。學生掌握計算方法的關鍵在于對算理的理解。通過探究，既要讓學生懂得怎樣算，更要讓學生懂得為什么要這樣算。

一、算理是算法的理論依據，為計算提供正確的思維方式

算法解決運算操作的程序與步驟問題，算理解決程序和步驟的道理問題。教學中教師要做到讓學生充分理解算理，為提煉算法作基礎，歸納算法應以理解算理為前提。

例如，青島版五四制教材三年級上冊第71頁信息窗2 “兩位數乘兩位數”的筆算，教師可以通過如下教學，實現算理與算法的融合。

1.以算法承載算理。復習引入時把題中的條件（每排23盆，買了12排）用點子圖表示（每行23個圓點，12行），列出算式后，教師放手讓學生用自己已有認知嘗試計算23×12，并把算理在點子圖上畫出來，讓人一目了然。學生有下面的算法：23×4×3，23×6×2，23×10+23×2，23×6+23×6，23×5+23×7，23×10+23×2。展示交流時，教師要求學生結合點子圖說出為什么這樣算，用自己的語言表達算法背后蘊涵的算理。

2.以算理解釋算法。接著引導比較這些算法的共同點：不論哪種方法，都是先分再合，即先把一個因數分得小些，把兩位數乘兩位數轉化成已學過的兩位數乘一位數，把未知轉化成已知。然后再指導學生用豎式進行計算，并解釋每一步算出的結果分別表示什么。最后引導學生嘗試用“先算……再算……然后……”的句式歸納概括兩位數乘兩位數的計算方法。這樣教學，算理、算法相互溝通融合，算理清、算法明，運用數形結合、轉化思想進行有效數學思考，發(fā)展了學生的遷移推理能力和數學語言表達能力。

二、算法是算理的提煉概括，為計算提供規(guī)范的操作方法

如：在探究兩位數除以一位數的筆算除法時，學生通過知識的遷移、課前預習和自主探究，出現了分小棒、想乘算除、用豎式計算等方法。教學中可以做以下引導。

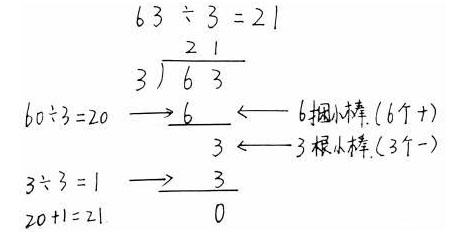
63÷3=

小棒：

引導學生說清：把6捆小棒平均分成3份，每份分得2捆;把3根小棒平均分成3份，每份分得1根。兩次每份共分得21根。

談話：你能用數學的方法將剛才分小棒的過程表示出來嗎？

方法（1）：想乘算除法：因為21×3=63，所以63÷3=21。

方法（2）：60÷3=20，3÷3=1，20+1=21。

引導學生結合小棒圖，說說每個算式的意思。

方法（3）：豎式1：一次除完

評價點落在“沒有呈現兩次分的過程”上。

豎式2：

引導學生對照小棒圖分析每個數表示的含義，引導學生經歷豎式的形成過程。

分小棒的時候，先分6捆，再分3根;在豎式中就要先分6個“十”，再分3個“一”。先分6個“十”，每份分得2個“十”，在十位上商2，有這樣的3份，2個“十”乘3共分掉6個“十”，6減6得0，整捆正好分完;再分3個“一”，每份是1，在個位上商1，3乘1得3，3減3得0，單根正好分完。全部分完后，所得的結果是21。

引導學生思考：2為什么寫在十位？1為什么寫在個位？

回顧整理豎式，第一次除表示了分6捆的過程，第二次除表示分3根的過程。

對比分析：仔細觀察口算方法與豎式方法，看他們有什么聯系？

引導學生發(fā)現：60÷3=20就是第一次除的過程，3÷3=1就是豎式中第二次除的過程，20+1=21就是豎式中的商。

算理：63÷3就是求63平均分成3份，每份是多少？先分6個“十”，6個“十”除以3得2個“十”，在十位寫2， 20乘3得60，十位分完;再分3個“一”，3個“一”除以3得1個“一”，在個位寫1，1乘3得3，個位分完。商是21。

最后引導學生總結算法：

兩位數除以一位數，從十位算起。十位上的商與十位對齊，個位上的商與個位對齊。

學生掌握計算方法關鍵在于對算理的理解。通過探究，既要讓學生懂得怎樣算，更要讓學生懂得為什么要這樣算。所以，運算能力并非一種簡單的、孤立的數學能力，而是運算技能與邏輯思維等的有機整合。