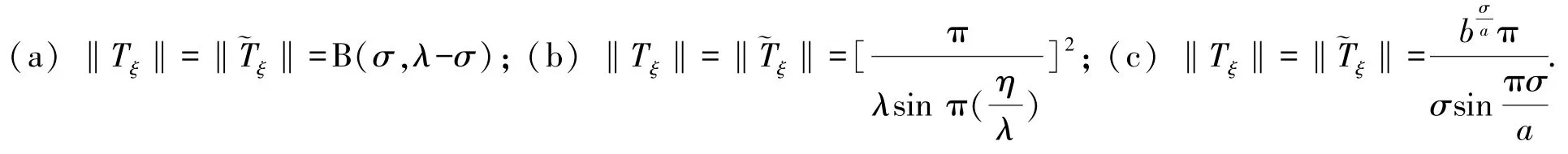一個非齊次核較為精確半離散的Hilbert 型不等式的等價性質

楊必成

（廣東第二師范學院 數學系， 廣東 廣州510303）

0 引言

以上兩不等式是分析學的重要不等式，其推廣應用見文［2－9］.

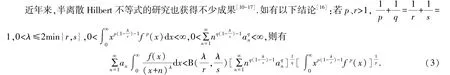
2016 年，洪勇［18］討論了聯系非獨立參數及最佳常數因子的一般齊次核離散Hilbert 型不等式的等價描述.文［19－22］考慮了一些積分的類似工作，但未涉及半離散非齊次核Hilbert 型不等式的等價性問題.

本文應用實分析技巧、權函數方法、參量化思想及Hermite－Hadamard 不等式，給出一個較為精確的半離散一般非齊次核Hilbert 型不等式，同時，還考慮了其等價形式、常數因子取最佳值的聯系參數的等價條件，算子表示及一些特殊形式. 本文的結果可認為是文［18］的思想方法在半離散非齊次核Hilbert 型不等式的有意義拓展，它對同類問題的研究有借鑒意義.

1 引理

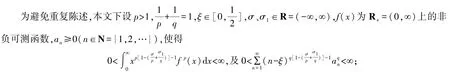
又設函數h（u）在R＋上非負可測，且對η＝σ，σ1∈R，滿足下面條件：

（ii）正常數k（η）表示為

注1對于任意常數η＝，若滿足min｛σ，σ1｝≤≤max｛σ，σ1｝，則仍有上述性質（i）（ii）. 事實上，不失一般性，不妨設σ≤σ1.則有min｛σ，σ1｝＝σ≤~η≤σ1＝max｛σ，σ1｝，函數h（u）u~η－1＝h（u）uσ1－1·u~η－σ1在R＋嚴格遞減且嚴格凸，有

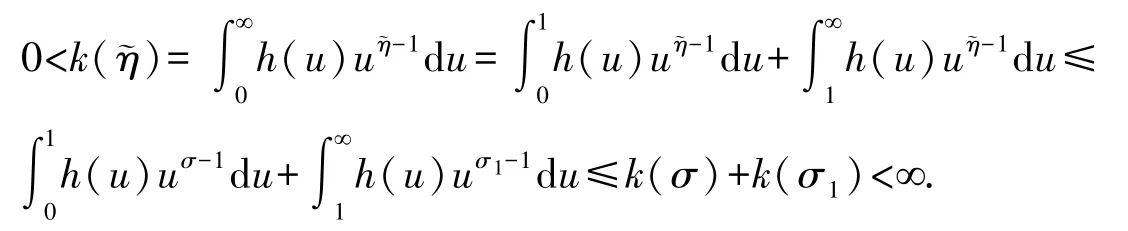
引理1定義如下權函數：

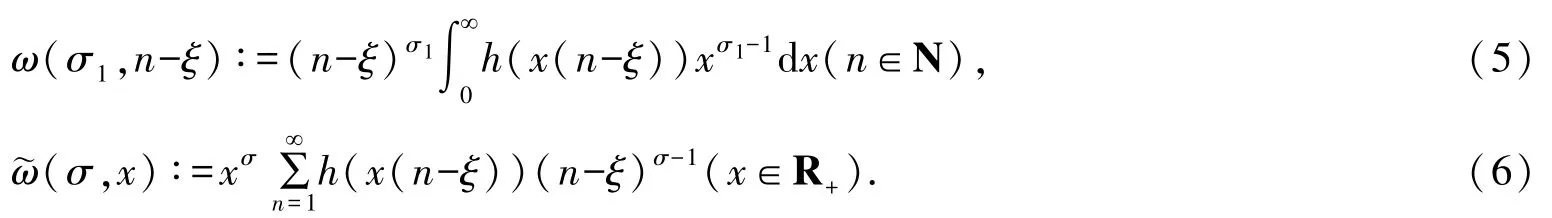
則有如下等式與不等式：

證明作變換u＝x（n－ξ），則有

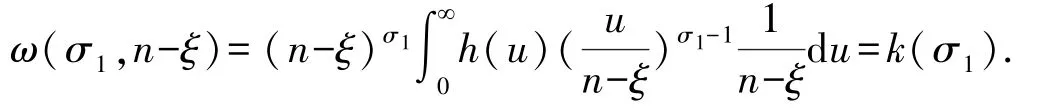
式（7）成立.

由遞減凸條件，應用Hermite－Hadamard 不等式［23］及固定x，作變換u＝x（y－ξ），我們有

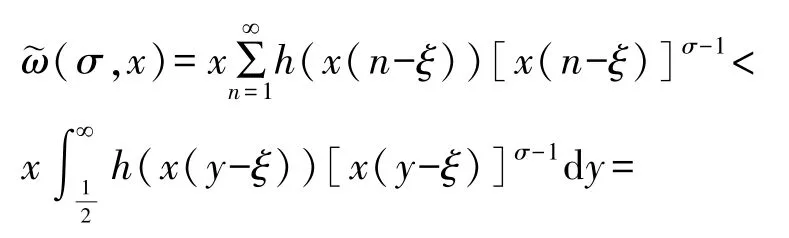
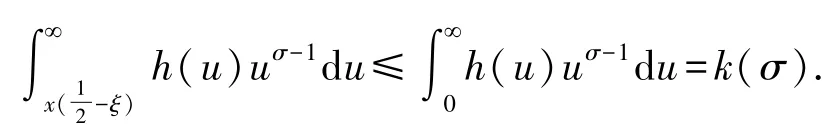
因而有式（8）.證畢.

2 主要結果

定理1式（9）與下列不等式等價：

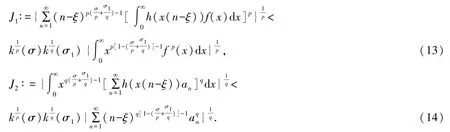
證明設式（13） （式（14））成立，由H?lder 不等式［23］，有

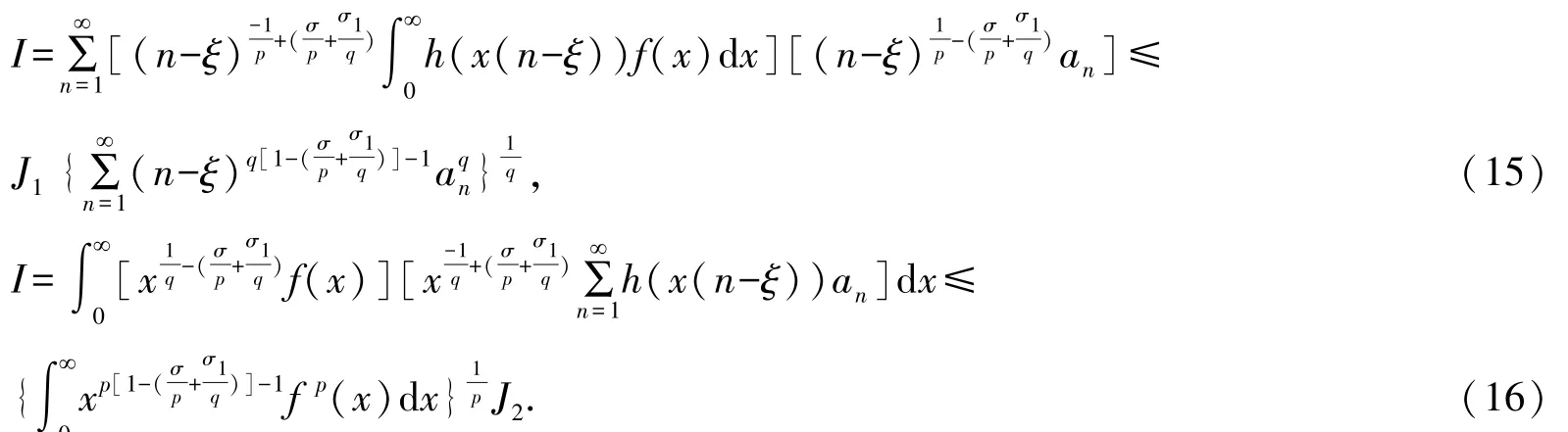
代入式（13）（式（14）），有式（9）.反之，設式（9）成立.置

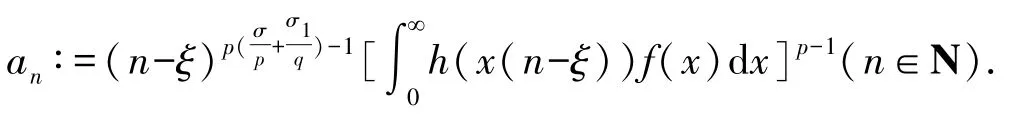
若J1＝0，則式（13）自然成立；若J1＝∞，則不可能使（13）成立，即有J1＜∞.下設0＜J1＜∞，則由式（13），有

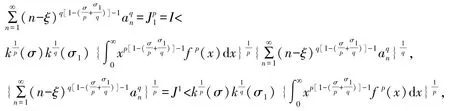
即有式（13），它與式（9）等價.

同理，置

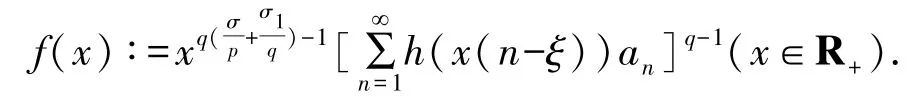
若J2＝0，則式（14）自然成立；若J2＝∞，則不可能使（14）成立即有J2＜∞.下設0＜J2＜∞，則由式（9），有

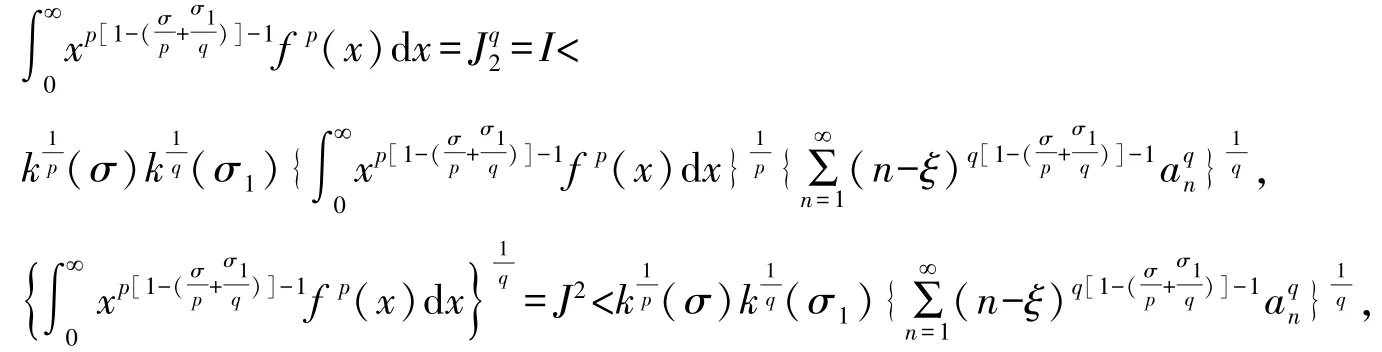
即有式（14），且它與式（9）等價.

故式（9）、式（13）及式（14）齊等價.證畢.

定理2若式（9）的常數因子為最佳值，則式（13）及式（14）亦然，且有σ1＝σ.當σ1＝σ時，式（9）、式（13）及式（14）變為具有最佳常數因子k（σ）的式（10）及如下與之等價的不等式：

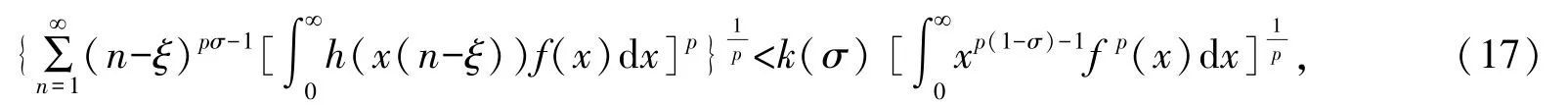
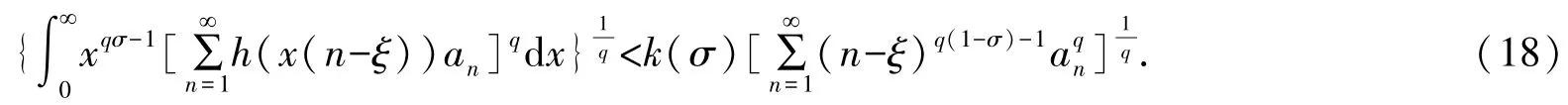
證明設式（9）的常數因子為最佳值.則式（13）（式（14））的常數因子必為最佳值.不然，由式（15）（式（16）），必導致式（9）的常數因子也不為最佳值的矛盾.再由引理3，有σ1＝σ.證畢.

注3由式（9）、式（13）與式（14）的等價性，若此三式之中的任意一式的常數因子為最佳值，則其余二式亦然.

綜合引理3、定理2 及注3，有

定理3若η＝σ1，σ滿足題設（i）（ii）的條件，則等價式（9）、式（13）及式（14）中任意一式的常數因子為最佳值的充分必要條件是σ1＝σ.

3 算子表示及特例

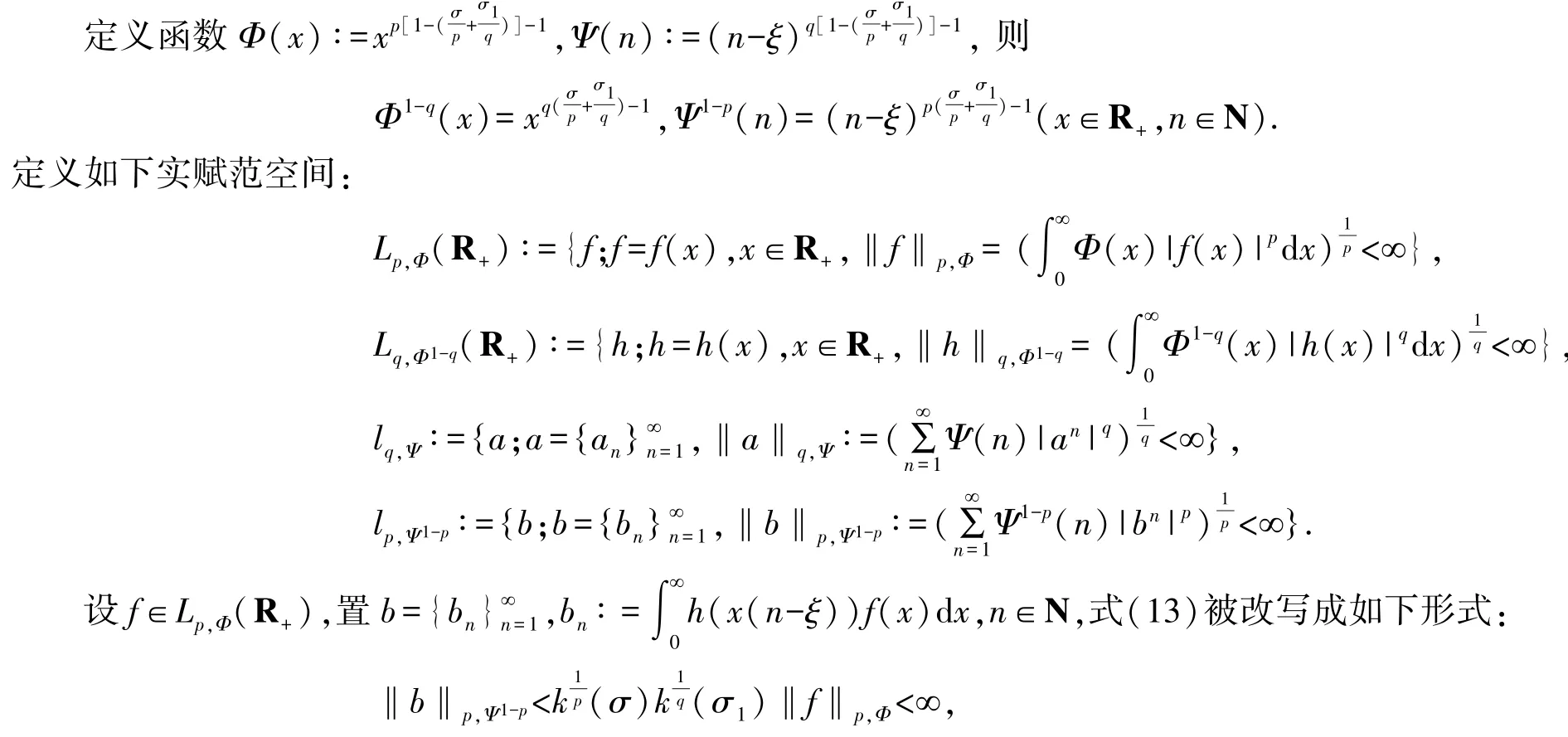
即b∈lp，Ψ1－p.

定義1定義一個較為精確半離散一般非齊次核Hilbert 型算子Tξ：Lp，Φ（R＋）→lp，Ψ1－p為：對任意f∈Lp，Φ（R＋），唯一對應Tξ f＝b∈lp，Ψ1－p.定義Tξ f與a∈lq，Ψ的形式內積及算子Tξ的范數為

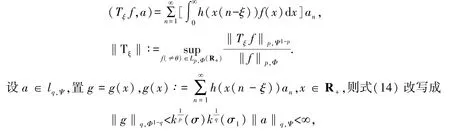
即g∈lq，Φ1－q.

定義2定義一個較為精確半離散一般非齊次核Hilbert 型算子：lq，Ψ→Lq，Φ1－q（R＋）為：對任意a∈lq，Ψ，唯一對應a＝g∈Lq，Φ1－q（R＋）.定義f∈Lp，Φ（R＋）及a的形式內積與算子的范數為

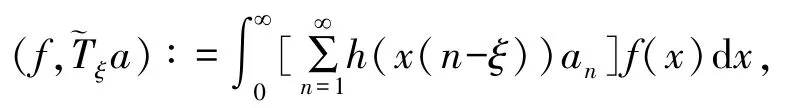
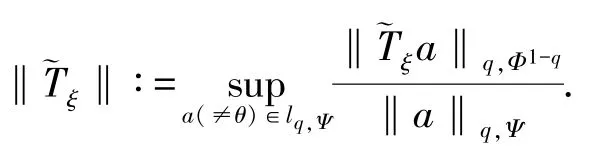
由定理1、定理2 及定理3，有

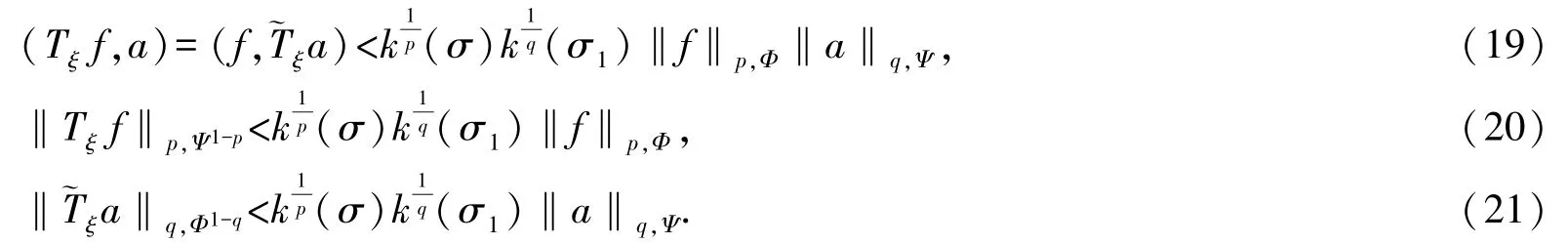
定義4若f∈Lp，Φ（R＋），a∈lq，Ψ，‖f‖p，Φ，‖a‖q，Ψ＞0， 則有如下等價不等式：若式（19）、式（20）及式（21）中任意一式的常數因子為最佳值，則其余二式亦然； 式（19）、式（20）及式（21）中任意一式的常數因子為最佳值當且僅當σ1＝σ.當σ1＝σ時，有及

例1 的（Ⅰ）（Ⅱ）及（Ⅲ）均滿足定理3 的條件，代入式（19）、式（20）及式（21），可得3 組特殊核等價不等式.當且僅當σ1＝σ時，有