關于逆向Hilbert 型積分不等式的一組等價陳述

辛冬梅， 楊必成

（廣東第二師范學院 數學系， 廣東 廣州510303）

0 引言

則有如下具有最佳常數因子kp的Hardy－Hilbert 型積分不等式：

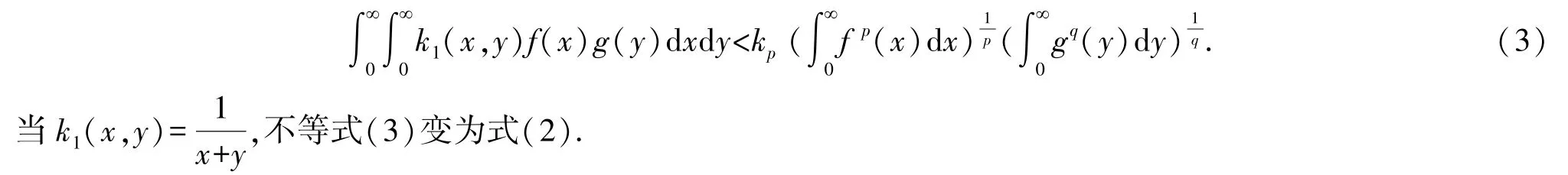
Hardy 等在文［3］定理350 中還建立了如下非齊次核Hilbert 型不等式：若

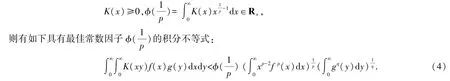
在不等式（3）及式（4）中，若0＜p＜1（q＜0），則還存在逆向的情形.

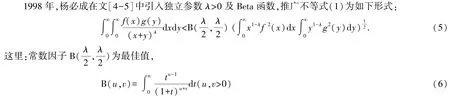
為Beta 函數.

2004 年，楊必成［6］引入兩對共軛指數輔以獨立參數，推廣了不等式（2），且常數因子為最佳值；其后，文［7－10］還給出了該法的其它應用.2016—2019 年，洪勇等［11］給出了一般齊次核離散Hilbert 型不等式常數因子最佳性的聯系參數的等價陳述；洪勇［12］給出了一般齊次核Hilbert 型積分不等式成立的聯系多參數的一個等價條件；楊必成［13－14］考慮了一般齊次核半離散及積分不等式常數因子最佳性的聯系多參數的等價陳述.類似的及逆向的結果可參閱文［15－19］.

本文借鑒文［11］的研究思想，引入多參數，應用實分析的技巧及權函數方法，建立一個一般非齊次核逆向的Hilbert 型積分不等式，考慮了它的等價形式及聯系最佳常數因子與多參數的等價陳述.作為應用，給出了若干特殊核的例子.本文的引理及定理對同一類積分不等式的研究有借鑒意義.

1 若干引理

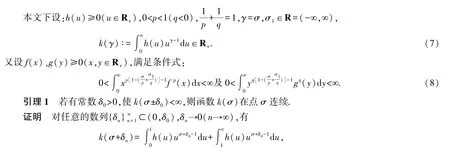
且有如下兩組受控不等式：

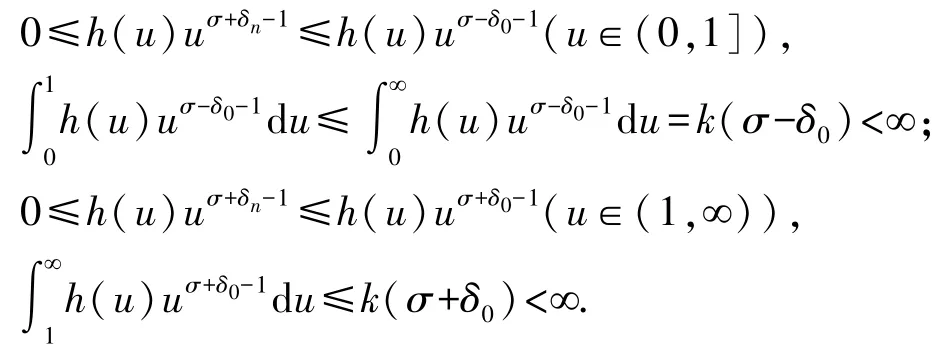
引入如下控制函數：

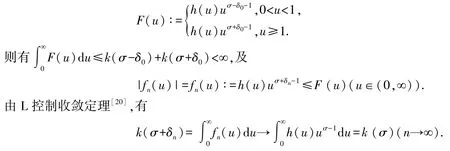
因而函數k（σ）在點σ連續.證畢.

引理2如下逆向的含非齊次核Hilbert 型積分不等式成立：

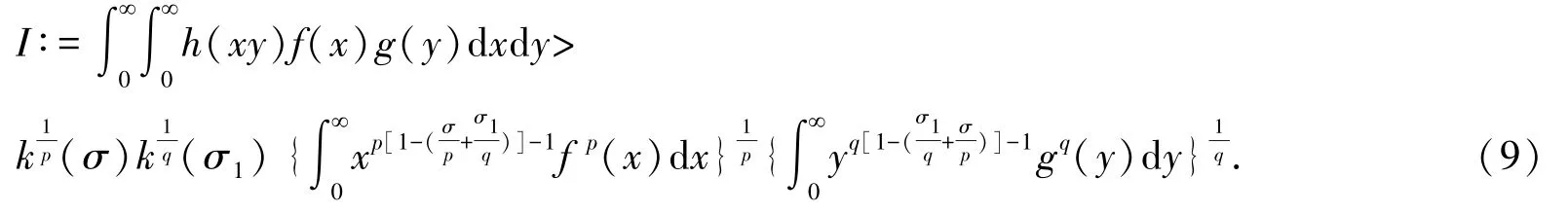
證明定義權函數ω（σ，x）如下：

固定x＞0，對上述積分作變換u＝xy，可算得

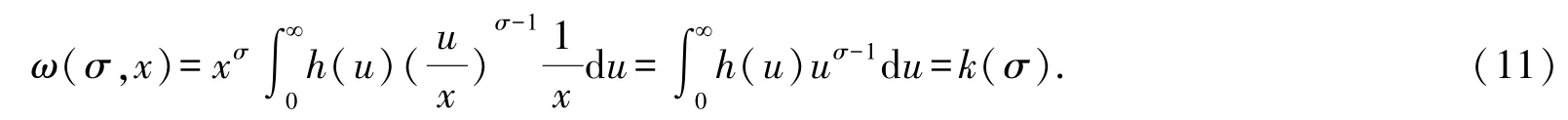
同理，由對稱性，還可求得另一權函數的關系式如下：

配方，應用逆向的H?lder 積分不等式［21］及交換積分次序的Fubini 定理［20］，再由式（10）及式（12），有不等式：

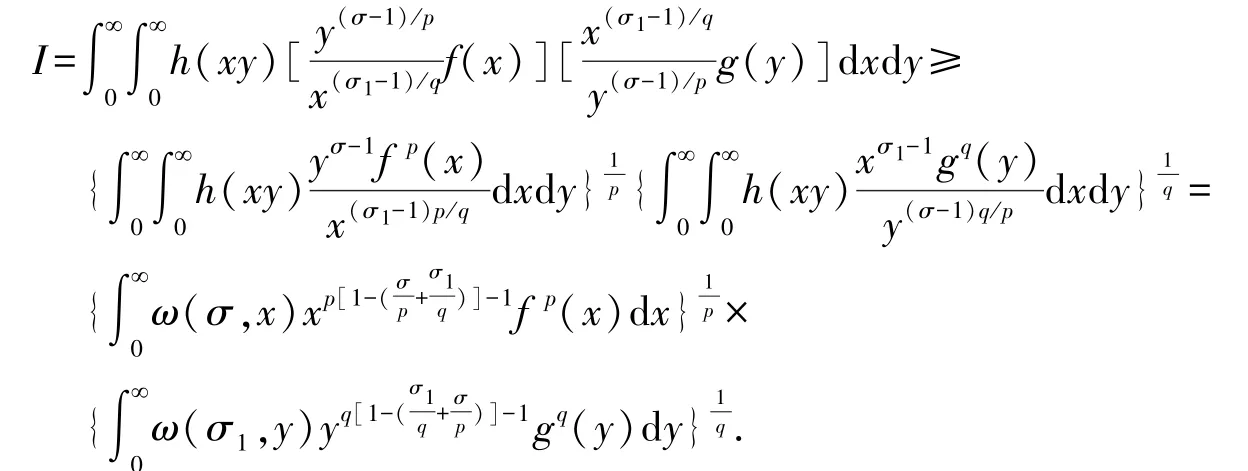
下面用反證法證明此式取嚴格不等號.若取等號，則存在不全為零的常數A和B，使［21］

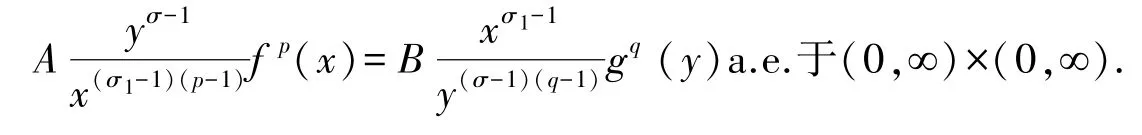
不妨設A≠0.則對于幾乎處處的y∈（0，∞），有

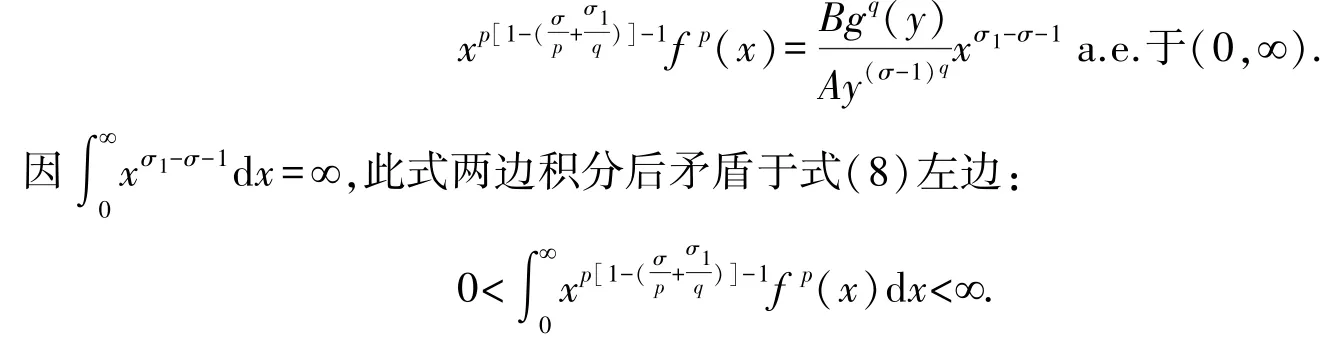
再由式（11）及式（12），可導出式（10）.證畢.

注1若σ1＝σ，則代入式（8）及式（9），有條件式

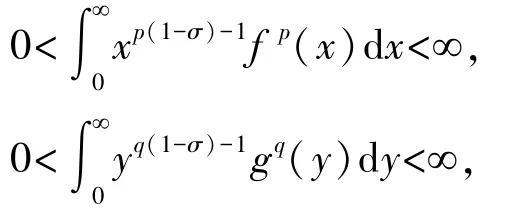
及如下逆向的非齊次核Hilbert 型積分不等式：

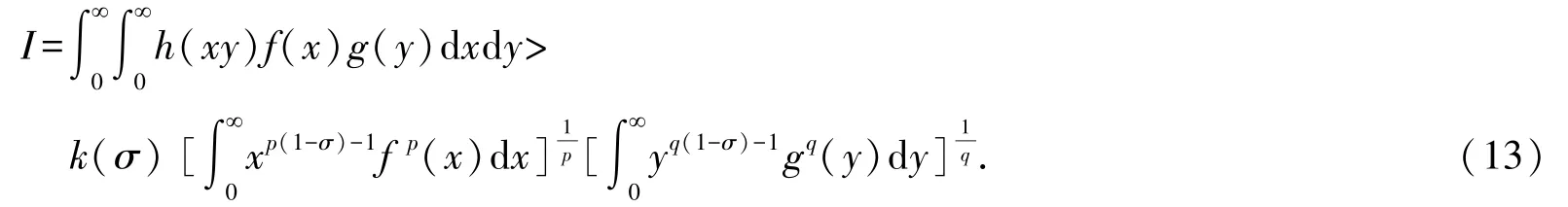
引理3若有常數δ0＞0，使k（σ±δ0）＜∞，則式（13）的常數因子k（σ）是最佳的.

證明任給0＜ε≤pδ0，設如下函數：

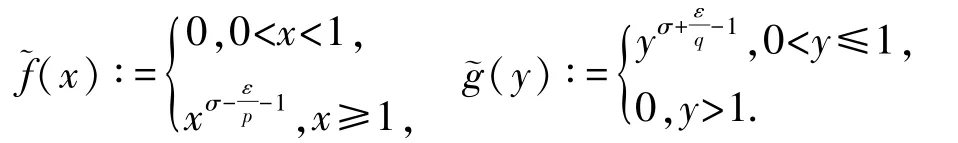
若有常數M（≥k（σ）），使取代k（σ）后，式（13）仍成立，則特別有

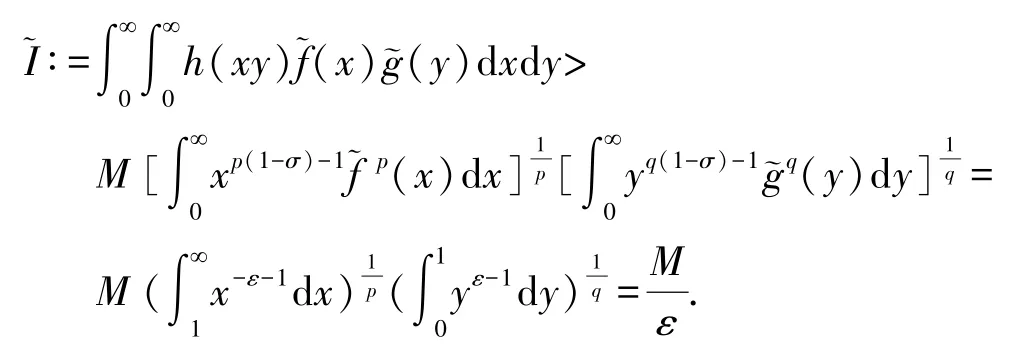
由式（12），還可算得

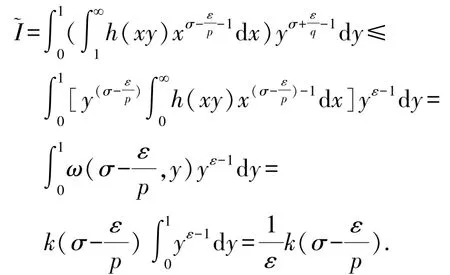
基于上面的結果，有如下不等式：

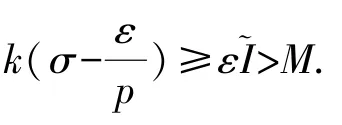
令ε→0＋，由引理1 中k（σ）的連續性，有k（σ）≥M.故常數M＝k（σ）是式（13）的最佳值.證畢.

注2若則它等價于σ－σ1∈（qδ0，－qδ0）.不等式（9）可簡寫為如下形式：

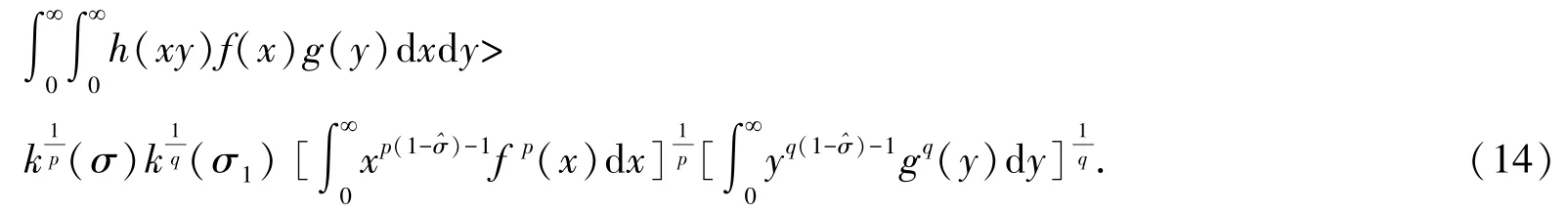
由逆向帶權的H?lder 積分不等式［21］，可得

2 等價形式及等價陳述

定理1不等式（9）與下列逆向的非齊次核Hilbert型積分不等式等價：

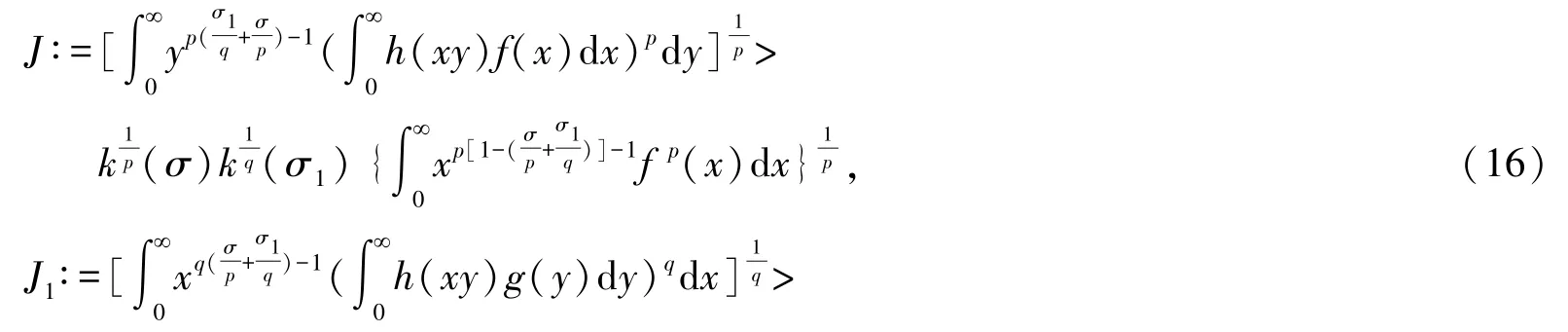
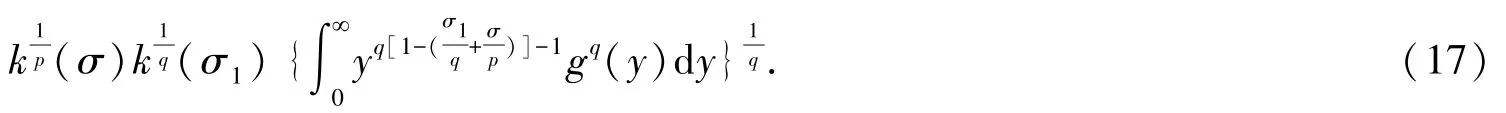
特別地，若σ1＝σ，存在δ0＞0，使k（σ±δ0）＜∞，則成立具有最佳常數因子的式（13）及如下等價的逆向Hilbert 型積分不等式：

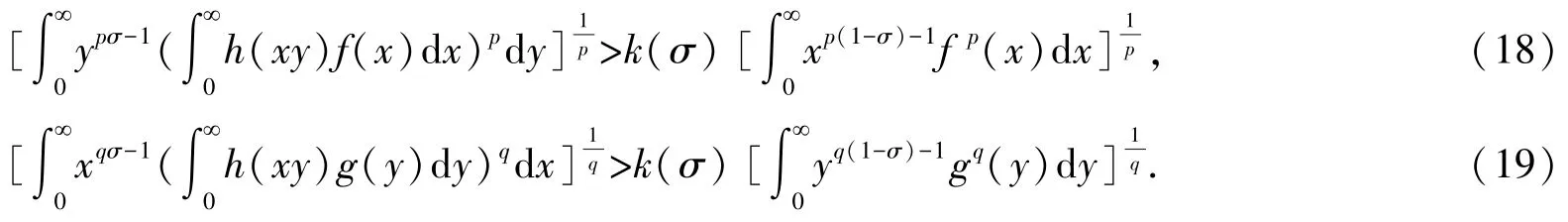
證明若不等式（16）為真，則由逆向的H?lder 積分不等式［20］，有

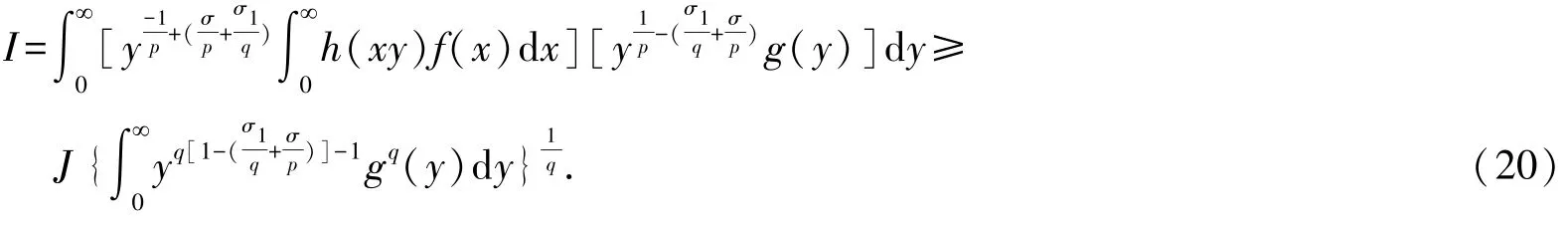
代入不等式（16），有式（9）.反之，設不等式（9）為真.置函數

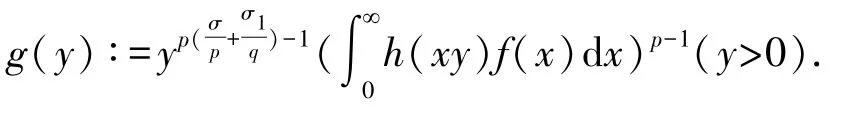
則可得如下等式：

若J＝∞，則不等式（16）自然成立；若J＝0，則不等式（16）必不成立，即有條件式J＞0.下設0＜J＜∞.由不等式（9），有

即有不等式（16），且它與不等式（9）等價.

同理可證，不等式（17）成立且它與不等式（9）等價.于是，不等式（9）、式（16）與式（17）齊等價.

若不等式（9）的常數因子為最佳值，則由式（20）知式（16）的常數因子必為最佳值.不然，則導致式（9）的常數因子不為最佳值的矛盾.同理，若不等式（17）的常數因子為最佳值，則可導出式（9）的常數因子也不為最佳值的矛盾.故不等式（16）及不等式（17）的常數因子是最佳值等價于不等式（9）的相同常數因子也是最佳值.證畢.

定理2若存在常數δ0＞0，使k（σ±δ0）＜∞，則下列陳述等價：

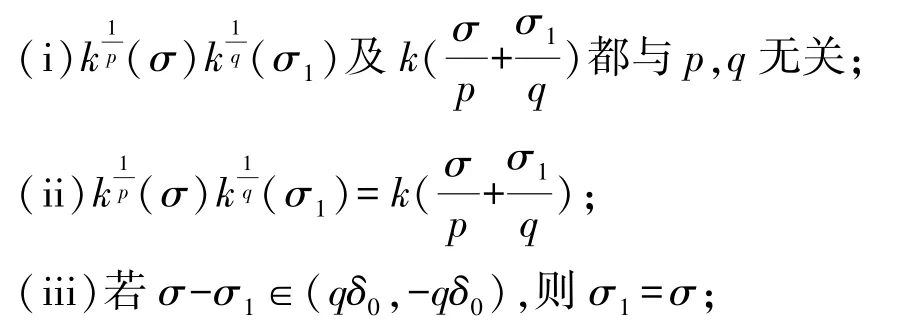
證明（i）?（ii）. 由條件及引理1 中k（σ）的連續性，有

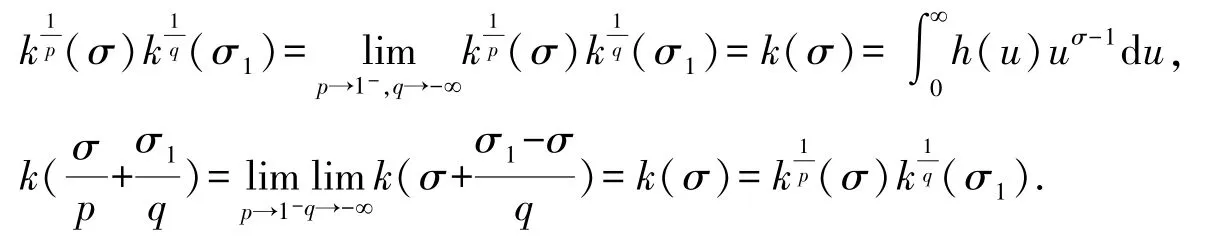
（ii）?（iii）.設則不等式（15）取等號.由引理4，若σ－σ1∈（qδ0，－qδ0），則可得關系式σ1＝σ.

（iii）?（i）. 因σ1＝σ，有

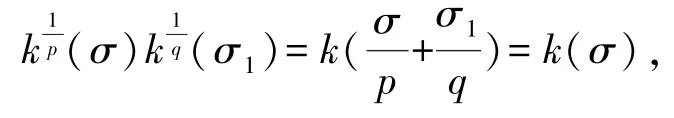
它們與p、q無關.因而（i）?（ii）?（iii）.

（iii）?（iv）. 若σ1＝σ，由引理3 及定理1，不等式（9）、式（16）及式（17）的常數因子（＝k（σ））都為最佳值.

（iv）?（iii）. 由引理4，因σ－σ1∈（qδ0，－qδ0），有σ1＝σ.因而（iii）?（iv）.故陳述（i）（ii）（iii）及（iv）齊等價.證畢.

3 若干特例應用

取δ0∈（0，min｛σ＋α，λ－σ＋α｝）.則有－α＜σ±δ0＜λ＋α，k（σ±δ0）∈R＋.應用定理1 及定理2，可得一些特殊核的結果.