雙單播網絡編碼的構造方法

蒲保興，莫智懿

（梧州學院大數據與軟件工程學院，廣西 梧州 543002）

1 引言

單源網絡編碼[1-3]已經得到了深入廣泛的研究，并獲得了較好的研究成果。對于多源網絡編碼[4]而言，盡管其已被學術界長期關注并被持續地研究，但仍沒有獲得突破性的進展。雖然多源網絡編碼是一個相當困難的問題，但多單播網絡編碼[5]是多源網絡編碼中一種比較容易的情形。文獻[6]的研究表明，任意一個多源有向無環網絡必定存在一個相應的多單播網絡，兩者具有等價的網絡編碼可解性。即如果在其中一個網絡上存在可行的線性網絡編碼傳輸方案，則在另一個網絡上必定存在相應的可行線性的網絡編碼傳輸方案。因此，研究多單播網絡編碼不僅是網絡編碼技術應用于多單播網絡的需要，也是解決一般多源網絡編碼問題的有效途徑。據此，學術界的研究重點已轉移到了多單播網絡編碼的層面上。在多單播網絡編碼中，最簡單的情形是雙單播網絡編碼[7-9]。在已有的研究中，許多學者試圖運用信息論技術及圖論的工具來探索雙單播網絡編碼的可達信息率區域。文獻[10]的研究表明，2個嵌套信息的容量區域是可以描述的，這2個信息中一個被稱為公有消息，另一個被稱為私有消息，其中，公有消息可擁有3個接收者，私有消息可擁有無數個接收者。文獻[11]的研究表明，關于信息的描述，線性網絡編碼對多源網絡是不充分的。文獻[12]推導了雙單播網絡在實現發送速率向量(1,1)的充要條件。文獻[13]提出了雙單播網絡的廣義網絡共享界（generalized network sharing outer bound）。文獻[14]分析了廣義的網絡共享界在某些特殊的雙單播網絡中的緊致性。文獻[15]和文獻[16]針對雙單播網絡編碼的廣義網絡共享界分別給出了代數解析和網絡級聯解析。但文獻[7]已經證明，求解多單播網絡編碼的可達信息率區域是一個NPC問題（non-deterministic polynomial complete problem），即使求解最簡單的雙單播網絡編碼，也是NPC問題。該文還表明，雙單播網絡編碼并不比k（k>2，k是網絡中存在的源-宿對的數目）單播網絡編碼來得容易，即雙單播網絡編碼完全體現了多單播網絡編碼的困難度。在實際應用中，一方面，需要對雙單播網絡編碼進行求解，另一方面，求出其精確解又是一個NPC問題，從而探索出近似的、較優的可行解技術是解決這一問題的有效途徑。

已有的研究盡管關注雙單播網絡編碼的可達信息率區域的計算，但忽略了網絡編碼的構造。由于多源問題的困難性，即使運用信息論或圖論的相關技術能求出近似的可達信息率區域，但針對可達信息率區域中的某一個點（即選定一個特定可行的源點數據發送速率向量），構造相應的可行的網絡編碼數據傳輸方案仍然相當困難。換句話說，若僅估算出了可達信息率區域，針對該區域中的二維向量仍然難以構造相應的網絡編碼數據傳輸方案。這與單源網絡編碼完全不同，對于單源網絡編碼而言，只要源點的數據發送速率不超過最大流-最小割界，則存在有效的算法來構造可行的網絡編碼數據傳輸方案。其主要原因是單源網絡編碼只有一個源點，不存在消息干擾；但對于具有多個源點的網絡而言，宿點接收到的信息是各源點消息的線性組合，即存在消息干擾。若只求出了近似的可達信息率區域，而沒有給出構造傳輸方案的方法，則該方法僅有理論價值，沒有實際應用的價值。因此，從實際應用的角度出發，應該把這2個問題給合起來進行研究，不僅要給出近似的可達信息率區域，還要給出可達信息率區域中各發送速率向量對應的網絡編碼數據傳輸方案。

解決雙單播網絡編碼問題的關鍵是讓宿點消除干擾，文獻[9]運用源點預編碼策略作用于雙單播網絡的信息不等式提出了求解雙單播網絡編碼近似可達信息率區域的方法，但該方法僅對文獻[17]提出的雙單播網絡的可達信息率區域所滿足的信息不等式實現了可計算化，未涉及網絡編碼的構造。

本文的貢獻如下。基于文獻[9]的思想，即在源點進行預編碼，使宿點接收到的全局編碼矩陣的某些列強迫為全零列，把文獻[18]提出的線性網絡編碼的導出技術由單源情形擴展到了雙單播網絡情形，并從源點預編碼和信息熵的角度嚴格證明了導出技術的正確性。在此基礎上，本文采用多目標優化進化算法并結合隨機線性網絡編碼技術來形成傳輸方案，提出了選擇預編碼矩陣的策略：用宿點的信息轉換矩陣的零向量空間的基向量和行向量空間的基向量共同來確定預編碼矩陣的列向量，從而使宿點的全局編碼矩陣的某些列變為全零列，在宿點消除了部分信息干擾。根據雙單播情形下的網絡編碼的導出技術，運用二級預編碼策略來控制源點的發送速率。結合以上策略，本文提出了雙單播網絡編碼的構造方法。所提方法不僅能求出雙單播網絡編碼的近似可達的信息率區域，同時針對求出的可達信息率區域中的任何一個整數坐標點，還提供了構造可行的網絡編碼數據傳輸方案的具體方法。

2 預備知識

雙單播網絡編碼[8]。在一個有向無環網絡G=(V,E)中，V為節點集，E為有向邊集。假設網絡中有向邊的容量為整數，單位容量的有向邊稱為信道，若有向邊的容量大于1，則被看作多條單位容量的信道。網絡中有2個源點{s1,s2}?V，2個宿點{t1,t2}?V，宿點ti(i=1,2)只需要接收來自源點si的信息，在數據傳輸過程中共享網絡的傳輸資源，網絡的中間節點運用網絡編碼技術來轉發數據。雙單播網絡編碼如圖1所示，其中，Xi(i=1,2)表示源點si發送的字符向量，Yi=M1iX1+M2iX2表示宿點ti接收到的字符向量，其具體的含義見后續的說明。

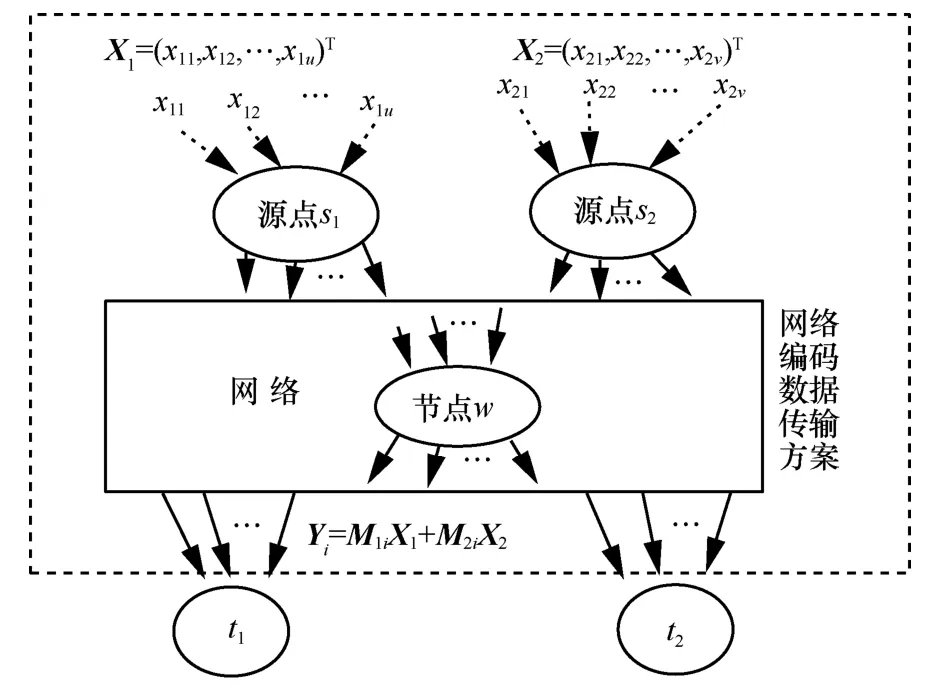
圖1 雙單播網絡編碼

網絡編碼的工作機理[1]如下。選定有限域GF(q)（其中q為2的冪），在一次數據傳輸過程中，源點s1發送了有限域GF(q)中的u個字符至網絡，這u個字符形成一個字符向量，記為X1，如式(1)所示。

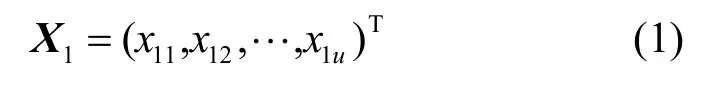
源點s2發送有限域GF(q)中的v個的字符至網絡，這v個字符形成一個字符向量，記為X2，如式(2)所示。

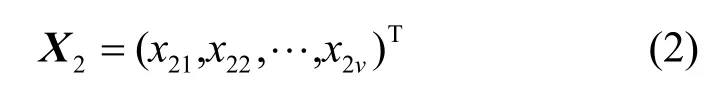
把2個源點發送的字符看作一個u+v維的列向量，如式(3)所示。

為了描述方便，本文認為源點s1發送的u個字符由源點s1的u條虛擬輸入信道分別輸入；源點s2發送的v個字符由源點s2的v條虛擬輸入信道分別輸入。由此可知每一個節點（包括源點）均具有輸入信道，如圖1所示。在數據傳輸過程中，各中間節點（不包括宿點）把從其輸入信道接收到的字符經線性組合后再轉發至該節點的輸出信道。對于每一條信道ei∈E（記信道的尾節點tail(ei)=k，信道的頭節點head(ei)=l，其中，k,l∈V），該信道上傳輸的字符記為，則根據文獻[1]，通過式(4)計算，稱為信道ei的局部編碼向量。

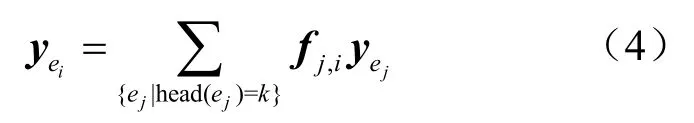
定義1對于雙單播網絡編碼，所有節點的輸出信道的局部編碼向量組成一個集合，稱為網絡編碼數據傳輸方案。

在本文中，網絡編碼數據傳輸方案用符號θ表示，為了敘述簡潔，簡稱為“傳輸方案θ”。

由于有向無環圖的拓撲特征，按照網絡節點的拓撲順序，節點輸出信道傳輸的字符按式(4)進行遞歸與迭代運算，則每一信道所傳輸的字符必定能表示成源點所發送的信息字符的線性組合，如式(5)所示。

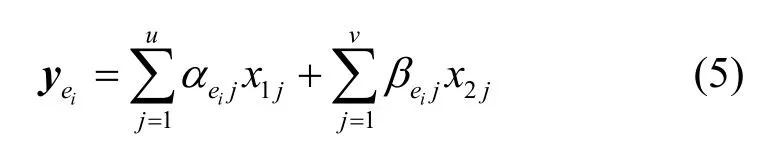
其向量形式如式(6)所示。

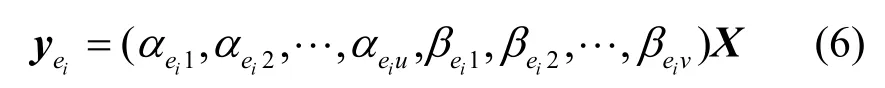
其中，X是源點發送的字符向量，如式(3)所示。稱為信道ei的全局編碼向量。對于網絡中的任意一個節點，把其每一條輸入信道的全局編碼向量作為矩陣的一行，形成一個矩陣，則這個矩陣為該節點的全局編碼矩陣。

由前文可知，式(5)或式(6)描述了信道ei傳輸的字符、信道的全局編碼向量和源點發送的字符向量X三者之間的數學關系。類似于計算信道傳輸的字符，信道的全局編碼向量可以按式(7)進行計算。

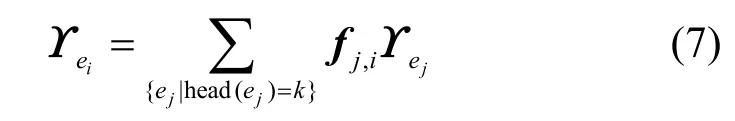
如果采用隨機線性網絡編碼方法傳輸數據，則信道ei傳輸的信息包括兩方面的內容：信道傳輸的字符和信道的全局編碼向量，它們分別通過式(4)和式(7)進行計算。

在按式(4)和式(7)所示的遞歸與迭代計算過程中，根據網絡的拓撲順序，首先需要計算源點輸出信道的全局編碼向量和傳輸的字符，源點s1的u條虛擬輸入信道攜帶的字符分別為x11,x12,…,x1u，則它們的全局編碼向量分別為u+v維的單位向量，其中第i(i=1,2,…,u)條虛擬輸入信道的全局編碼向量的第i個分量為1，其余分量為0。則源點s1的全局編碼矩陣為(Iu×u0u×v)，其中，Iu×u是u階的單位矩陣，0u×v是u行v列的零矩陣。

同理，源點s2的全局編碼矩陣為(0v×uIv×v)。

對于某一個宿點ti，選定δi條輸入信道，根據式(6)的對應關系，把輸入信道的全局編碼向量、信道傳輸的字符、源點發送的字符進行關聯，將形成一個線性方程組。宿點ti的δi條輸入信道的全局編碼矩陣的分塊矩陣形式為(Mi1M2i)，宿點ti的δi條輸入信道所傳輸的字符形成的向量為Yi，則Yi可以通過式(8)進行計算。

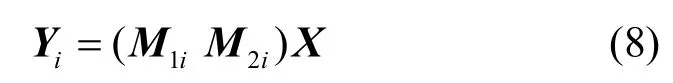
其中，Yi是一個δi維的列向量；(Mi1Mi2)是一個δi行u+v列的矩陣，M1i是源點s1的虛擬輸入信道至宿點ti的消息轉換矩陣，M2i是源點s2的虛擬輸入信道至宿點ti的消息轉換矩陣。Yi、M1i和M2i中的元素均為有限域GF(q)中的字符。

如前所述，由于源點s1的全局編碼矩陣為(Iu×u0u×v)，源點s2的虛擬輸入信道的全局編碼矩陣為(0v×uIv×v)，在傳輸方案θ指引下，各信道的全局編碼向量按式(7)進行計算。注意到，式(7)與式(4)的形式相同，式(7)是在式(4)的基礎上把信道上傳輸的字符yej換成信道的全局編碼向量，從而宿點ti的全局編碼矩陣的計算為

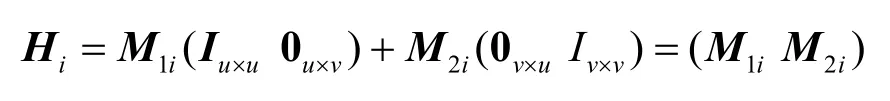
這就表明，分別按式(4)和式(7)計算信道攜帶的字符和全局編碼向量能夠滿足式(5)的對應關系，因此可得式(8)即為宿點ti所析出的線性方程組。

性質1選擇雙單播網絡的傳輸方案θ，則宿點ti(i=1,2)的全局編碼矩陣(M1iM2i)由傳輸方案θ唯一確定。

采用網絡編碼技術傳輸數據必須要構造網絡編碼數據傳輸方案θ，即確定各信道的局部編碼向量，也稱為網絡編碼構造。構造傳輸方案包括2個任務：首先要確定源點的數據發送速率，然后針對選定的源點數據發送速率來確定各信道的局部編碼向量。對于雙單播網絡，因有2個源點，2個源點的數據發送速率形成了一個二維向量，稱之為源點數據發送速率向量。選定了源點數據發送速率向量后，接下來的任務是如何確定傳輸方案θ，按照傳輸方案θ中指定的局部編碼向量進行數據傳輸后，使宿點能夠通過求解線性方程組來恢復源點發送的消息。

定義2針對雙單播網絡，對于給定的源點數據發送速率向量(u,v)，若存在相應的傳輸方案，使宿點通過解碼能獲得所需的消息，則稱(u,v)是可達的，該傳輸方案是可行的，所有可達的源點數據發送速率向量組成的集合稱為可達信息率區域[4]。

解決雙單播網絡編碼的構造問題首先需要確定可達信息率區域，然后針對可達信息率區域中的每一點，再構造相應的可行的傳輸方案。因為存在s1—t1和s2—t2這2個會話，它們共享網絡資源，形成了一種競爭的態勢，從而求解雙單播網絡編碼的可達信息率區域的問題是一個雙目標優化問題，可達信息率區域是雙目標優化問題的Pareto集。

設源點si至宿點ti的最大流為min-cut(si,ti)（i=1,2），記k1-1=min-cut(s1,t1)，k2-2=min-cut(s2,t2)。記{s1,s2}至t1的最大流為k12-1,｛s1,s2｝至t2的最大流為k12-2。由最大流最小割定理，可限制源點s1的數據發送速率的取值范圍為[0,k1-1]。同理，可限制源點s2的數據發送速率的取值范圍為[0,k2-2]。本文只考慮源點發送速率為整數的情況。

本文采用以下策略來尋求可達信息率區域：選定(u,v)∈([0,k1-1]×[0,k2-2])，其中，u和v均為整數。針對源點數據發送率向量(u,v)尋找可行的數據傳輸方案，如能找到，則(u,v)是可達的，記下相應的網絡編碼數據傳輸方案。對所有(u,v)∈([0,k1-1]×[0,k2-2])進行判斷，則可以獲得可達信息率區域。

宿點需要通過解碼獲得源點發送的消息，則必須求解式(8)所示的線性方程組。將式(8)表示為AX=B的形式，其中系數矩陣A=(M1iM2i)為m行n列矩陣，n=u+v。

若系數矩陣A中某一列的元素全為零，則稱之為全零列，表明該列對應的未知量不存在，其含義為該列所對應的由源點發送的字符沒有傳輸至宿點，只有系數矩陣的非全零列才對應一個未知量。關于線性方程組求解，文獻[20]給出了如下定理。

定理1記rank(A)為矩陣A的秩，對于線性方程組AX=B，若系數矩陣不存在全零列，則線性方程組有解的充要條件為rank(A)等于系數矩陣的列數。

針對系數矩陣存在全零列的情況，有如下推論。

推論1對于線性方程組AX=B，記π(A)為矩陣A中非全零列的列數，則線性方程組有解的充要條件為rank(A)=π(A)。

推論1的成立是明顯的，因為只要去掉系數矩陣的全零列，同時去掉全零列所對應的未知量，則可以滿足定理1的條件。

下面，敘述矩陣的行空間與零空間的概念[20]。矩陣A的列空間就是由矩陣A的列向量所張成的m維向量空間的一個線性子空間，記為R(A)；矩陣A的行空間就是由矩陣A的所有行向量所張成的n維向量空間的一個線性子空間，記為R(AT)。

矩陣A的零空間是由齊次線性方程組AX=0的所有解張成的n維向量空間的一個線性子空間，記為N(A)。由零空間的定義可得，對于任意的y∈N(A)，滿足AY=0。

根據線性代數的理論可知，矩陣A的行空間與零空間互為正交補，矩陣A的行空間與零空間的和構成了n維的向量空間。

3 源點預編碼技術及網絡編碼的導出

3.1 源點的預編碼

如圖1所示，選擇傳輸方案θ，宿點t1選定其k12-1條輸入信道，宿點t2選定其k12-2條輸入信道（即根據式(8)可知，宿點t1和t2對應的線性方程組分別為

如前所述，Mij(i,j=1,2)是源點i至宿點j的信息轉換矩陣。其中，M11是k12-1行u列矩陣，M21是k12-1行v列矩陣。M12是k12-2行u列矩陣，M22是k12-2行v列矩陣，Y1和Y2分別是k12-1維和k12-2維的列向量。由性質1，Mij(i,j=1,2)由傳輸方案θ唯一確定。

傳輸方案θ中是在源點實施預編碼。源點的預編碼不是直接把消息字符分別注入源點的虛擬輸入信道，而是把消息字符經過線性組合后再分別注入源點的虛擬輸入信道，如圖2所示。

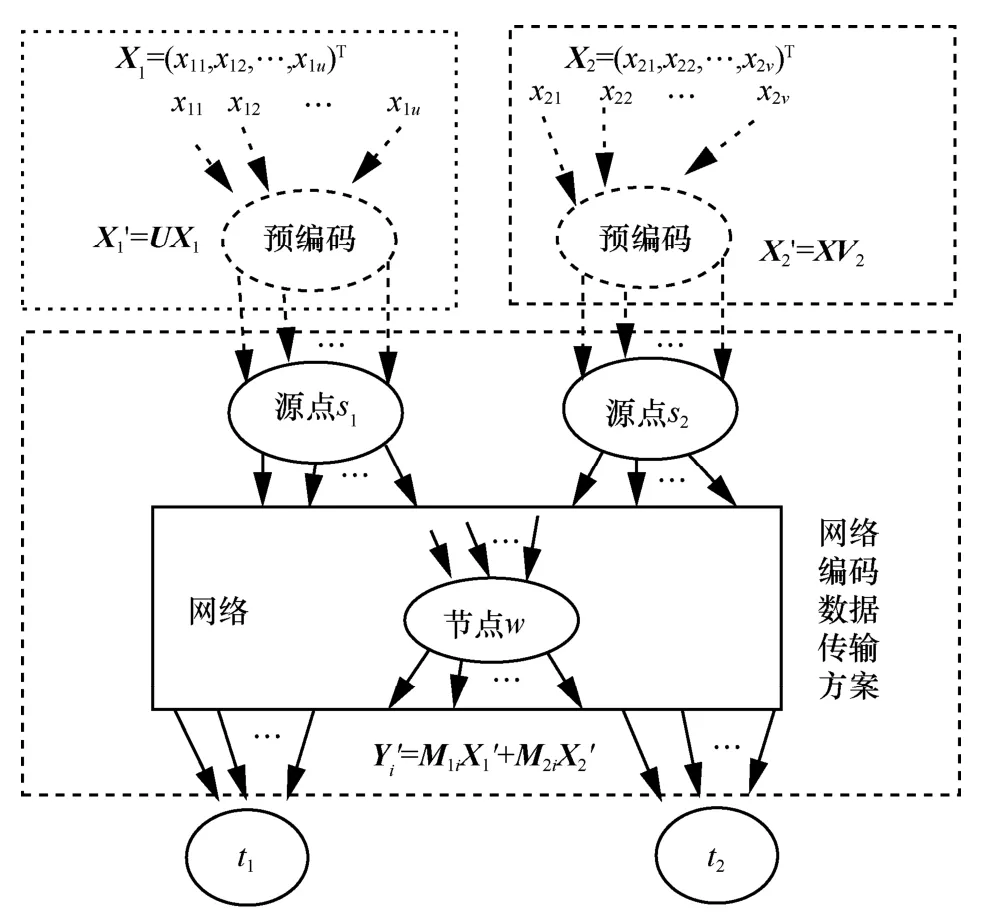
圖2 雙單播網絡編碼的源點預編碼

對于源點s1，假設要傳輸的消息字符向量如式(1)所示，先對這u個字符進行預編碼，其編碼方式如下。

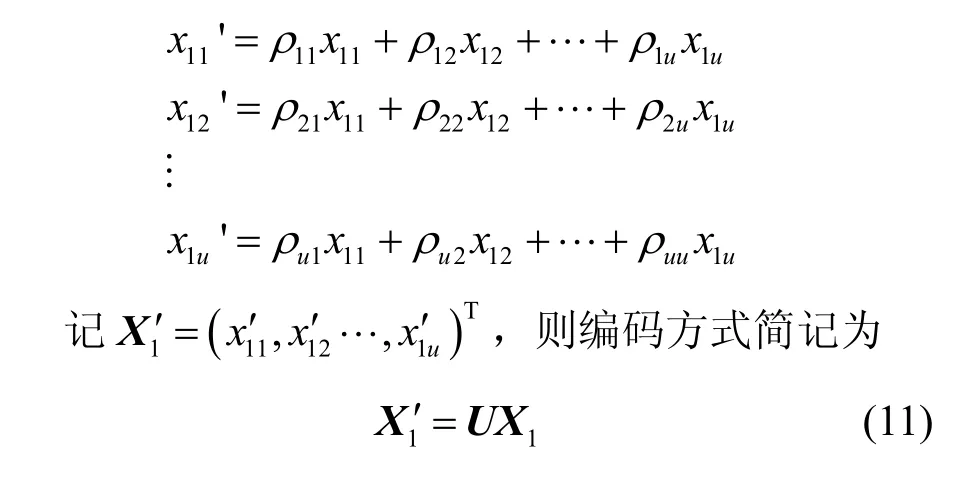
其中，U表示一個u階方陣，每一個系數均為有限域GF(q)的元素，也稱為預編碼矩陣。

同理，可以在源點s2實施預編碼，設預編碼矩陣為v階方陣V，經預編碼后形成的字符向量如式(12)所示。

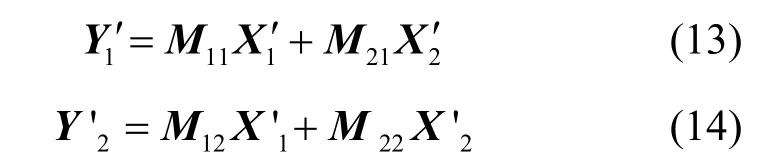
3.2 網絡編碼的導出

文獻[18]提出了單源多播網絡的線性網絡編碼的導出與擴展技術，本文利用源點的預編碼技術提出雙單播網絡的線性網絡編碼的導出技術。

定義3若u,v,u1,v1均為整數，且滿足u1≤u，v1≤v，則稱(u1,v1)受控于(u,v)，也稱(u,v)控制(u1,v1)，記為(u1,v1)?(u,v)。

定義4對于雙單播網絡的一個源點發送速率向量為(u,v)的傳輸方案，在源點s1和s2分別實施式(11)和式(12)所示的預編碼，則從傳輸方案θ中導出了一個新的傳輸方案，本文稱前者為原始方案，后者為導出方案。

定理2線性網絡編碼的導出。若一個雙單播網絡編碼的源點發送率向量(u,v)是可達的，則對于任意(u1,v1)，且(u1,v1) ?(u,v)，(u1,v1)也是可達的，且從源點可達的發送速率向量(u,v)的任何一個可行的網絡編碼數據傳輸方案可以導出(u1,v1)的一個可行的網絡編碼數據傳輸方案。

證明由于(u,v)是可達的，必存在一個可行的傳輸方案θ。在其指引下，宿點t1和t2對應的線性方程組分別如式(9)和式(10)所示。在此基礎上，分別對源點s1和s2實施如式(11)和式(12)所示的預編碼，預編碼矩陣U和V表示如下。

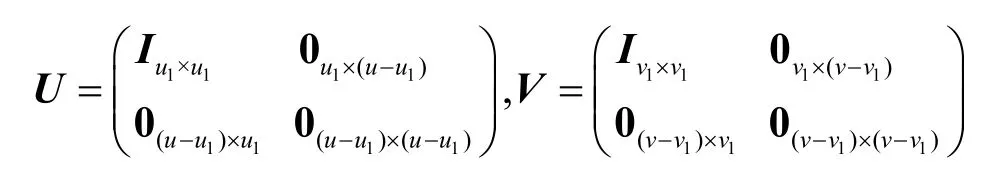
則宿點t1和t2分別得到如式(13)與式(14)所示的線性方程組。由于θ是關于(u,v)的一個可行傳輸方案，則式(9)和式(10)能解出X1和X2。

比較式(9)和式(13)所代表的線性方程組，兩者具有相同的系數矩陣，只是未知量與常數項不同，由推論1，則式(9)和式(13)代表的線性方程組具有相同的可解性，同理，式(10)與式(14)表示的線性方程組也具有相同的可解性。因此，式(13)和式(14)能解出這說明了源點s1實際上僅向網絡傳輸了字符向量且宿點t1能解碼出同理，源點s2實際上僅向網絡傳輸了字符向量且宿點t2可以解碼出由此說明，源點發送速率向量(u1,v1)是可達的，而且通過源點的預編碼，可從可達信息率向量(u,v)的一個可行的傳輸方案θ導出關于(u1,v1)的一個可行的傳輸方案，且導出的傳輸方案僅在源點實施預編碼，其余信道的局部編碼向量與傳輸方案θ相同。證畢。

假設源點產生的消息字符是隨機變量，且相互獨立，每個字符均勻地在有限域GF(q)上選取，若向量X1的維數為u、向量X2的維數為v，根據信息論可知，H(X1)=uq，H(X2)=vq（注：H(·)表示隨機變量的香農信息熵，I(·;·)表示2個隨機變量的互熵）。

定理3對于一個源點的發送速率向量為(u,v)的可行傳輸方案，可以導出一個源點發送速率向量為(u1,v1)的可行傳輸方案，其中(u1,v1)?(u,v)。導出的傳輸方案只需在源點實施預編碼，其他信道的局部編碼向量保持不變，且源點s1的預編碼矩陣U為u階方陣，U的后u～u1列均為全零列，且滿足rank(U1)=u1；由對稱性，源點s2的預編碼矩陣V為v階方陣，V的后v～v1列均為全零列，且滿足rank(V)=v1。

證明源點經過預編碼后，2個源點實際上是分別把傳送到網絡中，首先證明經過預編碼后源點的實際發送率向量為(u1,v1)。為證明這一結論，只需計算的熵。由于U的后u～u1列為全零列，則

另一方面，由于U的秩為u1，根據矩陣代數的理論，則可以從U中的行向量中找到u1行，成為U的行向量的極大無關組，本文記它們的行下標分別為則這u1行對應于的u1個分量，這u1個分量按式(15)所示的對應關系的矩陣形式為

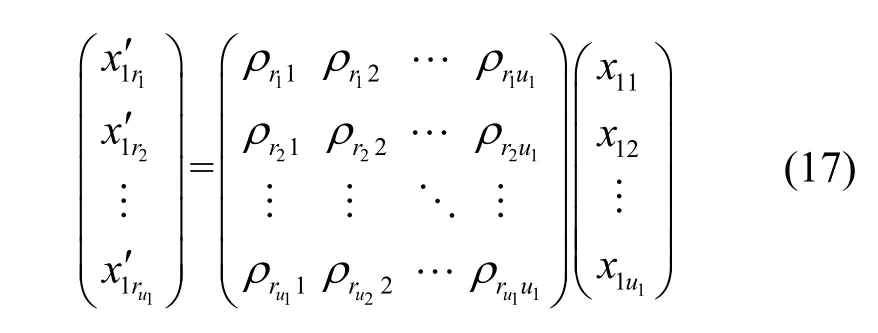
由于極大無關組對應行向量是線性無關的，式(17)中的u1階矩陣是可逆的。求解式(17)所示的線性方程組，可得的每個分量可以被線性表示，因此Z1也是的函數，與上述證明類似，可以得到

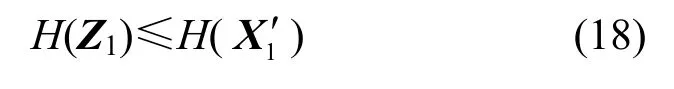
由于式(9)和式(13)具有相同的可解性，經源點預編碼后，宿點t1可以求解式(13)所示的線性方程組得到，利用式(17)，宿點可以恢復出字符向量Z1；同理，宿點t2可以恢復出字符向量從而通過源點的預編碼技術導出了一個源點發送率向量為(u1,v1)的可行的傳輸方案。證畢。

4 基于源點預編碼的宿點干擾消除

在源點實施預編碼后，宿點t1和t2分別得到式(13)和式(14)所示的線性方程組。把式(11)和式(12)分別代入式(13)和式(14)，則得到

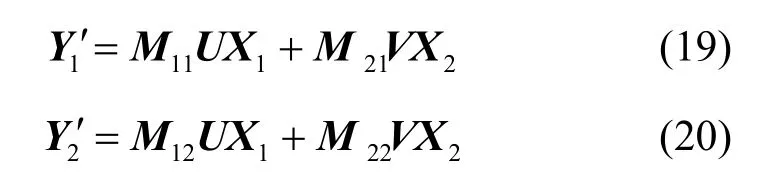
要使式(19)和式(20)能求解，則需要滿足推論1，必須讓系數矩陣的非全零列的數目π(A)與矩陣的秩相等。根據秩的性質，有rank(A)≤π(A)；當rank(A)<π(A)時，因矩陣的秩不會增加，則應減小π(A)的值。如果適當地選取預編碼矩陣的元素，使式(19)和式(20)的系數矩陣出現全零列，從而達到了減小π()A的目標。

宿點t1對應的系數矩陣為其中，M11U和向量X1對應，而X1中的分量是宿點t1所需要的消息；和向量X2對應，X2是宿點t1不需要的，可以看作信息干擾。因此，要使矩陣A出現全零列，應在中出現，且U應為滿秩矩陣；同理，對于宿點t2，應讓M12U出現全零列，且V應為滿秩矩陣。

基于以上分析，預編矩陣U的選取方法如下。首先求M21的行空間再求矩陣M21的零空間注意這2個子空間互為正交補，因M21的列數為v，從而的一組基向量，的一組基向量，則構成了GF(q)域上v維線性空間的一組基向量，令預編碼矩陣V的列向量分別取上述的基向量，如式(21)所示。

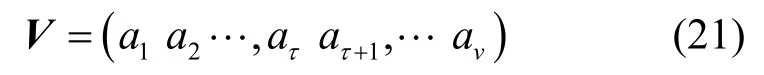
同理，求出u維向量空間的子空間N(M12)的一組基向量{β1,β2,…,βλ}，記λ=rank(N(M12))，再求出的一組基向量則預編矩陣U的列向量如式(22)所示。

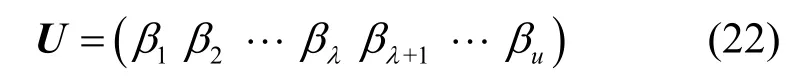
由于U和V的列向量分別由u維向量空間和v維向量空間的基向量構成，從而U和V均為滿秩矩陣。

把U和V分別代入式(19)和式(20)，則式(19)中的分塊矩陣至少有前τ列為全零列，式(20)中的分塊矩陣M12U至少有λ列為全零列。

5 基于干擾消除的網絡編碼優化構造

5.1 二級預編碼策略

本文采用二級預編碼策略，具體如圖3所示，其中，預編碼1用于控制源點的實際發送速率，預編碼2用于消除宿點的干擾。

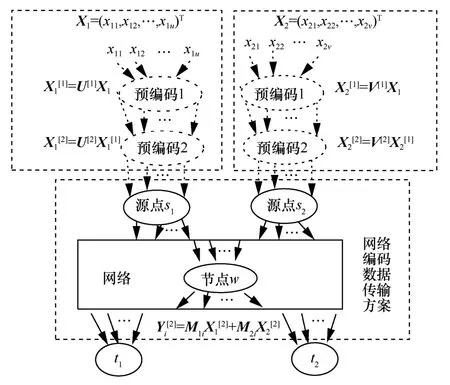
圖3 二級編碼策略示意

源點的數據發送速率假設為(u,v)，選取傳輸方案θ，在此基礎上，在源點實施如式(23)所示的預編碼1。

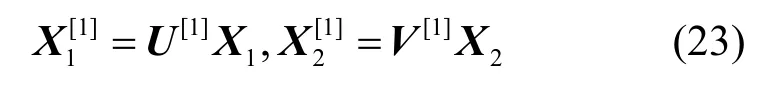
U[1]為u階方陣，如式(24)所示。

V[1]為v階方陣，如式(25)所示。

其中，wi(i=1,2,…,u)和zj(j=1,2,…,v)均為GF(q)中的元素，其值為1或0。

在實施了預編碼1的基礎上，再在源點實施如式(26)所示的預編碼2。

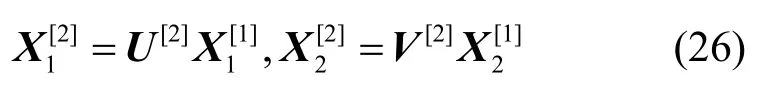
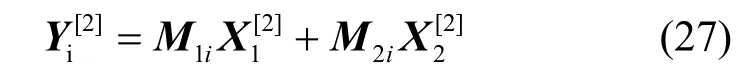
把式(23)和式(26)代入式(27)，則宿點t1和t2得到的線性方程組分別如式(28)和式(29)所示。

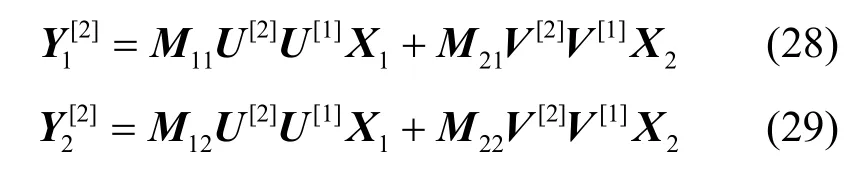
把式(28)寫成如式(30)所示形式。

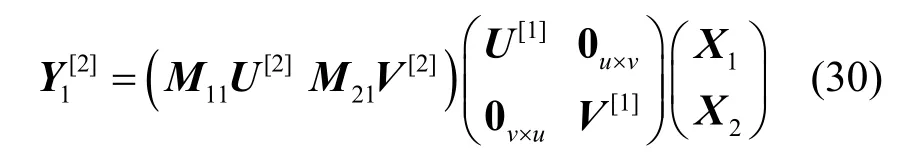
把式(29)寫成如式(31)所示形式。

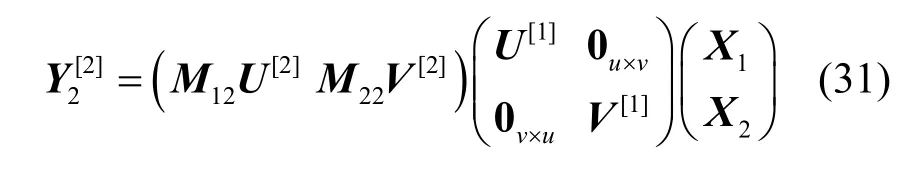
記式(30)的系數矩陣為C，式(31)的系數矩陣為B。

記式(22)所示的列向量為U[2]，式(21)所示的列向量為V[2]，現在來計算和因為V[2]的前τ列是N(M21)的基向量，則分塊矩陣的前τ列必為全零列；同理，分塊矩陣的前λ列必定為全零列。注意到，矩陣C和B均是2個矩陣的乘積，在相乘的2個矩陣中，后者是對角矩陣，因此，根據對角矩陣相乘的特點，若τ≠0，則矩陣C的第u+1,u+2,…,u+τ列必定為全零列；同理，矩陣B的前λ列必定為全零列。

盡管系數矩陣C和B中出現了一些全零列，但不一定能滿足推論1的條件，接下來，通過選取合適的U[1]和V[1]中的對角線元素來增加全零列的數目，使式(30)和式(31)能滿足推論1。

根據矩陣相乘的性質，若wi=0，則矩陣C和B的第i列必定為全零列；若zj=0，則矩陣C和B的第u+j列必定為全零列。

置零規則：在需要置wi（i=1,2,…,u)，zj（j=1,2,…,v）的值為零時，應優先選取下標大者的元素。例如，若需設置wi中的一個元素為0，則應讓下標最大的元素wu為0，其余元素均為1；若需設置wi中的2個元素為0，則應讓下標最大的2個元素wu和wu-1為0，其余元素均為1。

5.2 可達信息率區域邊界點及其相應的傳輸方案

由定理2可知，可達信息率區域內部節點的可行傳輸方案可以由邊界點的可行傳輸方案導出。為了減少計算量，只需要找出可達信息率區域的邊界點，并保存相應的網絡編碼數據傳輸方案。

可達信息率區域邊界點集合的定義具體如下。

設P為可達信息率區域，Q為可達信息率區域的邊界點形成的集合，R為可達信息率區域內部點形成的集合。R的定義如下：?(u1,v1)∈R，則?(u2,v2)∈P，有(u2,v2)控 制 (u1,v1)，即(u1,v1)?(u2,v2)，且(u1,v1) ≠ (u2,v2)。則Q=P-R就是邊界點形成的集合。

為了保存邊界點的傳輸方案，現定義一個二元組<(x,y),θ>，其中第一個元素是邊界點的二維坐標，第二個元素是這個邊界點所依賴的傳輸方案。記這些二元組形成的集合為Q′，其定義為Q′={<(x,y),θ>:(x,y)∈Q}。求邊界點集合Q′的遞歸算法如算法1所示。

5.3 傳輸方案的優化

本文采用隨機線性網絡編碼方法得到傳輸方案θ，則能唯一地確定(M11M21)和(M12M22)，進而唯一確定從而它們的全零列的列數τ和λ可唯一確定，因此，τ和λ是θ的函數，分別記為τ(θ)、λ(θ)。當τ(θ)和λ(θ)的值較大時，則在預編碼1中只需讓wi、zi中較少項置0，就能使式(30)和式(31)滿足推論1，則源點的實際發送速率較大。因此，需要尋找較優的傳輸方案θ，使τ(θ)和λ(θ)的值盡可能大，這是一個雙目標優化問題。

記Ω為所有傳輸方案的集合，則該雙目標優化問題描述如式(32)所示。

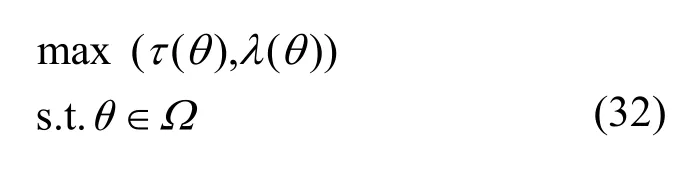
式(32)所示的雙目標優化問題可以通過多目標進化算法來求解。文獻[21-22]運用多目標進化算法求最優的網絡傳輸方案的近似解，也可以采用蒙特卡羅法來求式(32)的近似最優解。本文采用文獻[22]類似的方法，運用了相同的遺傳表示，只是適應度函數與文獻[22]不相同，求出的最優解是一個Pareto邊界。

5.4 算法描述

算法2雙單播網絡的構造算法

步驟1利用Ford-Fulkerson算法[23]，分別求雙單播網絡的k1-1、k2-2、k12-1、k12-2。令u=k1-1、v=k2-2，針對源點的數據發送速率向量(u,v)，運用類似文獻[22]的方法求出式(32)的近似最優解，記為Γ。

步驟2選定近似最優解中的一個傳輸方案θ∈Γ，并置Γ=Γ-{θ}。則由θ唯一確定M11、M21、M12、M22、U[2]、V[2]、和并得出τ和λ值。

步驟3針對θ，調用算法1。

步驟4判斷Γ是否為空集，若不為空集，則轉到步驟2，否則算法結束。

算法結束后，Q′為可達信息率區域的邊界點及其相應的傳輸方案的二元組形成的集合。下面說明這一事實：若通過算法2求出了Q′，則①通過Q′可以獲得可達信息率區域P；② 對于?(x,y)∈P，可以找出以(x,y)為數據發送速率向量的可行傳輸方案。

首先，由Q′的定義，可以從集合Q′中得到Q，進而獲得R，從而得到P=R∪Q。

對于?(u1,v1)∈Q，必存在<(u1,v1),θ1>∈Q′，其中θ1表示發送速率向量(u1,v1)所依賴的傳輸方案。從算法1的求解過程可知，由傳輸方案θ1可以唯一確定M11、M21、M12、M22，進而唯一確定U[2]和V[2]，由(u1,v1)可以得出在U[1]和V[1]需要置零的項數，再按照置零規則，則矩陣U[1]和V[1]唯一確定，因此，由傳輸方案θ1導出的傳輸方案唯一確定。

對于? (u2,v2)∈R，由R的定義，必定存在(u1,v1)∈Q，滿足(u2,v2)?(u1,v1)，由此可知，(u1,v1)導出傳輸方案唯一確定，再根據定理2，則能夠以(u1,v1)的導出傳輸方案為基礎，在源點再次進行預編碼，導出關于(u2,v2)的可行傳輸方案。由于P=R∪Q，則上述結論成立。

綜上，算法2特別適用于實際應用場景。從算法的結果Q′中不僅能得出可達信息率區域，且對于區域中的每一點，能容易地得到相應的可行傳輸方案。

值得說明的是，由于本文只能求出式(32)的近似最優解，故求出的可達信息率區域也是近似最優的。

6 算例

圖4表示一個雙單播網絡，容易求出k1-1=k1-2=k12-1=k12-2=3。選擇伽羅華域GF(23)，其不可約多項式為x3+x+1，寫成二進制形式為(1011)2。選定源點數據發送率向量為(u,v)=(3,3)，現運用隨機線性網絡編碼方法并結合多目標優化的進化策略來確定較優的傳輸方案，本例只求出了一個傳輸方案，在該傳輸方案下，宿點t1和宿點t2的全局編碼向量形成的矩陣分別如式(33)和式(34)所示。

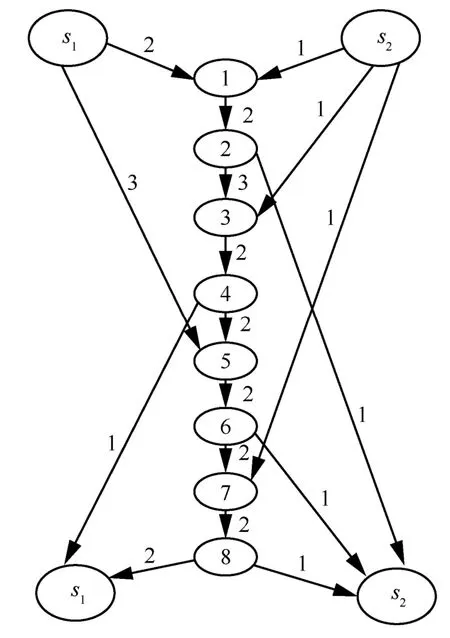
圖4 一個雙單播網絡實例

求出預編碼2的預編碼矩陣，如式(35)所示。

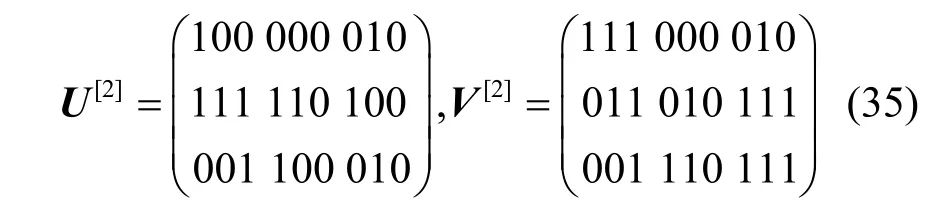
從而可得

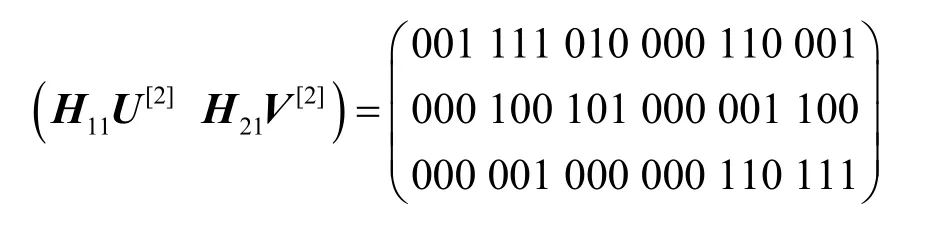
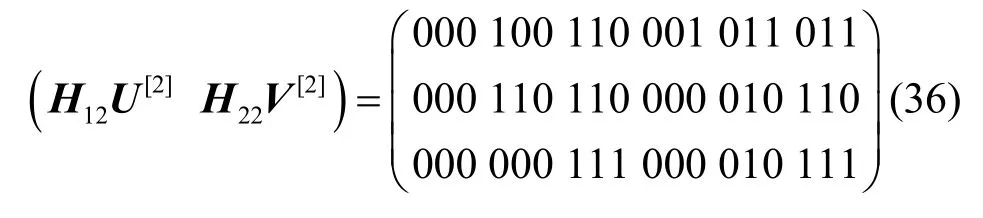
可以看出，無論是宿點t1還是宿點t2，均不能求解線性方程組，因為這2個系數矩陣的非全零列數均為4，而矩陣的秩均為3，所以必須在源點利用預編碼1來控制源點的實際發送速率。

源點實施二級預編碼后，宿點t1得到的線性方程組的系數矩陣為

宿點t2得到的線性方程組的系數矩陣為

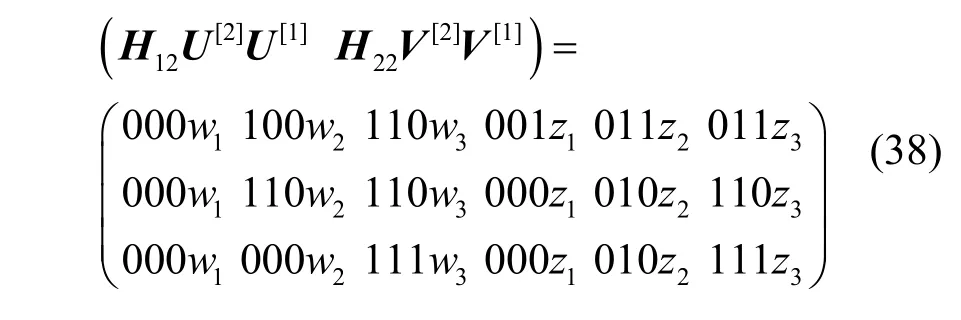
在式(37)和式(38)中，系數矩陣均為3行6列的矩陣，每個矩陣均有1個全零列，要使系數矩陣滿足推論1的條件，至少還要讓每個矩陣的另外2列為全零列，則必須讓wi和zi（i=1,2,3）中的其中2項置零，根據置零規則，有以下3種置零方式，具體如下。

1)w1=1，w2=w3=0，zi=1（i=1,2,3）。

2)z1=1，z2=z3=0，wi=1（i=1,2,3）。

3)w1=w2=1，w3=0，z1=z2=1，z3=0。

從而得到預編碼1的3組矩陣，如式(39)所示。

它們對應的實際發送速率向量分別為(1,3)、(3,1)、(2,2)。

現分析第3種情況，其余2種情況類似。因實際的發送速率向量為(2,2)，在一次數據傳輸中，假設源點s1傳輸的字符向量為X1=(111,110,?)*為了所提的方法具有統一性，盡管實際上只發送2個字符，但采用發送3個字符的格式，最后一個字符沒有傳輸至網絡，因此，該字符的選取隨意，本文用“?”表示。，源點s2傳輸的字符向量為X2=(100,010,?)，則源點s1的預編碼矩陣為

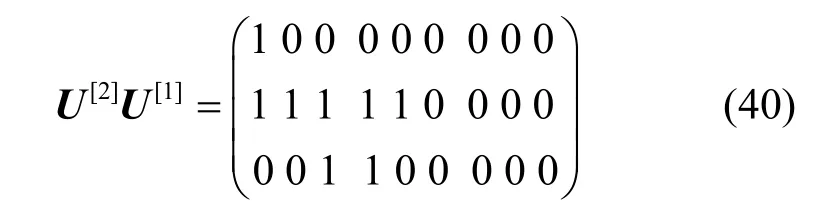
經預編碼后得到的字符向量為

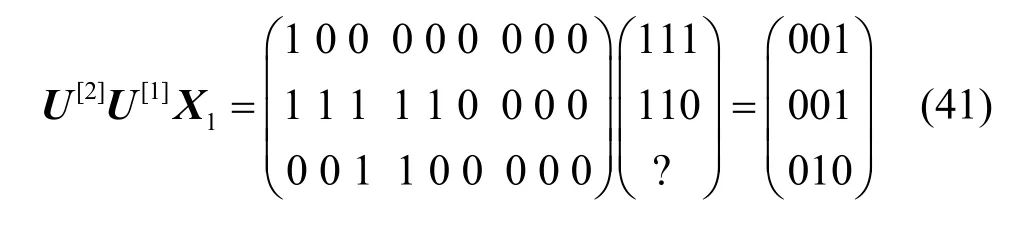
源點s2的預編碼矩陣為

源點經預編碼后，分別把預編碼矩陣對應的全局編碼向量和預編碼后的字符采用已定的網絡編碼數據傳輸方案進行傳輸。則宿點t1把得到的全局編碼矩陣和接收到的字符進行聯立形成線性方程組，如式(44)所示。

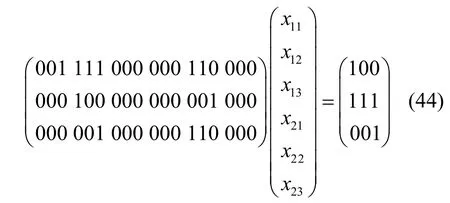
宿點t2把得到的全局編碼矩陣和接收到的字符進行聯立形成線性方程組，如式(45)所示。

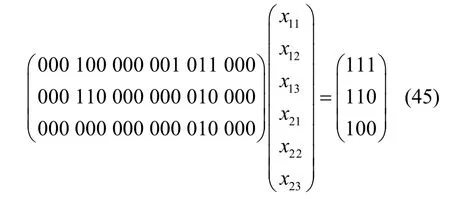
式(44)和式(45)顯然滿足推論1的條件，從而可以求解。式(44)可以解出x11、x12、x22，其結果為(x11,x12,x22)=(111,110,010)；式(45)可以解出x12、x21、x22，其結果為(x12,x21,x22)=(110,100,010)。

綜上，宿點t1能解碼出源點s1的2個字符，宿點t2能解碼出源點s2的2個字符，即源點的發送率向量為(2,2)。

其他2種情況可以類似地進行討論。

綜合這3種情況，可以得到源點的可達信息率區域，如圖5所示，其中，橫坐標的單位是字符/單位時間。

圖5 雙單播網絡的可達信息率區域

以上給出了可達信息率區域邊界點的網絡編碼數據傳輸方案，對于可達信息率區域的坐標為整數的內部點，由定理2可知，可以從邊界點的網絡編碼數據傳輸方案中導出。例如，對于坐標為(2,1)的點，可以從邊界點(2,2)或(3,1)的網絡編碼數據傳輸方案中導出。

7 結束語

本文提出了一種雙單播網絡編碼的構造方法，采用源點預編碼技術，中間節點采用隨機線性網絡編碼技術，并結合多目標優化進化策略來確定傳輸方案，利用源點至宿點的信息轉換矩陣的零向量空間的基向量和行向量空間的基向量共同來確定源點的預編碼矩陣的列向量，實現了在宿點消除信息干擾的目標。由雙單播情形下的網絡編碼導出技術，提出了二級預編碼策略來控制源點的發送速率，從而能夠得到可行的網絡傳輸方案。由多目標進化策略，可以求出雙單播網絡編碼的近似的可達信息率區域的邊界點及相應的可行傳輸方案。本文還論證了如下結論：只需要求出可達信息率區域邊界點的可行傳輸方案，內部點的傳輸方案可以從相應邊界點的傳輸方案中導出。因此，所提方法不僅可以求出雙單播網絡編碼的近似可達信息率區域，還為求出的可達信息率區域的每一個整數坐標點提供了構造可行傳輸方案的方法，適合于網絡編碼技術的實際應用。

多單播網絡是一個比較困難的問題，能否把這一方法推廣到三單播網絡乃至源點數更多的多單播網絡，將是下一步需要進行的研究工作。