基于Stackelberg博弈的雙目標WOA頻譜共享算法

張力，廖天，何業軍

（深圳大學電子與信息工程學院，廣東 深圳 518060）

1 引言

人們對通信的需求從早期的文字通信演變為當今的視頻通信[1]。隨著通信需求的不斷增加，有限的頻譜資源很難滿足人們的需求[2]，主要表現為現有頻譜資源調度和分配的不合理[3]。

現有的頻譜資源共享方式[4]無法最大程度地保證通信服務質量，原因是在解決認知用戶和授權用戶之間頻譜資源的共享問題及認知用戶之間頻譜資源的競爭問題時沒有考慮授權用戶和認知用戶的通信質量，也沒有考慮系統中所有用戶的公平度，對于系統中授權用戶和認知用戶之間的競爭也沒有考慮。而解決這類問題的主要方法就是博弈論[5]，通過博弈論的相關原理有效地解決授權用戶和認知用戶之間的競爭關系，使最終的調度方案達到納什均衡[6]。

Niyato等[7]對合作博弈方式和非合作博弈方式進行了對比分析，對這2種博弈方式的應用場合、優缺點及構架進行了介紹，并給出了不同場合選擇博弈方式的依據，為博弈論的進一步應用奠定了基礎，但只停留在理論分析階段。Kim 等[8]提出了一種多主多從結構的Stackelberg博弈理論，并從理論上論證了該方法通過多次迭代和反饋之后可以搜索到最優的納什均衡，但復雜的反饋決策限制了應用。Nguyen等[9]提出一種基于預測和感知的頻譜共享方法，該方法將資源塊的時間結構分為頻譜預測、頻譜感知和數據傳輸，改善了部分性能但未在博弈理論進一步研究。Zhu等[10]針對宏用戶提供更多訪問頻譜的機會，設計了一種激勵機制，該機制使用一種分層的動態博弈框架，下層建立演化博弈模型，上層建立Stackelberg差分博弈模型，然而該分層博弈架構將引入層間干擾問題，但文中并未考慮。張婷等[11]設計演化博弈算子，建立分式規劃機制的次用戶效用函數，實現了能效最優的資源分配，但該方法僅考慮能效而未考慮如頻譜利用率等問題。Vidal等[12]基于博弈論研究在不干擾主用戶的條件下讓次用戶使用頻譜，而該方法提高的頻譜利用率有限。Yang等[13]基于Stackelberg博弈調整使資源分配最大化效用，降低能耗，該方法在其他資源分配模型中有待進一步驗證。Al-Talabani等[14]研究基于Stackelberg博弈讓主網絡和次節點共享頻譜資源，并加入噪聲提高認知無線電網絡傳輸保密性。韓松等[15]考慮主用戶二次邊際成本，設計主用戶反饋機制和次用戶信任機制，以最大化效用和提高頻譜利用率，其考慮的主次用戶效用函數較為簡單。博弈和非博弈集中調度最主要的差異是博弈集中調度的認知用戶和授權用戶的博弈結果會相互影響，從而不斷在博弈策略中選擇較優的博弈結果，非博弈集中調度取決于具體的調度參與者，一般不會相互影響。

本文考慮用戶的公平度，給出了反映認知用戶頻譜需求的效益函數，引入了雙目標鯨魚優化算法（WOA,whale optimization algorithm），實現公平有效的頻譜分配。本文的貢獻如下：1)基于Stackelberg博弈引入雙目標WOA，將授權用戶和認知用戶共同的收益優化分為各自的收益優化過程，設計出一種新的基于Stackelberg博弈的頻譜共享調度算法；2)通過加入影響認知用戶公平分配頻譜的函數到認知用戶收益的優化模型中，能實現認知用戶較為公平的頻譜分配，最終得到授權用戶和認知用戶的最優頻譜分配結果。

本文首先描述雙目標WOA；然后建立頻譜共享博弈模型，提出了雙目標WOA頻譜共享算法，并介紹了算法的實現步驟和流程；最后對本文算法進行仿真驗證，分析了算法復雜度、仿真時間、系統效用方面等性能。

2 雙目標WOA

傳統的WOA[16]主要針對單一目標的獵捕，當考慮2個目標獵物時，主要會涉及以下關鍵因素。

1)每個“獵物群”的“獵物”數量。如果2個“獵物群”中的“獵物”個體數量差異比較大，“獵物”個體是否優先考慮大“獵物群”，以滿足“獵物”個體最后的“捕食”需求。

2)距離2個獵物群中心位置的距離。如果“獵物”個體與小數量獵物群的距離遠小于與大數量獵物群的距離，是否先考慮捕食小“獵物群”，進而圍捕大“獵物群”。

3)約束條件。在何種情況下會形成雙目標捕食環境等。

2.1 初始條件

針對初始鯨魚群個體環繞數量，設置個體數量浮動因子F，群族個體數量Q，環繞“獵物”（“獵物1”和“獵物2”）的初始個體數量表示為

其中，rand()表示(0,1)之間的隨機量，Q1與Q2分別表示“獵物1”與“獵物2”初始環繞的捕獵者數量，F表示(0,1)之間的變量。

2.2 距離與權重

距離是優先考慮的因素，當距離優勢足夠明顯時，即d1＞2d2，則不考慮其他因素的影響直接追擊“獵物2”，反之亦然，其中d1和d2表示捕獵者分別與“獵物1”“獵物2”的距離。當距離優勢不夠明顯時，則需要考慮目標對于個體的最要性來決定下一時刻的追擊目標，可得式(3)。

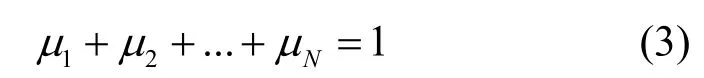
其中，μi表示獵物個體在整個獵物群體中的權值，i=1,2,…,N。當同時考慮距離與權重時，則每個個體在更新位置前需要做出式(4)所示的判斷。

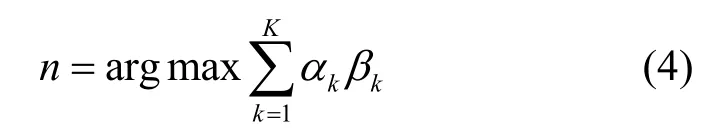
其中，K表示影響目標選擇的個數；αk表示各影響因素之間的比重；βk為對應因素的權值；n表示該時刻捕獵的目標，以對下一時刻的位置進行更新。

2.3 收斂速度與精度

在鯨魚螺旋捕食階段[16]，根據式(5)進行優化。

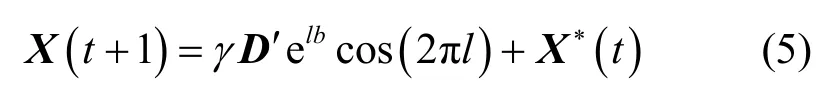
其中，X(t+1)為捕獵者的位置向量；t為迭代參數；D′為捕獵者與獵物的距離向量；l為 0～1的隨機變量；b為常量；X*(t)為每次迭代捕獵者的局部最優位置向量；γ為更新權值，如式(6)所示。

其中，γmin表示最小權值，取值為0.05；γmax表示最大權值，取值為0.95；f(x)表示修正函數，如式(7)所示。

其中，μ表示xi的均值。

2.4 停止條件

選擇狩獵目標數量比和單目標權重比的關系為停止條件，對收斂速率和收斂精度都有一定影響。當滿足式(8)時，停止對于狩獵目標的選擇，以前一時刻的目標為基準，直至完成狩獵目標的捕獲。

其中，Q1(t)和Q2(t)分別表示t次迭代時，環繞“獵物1”與“獵物2”鯨魚的數量。

3 頻譜共享博弈模型

當分布式天線系統（DAS,distributed antenna system）和集中式天線系統（CAS,centralized antenna system）通信過程產生相同的吞吐量時，CAS需要更大的發送功率。當DAS和CAS以相同的發送功率進行通信的時候，DAS具有更高的吞吐量[17]。

DAS和CAS能量效率和頻譜效率的關系如圖1所示。從圖1可知，CAS和DAS在頻率效率小于2 bit/(s.Hz)時，隨著頻率效率的增加，兩者的能量效率均增加。當頻率效率大于2 bit/(s.Hz)時，兩者的能量效率逐漸降低并趨于平穩。由于其天線距離用戶較遠，CAS的大尺度衰落現象較為嚴重，因此能量效率較低。由于DAS的天線隨機分布在小區的不同位置，天線距離用戶較近，因此大尺度衰落現象較輕，能量效率較高。由圖1還可知，DAS的理論最小值的能量效率也大于CAS，因此本文在DAS的基礎上進行研究。

圖1 DAS與CAS能量效率與頻譜效率關系

本文頻譜共享的認知無線電系統如圖2所示。假設系統有M個授權用戶，一個基站及N個隨機分布的天線，其中，N個天線只用于數據信號的發送和接收。所有授權用戶將閑置的頻譜資源整合為一個共享池，并出售頻譜資源給認知用戶，從而獲得收益。認知用戶通過購買共享池的頻譜資源來實現信號發送和接收。基站在整個交易環節作為“中間人”，協調授權用戶和認知用戶間的交易。

圖2 網絡頻譜共享系統

3.1 認知用戶的收益建模

假設授權用戶的價格策略為P*，認知用戶購買的帶寬b*，引入式(9)所示的認知用戶收益函數[18]。

其中，U(b)為認知用戶的收益；b=[b1,...,bi,...,bM]表示M個授權用戶給基站的帶寬向量；表示認知用戶的頻譜利用率；ωi表示認知用戶所擁有的單位傳輸速率下所帶來的收益；Pi表示授權用戶i的頻譜價格；b′j表示認知用戶j的實際頻譜需求；f(·)表示實際的頻譜需求函數，其作用是當實際的網絡頻譜需求改變時，認知用戶收益也會改變，所得的均衡點也會發生改變[19-20]，從而使認知用戶收益更符合實際頻譜需求情況。

假設xij表示天線j的頻譜資源是否分配給用戶i，如果是，則xij=1，否則xij=0。那么認知用戶的收益目標函數為

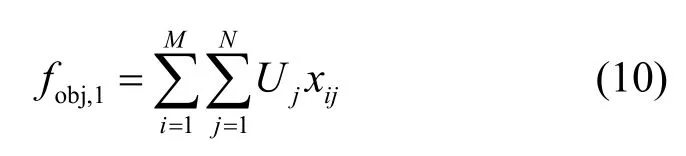
其中，Uj表示認知用戶的收益函數，即式(9)的認知用戶收益函數。如果某個用戶i被分配天線j，那么將產生一個收益Uj。然后通過式(10)計算得到所有認知用戶的整體收益值。

3.2 授權用戶的收益建模

單個授權用戶的收益函數為[21]

其中，Mi表示授權用戶的連接數量；c1表示授權用戶收益權值；c2表示授權用戶損失權值；表示授權用戶系統連接者需求帶寬；表示授權用戶的頻譜利用率；Wi表示授權用戶擁有的閑置頻譜資源。

當存在多個授權用戶時，授權用戶的收益函數將有所不同。在Stackelberg博弈中，假設授權用戶A的頻譜資源價格為pA，授權用戶B觀測到A的價格后，考慮自身的利益，選擇價格pB。在整個過程中，A先有價格，B根據A的價格選擇價格，而A無法預先獲得B的價格。B的策略定義為SB:QA→QB，其中，QA=(0,∞)表示A的價格區間，QB=(0,∞)表示B的價格區間。因此，其價格向量可以表示為(pA,SB(pA))。同理，對于授權用戶C，其價格向量表示為(pA,pB,SC(pA,pB))，其中，pB=SB(pA)。在Stackelberg博弈中，本文以2個授權用戶為例，則授權用戶收益函數為[21]

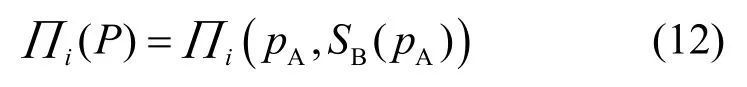
那么授權用戶的收益目標函數為

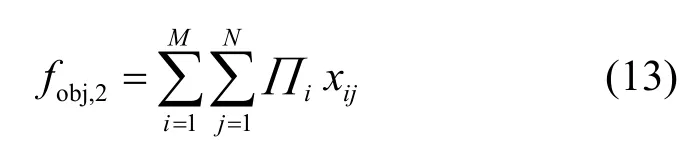
其中，Пi(P)為授權用戶的收益函數，即式(12)的授權用戶收益函數。如果天線j的頻譜資源被出售，那么對授權用戶將產生一個收益Пi。通過式(13)計算得到所有授權用戶的整體收益值。

3.3 認知用戶公平度建模

頻譜分配的公平度目標函數如式(14)所示。

其中，ξ表示一個較小值，一般取0.000 01，以避免出現值為0的情況。

假設某一天線的閑置頻譜資源較多，其他天線閑置頻譜資源較少，若大多數用戶都去搶占該天線資源，將會導致認知用戶的個體收益下降，而采用頻譜分配的公平度目標函數后，認知用戶則選擇不同的天線來均衡地購買頻譜資源。

3.4 系統效用的建模

認知用戶和授權用戶的整體收益反映系統效用，設認知用戶和授權用戶收益歸一化值分別為y1和y2，系統效用函數為

其中，λ1和λ2表示加權值，均取值0.5。

3.5 雙目標WOA頻譜共享算法

在Stackelberg博弈的基礎下，本文所采用雙目標WOA頻譜共享算法的優化模型如式(16)和式(17)所示。

其中，δ1、δ2和δ3表示權值，有δ1+δ2+δ3=1。如果頻譜分配結果偏向于認知用戶收益，增大δ1；如果頻譜分配結果偏向于授權用戶收益，增大δ2；如果頻譜分配結果偏向于認知用戶的公平度，則增大δ3的值。

在優化模型中，為了避免出現不符合實際情況的最優解，使頻譜分配更符合實際情況，設置了3個約束條件[17]，如式(18)～式(20)所示。其中，式(18)表示所有認知用戶的整體頻譜資源需求之和小于所有授權用戶的閑置頻譜資源；式(19)表示每一個用戶只使用某一個授權用戶的頻譜資源或者不使用任何授權用戶的頻譜資源；式(20)表示如果認知用戶被分配某授權用戶的頻譜資源，那么xij={1}，否則xij={0}。在該約束條件下的優化結果中，優化模型的結果將更符合實際頻譜需求。

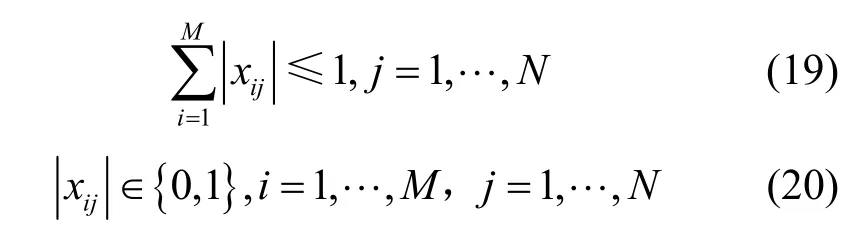
3.6 算法步驟及流程

在雙目標WOA頻譜共享算法中，需要優化變量xij的值，所有的xij可組合成M×N維向量，將其轉換為一維向量記為

那么在雙目標WOA頻譜共享算法中，只需要將待優化變量[x11,...,x1N,x21,...,x2N,...,xM1,...,xMN]、式(16)和式(17)的優化目標加入算法進行優化即可。具體步驟如下。

Step1進行參數初始化，隨機分配參數[x11,...,x1N,x21,...,x2N,...,xM1,...,xMN]，即在初始條件下，認知用戶隨機分配頻譜資源。

Step2根據式(16)和式(17)計算初始參數下認知用戶的優化目標和授權用戶的優化目標。

Step3開始進入雙目標WOA優化，結合第2節，通過WOA的鯨魚行走覓食階段、鯨魚包圍階段和鯨魚螺旋捕食階段實現參數[x11,...,x1N,x21,...,x2N,...,xM1,...,xMN]的迭代更新，并同時計算對應的優化目標函數值。

Step4將每次迭代計算得到的優化目標函數值和當前迭代的最優目標函數值進行對比，并獲得較優的目標函數值。

Step5重復上述步驟，直到完成所有的迭代計算，將最后迭代輸出的參數[x11,...,x1N,x21,...,x2N,...,xM1,...,xMN]作為最后的優化結果，即頻譜分配結果。

雙目標WOA頻譜共享算法流程如圖3所示。

圖3 雙目標WOA頻譜共享算法流程

4 性能測試與分析

仿真實驗參數如表1所示。本文算法將與基于Bertrand博弈算法和基于Stackelberg博弈算法進行對比仿真，其中，基于Bertrand博弈算法無法反映實際的頻譜需求，屬于靜態博弈；基于Stackelberg博弈算法可以反映實際的頻譜需求，屬于動態博弈。通過與這2種博弈進行對比，可討論不同博弈對仿真性能的影響。

表1 仿真實驗參數

價格納什均衡點和頻譜請求帶寬納什均衡點的仿真結果如圖4和圖5所示，這2個均衡點是與性能相關的分技術指標。由圖4可知，2個授權用戶的價格呈正向變動，這意味著當一個授權用戶提高價格時，另一個授權用戶也會提高價格，其反應函數曲線呈y=x對稱形式。圖4中，P1和P2表示授權用戶1和授權用戶2的歸一化價格。由圖5可知，2個認知用戶的頻譜請求帶寬與授權用戶價格呈反比，即授權用戶價格越低，請求帶寬越高。認知用戶的請求帶寬提高會降低授權用戶的頻譜價格，間接提高授權用戶出租的頻譜資源，從而提高認知用戶和授權用戶的收益，進一步提高系統效用，而系統效用的提升也意味著通信系統的吞吐率的提升。由圖4和圖5可知，基于Stackelberg博弈算法相對于基于Bertrand博弈算法，其頻譜價格有一定程度的降低，而認知用戶的頻譜請求則較大幅度提升。而本文算法中，各授權用戶在參考其他授權用戶的價格后才給出價格，因此其最終的價格將低于基于Stackelberg博弈算法的博弈模型，而其對應的認知用戶頻譜請求則最大。

圖4 授權用戶的價格納什均衡點

最佳授權價格隨可出租的閑置頻譜資源增加而變化的仿真結果如圖6所示，最佳授權價格是與性能相關的分技術指標。由圖6可知，隨著可出租的閑置頻譜資源的增加，為了讓更多的認知用戶購買頻譜資源，其最優的授權價格逐漸減低。當閑置頻譜資源增加到一定程度時，為保證授權用戶的收益，其授權價格將趨于穩定。其中，基于Bertrand博弈算法考慮的情況較為理想化，認為博弈參與者最優價格最大，從而使認知用戶收益降低。基于Stackelberg博弈算法相對于基于Bertrand博弈算法更符合實際情況，能夠吸引更多的認知用戶來購買頻譜資源，因此得到的最優授權價格低于基于Bertrand博弈算法的價格。本文算法采用了基于Stackelberg博弈算法，各個授權用戶在參考其他授權用戶的價格后才給出價格，最終的價格將低于基于Stackelberg博弈算法，因此具有最低的授權價格。3種算法的最終價格分別為5.95（本文算法）、6.36（基于Stackelberg博弈算法）、7.03（基于Bertrand博弈算法）。本文算法的最終價格為基于Bertrand博弈算法價格的84.64%，為基于Stackelberg博弈算法價格的93.55%。

圖6 授權頻譜最佳授權價格變化

授權用戶收益隨著可出租的閑置頻譜資源增加而變化的仿真結果如圖7所示，授權用戶收益是與性能相關的分技術指標。由圖7可知，隨著可出租閑置頻譜資源的增加，授權用戶的收益逐漸增加，這是由于當閑置頻譜資源逐漸增加，其售價不斷減低，從而吸引更多的認知用戶購買頻譜資源。當閑置頻譜資源大于5的時候，隨著認知用戶的頻譜需求逐漸得到滿足，授權用戶出售的頻譜價格逐漸趨于穩定，系統的整體收益也逐漸平穩。同理，由于基于Bertrand博弈算法假設博弈參與者的條件是完全相同的，在實際的系統中的最優價格最大，導致參與購買頻譜資源的認知用戶較少，因此整體的收益最低。基于Stackelberg博弈算法的頻譜價格小于基于Bertrand博弈算法，因此整體收益更高。本文算法采用了基于Stackelberg博弈，價格最低，參與購買的用戶數量也最多，因此整體收益也最大。3種算法對應的授權用戶的最終收益分別為455（本文算法）、364（基于Bertrand博弈算法）、418（基于Stackelberg博弈算法）。本文算法授權用戶的收益相對于Bertrand博弈算法價格提升了25%，相對于基于Stackelberg博弈算法價格提升了8.85%。

認知用戶收益隨著可出租的閑置頻譜資源增加而變化的仿真結果如圖8所示，認知用戶收益是與性能相關的分技術指標。由圖8可知，隨著可出租的閑置頻譜資源的增加，認知用戶的收益逐漸增加，由于頻譜資源價格的不斷降低，對于購買者認知用戶來講，其收益逐漸增加，當閑置資源數量大于20時，絕大多數認知用戶的頻譜需求得到了滿足，授權用戶出售的頻譜價格也趨于穩定，因此其收益保持不變。由于基于Bertrand博弈算法假設博弈參與者的條件是完全相同的，因此該算法應用到實際的系統中，其最優價格最大，認知用戶的收益自然也就最小。而基于Stackelberg博弈算法，其頻譜價格小于基于Bertrand博弈算法，認知用戶的收益較高。而本文算法的價格最低，認知用戶的收益也最大。3種算法對應的認知用戶的最終收益分別為2 789（本文算法）、2 563（基于Bertrand博弈算法）、2 307（基于Stackelberg博弈算法）。本文算法中認知用戶的收益相對于基于Bertrand博弈算法價格提升了20.89%，相對于基于Stackelberg博弈算法價格提升了8.82%。

圖7 授權用戶收益

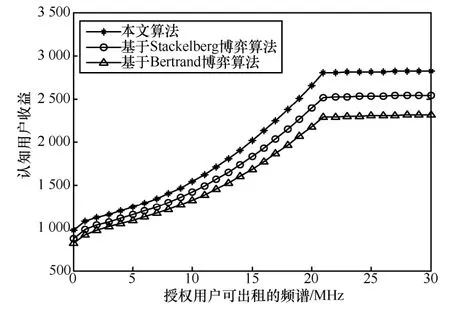
圖8 認知用戶收益

系統效用是系統的技術指標，系統效用隨用戶數量的變化情況如圖9所示。由圖9可見，隨著用戶數量的逐漸增加，不同博弈模型下的系統效用均逐漸增加。若都不考慮認知用戶公平度，基于Bertrand博弈算法及基于Stackelberg博弈算法的系統效用均比本文算法低，這是由于仿生智能算法具有強并行計算能力，經過復雜的迭代優化獲得了較優授權用戶受益和認知用戶受益，因此其系統效用將會更高。

圖9 系統效用

圖10給出了不同公平加權系數δ3對算法性能的影響，分別設置δ3=0.9、δ3=0.5、δ3=0.1。公平度是通信性能的技術指標，它和通信網絡的業務吞吐率是相互矛盾的，如果公平度越高，通信網絡的業務吞吐率將會越低，如果公平度越低，通信網絡的業務吞吐率將會越高。由圖10可知，對比3種算法的系統效用，當公平度加權系數較小的時候，頻譜資源分配受認知用戶信道質量影響較小，本文算法可以獲得更高的系統效用，而當公平度加權系數較大的時候，由于算法過于強調公平度，信道較差的認知用戶也能獲得較多頻譜資源，反而影響了最終的系統效用。因此，在實際中，需要根據用戶的實際需求來設置加權系數。

圖10 不同公平加權系數δ3對系統效用的影響

圖11給出了對200個用戶使用3種對比算法其對應的公平度指標，此時由圖11可知，由于本文算法在頻譜分配過程中，考慮了頻譜分配公平度指標，因此進行頻譜分配時具有最高的公平度，平均達到了86.8%。而基于Stackelberg博弈算法雖然考慮了實際博弈過程的特點，但是由于沒有涉及公平度的因素，其最終分配結果所計算得到的公平度只有71.3%。基于Bertrand博弈算法假設了各個博弈參與者完全相同的條件，因此在實際中，無法獲得較好的頻譜分配結果，其公平度只有59.2%。

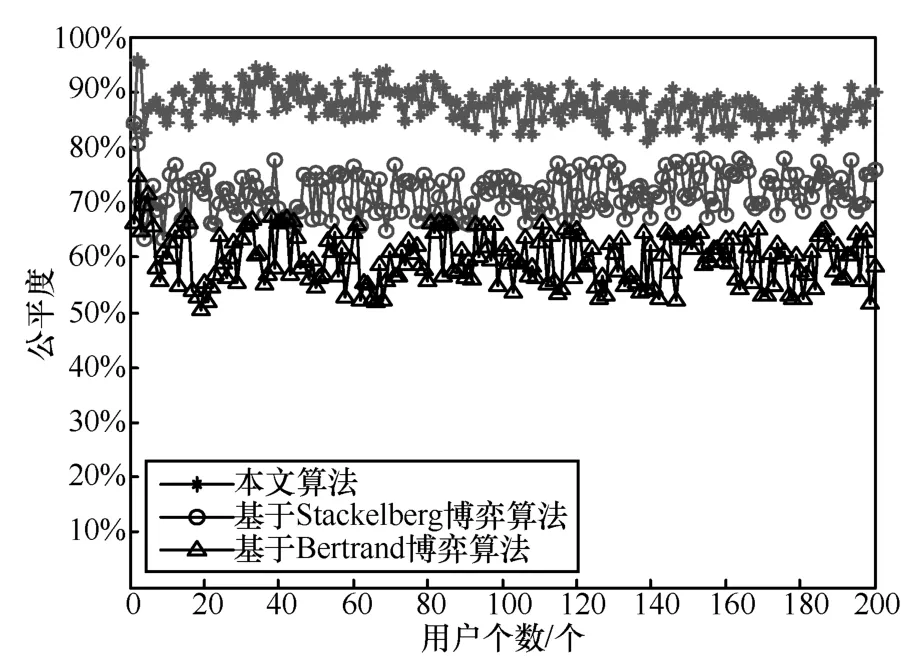
圖11 系統公平度指標對比

圖12給出了3種對比算法對應的仿真時間，其是與通信相關的分技術指標，對認知用戶數量從10逐漸遞增到200的仿真時間進行對比。由圖12可知，本文算法的仿真時間最長，因為通過雙目標WOA優化需要迭代，這會增加算法的復雜度。而基于Bertrand博弈算法的實現復雜度最小，因此其仿真時間最短。

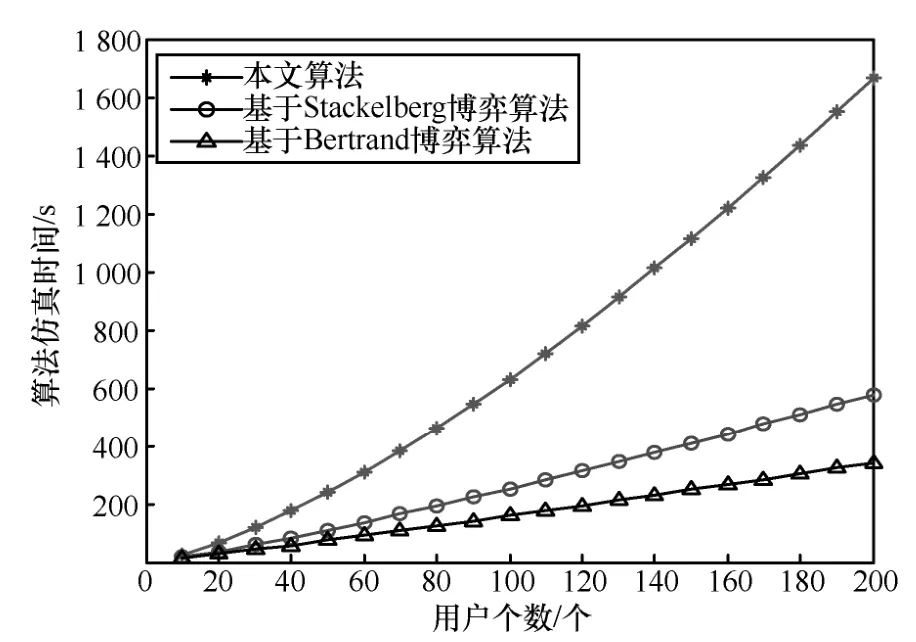
圖12 算法仿真時間對比

通過以上分析，在考慮公平度的情況下，本文算法的復雜度和仿真時間雖然不占優勢，但其他性能優勢明顯，故本文算法在整體上有較為明顯的性能優勢。

5 結束語

通過分析WOA的特點及應用對象，提出了一種雙目標WOA頻譜共享算法，并給出了算法步驟和流程。本文基于Stackelberg博弈，引入強并行計算能力的雙目標WOA，加入影響認知用戶公平分配的函數，建立基于Stackelberg博弈的雙目標WOA頻譜共享算法。仿真結果符合預期目標，在算法復雜度、仿真時間和系統效用方面性能雖稍占劣勢，但其他性能均取得較好結果，因此，所提方法在博弈論的頻譜共享中有一定探索價值。