基于改進的格子氣模型的人員疏散模擬研究

賈麗

（重慶城市管理職業學院智能工程學院，重慶401331）

0 引言

根據《2018 年國民經濟和社會發展統計公報》，隨著我國城市化進程的不斷發展，目前城鎮化率已經接近60%，并且還在快速提高之中，城市人口會越來越多，公共場所人群也越來越密集，特別是近幾年出現的網紅打卡點（如重慶朝天門、解放碑、洪崖洞等）都是呈現出地方小、人員多的特點，極易發生人員踩踏等安全事故，造成生命財產重大損失。如何在緊急情況下對密集人群進行安全有效的疏散是公共安全領域的一個重要研究項目。行人疏散動力學研究利于高效、安全以及舒適的行人交通設計和大規模人群管理。

行人流研究目前最有效的方法就是數值仿真模擬，常用的動力學模型有Hughes 等人的流體動力學模型[1-2]，Hoogendoom 和 Bovy 等人的氣體運動學模型[3]，這兩種模型是宏觀和介觀模型。微觀模型有Helbing等基于牛頓第二定律提出的社會力模型[4]和Muramatsu等人提出的格子氣模型[5-8]等。這些模型都能從某一個方面模擬行人流的一些特征，尤其微觀模型能夠較精確再現個體之間的相互作用[9-11]。本文在無后退偏隨機行走格子氣模型基礎上進行了修改，使其更加符合行人疏散實際特點，利用修改后模型研究了緊急情況下單出口室內人員疏散的規律。

1 改進的格子氣模型

基于實際行人疏散特點的分析，對無后退偏隨機行走格子氣模型作了如下修改：

首先漂移系數D的組成除了考慮離出口距離遠近因素外，還考慮了實際問題中擁擠人群偏向中間位置逃生速度要大于邊緣位置這一因素，所以：

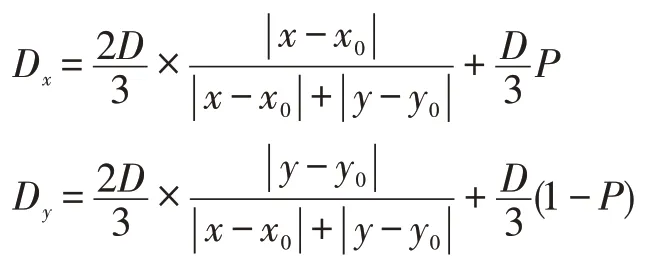
其中P：向中間位置移動的偏向因子。

其次偏隨機行走格子氣模型一般采用順序更新，考慮實際疏散情況，顯然采用并行更新更加合理一些。并行更新中多者競爭同一空位，每一位競爭者獲得此空位概率并不相同，而是與此競爭者向此空位移動的愿望強烈程度成正比。所以對空位競爭我們采用不同的策略。以室內中間左側空間為例來說明策略，中間位置和中間位置右側空間情況與此類似。

對于一個空位來說，它共有8 種情形，如圖1所示。

對于（a）情況：

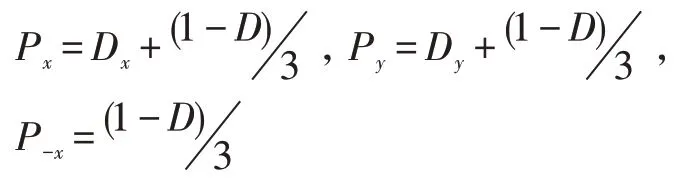
對于（b）情況：

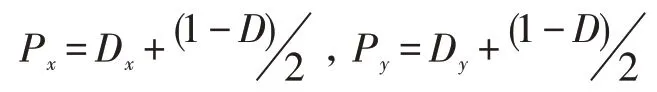
對于（c）情況：

對于（d）情況：

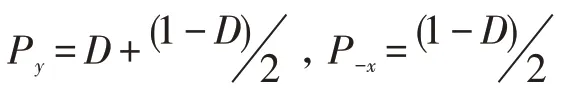
對于（e）、（f）、（g）情況：

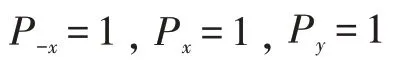
對于（h）情況：沒有人員要移動到此，什么都不做。

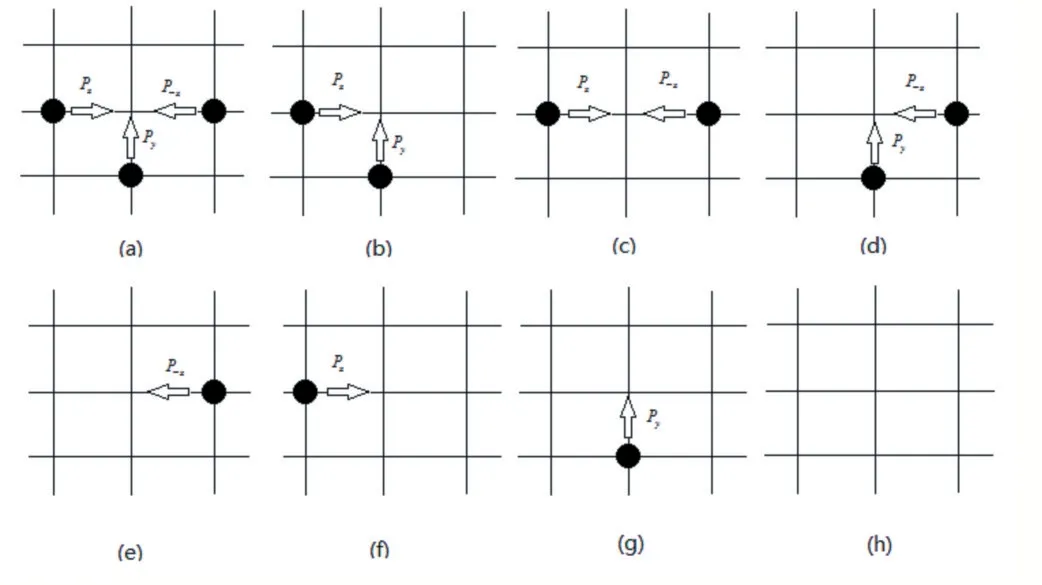
圖1 不同空位競爭情形圖

2 室內人員疏散參數及其模擬計算

室內空間用200×200 正方形網格替代，每個1×1的正方形小方格邊長相當于一個成年人的平均體寬，人只能處在格點上，一個格點上只允許有一個人。出口在中間位置，出口的寬度為5（即可以同時讓5 個人進出）。我們設定初始狀態人員密度為0.3（即室內30%的格點上有人），并且人員隨機分布在不同格點上。下個時間步，所有人員開始向出口位置移動。我們假定出口外面是一個很大的空間，人員從出口出來后可以很快散開，不會對內部人員疏散造成影響，所以人員一旦從出口出去便會被移去。所有人員從室內出來后疏散結束，所用的總時間步數作為疏散時間。

圖2 不同時間步室內人員位置圖

圖2 是模擬計算得到的不同時間步室內人員位置圖。從圖上可看出擁堵的形成過程和典型的拱形擁堵。在緊急情況下擁擠人群會產生“越快越慢”的現象，人們都加速向出口移動，使得出口位置的擁堵過早形成，反而增加了疏散時間，這和實際情況相符合。從圖（c）-（f）上還可以看到拱形擁堵不對稱消失，結果圖顯示拱形擁堵形成以后，人群中存在一個通道，此通道往往可以使周圍人員快速疏散出去，通道位置如果不在出口正中央，就會造成拱形擁堵一邊的疏散速度要大于另一邊，造成拱形擁堵形狀上的對稱性被破壞。這就是說疏散越快的地方越快，越慢的地方越慢。而這種情況也是和現實相符合，是合理的結果。

我們計算了疏散平均速度隨時間步的關系。每一個時間步的平均速度v定義為：每一個時間步移動的粒子數占系統中存在的總粒子數的比率。一個時間步T定義為：所有人員嘗試移動一次為一個時間步。

圖3 平均速度隨時間步變化關系

從圖3 可看出，起始階段人員活躍度較高，平均速度v 比較大，差不多達到了0.9，意味著大部分人都可以快速向出口位置移動。但隨著時間步的增加，平均速度快速減小，也就是擁堵在快速形成。當到200 步左右時，平均速度下降的速度很快就變慢了，同時幾乎達到了一個很低的穩定值，預示著出口位置拱形的擁堵已經形成。一直到3000 時間步前，平均速度基本上變化不大，這段時間也是疏散中最擁堵的時間段。緊急情況下，一旦拱形擁堵人群內部在此時間段有人不小心摔倒，附近人員由于后面人員的影響很難控制自己的行動，極易發生踩踏事故，造成疏散人員的傷亡。從3000 時間步以后，平均速度快速上升，拱形擁堵得到緩解，剩下的大部分人員可以快速疏散出去。

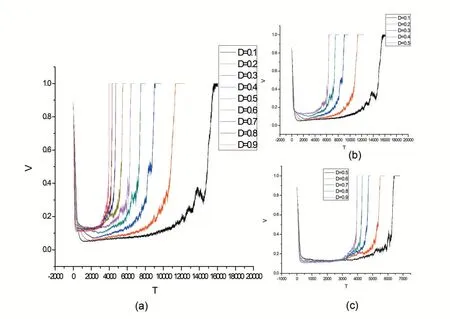
圖4 不同漂移系數D 下疏散平均速度與時間步的關系

我們知道模型中漂移系數D是一個重要參數，取值可以介于0 和1 之間的任何數值。當D=0，則是一個無后退的隨機行走；當D=1，就是行人在不被堵的前提下積極向前走。所以D值的不同反映了疏散人員心里緊急程度，D值越大越急于疏散出去，而D值越小則越不急。

圖4 是不同漂移系數D下疏散平均速度與時間步的關系圖。從圖中可看出D=0.5 是一個分界點。當D<0.5 時，D值越小平均速度達到的最小值越小，擁堵的程度越嚴重，同時D值越小擁堵的時間越長。D<0.5 時，這幾條關系曲線在T=50 左右有一個交點，如圖4 中（b）圖所示，也就是說當D<0.5 時系統演化超過50 個時間步時拱形擁堵基本上就形成了；當D>0.5時，D值越大平均速度達到的最小值越小，擁堵的程度越嚴重，但它們之間的差距很小，沒有D<0.5 時的差距明顯。同時當D>0.5 時，如圖4 中（c）圖所示，不同的關系曲線也有一個交點，這個交點在T=3000 左右，也就是說當D>0.5 時系統演化超過3000 時間步，擁堵基本上已經得到緩解，平均速度開始快速上升。結果顯示D值越大疏散時間越短，如圖5 所示，兩者呈現非線性關系。D值較小時，疏散時間隨著D值的增大減小的很快；當D值較大時，疏散時間隨著D值的增大減少的不很明顯。計算結果表明在人員疏散時，如果人員非常清楚出口位置，目標明確，可以較快疏散出去。

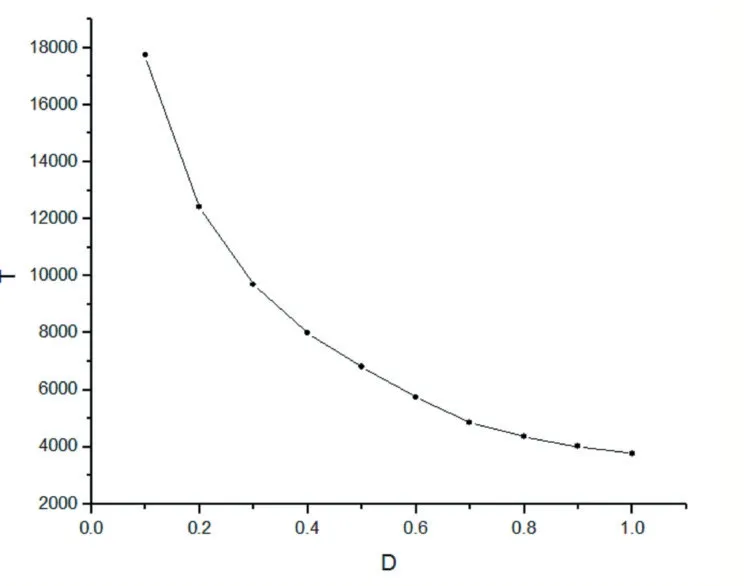
圖5 漂移系數D 與疏散時間關系

圖6 出口寬度與逃生時間的關系

出口寬度對疏散的影響我們也進行了模擬計算，結果如圖6 所示，可以看到疏散時間T隨著出口寬度W的增大非線性減小。疏散時間下降速率隨W增加由快變慢，其中W=7 是臨界值。當W<7 時，疏散時間隨著W的增大快速下降，所以W較小時，適當增加W值對疏散非常有益。當W>7 時，隨著W的增大，疏散時間減少得非常緩慢，W增加到一定數值后疏散時間幾乎沒什么變化。計算結果說明在實際應用中，出口寬度不應過小，這樣會造成疏散時間大大增加，一旦有火災等突發事件很不安全。而過大的出口寬度對人員疏散時間的減少意義不大。所以應當根據室內布局結構等實際因素確定其最佳出口寬度，并要確保出口寬度至少要大于上述臨界值。

3 結語

采用修改后的無后退隨機行走模型對單出口室內人員疏散問題進行了研究。模擬結果不但出現典型拱形擁堵，而且發現了拱形擁堵的不對稱消堵現象，即“快者越快”現象。平均速度與疏散時間關系中出現了長長的穩定擁堵階段，而此階段一旦出現偶然不利因素很容易造成大面積人員傷亡的慘劇。漂移系數對疏散有比較明顯影響，不同漂移系數下平均速度與時間步關系呈現出差異性，并且發現兩個臨界點，T=50 和T=3000，T=50 是擁堵形成的臨界點，而T=3000 是拱形擁堵開始消失的臨界點。同時漂移系數與疏散時間也呈現出非線性關系。通過出口寬度對疏散時間的影響研究，發現它們也呈現非線性關系，通過對關系曲線分析我們找到了一個最佳出口寬度推薦值，這對實際應用有一定價值。緊急情況下人員疏散有很多突發因素，例如疏散人員意外摔倒等都會對疏散造成影響，而人員心理和建筑物結構等或多或少也會影響疏散，所以人員疏散是一個很復雜也是有很大的實際應用的問題，需要我們進一步研究。