河流-承壓含水層系統壓力傳導系數的譜分析
呂國棟 楊啟紅 王俊智

摘 要:含水層對河水的響應程度與含水層的壓力傳導系數密切相關。借鑒多孔介質熱運移的相關研究成果,推導得到了河流-承壓含水層系統壓力傳導系數的功率譜解析表達式,進而提出了一種聯合使用河水位和地下水位觀測數據估算承壓含水層壓力傳導系數的新方法。采用該方法,應用螺山水文站水位數據和洪湖地區承壓地下水位數據,估算了長江洪湖地區承壓含水層的壓力傳導系數,結果表明:該方法估算得到的壓力傳導系數為1.6×104~8.7×105 m2/d,平均值為1.8×105 m2/d,與非穩定抽水試驗和數值模型反演得到的結果2.5×104~3.8×105 m2/d具有較好的一致性,功率譜分析是估算承壓含水層壓力傳導系數的有效方法。
關鍵詞:譜分析;河流-承壓含水層系統;壓力傳導系數;地下水位;洪湖
中圖分類號:X522 ? 文獻標志碼:A
doi:10.3969/j.issn.1000-1379.2020.04.016
Abstract: The response of aquifer to river is closely related to the aquifer diffusivity. By referring to studies of heat transport in porous media, this paper presented a power spectral method to estimate the confined aquifer diffusivity. This method was applied to the Honghu Lake area of the Yangtze River. Fluctuations of the Yangtze River in the Luoshan Hydrological Station and of the confined groundwater in the Honghu Lake area were used to estimate the aquifer diffusivity by using the power spectral method. The estimated aquifer diffusivity ranges from 1.6×104 to 8.7×105 m2/d with an average value of 1.8×105 m2/d, which is consistent with the results of 2.5×104-3.8×105 m2/d obtained from the transient pumping test and the inverse of a numerical model. Hence, the power spectral analysis is effective in the estimation of the aquifer diffusivity of confined aquifers.
Key words: spectral analysis; river-aquifer system; aquifer diffusivity; groundwater level; Honghu Lake area
河流和含水層之間的相互作用研究對于水文循環及河流附近生態環境建設具有重要意義。含水層對河水的響應程度與含水層的壓力傳導系數密切相關。壓力傳導系數理論上等于導水系數與貯水系數之比,是表征彈性動態條件下承壓含水層中水頭傳遞速度的參數[1-2]。壓力傳導系數是進行各種水文地質計算的基本物理參數,對于水資源的評價與合理開發利用、水污染的防治與預警、濕地生態環境保護等研究具有重要的理論和實踐意義。
水文地質試驗(如抽水試驗、微水試驗等)、數值模型反演是獲取壓力傳導系數的常規方法[1-4]。通過觀測地下水位,基于非穩定流地下水運動方程,水文地質試驗依據特定的解析公式可以計算出含水層的滲透系數(導水系數)和貯水率(貯水系數),進而計算出壓力傳導系數。基于有限差分、有限元原理,建立地下水數值模型,以地下水位觀測值與模擬值的差值平方和為目標函數,通過率定水文地質參數使目標函數達到最優,從而實現壓力傳導系數的反演。地下水位對河水位的響應程度與含水層的壓力傳導系數密切相關,因此理論上講,根據地下水位對河水位的響應情況可以估算出含水層的壓力傳導系數。Hall等給出了河水位突變或連續變化情況下地下水位響應的解析解[5-7],這些解析解可以實現含水層壓力傳導系數的估算,并已廣泛應用于各種生產實踐活動[8-11]。
近年來,國外學者提出了一種功率譜分析方法[12],通過長期觀測河水和河床不同埋深處的溫度并計算其功率譜,成功估算了河床沉積物的有效熱傳導系數。由于熱運移方程與承壓地下水運動方程形式上較為相似[13],因此采用功率譜方法有可能實現承壓含水層壓力傳導系數的估算。筆者首先給出承壓含水層壓力傳導系數的功率譜解析公式,然后以長江流域洪湖地區為例開展實例計算,并與非穩定流抽水試驗和數值模型反演確定的壓力傳導系數進行了對比,以期為洪湖地區生態環境保護提供技術支持。
2 實例研究
2.1 研究區概況
洪湖地區位于湖北省東南部長江中游北岸三峽水庫下游,是我國重要濕地之一。該地區屬于典型的亞熱帶濕潤季風氣候區,雨季旱季分明,降水多集中于春夏兩季,年平均降水量為1 000~1 300 mm,年平均蒸發量為1 300~1 400 mm[14-15]。
該地區水文地質條件相對簡單,地下水主要以賦存于全新統沖、湖積多孔介質中的潛水和承壓水的形式存在[14-15],其中潛水主要賦存于淺部亞黏土、黏土、淤泥類土等細粒沉積物中,承壓水主要賦存于深部較粗的粉細砂和砂礫層中。潛水含水層的含水性和透水性相對較弱且不均一,厚度為6~14 m;承壓含水層分布較為廣泛,厚度普遍大于20 m,頂板多被長江切穿,且與之有直接水力聯系,是本次研究的對象。鑒于洪湖地區長江岸線相對平直,承壓含水層厚度變化相對不大,可以近似使用圖1所示的概念模型進行概化。
在石碼頭—小港布置了4眼承壓含水層地下水動態長期觀測孔[14-15]。這4眼地下水動態長期觀測孔井深約35 m,揭露承壓含水層頂板。石碼頭—小港剖面上游約25 km處的螺山水文站長期觀測長江水位。地下水長期觀測孔所記錄的承壓地下水位數據和螺山水文站所記錄的長江水位數據是使用功率譜分析法估算承壓含水層壓力傳導系數的重要資料。
2.2 數據及處理
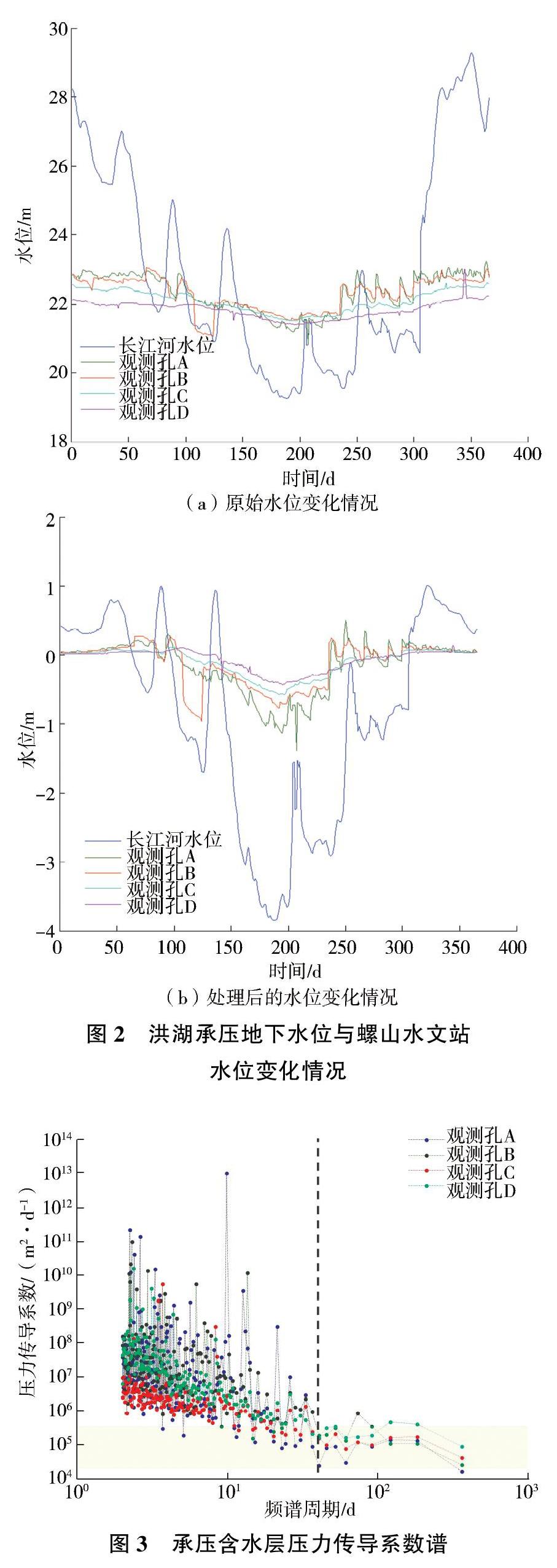
研究所采用的洪湖承壓地下水位動態數據和螺山水文站長江水位數據以“d”為分辨率,時間域為一完整水文年,即從2011年7月1日到2012年6月30日,共計366 d,見圖2(a)。洪湖承壓地下水位與長江水位波動步調基本一致,顯示出良好的相關性,表明兩者存在較為緊密的水力聯系。原始觀測數據顯示出較為顯著的規律性和隨機性波動。為消除規律性和隨機性波動對功率譜分析方法計算結果的干擾,需對原始數據進行“去趨勢化”和“漢寧窗”預處理。“去趨勢化”是用來去除原始觀測數據時間序列中的線性變化趨勢,“漢寧窗”可以減少傅里葉變換過程中的頻譜泄露,處理后的水位數據見圖2(b)。
2.3 結果及分析
基于傅里葉變換,將經“去趨勢化”和“漢寧窗”處理后的長江螺山水文站長江水位數據和4眼洪湖承壓地下水位數據代入式(3),計算得到其對應的功率譜。將計算得到的功率譜及觀測孔距離長江岸的垂向距離代入式(10),可繪制4眼地下水觀測孔的壓力傳導系數譜,見圖3。理論上講,概念模型將含水層概化為均質各向同性體,壓力傳導系數為一常數,對應的功率譜曲線為一水平直線。實際上,由于實測地下水位受氣象、地形、含水層非均質性等因素影響,因此功率譜曲線會發生系統或隨機偏移。對于洪湖地區,4眼地下水長期觀測孔的壓力傳導系數譜表現出較為一致的變化規律;在周期小于40 d時,壓力傳導系數波動強烈、不確定性大,主要受氣象、上游三峽水庫調蓄等因素引起的短期水位波動影響;在周期大于40 d時壓力傳導系數在105 m2/d附近,趨于穩定,綜合反映了地下水位的長期波動。因此,使用功率譜方法估算得到洪湖承壓含水層壓力傳導系數為1.6×104~8.7×105 m2/d,平均為1.8×105 m2/d。
圖3中灰色陰影為前人使用非穩定流抽水試驗或數值模型反演估算得到的壓力傳導系數的取值范圍。對于洪湖石碼頭—小港地區,胡望斌等[14]使用解析解方法建立了反映長江水位變化與承壓水動態的數學模型,模型中壓力傳導系數的取值為3.8×105 m2/d,是根據非穩定流抽水試驗得出的。此外,徐亮等[15]使用Modflow建立了石碼頭—小港地下水數值模型,并使用實測水位數據進行了參數反演,結果表明洪湖承壓含水層的滲透系數為20 m/d,彈性釋水系數為0.000 13~0.000 80/m,換算得到的壓力傳導系數為2.5×104~1.5×105 m2/d。對比發現,前人使用不同方法估算得到的壓力傳導系數的取值范圍與使用功率譜分析方法估算得到的結果有較好一致性,表明功率譜分析是估算承壓含水層壓力傳導系數的有效方法。與非穩定流抽水試驗和數值模型反演法相比,功率譜分析方法僅需借助前期觀測得到的河水位和地下水位數據,便可估算得到河岸帶尺度的含水層壓力傳導系數,具有良好的經濟效益和應用價值,可為洪湖地區生態環境保護提供技術支持。
3 結 論
借鑒多孔介質熱運移的相關研究成果,給出了承壓含水層壓力傳導系數的功率譜解析公式,可以實現河流-含水層系統承壓含水層壓力傳導系數的估算。洪湖地區承壓地下水位與長江螺山水文站水位具有良好相關性,使用功率譜方法估算了承壓含水層的壓力傳導系數,其與前人使用非穩定抽水試驗和數值模型反演法得到的結果具有較好一致性。功率譜方法可以有效估算承壓含水層的壓力傳導系數,可為洪湖地區生態環境保護提供技術支持。
參考文獻:
[1] 陳崇希,林敏.地下水動力學[M].武漢:中國地質大學出版社,1999:1-30.
[2] 薛禹群,朱學愚,吳吉春.地下水動力學[M].北京:地質出版社,1997:5-26.
[3] 陳崇希.地下水流數值模擬理論方法及模型設計[M].北京:地質出版社,2014:8-55.
[4] 薛禹群,謝春紅.地下水數值模擬[M].北京:科學出版社,2007:20-65.
[5] HALL F R, MOENCH A F. Application of the Convolution Equation to Stream-Aquifer Relationships[J]. Water Resources Research, 1972, 8(2): 487-493.
[6] SINGH S K. Aquifer Response to Sinusoidal or Arbitrary Stage of Semi Pervious Stream[J]. Journal of Hydraulic Engineering, 2004, 130(11): 1108-1118.
[7] 張蔚榛. 地下水非穩定流計算和地下水資源評價[M].北京:科學出版社,1983:214-292.
[8] HA K, KOH D C, YUM B W, et al. Estimation of Layered Aquifer Diffusivity and River Resistance Using Flood Wave Response Model[J]. Journal of Hydrology, 2007, 337(3): 284-293.
[9] OH Y Y, HAMM S Y, HA K, et al. Characterizing the Impact of River Barrage Construction on Stream-Aquifer Interactions[J]. Water, 2016, 8(4): 137.
[10] GIANNI G, RICHON J, PERROCHET P, et al. Rapid Identification of Transience in Streambed Conductance by Inversion of Floodwave Responses[J]. Water Resources Research, 2016, 52(4): 2647-2658.
[11] 尹立河,張俊,王曉勇,等.基于地下水對洪水響應的含水層水力參數反演[J].人民黃河,2014,36(10):58-60.
[12] WRMAN A, RIML J, SCHMADEL N, et al. Spectral Scaling of Heat Fluxes in Streambed Sediments[J]. Geophysical Research Letters, 2012, 39(23): 234.
[13] CARSLAW H S, JAEGER J C. Conduction of Heat in Solids[M]. Oxford: Clarendon Press, 1959: 18-78.
[14] 胡望斌,王學雷,陳世儉.洪湖地區淺層承壓水動態模擬研究[J].華中師范大學學報(自然科學版),2003,37(1):119-122.
[15] 徐亮,陳世儉,向先富,等.基于Visual Modflow的洪湖石碼頭—小港剖面地下水數值模擬[J].華中師范大學學報(自然科學版),2008,42(2):299-303.
【責任編輯 呂艷梅】

