雷達地物回波建模方法與應用

謝永亮 胡 輝 劉尚富

(海軍士官學校 安徽蚌埠 233032)

0 引言

實際雷達對地物的顯示是一個自然而然的事情，設計人員從來不需要關心地物應該怎樣分布、應該怎樣顯示，一旦雷達設計完成，雷達終端上就會呈現地物回波，這些地物回波可能是孤立的建筑物，也可能是連綿的山脈、廣闊的平原，甚至可以是城市、農田等等。可見，地物的顯示是一個非常復雜的課題，要模擬出逼真的地物回波，就必須研究地物顯示的建模問題，解決好這個問題，是提供逼真的地物回波的必要條件。

當前對地物回波的模擬通常根據雷達的作用距離、分辨力、波瓣和工作頻率等參數，結合雷達RCS，對雷達地雜波信號進行數學模型的建立與研究。當前使用的雜波模型主要有三種，第一是雜波幅度和功率譜統計模型；第二是雜波散射單元的機理模型；第三是由試驗數據擬合的與頻率、仰角、環境參數等參量之間相互作用的關系模型[1]。但這些方法對于將地物轉化為雷達顯示器上的回波涉及并不多，且研究也未進入深度發展，本文將從入射余角、RCS以及回波的統計特性對地物回波的建模與仿真應用進行研究論證。

1 入射余角對地物回波的影響

地面物體在雷達顯示器呈現的回波對雷達操作員來說是干擾雜波，稱為地雜波，又可作區域雜波。區域雜波是影響雷達探測的重要因素，尤其是入射余角較低時，這類影響更為明顯。其中入射余角、雷達波長、表面粗糙度及其散射特性對雷達雜波散射系數構成的影響最大。從雷達波長來說，雷達波長越長，雜波散射系數σ0越小[2]。入射余角ψg，是波束中心與地平面之間的夾角，如圖1所示。

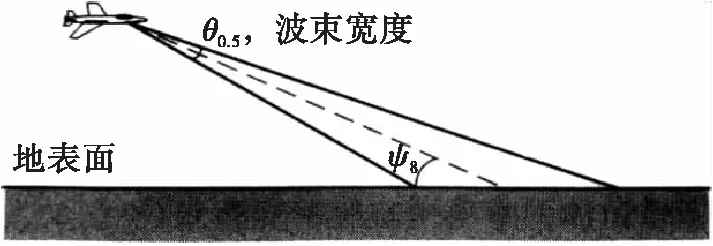
圖1 入射余角

σ0與入射余角的關系，一般可劃分為：高入射余角區、平坦區和低入射余角區。高入射余角區以相干的鏡像反射為主，散射系數隨入射余角增大而迅速增大。在平坦區以非相干散射為主，變化趨于緩慢。低入射余角區通常其散射系數隨入射余角的增長而飛速增長，又稱干涉區[3]。

低入射余角一般指的是從0到臨界角附近，比臨界角小的表面可看做是光滑的表面；大于臨界角的表面可看做粗糙表面[4]。按照瑞利準則，當表面高度起伏的均方根值為hrms，如果滿足式(1)時即可將表面認定為平坦表面，即

(1)

如圖2所示，當入射波照射到粗糙表面時，由于表面較為粗糙，起伏較大，比起光滑表面的路徑而言要長2hrmssinψg，這種路程差可以轉換為相位差Δφ，即

(2)

其第一個零點Δφ=π，臨界角ψgc可按公式(3)(4)來算出

(3)

或可表示為

(4)

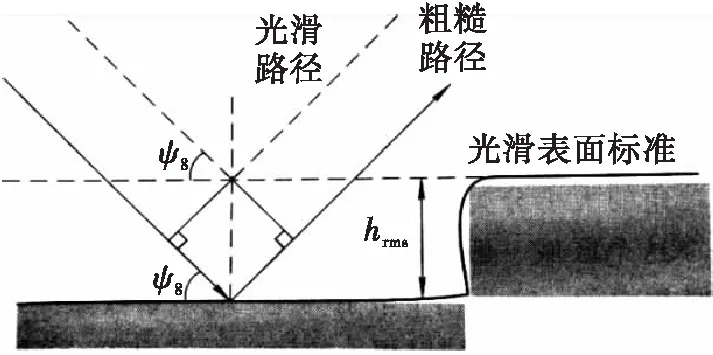
圖2 粗糙表面

2 地物回波RCS的計算

地物回波包括從雷達主瓣進入的地雜波以及從雷達副瓣進入的地雜波，所以其雷達反射截面積RCS可表示為σc[5]

σc=σMBc+σSLc

(5)

其中σSLc是旁瓣雜波RCS，σMBc是主瓣雜波RCS，如圖3所示。

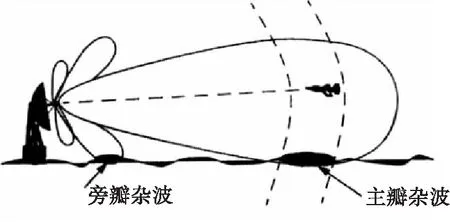
圖3 地物雜波幾何示意圖

為算出地雜波的RCS，必須先算出主瓣和副瓣對應的RCS。如圖4所示，假設目標高度為hr，雷達高度為hr，目標斜距是R，斜距在地平面上的投影由Rg表示，角度θA和θE分別表示方位和垂直維度的3 dB波束寬度，雷達距離分辨率為ΔR，主瓣雜波區的面積由AMBc表示，旁瓣雜波區的面積由ASLc表示。

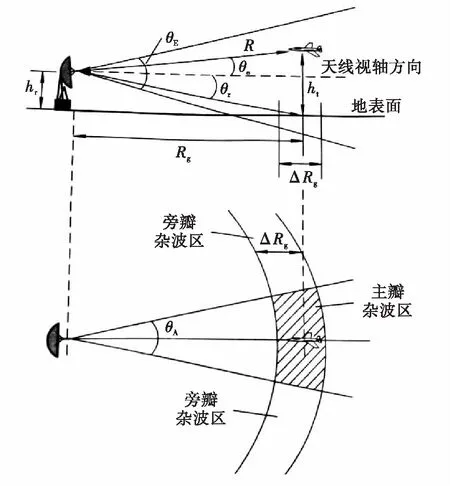
圖4 雷達雜波幾何圖(側視圖和下視圖)

由圖4可推導出

(6)

(7)

ΔRg=ΔRcosθr

(8)

Rg=Rcosθe

(9)

那么主瓣和旁瓣在雜波區的面積可表示為

AMBc=ΔRgRgθA

(10)

ASLc=ΔRgRgπ

(11)

如果雷達天線的方向圖函數為高斯型G(θ)

(12)

那么主瓣雜波和旁瓣雜波的RCS可表示為

σMBc=σ0AMBcG2(θe+θr)

=σ0ΔRgRgθaG2(θe+θr)

(13)

(14)

式(14)中SLrms表示雷達旁瓣電平的均方根值，σ0為地面雜波后向散射系數。

考慮到地球的曲率、傳播衰減和大氣折射的影響，地物回波的RCS可認為是隨距離R變化的函數[6]

(15)

3 地物回波RCS的統計特性

由于地物回波是由數量巨大的隨機分布的散射體組成，其相位和幅度均存在隨機性，通常用概率密度函數(pdf)來描述此類信號的特性。下面就雷達重點關心的地雜波的統計特性進行研究[7]。

地雜波與天線的照射角密切相關，實際上后向散射系數越大或照射的區域越大，地雜波強度越強。由于地面分布的物體、植被、質地、密度等不一樣，會引起地雜波的幅度變化，而這類隨機起伏特性在數學上通常采用概率密度函數和功率譜表示[8]。由于地雜波可以看作是數量眾多的散射體反射合成的總體效果，因此其統計規律可近似認為是高斯分布[9]

(16)

其幅度模型可用瑞利分布擬合

(17)

(18)

(19)

式中E[·]表示統計平均。

如果在雷達作用范圍內，不僅僅存在數量巨大的小散射單元，還有類似角反射器、雷康等強目標時，其統計規律不再符合高斯分布，用萊斯(Rice)分布更能表征其特性

(20)

其中，μ為均值，σ2為方差，I0(·)為第一類零階貝塞爾函數。

圖5就高斯分布、瑞利分布、萊斯分布分別畫出了其概率密度函數圖。

除此之外地雜波還可以認為是一種隨機過程，根據維納理論，還需要引入其相關特性，通常用功率譜來描述地雜波的相關特性[10]。

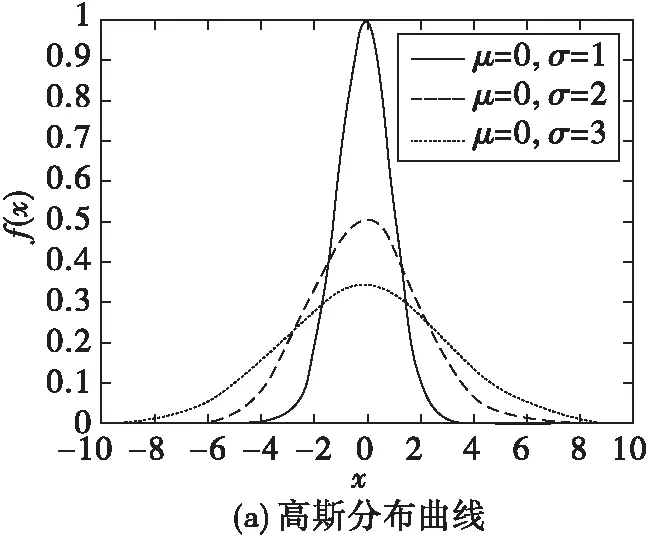
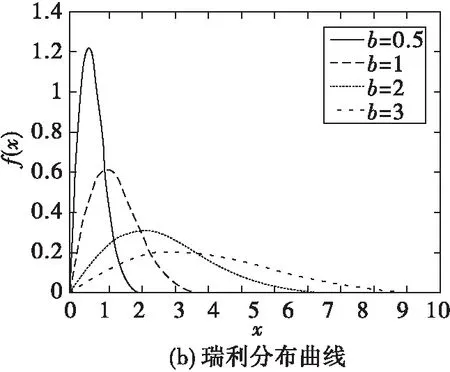
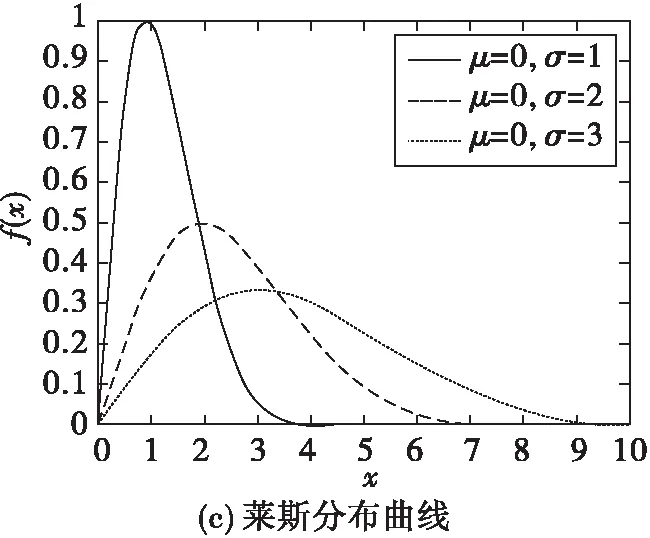
圖5 高斯、瑞利和萊斯分布的概率密度函數

一般地，地雜波可以采用高斯譜為

(21)

其中，S0為雜波平均功率，fd為地雜波的中心多普勒頻率，σf為地雜波功率譜的標準偏差(譜寬)。

(22)

其中，σν為雜波速度的標準偏差，與地雜波區植被類型和風速有關。

當地雜波中的高頻分量比較強時，需要更能擬合高頻分量的功率譜函數來表示。通常采用的有全極譜或指數譜。全極譜表達為

(23)

其中，fc稱為歸一化特征頻率，fd為地雜波多普勒頻率中心，當n取2是即為柯西譜，當n取3是即為立方譜。

指數譜可表示為

(24)

其中，fd為地雜波的多普勒頻率中心，fc稱為歸一化特征頻率。圖6分別畫出了其對應的功率譜。

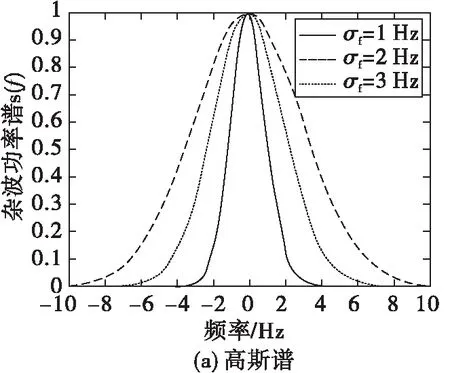
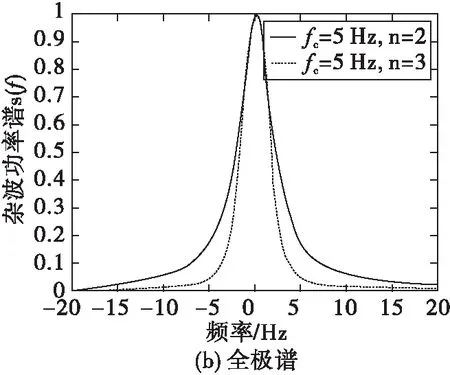
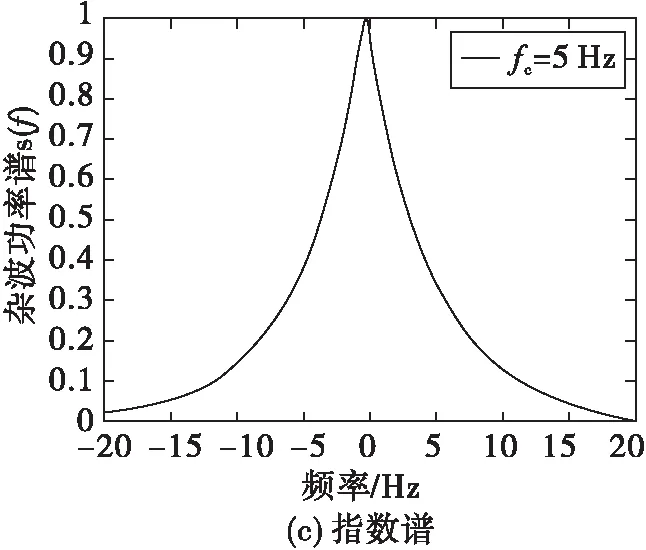
圖6 高斯型、全極型和指數型功率譜

4 地物回波模型的仿真應用

模擬地物回波，首先要計算地物的RCS。由式(15)可知，先應計算σc，可采用公式(25)計算[11]

(25)

其中：

σ0—地面雜波后向散射系數；

c—光速；

τ—脈寬(脈壓后的寬度)；

R—目標斜距；

θ—波瓣寬度，以弧度計算；

φ—入射余角。

假設某雷達τ為2 μs，波瓣寬度θ為2°，設定的地雜波類型為山脈，根據前面的不同入射余角對回波的影響，不同入射余角其對應的后向散射系數σ0見圖7所示。

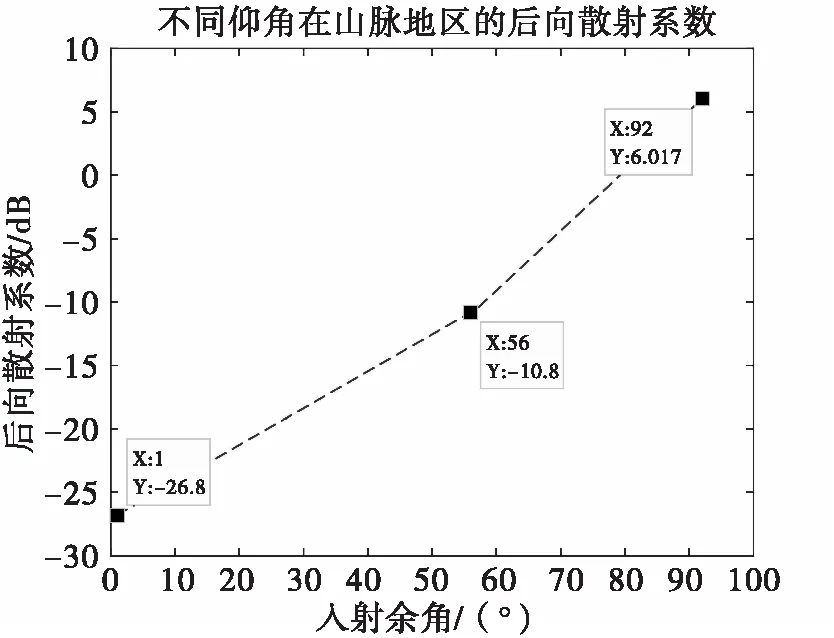
圖7 山脈地區不同仰角對應的后向散射系數

入射余角的計算與具體地形相關，對于非山區(城市)，地面可以視為平坦地面，地物傾角可以視為0；對于山區，則需要考慮地物的傾角[6]。考慮傾角的情況見圖8所示。

圖中α為山體傾角，h為山體高度，β為雷達仰角。計算入射余角φ的公式為

(26)

設h為400 m，L為5000 m，則φ是R的變量，其對應關系如圖9所示。

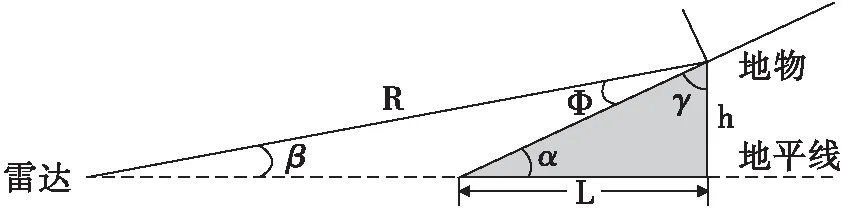
圖8 地物反射幾何模型

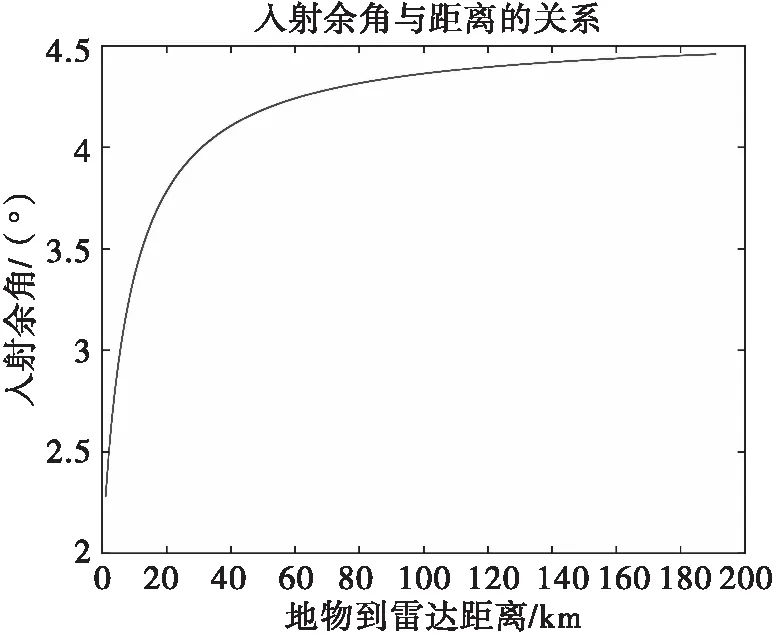
圖9 入射余角與距離的對應關系

根據以上計算結果，可以由式(15)計算出各雜波位置的等效雷達反射截面積。

計算出地物雜波的等效雷達反射截面積后，就可以開始對地物雜波進行仿真了。首先在地圖數據讀取地物高程數據，在后臺繪制地雜波，通過翻轉將繪制的地物雜波圖像呈至前臺。地雜波的繪制流程如圖10所示。

根據掃描線驅動逐個方向進行雜波的計算和繪制，繪制效果如圖11所示。從雷達模擬的仿真效果來看，較為逼真地模擬了實際地物的回波，既滿足了操作員對雷達環境的直觀感受，又滿足了雜波中的目標檢測操作。

圖10 地雜波繪制流程

圖11 地物回波在模擬器中的顯示效果

5 結束語

在仿真訓練與模擬器中，地物回波的模擬是一個重要的環節。本文首先分析了雷達入射余角對地物回波的影響，在此基礎上對地物回波建立了相應的數學模型，考慮到地物的起伏性和相關性，加入了地雜波的統計特性，并通過實例仿真模擬了較為逼真的地物回波畫面，驗證了建模方法的合理性和可操作性。在建模過程中，尚未充分考慮多徑效應、天線方向圖、脈沖壓縮等對地物回波模型的影響，加入這些要素對回波的調制后，模擬效果將與實際回波趨近，這是下一步重點研究的方向。