“數學分析”中各類積分對稱性定理的統一性解釋
艾正海,孫 峰
(樂山師范學院 數理學院,四川 樂山 614000)
0 引言
數學專業的“數學分析”[1-3]里涉及的各種積分的對稱性是一個重要知識點,這類知識點是各類考試的考點和熱點,合理利用對稱性解題不僅會起到事半功倍的作用,而且也很有趣。同時,這些常見的積分類也是近現代數學的基礎之一[4],雖然目前關于探討各種積分的對稱性文獻[5-10]層出不窮,但這類文獻往往僅介紹某一類積分的對稱性,或者雖然介紹了各類積分的對稱性,卻開篇列出各種對稱性定理,然后談及應用。這類文獻適合基礎扎實的讀者,但對于絕大多數讀者而言,由于這些對稱性定理眾多又相似,使得讀者難以記住和區分,特別地,第一類曲線(面)積分與第二類曲線(面)積分的奇偶性對稱性容易混淆,再加上各種對稱輪換性定理,就使得對稱性更加復雜。當學生都難以記憶這些對稱性定理的時候,應用也就更無從談起了。
由于近二十年來大學的擴招,使得高校教育轉變為大眾教育,而不是精英教育,學生學習上缺乏自主性和主動性[11],數學功底相比以前的學生也有了較大的距離[12],在這種情形下,教學改革變得緊迫和勢在必行[13]。另一方面,部分高校對“數學分析”的教學學時不得不進行壓縮,在課時較少時[13],如果我們單獨對各類積分對稱性進行詳細探討,學時也不允許。正如上文提及:這類知識點又是各類考試的考點和熱點,特別地,一些想繼續深造的同學經常問各種對稱性的問題,鑒于此,如何對這些積分對稱性進行精煉濃縮地講解,又能讓即使基礎薄弱的學生也能很容易區分和記住這些對稱性,是一個迫切要解決的問題。因此,本文對各種積分的對稱性進行統一性探討,以期有效地提高學生的學習能力。
1 定積分知識的簡單回顧
為了更好地理解后續內容,定積分知識的簡單回顧是必要的。
定理1 假設f(x)在[-a,a](a>0)為連續函數,則有

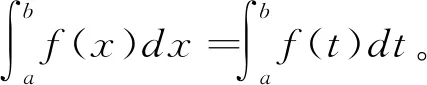
此定理說明定積分的值與積分變量無關。
2 重積分的對稱性及應用
傳統的對稱性定理從關于x、y、(x,y)等的奇偶函數去描述,較為繁雜。本節從對稱性和定義出發,給出這些二重積分對稱性定理的簡要解釋和快速記憶方法。當把二重積分對稱性搞清楚了,三重積分的對稱性直接類推,非常容易地寫出,因此本節不討論三重積分的對稱性。
定理3 設f(x,y)在有界閉區域D上連續,則有:
(a)設積分區域D關于y軸對稱,則
其中D1=D∩{x≥0};
(b)設積分區域D關于x軸對稱,則
其中D2=D∩{y≥0};
(c)設積分區域D關于原點對稱((x,y)∈D?(-x,-y)∈D),則
其中D3為D的右半平面或上半平面部分;
(d)設積分區域D關于直線y=x對稱,即((x,y)∈D?(y,x)∈D),則
?D4f(x,y)dσ=?D5f(x,y)dσ,

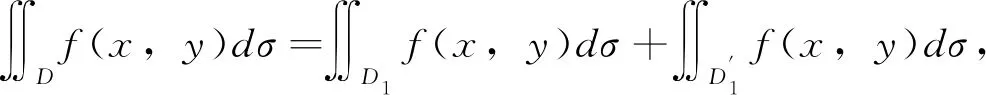
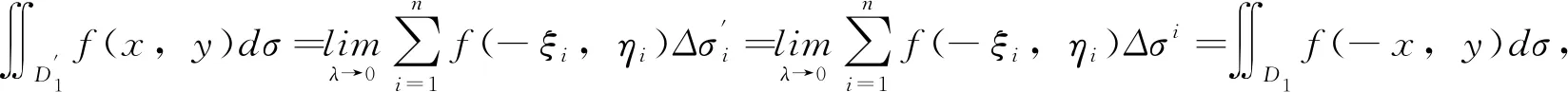
?Df(x,y)dσ=?D1f(x,y)dσ+?D1f(-x,y)dσ,從而(a)結論成立。
記憶方法:首先,確定點(x,y)關于y軸對稱的點明顯為(-x,y),再次,研究f(x,y)與f(-x,y)之間的關系:若f(x,y)=f(-x,y),即不變號;若f(x,y)=-f(-x,y),則變號。dσ為面積元,始終不變號。所以定理3可以記憶為:先找對稱點,再看對應的二個函數之間是否變號(由于dσ為面積元,始終不變號),變號為0,不變號為2倍。
以(c)為例:首先,(x,y)關于原點對稱的點明顯為(-x,-y);再次,研究f(x,y)與f(-x,-y)之間關系;最后,若變號(即f(x,y)=-f(-x,-y))則為0,不變號則為2倍。利用這個方法,我們很容易寫出積分區域D關于直線y=-x對稱時的情形,請讀者自行補充。
定理4 設f(x,y)在有界閉區域D上連續,若積分區域D關于x,y具有輪換對稱性,則
?Df(x,y)dσ=?Df(y,x)dσ
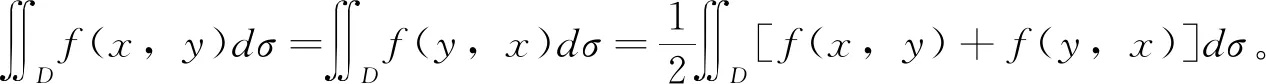
從上面的分析我們可以看出:對稱輪換性的本質為二重積分的值與積分變量如何選取是無關的,這與我們之前提出的定積分的性質是類似的。下面通過例1、例2來說明在計算二重積分值時,如何利用對稱性來有效地減少計算量。
例1 計算Ι=?D(3x+2y)2dσ,其中D:x2+y2≤1。
解Ι=?D(9x2+4y2+12xy)dσ,由于D關于x軸對稱,而f1(x,y)=12xy=-f1(x,-y),即變號了一次,故?D12xydσ=0。由于區域D明顯地關于x,y具有輪換對稱性,因此,?Dx2dσ=?Dy2dσ。
進一步可得:
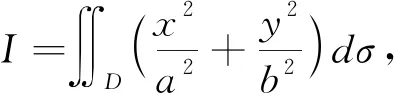
分析 因為D關于x,y具有輪換對稱性,故可以運用定理4。
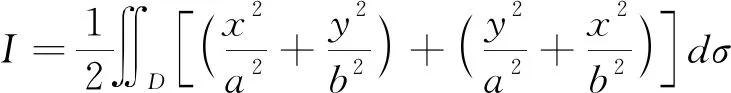
3 二類曲線積分的對稱性與應用
由第一類曲線積分與第一類曲面積分的定義可知,二者的對稱性是一致的;而第二類曲線積分與第二類曲面積分的定義仍然揭示了它們對稱性也是一致的。因此,在本節我們僅僅討論二類曲線積分的對稱性與應用,這足以說清對稱問題,對于曲面積分的對稱性,讀者可以直接類推得出。
首先,同上節一樣,列出二類曲線積分的最核心的對稱性定理。
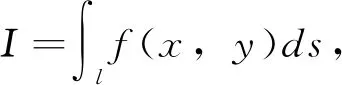
(a)若l是關于y軸對稱,則
其中l1={(x,y)|(x,y)∈l,x≥0};
(b)若l是關于x軸對稱,則
其中l2={(x,y)|(x,y)∈l,y≥0};
(c)若l是關于原點對稱,則
其中l3={(x,y)|(x,y)∈l,x≥0,y≥0};
(d)若l是關于y=x對稱,則
其中l4={(x,y)|(x,y)∈l,x≥y}。
定理6 設L為平面上分段光滑的定向曲線,其中P(x,y),Q(x,y)是連續的。則
(a)若曲線L是關于y軸對稱,則有
其中L1是L右半平面部分。
(b)若曲線L是關于x軸對稱,則有
其中L2是L位于x軸上方的部分。
對于第一類曲線積分的對稱性(定理5),仍然采取與二重積分對稱性相同的分析法和記憶法,也容易看出二者的對稱性結論類同,主要原因在于ds為長度的微元,仍然為正。對比定理5,定理6(第二類曲線積分的對稱性)明顯復雜于定理5(第一類曲線積分的對稱性)。如果要求學生強行記憶,勢必隨時間推移定理結論易混淆。對此,我們仍然按照之前第二節中的介紹方法來處理,以(a)為例:
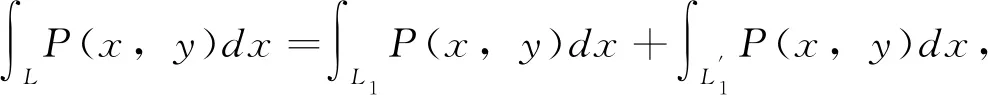
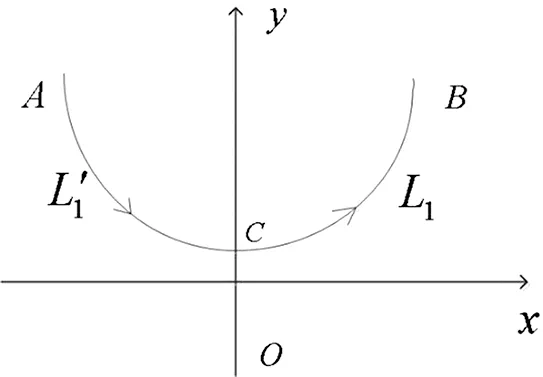
圖1 定理6(a)示意
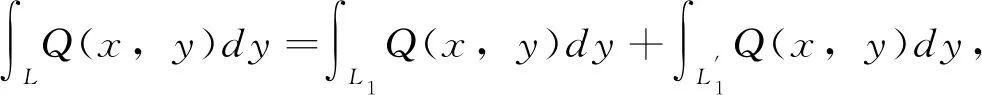
從上面的分析可以看出,對于第二類曲線積分,一方面考慮被積函數是否變號,另一方面考慮dx或dy是否變號,變了一次號為0,變了二次為2倍。關于原點對稱、關于y=x對稱,讀者可按上述方法很容易給出,故在此不再列出。
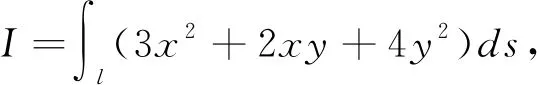
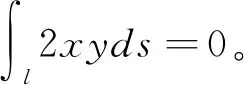
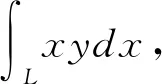
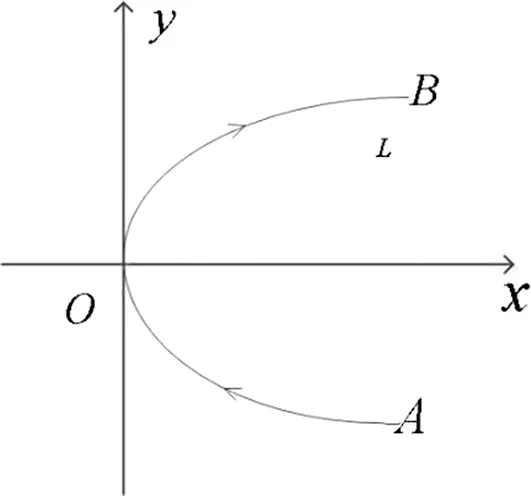
圖2 曲線L
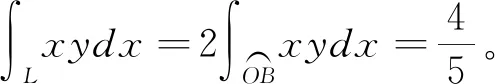
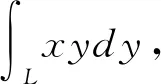
4 小結
本文討論了各種積分的對稱性,基本涵蓋了數學專業“數學分析”里的各種積分;突破傳統的各種積分對稱性分別闡述的模式,也不再考慮各種繁雜的奇偶性,找出了這些積分關于對稱性的共性,通過利用各種積分定義和類比定積分的手段,有效地解決了對各種積分對稱性記不住和容易記混淆的問題。總體來說,各種積分對稱性定理分四步走:一看積分區域(曲線、曲面)是否具有某種對稱性,此為前提;二寫對稱點,看被積函數在此種對稱性下是否發生了變號;三看微分在對稱區域上(區間、曲線、曲面等)是否發生了變號;最后看被積函數與微分總共變了幾次號,1次為0,2次為2倍。通過四步,無需再死記硬背各種積分的諸多對稱性定理。此外,輪換對稱性在多元積分里第一次出現,我們通過類比定積分,指出各種積分輪換對稱性的本質為積分值與用什么積分變量無關,使其容易被理解。按照本文提出的方法,讀者可以很輕松地寫出當積分區域(區間、曲線、曲面等)關于y=-x對稱和積分區域關于y=ax+b(a≠0)對稱的相應對稱性定理。總之,通過本文提出的四步走方法,各類積分的各類對稱性定理變得清晰易記。

