“同心鼓擊球”運動時力度與軌跡變化調整策略

崔冉冉 葛立蕓 姜 科

(1.青島理工大學管理工程學院，山東 青島 266520；2.青島理工大學信息與控制工程學院，山東 青島 266520)

1 問題分析及假設

首先，我們分析了理想狀態下球和鼓的運動，得到時間軌跡如圖1。

為了將球的跳動方向由傾斜狀態改為豎直狀態，需要調整鼓的傾斜角度，使得鼓的傾斜角度和球的跳動方向的傾斜角度相同，以此來抵消球的水平方向分速度。假設第i個隊員在ti時刻發力，隊員對發力時機的誤差為1s。Fi是沿繩方向的恒力。Fi可分解為水平方向和豎直方向2個方向上的分力。水平方向分量僅作用于空心鼓的水平移動，鼓面傾斜僅取決于豎直方向分量。在描述隊員的發力時機和力度與某一特定時刻的鼓面傾斜角度的關系時，可只考慮Fi的豎直分量。將鼓面傾斜看做剛體定軸轉動，該項目的道具是一面牛皮雙面鼓，可將鼓簡化成薄壁圓筒。

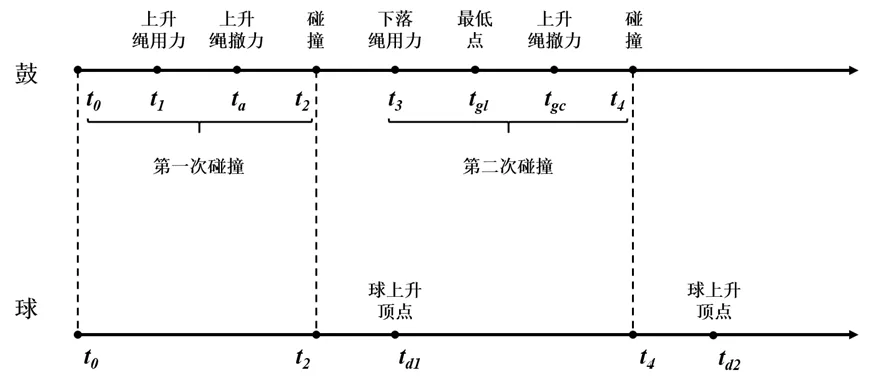
圖1

其中，λ為環密度。依據垂直軸定理

Jz=Jx+Jy

因為圓環任意兩個方向對稱，所以

Jx=JyJz=mR2(Jz為均勻圓環的轉動慣量)

而經分析可知，僅豎直分量對鼓的旋轉有影響，將所有豎直分量的力矩相加得到總力矩和：

對于此式，應在不同時間段分階段計算總力矩和，下面為力與時間的函數關系：

將鼓面傾斜視為剛體定軸轉動，由剛體定軸轉動定律可求得鼓轉動的角加速度：

Mz=Jcβ

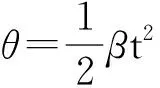
而調整鼓的傾斜角度可考慮以下方案：僅改變部分隊員的用力大小，所有隊員的發力時機相同；僅改變部分隊員的發力時機，所有隊員用力大小相同。由于球的傾斜角度介于2位隊員之間，因此僅需要調整球的傾斜角度兩側隊員的發力策略。

為了更好地解決問題，本文在此給出以下假設：

(1)假設忽略鼓和排球運動過程中的空氣阻力；

(2)假設忽略鼓和排球撞擊過程中的阻尼運動，不計能量損耗；

(3)假設隊員們無差別，即簡化為n個相同的隊員站成圓形，初始時刻每個隊員以相同姿勢手握繩子末端，能使得鼓面保持平行狀態；

(4)假設忽略雙面牛皮的重量，鼓可簡化成薄壁圓筒；

(5)由于鼓傾斜度角度較小，假設其對繩夾角大小和力矩的影響可以忽略；

(6)假設其它未考慮因素對所求結果影響不大。

2 模型的建立

第1步：隊員間距離應滿足大于0.6m的條件：

第2步：由幾何關系可知，鼓最后的傾斜角度與撞擊前瞬間排球速度與豎直方向夾角相等。由拋物線運動的性質：初速度與豎直方向的夾角和下落到相同高度時速度與豎直方向夾角相等，即：δ=φ

第3步：給定其余隊員的用力大小，將2位隊員的發力大小設為未知數，計算所有隊員對于鼓的轉動軸的力矩和所有隊員產生的總力矩：Mi=ri×Fi

第4步：所有隊員產生的總力矩應該與球的傾斜方向在水平面的投影垂直：Mz·rσ= 0

求得鼓的角加速度并求出合力矩：

Mz=Jcβ

利用以下公式將弧度轉化為角度：

由以上可求得這2位隊員的用力大小。

3 模型的求解

方便起見，假設0.11s時隊友施加力后，鼓的傾斜角度為預定值；隊員間距離等于0.6m。代入8位普通隊員的用力大小為80N，即：Fi=80N，i=3，4，…，10

得到2位隊友的用力大小分別為：F1=77.407879N；F2=78.674985N

即在發力時機相同的時候，隊員1用力77.407879N，隊員2用力78.674985N。

對于另一種情況：所有隊員大小相同，部分隊員發力大小不同，計算方式與此類似，不再贅述。

4 策略的現實意義

(1)實際情況下，所有隊員的發力情況不可能被精準控制，排球和鼓在空氣中運動會受到的空氣阻力，撞擊過程中還存在阻尼運動和能量損耗。故此，調整策略的實施效果有折扣，但對球方向的調整有積極作用。

(2)本文對于維持鼓面平行的模型可以推廣至工地塔吊高空運輸平衡器的研發，乒乓球、網球等拍擊球類運動中，調整球類運動軌跡的分析中。