基于NSGA-Ⅱ的發動機冷卻風扇葉片優化設計

孫新飛，尹明德，才旺

(南京航空航天大學 機電學院,江蘇 南京 210016)

0 引言

隨著汽車設計的多樣化和功能的日益增多，汽車前艙零部件的布置也越來越緊湊和復雜，發動機熱負荷問題日益突出，這對冷卻系統設計提出了較高的要求。冷卻風扇是發動機冷卻系統中最主要的零件，對冷卻系統的散熱性能有直接的影響，其氣動性能的優化是一個值得研究的課題。隨著汽車零部件市場競爭的愈演愈烈，在優化產品開發流程中，運用先進開發技術提高產品性能成為了企業提升競爭力的有效方式。國內外對冷卻風扇的氣動性能優化問題已經進行了大量的探索，但相關研究較為單一，未能形成系統化流程。朱傳敏等[1]對某款汽車冷卻風扇進行CFD分析，探究了葉片傾角、輪轂比和轉速對風扇氣動性能的影響規律；HURAULT J[2]重點研究了風扇的彎掠技術對性能的影響；吉林大學的習羽[3]利用 Fluent 軟件對風扇進行建模仿真，重點研究導風罩、進氣端等輔助部件和結構參數對氣動性能的影響。

1 風扇參數化建模

本文基于UG二次開發平臺，通過參數化造型方法對原風扇模型進行參數化重構。固定部分控制參數，調整幾個重要參數即可方便、直觀地實現模型的更新。沿葉片徑

向選取10個截面，建立各截面二維翼型，按照安裝角、弦長和彎掠積疊線對二維翼型進行坐標變換，對得到的三維翼型進行蒙皮后即可得葉片曲面，然后陣列葉片，添加輪轂、外環等實體即可完成風扇建模。本文選取安裝角和周向彎曲積疊作為設計變量。各個截面的安裝角分別使用3次Biezer曲線擬合；周向彎曲即為二維翼型周向的位移，同樣使用3次Biezer曲線描述。

1.1 安裝角參數化描述

原模型沿著葉高方向的11個截面安裝角分別為-30°、-27.4°、-24.5°、-21.3°、-20.6°、-19.9°、-19.9°、-18.8°、-17.8°、-17.1°、-18°，定義初始安裝角為-30°，創建如圖1所示的由4個控制點構成的Biezer曲線作為分布規律的控制曲線，x軸表示徑向位置與葉高的比值，取值范圍為[0，1]，y軸表示各截面安裝角與初始值之比。默認起始點y坐標為1，將初始值和另外3個控制點的y坐標作為設計變量。

1.2 周向彎曲參數化描述

定義周向彎曲初始值為50mm，創建如圖2所示的由4個控制點構成的Biezer曲線作為控制曲線，x軸表示徑向位置與葉高的比值，取值范圍為[0，1]，y軸表示各截面周向位移與初始值的比值。默認起始點y坐標為0，利用另外3個控制點的y坐標作為設計變量。

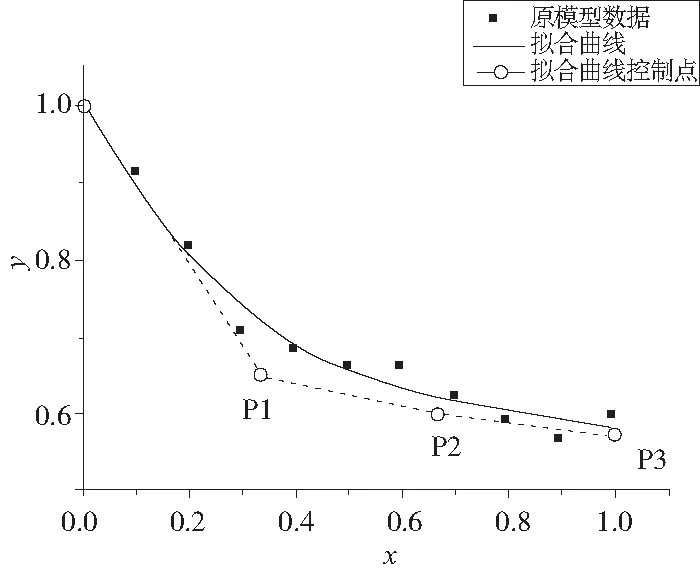
圖1 安裝角分布規律控制曲線

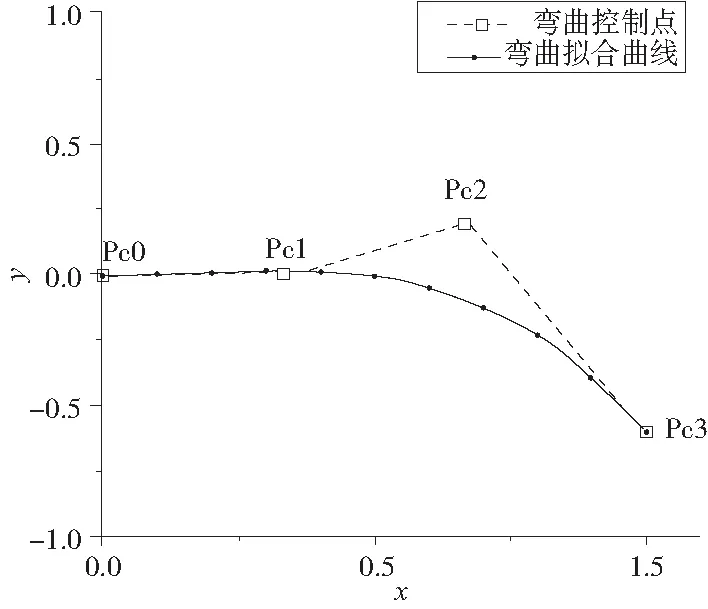
圖2 周向彎曲控制曲線

2 數值仿真模型與計算方法

2.1 流場數值模型建立

為盡量保證數值仿真的準確性，流場模型的建立需要綜合考慮試驗設備情況[4]和計算簡化要求，將流場模型分為進口區、出口區和旋轉流體區。出口區按照試驗設備尺寸設置為1 000mm×1 000mm×1 500mm的長方體，試驗設備的進口區為自由大氣。本文創建一個邊長1 000mm的正方體來模擬自由大氣進口。旋轉流體區是覆蓋整個風扇并摳除風扇實體的圓柱區域，是多重參考坐標系法(MRF)中定義轉速的一部分流場，是與風扇一起旋轉的區域，尺寸設置為直徑400mm，長度50mm。風扇流場數值模型如圖3所示。

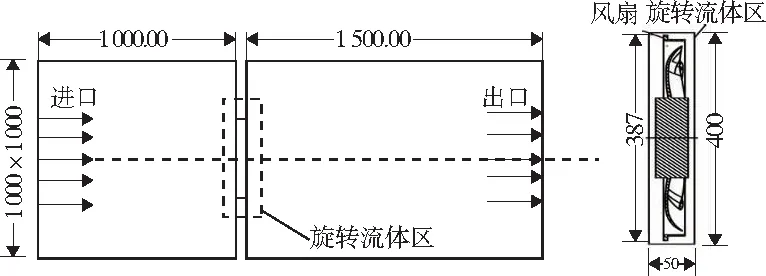
圖3 風扇流場模型簡圖

將創建的模型導入到ANSYS Meshing中進行網格劃分，針對不同區域制定不同的網格劃分策略。進、出口區形狀比較規則且實際流場平穩，選擇六面體結構網格；旋轉流體區曲面特征較多且流場梯度大，選用幾何適應性較好的四面體網格。網格劃分效果如圖4所示。

圖4 流場網格

2.2 邊界條件與計算方法

本文采用壓力進口和壓力出口邊界條件模擬試驗工況，設置進口相對壓力為0，出口靜壓為100 Pa；風扇表面設置為旋轉壁面，其他壁面設置為靜止壁面，旋轉流體區使用多重參考坐標系(MRF)方法，使旋轉流體區轉動起來，轉速設置為2 800 r/min；并設置旋轉流體區與進、出口之間的交界面(Interface)。使用定常計算得到出口流量和葉片轉矩的穩態結果；選擇RNGk-ε模型進行湍流模擬，使用SIMPLE算法進行求解，動量方程、湍流動能和湍流耗散項均采用二階迎風格式進行離散。設定殘差收斂條件為1×10-4，最大迭代次數為2 000。

3 基于CAESES的風扇參數化優化過程

風扇氣動性能優化的目的是尋求一定的參數組合，使得目標工況下流量盡可能大，消耗功率較小。本文結合近似模型和智能優化算法對風扇氣動性能進行多目標優化。首先確定設計變量及其取值范圍，通過試驗設計進行樣本采集，以數值模擬的結果建立目標函數與設計變量的近似數學模型，最后使用NSGA-Ⅱ多目標遺傳算法對近似模型進行尋優。整個過程基于CAESES多學科優化平臺使仿真優化過程完全自動化，其優化流程如圖5所示。

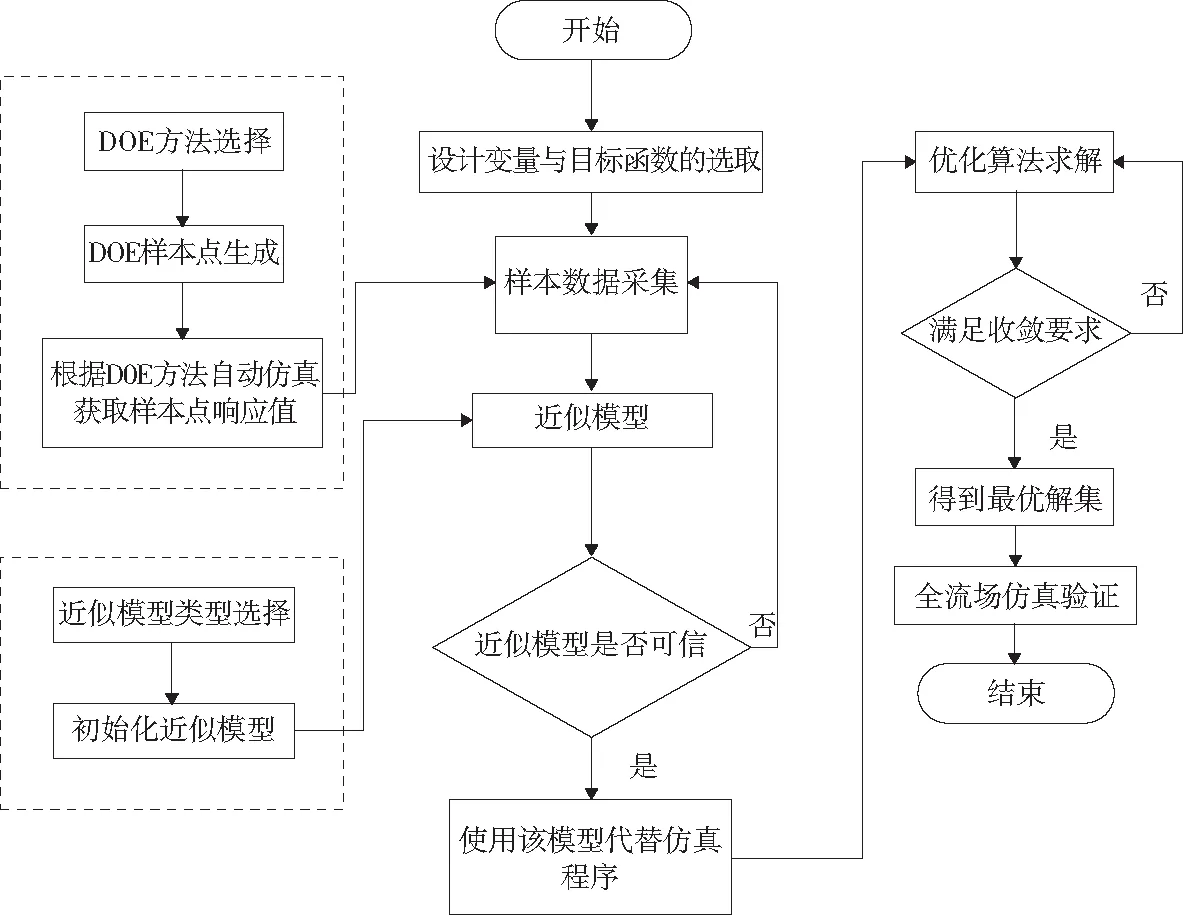
圖5 優化流程圖

3.1 平臺搭建

CAESES是一款多學科優化平臺，可以通過集成和驅動各類CAD/CAE軟件，快速建立和管理復雜的仿真過程。本文基于CAESES搭建發動機冷卻風扇自動仿真優化平臺，將風扇參數化設計模塊、網格劃分軟件和仿真計算軟件Fluent集成在一起，通過調用批處理命令啟動各個模塊，并讀取和修改相應的腳本程序，實現軟件間數據交換。再通過其內置DOE方法和優化算法進行優化設計，實現整個仿真優化流程，圖6為軟件集成框圖。

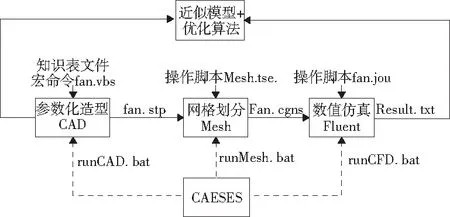
圖6 軟件集成框圖

3.2 試驗設計與近似模型

基于原始模型的初始值，參考相關文獻確定設計變量的取值范圍如表1所示。

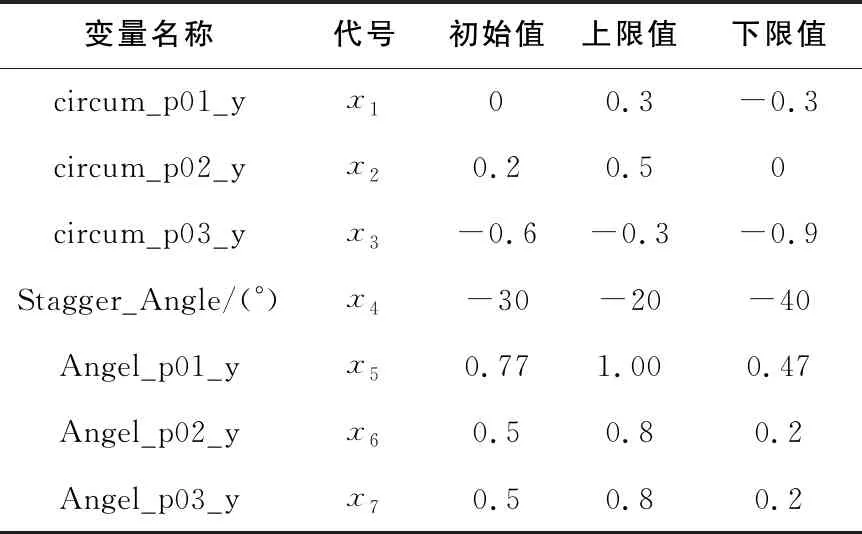
表1 設計變量及其取值范圍

試驗設計(DOE)方法是通過合理安排試驗，以較小的試驗規模獲得理想試驗結果的方法[5]，為構建近似模型提供樣本數據。本文選用最優拉丁超立方設計方法，該方法具有較好的空間填充性和均勻性。近似模型是利用已知樣本數據，通過擬合、插值等數學手段預測未知點響應的數學方法。常用的近似模型:響應面方法、徑向基神經網絡和Kriging模型等[6]。本文基于試驗設計得到的45組樣本數據，建立7個設計變量與2個響應的響應面模型。

3.3 優化算法

對于本文的多目標優化問題，實際工程優化應用最多且較為成熟的是第二代非支配排序遺傳算法(NSGA-Ⅱ)，它引進精英策略，保證某些優良的種群個體在進化過程中不會被丟棄，從而提高優化結果的精度。采用擁擠度和擁擠度比較算子，不但克服了NSGA中需要人為指定共享參數的缺陷，也保證了種群的多樣性和優化結果的均勻性[7]。本文的NSGA-Ⅱ算法參數設置為交叉概率Pc=0.9，變異概率Pm=0.1，種群大小為40，進化代數為100。

3.4 優化模型的建立

本文以風扇流量和功率為目標函數，優化目標是提高流量，降低功率。設計變量為表1所示7 個葉片結構參數；約束條件則需要根據企業給定的最低性能要求設置，即為在靜壓 100Pa 的工況下，流量≥ 0.6m3/s，同時功率≤200W。建立的優化模型如下：

MaxQv=f1(x)

MinPes=f2(x)

Subject toQv≥0.6m3/s，Pes≤200W

式中：Qv為體積流量；Pes為功率；x={x1,x2,…,x7}。

4 優化結果及分析

對于多目標優化問題，各個目標間一般是相互沖突的，優化解不可能是單一的解，遺傳算法尋優得到的是Pareto最優解集。圖 7所示為求解得到的Pareto前沿，紅色點集表示不滿足約束條件，黑色點集表示滿足約束條件，藍色點集即為Pareto最優解集(本刊黑白印刷，相關疑問咨詢作者)。在4 000個計算點中Pareto前沿共有346個點，一般需要根據實際需求對這些設計點在兩個優化目標間進行協調權衡。本文引入功效系數法并結合企業實際需求，選取第209個點為最優解，結果如表2所示。

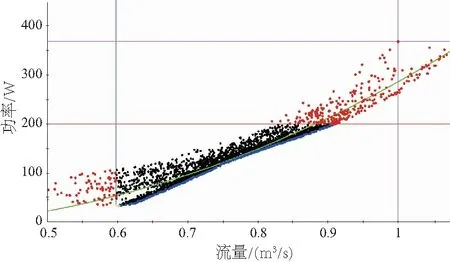
圖7 優化結果圖

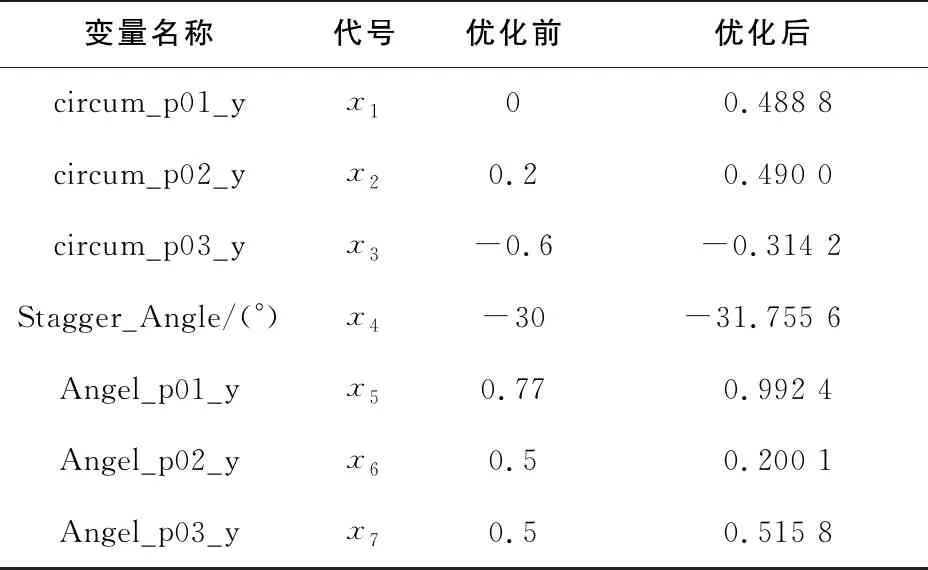
表2 優化前后設計變量對比

從優化后的變量數據可以看出，周向彎曲規律的3個控制點均有所增大，安裝角初始值有所增大且安裝角分布規律的第1、第3點增大，第2點減小。將優化結果反饋到參數化模型中去，得到優化的風扇模型如圖8所示，再對優化后的模型進行CFD仿真計算，與原模型的仿真值進行對比，達到了流量的提高和功率的降低，完成了優化任務。在目標工況點下，消耗功率由 170.32 W 降低到了 165.68 W，降低了2.72%。流量的提升則相對明顯，從0.762 8m3/s升高到0.837 6m3/s，有9.81%的提升(表3)。

從設計變量和目標響應的變化可以得出初步結論：安裝角增大可以增強葉片做功能力，增大流量，適度增強周向彎曲程度，可以使得流場跡線分布更加集中，抑制渦流的產生，從而增大流量減小功率。后續可進行更加深入的研究，探究各個變量對目標影響的作用機理。

圖8 優化前后模型對比圖

表3 優化前后性能對比

5 結語

針對汽車發動機冷卻風扇，本文使用參數化建模技術進行了模型重構。基于多學科優化平臺CAESES和流體仿真軟件Fluent，建立了集參數化建模、網格劃分、CFD分析和優化于一體的冷卻風扇智能優化平臺，選取周向彎曲

和安裝角分布規律的7個參數作為設計變量，目標工況點的流量和功率為優化目標，使用響應面近似模型結合NSGA-Ⅱ多目標遺傳算法對冷卻風扇進行了優化，優化后風扇流量提高了9.81%，功率降低了2.72%。研究表明本文采用的自動優化設計方法具有一定的工程應用價值。