超冷87Rb原子在二維光晶格中Mott絕緣態的實驗實現*

文凱王良偉周方陳良超王鵬軍孟增明? 張靖

1)(山西大學光電研究所,量子光學與光量子器件國家重點實驗室,太原030006)

2)(山西大學極端光學協同創新中心,太原030006)

(2020年4 月8日收到;2020年6月6日收到修改稿)

1 引 言

強關聯多體物理是研究諸多材料性質的關鍵內容,但是一直以來有兩個問題難以攻克,一個是計算難度隨系統的粒子數增多呈指數增長;另一個是非線性系統無法用微擾法處理[1].近年來,快速發展的光晶格因其具有完美的周期勢場和高度的可調控性,使得研究強關聯多體系統成為可能[2?8].2002年,德國Bloch小組首次在實驗上觀測到了玻色-愛因斯坦凝聚體(Bose-Einstein condensation,BEC)在光晶格中由超流(superfluid,SF)態相變到Mott絕緣(Mott insulator,MI)態,從此光晶格成為研究超冷原子強關聯多體系統中新奇量子態的重要手段[9].而對于自旋大于1/2的原子,光晶格又可以提供一個高度可控的大自旋量子關聯體系,在此基礎上,許多新材料模型和新奇量子現象被發現[10?16].利用單一激光光束折疊反射產生二維光晶格,這個方案已用于產生二維光晶格的雙阱陣列,實現分離和操控原子對陣列[17],并理論預測了該系統具有高軌道能帶的拓撲半金屬態[18].本文實驗觀測了87Rb超冷原子在兩種不同的二維光晶格中SF態和MI態之間的量子相變.二維光晶格是采用單束激光折疊反射產生,通過控制激光偏振產生兩種不同的二維光晶格結構, 一種是激光偏振方向平行于晶格光束所在平面, 另一種是激光偏振方向垂直于晶格光束所在平面. 該工作為今后開展光晶格中大自旋量子態和強關聯物理等研究奠定基礎.

2 理論模型

2.1 Bose-Hubbard模型建立

在1998年,Jaksch等[19]將Hubbard模型引入超冷原子領域,建立了Bose-Hubbard模型,提出了實現SF態到MI態轉變的條件.其模型包含三個關鍵參數:隧穿強度J,相互作用強度U和格點上的化學勢μi.二次量子化的多體哈密頓量在坐標表象下可寫成:

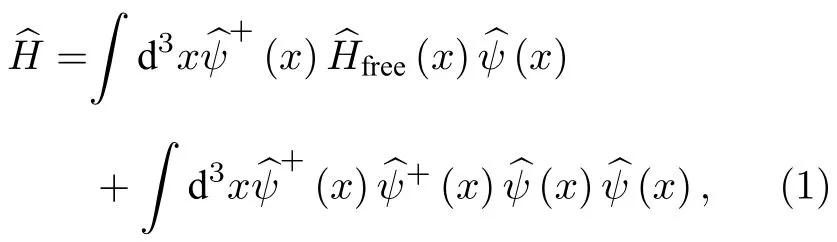
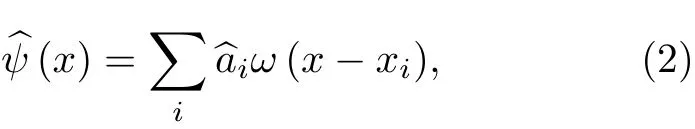
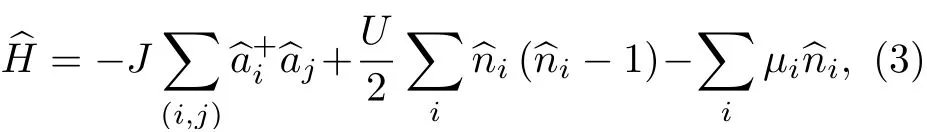
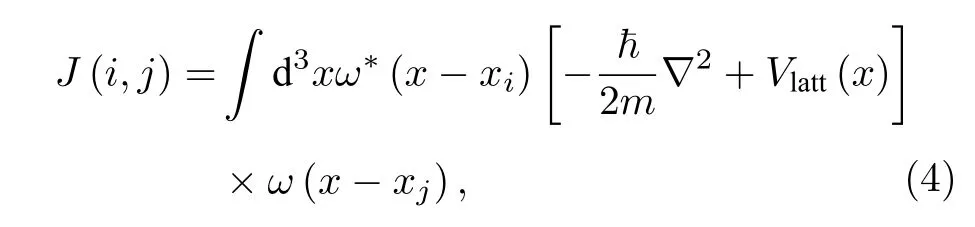
第二項表示單個格點上原子間的相互作用

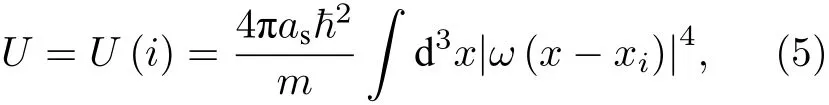
第三項為格點上的化學勢

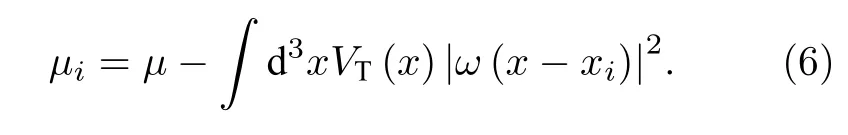
2.2 相變過程分析

Bose-Hubbard模型無法直接求解,所以考慮兩個極限情況[20].

當J/U→∞,即晶格間躍遷占主導,而相應的晶格勢趨近于零,即U→0,原子依然保持Thomas-Fermi分布,所有玻色原子在k=0的最低Bloch能帶,系統的波函數表現由單原子的波函數等相位疊加的形式,體系的基態波函數:

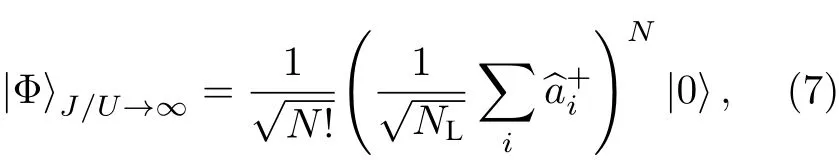
其中,N表示原子數,NL為晶格點,原子可以在格點間自由隧穿,單個格點上的原子滿足泊松分布,此時為超流態.當原子自由飛行時,由于相鄰格點原子之間具有相同的相位,所以在動量空間可以看到干涉產生離散的動量分量.如圖1所示處于超流態的原子在晶格中隧穿.

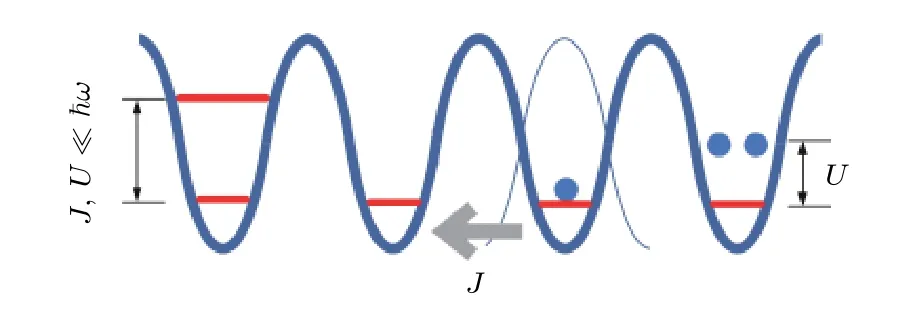
圖1超冷原子在光晶格中的隧穿Fig.1.The tunneling of ultracold atoms in optical lattice.

當J/U→0,晶格間相互作用占主導,即U→∞格點間原子隧穿很弱,晶格勢很強,系統的基態由局域化的原子波函數組成,則體系基態波函數為

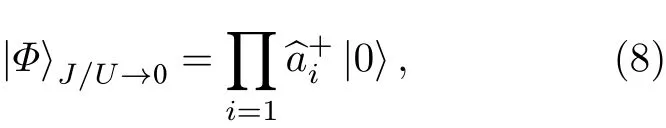
此時這一狀態為MI態,相鄰格點間沒有相干,所以在動量空間不會觀察到干涉產生的離散動量分量.

前面描述兩個極端情況下的Bose-Hubbard模型,考慮J/U從0 →∞ 即從SF態到MI態的相變過程,這主要由J/U和μi/U共同作用,如果MI態中單個格點中僅有一個原子,可以根據蒙特卡洛數值模擬出臨界點為(U/J)n=1=16.4[21].

3 實驗過程

圖2為產生二維光晶格的實驗光路圖.光晶格激光經過平面反射鏡M1、M2和平凹反射鏡M3的反射后,沿原光路返回,其中消色差透鏡F0、F1使激光會聚到原子的束腰直徑為200μm.

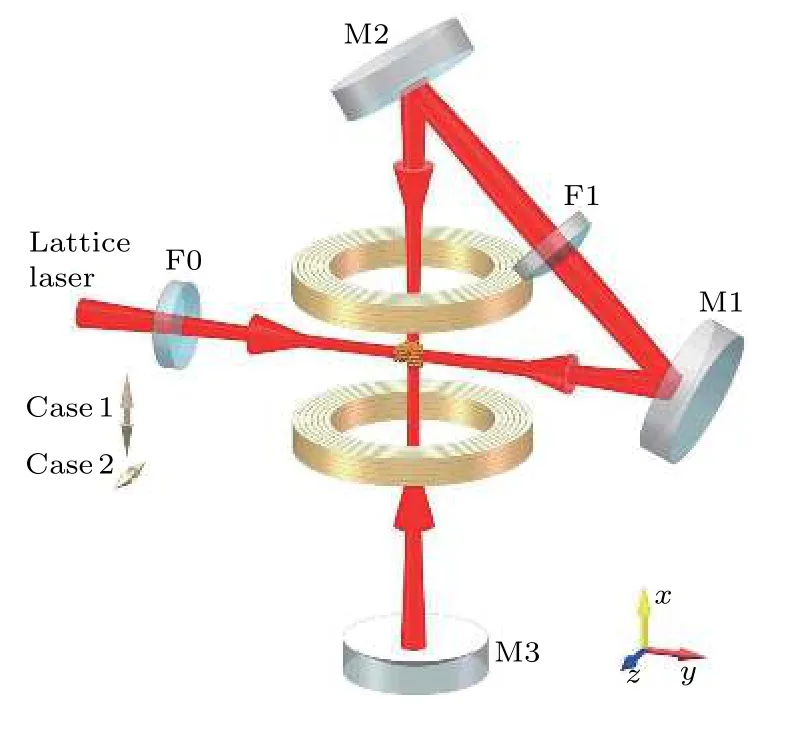
圖2實驗裝置二維光晶格由一束激光往返產生,其中方案1和方案2分別代表激光偏振平行和垂直于光束所在平面的兩種情況Fig.2.Schematic diagram of the experimental setup to realize the two-dimensional optical lattices.The two-dimensional optical lattices are made of a single fold retroreflected laser beam.The linearly polarization of the incident laser beam aligned parallel(case 1)or normal(case 2)to the drawing plane can generate two different cases of two-dimensional optical lattice potentials.

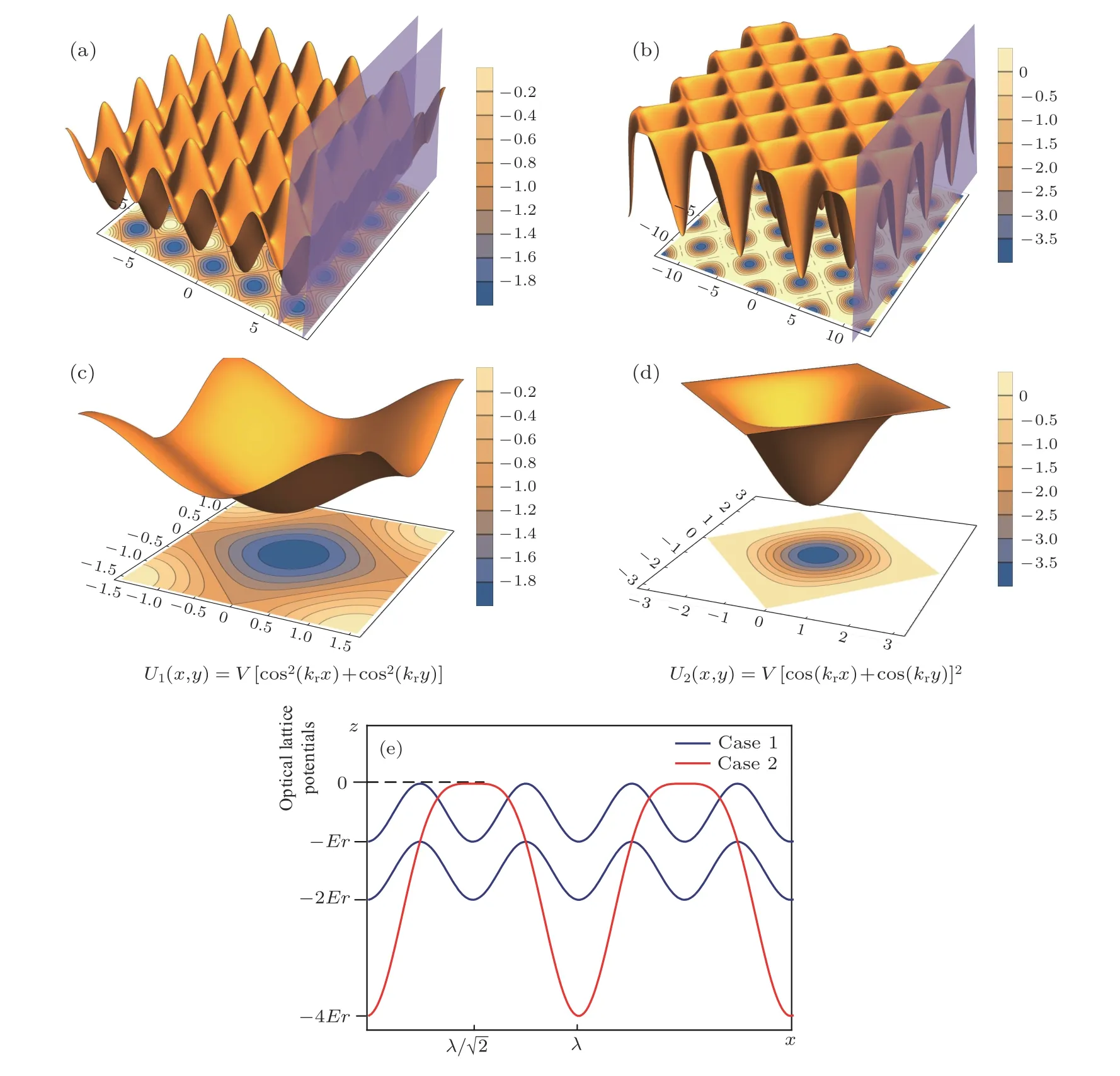
圖3兩種光晶格(a)方案1的面內光晶格空間分布;(b)方案2的面外光晶格空間分布;(c)方案1的晶胞;(d)方案2的晶胞;(e)兩種光晶格勢在xz平面上的分布Fig.3.Two types of optical lattices:(a)Spatial distribution pattern of in-plane optical lattice for case 1;(b)spatial distribution pattern of out-plane optical lattice for case 2;(c)unit cell for case 1;(d)unit cell for case 2;(e)the potentials of two types of optical lattices(V = –Er).

在本實驗中,通過改變激光偏振產生了兩種不同結構的二維光晶格.根據入射激光偏振的不同,具體分為兩種方案:方案1是激光的偏振平行于光束所在平面,由此產生的二維光晶格稱為面內晶格, 沿x軸和y軸是兩個獨立的一維光晶格, 所以勢阱為其中是光晶格激光的波長.面內二維光晶格勢阱的空間分布及在xz平面上的投影如圖3(a)所示,可以看到勢阱沿x、y軸獨立分布,空間周期為λ/2.方案2是入射激光偏振垂直于光束所在平面,產生的二維光晶格稱為面外晶格,因為沿x、y方向激光偏振互相平行, 所以兩個一維光晶格會產生干涉, 勢阱為其中2 cos(krx)cos(kry) 為干涉項,由圖3(b)可以看到勢阱沿x軸、y軸呈45°分布,周期為當波長為紅失諧時(V<0),光晶格產生的勢阱就像地平面上挖的一個個“洞”.近期本研究組將這兩種光晶格的相位信息寫到物質波上,產生了亞波長的相位結構[22].圖3(c)和3(d)分別表示的是面內晶格和面外晶格的一個晶胞.圖3(e)表示的是在相同光強和波長下,兩種光晶格勢在xz平面的分布,藍線代表方案1(兩條藍線對應圖3(a)中勢阱在xz面上最低和最高處的平面分布),紅線代表方案2,可以看到在相同情況下,面外光晶格勢阱更深,束縛原子的能力也越強,也更容易達到MI態.

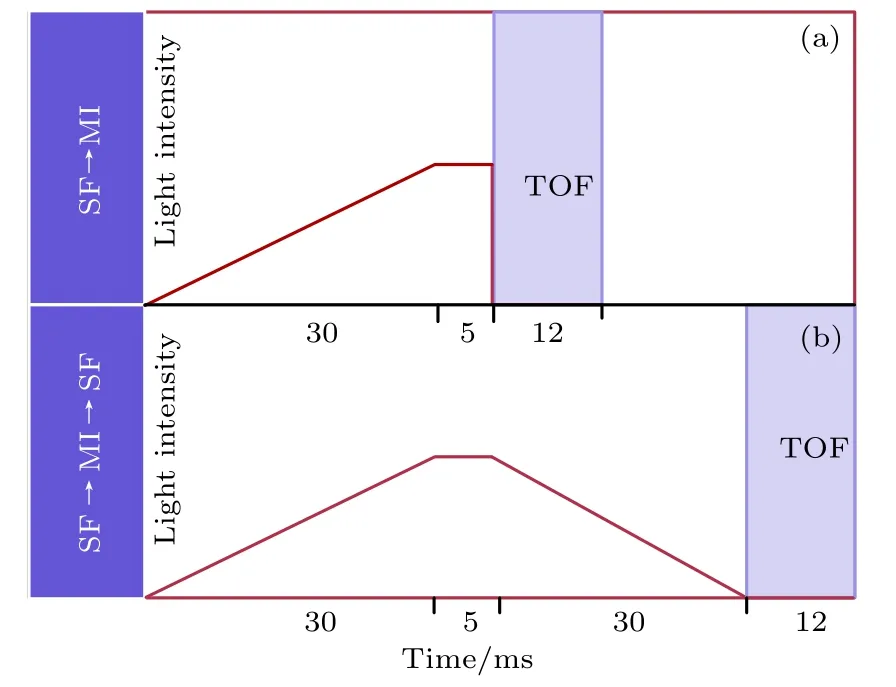
圖4實驗時序圖 紅色表示的光晶格光強的變化,最后自由飛行12 ms吸收成像,其中(a)表示SF到MI的時序,(b)表示BEC到MI再到BEC的時序Fig.4.Schematic diagram of the experimental sequence:The red lines show the light intensity of optical lattice,and finally have an imaging of TOF 12 ms.The drawing(a)shows the sequence of SF to MI,drawing(b)shows the sequence of BEC to MI,and back to BEC.

具體實驗過程如下:|F=2,mF=2?態的87Rb原子在四極磁阱和藍失諧光塞勢阱疊加形成的復合阱中進行射頻蒸發預冷卻[23?25],當原子溫度達到5μK左右時,將原子裝載到兩束激光交叉形成的偶極阱中(波長為1064 nm,頻率相差10 MHz,在原子云處的光斑直徑是200μm),通過進一步蒸發冷卻后,最終獲得2×105個87Rb原子的玻色愛因斯坦凝聚體[26,27].然后打開光晶格激光,將光強由零線性增大,用時30 ms,再等待5 ms,使原子在光晶格中穩定下來.時序如圖4(a)所示,紅線表示光晶格光強.在打開光晶格過程中光偶極阱功率保持不變,用于維持z方向的束縛,最后突然關閉偶極阱和光晶格勢阱,原子在自由空間中飛行12 ms后做吸收成像(time of flight,TOF),依據原子在動量空間中的分布,可以判定BEC是否相變到MI態;當獲得MI態后,降低光晶格光強到零,用時30 ms,最后同時關斷所有激光,自由飛行12 ms成像,即實現SF態到MI態再到BEC的量子相變,實驗時序如圖4(b)所示.

4 實驗結果和分析

實驗上首先研究了面內二維光晶格的量子相變過程.通過每次調節時序圖4(a)中的光強來觀察相變過程, 分別為0.92 mW(2.23Er)、3.7 mW(8.96Er)、10.67 mW(25.84Er)和13.26 mW(32.12Er),由此得到圖5中的(a1)、(a2)、(a3)、(a4),可以看到在弱光晶格下,在原子動量空間中心的上下左右四個正方向2kr處出現干涉的動量分量,表明原子處在超流態,隨著光強增大,格點間原子隧穿減弱,相互作用增強,格點間的干涉減弱,因此干涉的高動量分量對比度減弱.(a2)中在±45°方向上出現動量分量,這主要是由于偏振不純導致有少許面外光晶格的貢獻,實驗中用偏振分光棱鏡測得光束經過反射鏡M2時,消光比已經由1/1000變化到1.8/1000;其次是兩個方向上的光路無法保證完全垂直.當阱深加到32Er時,凝聚體徹底相變到MI態,此時每個格點內原子相互作用增強,由此導致格點間原子的相對相位隨機,因此干涉消失,此時原子彌散分布在連續動量空間里.Spielman等[28]采用單束激光產生二維光晶格,實驗觀測到87Rb原子在面內晶格中由SF態徹底相變到MI態的阱深接近31(2)Er,結論與本文實驗結果相一致.在圖5(a)的基礎上,分別將四次實驗的光晶格勢阱降到零,重新獲得BEC,分別對應(b1)、(b2)、(b3)、(b4),發現光晶格勢阱越深,返回得到的BEC中熱原子數也越多,原子溫度略有升高,主要是由光晶格抖動等不穩定性因素引起原子加熱.

之后實驗研究了87Rb原子在面外二維光晶格中的量子相變過程, 與方案1相同, 通過改變晶格光強來觀察相變過程,具體的光強參數為0.89 mW(2.15Er),2.3 mW(5.57Er)、4.2 mW(10.17Er)、5.1 mW(12.35Er),由此得到圖6中的(a1)、(a2)、(a3)、(a4),表示SF態相變到MI態的過程;隨后分別減小光強到零,得到各自對應的BEC,如圖6(b1)至圖6(b4).

在圖6(a)中,剛開始光強較弱的時候,格點間原子干涉占主導地位,首先在±45°方向上出現動量分量.逐漸增大光強,±45°方向上的動量分量也隨著增強,但對比度逐漸減弱.當光晶格強度達到10.17Er時,系統就發生量子相變,進入MI態.對比方案1和2可知,后者出現量子相變的晶格深度更低,這與之前的理論分析一致,因為面外晶格兩個方向的激光在原子處平行,由此產生干涉增強,而面內晶格的激光在原子處的偏振正交,因此是兩個獨立的一維光晶格構成的二維光晶格,勢阱深度的具體情況見圖3(e),面外光晶格的最低處能量是面內偏振光晶格最低處的兩倍,同時面外二維光晶格的勢壘高度是面內光晶格最低處勢壘的四倍,因此面外偏振相比面內偏振二維光晶格在較低光強下就可以產生MI量子相變.

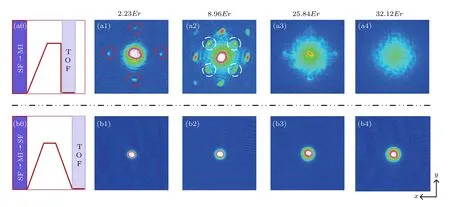
圖5方案1的量子相變(a0)表示獲得MI態的時序圖,(a1)到(a4)為SF態相變到MI態的過程,(a1)中紅色標注為光晶格格點,(a2)中白色標注的格點主要由于激光偏振不純、x軸和y軸方向上的光路不完全正交所導致的,當勢阱逐漸加深,隧穿開始加強,這些格點也越明顯;(b0)為BEC相變到MI態,再相變回BEC的時序圖,分別對應(b1)—(b4)Fig.5.Quantum phase transition for case 1:(a0)Reveals the sequence diagram of BEC to MI,from(a1)to(a4),show the imaging from SF to MI.In(a1),the red dashed circles show the lattice points,and in (a2),the white dashed circles show some incorrect lattice points,because the linearly polarization is impure and two beam paths along x axis and y axis are not totally orthogonal.Increasing potentials,these lattice points are more obvious;(b0)reveals the sequence diagram of MI to BEC,(b1)to(b4)show the imaging of MI to BEC after decreasing the potentials to zero.

5 結 論

本文采用單一激光光束的多次折疊反射方案實現了二維光晶格,進而通過控制面內和面外兩種偏振狀態產生了兩種不同結構的二維光晶格.將87Rb原子BEC裝載到兩種光晶格中觀察到從超流態和Mott絕緣態的量子相變,分析了兩種光晶格結構對量子相變的影響.下一步將從理論和實驗上精確定量分析兩種光晶格量子相變點的光強大小和相對比例,希望進一步研究與量子相變有關的許多有趣的多體物理現象.