鎂顆粒-空氣混合物一維非穩態爆震波特性數值模擬研究*

劉龍夏智勛? 黃利亞馬立坤陳斌斌

1)(國防科技大學空天科學學院高超聲速沖壓發動機技術重點實驗室,長沙410073)

2)(國防科技大學空天科學學院,長沙410073)

(2020年4 月14日收到;2020年5月9日收到修改稿)

1 引 言

固體粉末燃料(鎂、鋁和硼等)因能量高、易存儲、價格低廉,不僅在常規的固體推進劑領域得到廣泛應用,還可應用于爆震推進系統,如作為添加劑用于改善爆震波質量[1],提高脈沖爆震發動機性能[2],也作為連續旋轉爆震燃燒室主要燃料[3?7]等.鎂雖然能量密度低于鋁和硼,但鎂金屬較低的熔點和沸點使其點火特性和燃燒效率更優,其燃燒過程以液態顆粒蒸發后的氣相反應為主,反應速度比鋁和硼更快,因此應用于爆震領域更有前景.此外,工業生產中,鎂因反應活性比鋁和硼更高,發生爆炸事故的潛在風險更高,因此研究鎂的爆震燃燒過程對工業生產安全也具有重要意義.

在此前的研究中[8],已針對鎂顆粒-空氣混合物爆震,分析了來流速度、相變過程、顆粒初始濃度和顆粒初始粒徑等因素對爆震波穩態傳播特性的影響規律,但研究仍存在如下不足.

1)文中采用的鎂顆粒燃燒模型較為簡單,在鎂顆粒達到沸點前反應速率采用經驗公式[9,10],顆粒沸騰后汽化速率采用純液滴蒸發公式[10?12].而相關研究表明[13,14],鎂顆粒實際燃燒過程與純液滴燃燒存在不同,其燃燒產物氧化鎂中一部分會在顆粒表面凝結形成氧化帽.氧化鎂凝結時釋放熱量,使顆粒反應速率增大,同時生成的氧化帽則減小了顆粒表面的實際蒸發面積,使顆粒反應速率減小,因此有必要針對顆粒表面沉積對爆震波速度和結構的影響開展相關研究.文獻[8]中以鎂顆粒的汽化速率代替鎂顆粒汽化形成蒸氣而后與氧氣進行氣相反應的總速率,會導致貧氧工況下顆粒反應速率的計算值偏高.此外,文獻[8]假設鎂顆粒達到熔點后才開始反應,而相關研究表明,由于鎂的氧化層為非致密結構[15],在鎂顆粒達到熔點前,氧氣便可通過擴散穿過氧化層與鎂發生表面反應,只是熔化前鎂的表面反應速率明顯低于熔化后[16?19].

2)文中未考慮爆震波在管道內傳播時由壁面引起的損失.Zhang等[10]認為管壁摩擦及換熱損失會使前導激波后的氣相工質更快加速至聲速,進而對爆震波結構產生影響.洪滔等[20]認為,對于鋁顆粒-空氣混合物爆震,在考慮管壁摩擦及換熱損失的條件下,CJ面處有20%的鋁顆粒尚未反應,表明管壁造成的損失是影響爆震波傳播過程的重要因素之一.

3)文中未能體現爆震波傳播過程中的非穩態特性.穩態模型[8]的計算結果表明,在一個鎂顆粒初始濃度較低的小范圍內(0.146—0.168 kg/m3),受產物MgO的熔化過程的影響,對應的爆震波無法以一個穩定的速度傳播.此不穩定傳播過程的具體形式如何還需要通過非穩態模型開展進一步研究.此外,參照氣相爆震過程[21],因點火能量不同導致的DDT過程不同和因反應速率量級不同導致傳播過程中可能存在周期振蕩等問題,也需要開展相關研究.

鑒于現有研究存在的不足以及鎂顆粒燃料應用于爆震燃燒的優勢,本文通過建立鎂顆粒-空氣一維非穩態兩相爆震模型,分析研究燃燒產物MgO在顆粒表面的凝結、爆震管壁面熱損失、鎂顆粒初始粒徑、初始當量比等因素對爆震波傳播速度和結構的影響,以及初始點火能量、MgO熔化過程等因素對爆震波DDT過程、傳播過程穩定性等非穩態特性的影響,為鎂粉燃料應用于爆震推進動力系統奠定理論基礎.

2 數學物理模型

為便于計算,結合文獻[10]中建立的氣體顆粒兩相爆震模型,本文作出如下簡化假設:

1)顆粒均勻彌撒分布,作為連續介質處理,顆粒內溫度均勻分布,且初始粒徑相同.關于非統一初始粒徑的影響見本文3.4節;

2)在考慮表面沉積的條件下,鎂未完全蒸發前,顆粒相溫度不會超過鎂的沸點;

3)忽略顆粒間相互作用,忽略顆粒與壁面的作用,顆粒相壓強為0;

4)燃燒產物MgO算作氣相組分,氧化鎂的離解溫度當作沸點處理,物質沸點由Clausius-Clapeyron方程確定[22],氣相中僅氣態工質(氧氣、氮氣、鎂蒸氣和氣態氧化鎂)對氣相壓強有貢獻;

5)物質熔點為常數,相變潛熱包含在內能之中,在氧化鎂熔化、離解過程中,氣相溫度分別維持在氧化鎂熔點和離解溫度;

6)當顆粒粒徑減小至初始粒徑的十分之一時,顆粒質量僅為初始質量的千分之一,此時不再計算兩相間的相互作用[20].

2.1 流動控制方程組

流動控制方程組如下:

2.2 源項表達式

(1)質量源項

質量源項Sd分為異相反應Sd,het和蒸發Sd,eva兩部分,即Sd=Sd,het+Sd,eva.根據文獻[23]在顆粒 完全熔化之前表面發生緩慢的異相反應:

其中,R為通用氣體常數,YO2為氣相中氧氣質量分數,β表示根據鎂和氧氣反應的化學計量比得到的氧氣與鎂的質量比,r表示顆粒半徑.為簡化計算,在緩慢氧化階段(顆粒溫度在873—923 K),忽略顆粒表面生成的氧化鎂對顆粒粒徑的影響.顆粒完全熔化后,鎂顆粒燃燒過程與液滴蒸發燃燒類似,參照文獻[23,24]中處理方法,假設燃燒產物在顆粒表面沉積形成球冠狀氧化帽,此時顆粒表面蒸發速率為其中,Pr和Nu分別為Prandtl數和顆粒在強迫對流換熱條件下的Nusselt數,μg為氣相黏性系數,B為Spalding傳遞系數,其表達式為

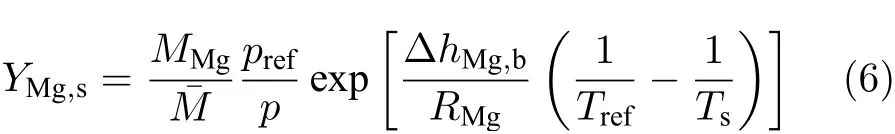
其中,Tref為鎂顆粒在參考壓力pref下的沸點,RMg為鎂蒸氣的氣體常數.MMg和分別為鎂蒸氣的摩爾質量以及氣相中氣態物質的平均摩爾質量.各組分反應源項表達式如下:

其中,qc,Mg表示鎂的單位質量熱值,Shom為單位體積內氣相中鎂蒸氣的消耗速率,根據文獻[23,25]有

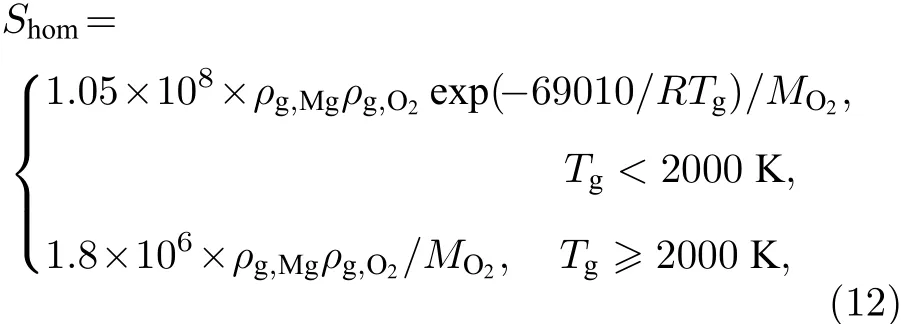
(2)兩相間作用力源項

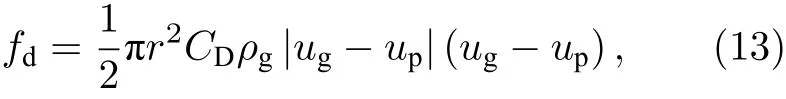
由于鎂顆粒燃燒過程類似液滴蒸發燃燒,顆粒與氣體之間存在質量交換,阻力系數CD表達式為

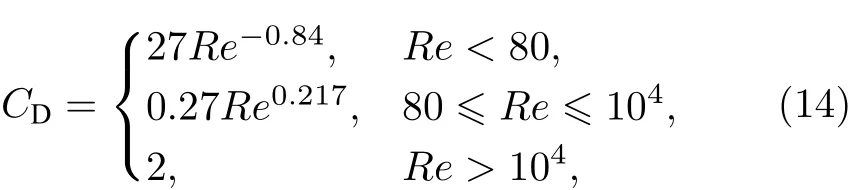
(3)兩相間換熱源項

兩相間對流熱傳導:

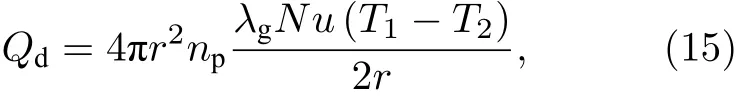
其中,λg為氣相導熱系數.對于可壓縮流動,強迫對流換熱條件下的Nusselt數,根據文獻[26]有:

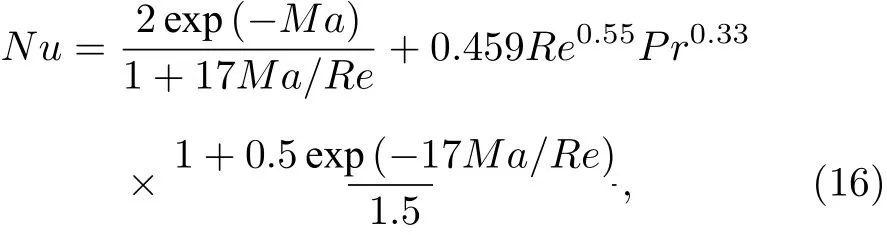
其中,Ma為氣固兩相速度差與當地氣相聲速的比值.

(4)兩相間換熱源項

壁面產生的黏性摩擦力為

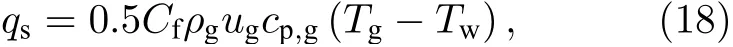
2.3 數值方法

本文數值計算方法采用CE/SE方法,它是一種格式簡單、精度高、捕獲爆震波等強間斷能力強的高精度計算格式,文獻[27,28]等將CE/SE方法應用于兩相混合物爆震研究,并驗證了其可行性.鑒于爆震問題中化學反應特征時間相對于對流特征時間要小得多,在數值求解過程中每個時間步的求解思路為:先不考慮方程組(1)中源項的影響,用CE/SE方法求解純流動方程組獲得流場參數,然后將作為初值,用4階Runge-Kutta法求解常微分方程組:

獲得下一時間步的流場參數.本文算例中Runge-Kutta法的時間步長為CE/SE法的1/10.

計算域左端為固體壁面,右端為出口,長度為40 m.計算域初始條件為ρg,0=1.29 kg/m3、ρp,0=0.445 kg/m3,ug,0=up,0=0 m/s,Tg,0=Tp,0= 300 K,r0= 2.5μm. 點火區位于固壁端, 其初始條件為ρg,0=3 kg/m3,ug,0=2000 m/s,Tg,0=3000 K,點火區長度Lign=0.288 m .圖1為t=2.5 ms時刻,網格大小分別為1 mm、0.5 mm、0.25 mm時所對應的流場中壓力的分布.算例中未考慮壁面摩擦、換熱損失以及顆粒表面沉積.由圖可知,1 mm網格計算結果與另外兩組有明顯差別,0.5 mm和0.25 mm的壓力分布幾乎相同,隨著尺度減小,激波間斷面所在位置有向下游移動的趨勢,且壓力峰值略有增加,但總體差別不大.為兼顧計算效率,本文采用0.5 mm的網格尺度進行計算.

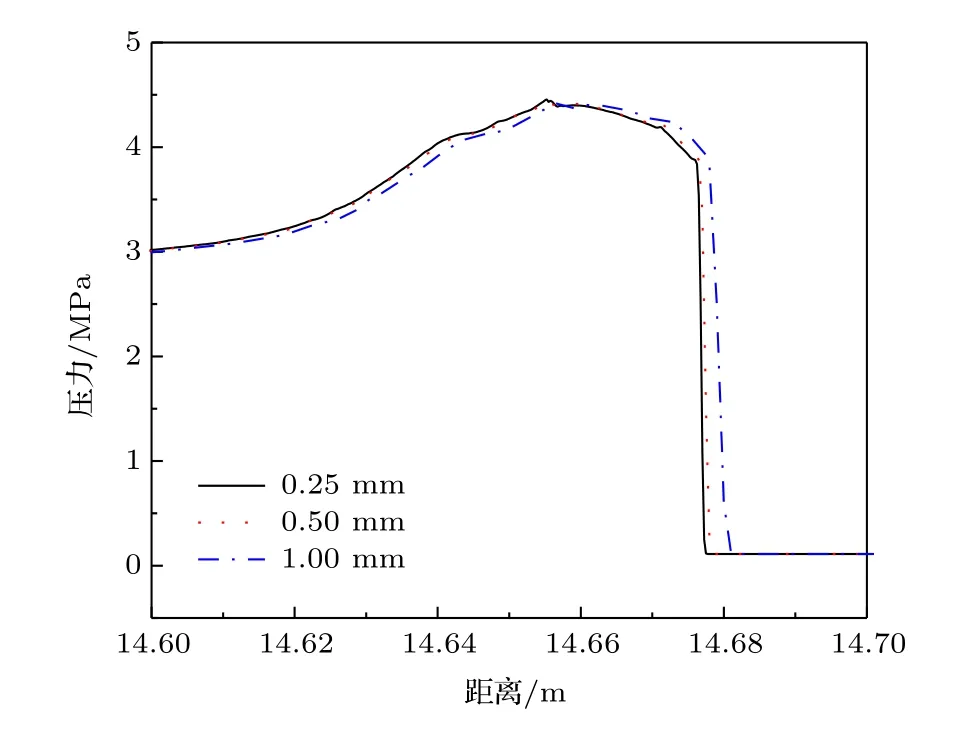
圖1不同網格尺度對應的壓力分布Fig.1.Spatial distribution of the gas-phase pressure with different grid sizes.

3 結果與討論

3.1 不同顆粒燃燒模型對比

ρg,0=1.29 kg/m3ρp,0=ug,0=up,0=Tg,0=Tp,0=r0=5將計算域初始條件,0.445 kg/m3,0 m/s,300 K,μm定義為標準參考條件,下文算例如無特別說明,則計算域初始條件以上述條件處理.

圖2為爆震波充分發展后趨于穩定傳播的狀態下,不同時刻爆震波壓力峰附近的壓力分布情況,時間間隔為0.05 ms.由圖可知,在爆震波趨于穩定傳播的狀態下,壓力峰值和壓力波形在傳播過程中仍存在小幅振蕩.根據文獻[21],對于采用單步反應模型的一維氣相爆震而言,爆震波傳播過程中出現周期性震蕩主要與反應活化能和反應放熱量有關.活化能較大時對應的反應高溫敏感性較高,較小的溫度擾動就會導致反應速率的大幅波動,而對于較高的反應放熱量,擾動的物理效應也會增強.對于鎂顆粒-空氣混合物爆震,其反應活性低于常規氣體燃料-空氣混合物,反應活化能較高,且鎂的理論當量空燃比較低,在相同空氣質量且當量比為1的條件下,鎂燃燒的反應放熱量高于常規氣體燃料.以上原因導致在傳播過程中燃燒區內鎂顆粒反應速率存在波動,因此鎂顆粒-空氣混合物一維非穩態爆震波傳播過程中存在振蕩現象.上述狀態下,爆震波傳播速度的振幅較小,在±1 m/s范圍內,可將振蕩平均值作為爆震波穩定傳播速度.后文如無特別說明,爆震波穩定速度均為振蕩平均值.

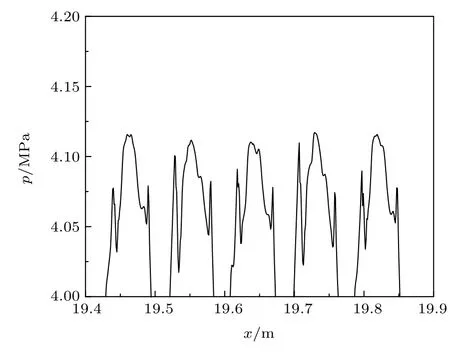
圖2不同時刻爆震波壓力峰附近的壓力分布Fig.2.Pressure distribution near peak at different time.

楊晉朝等[29]提出了一種基于粉末沖壓發動機燃燒室環境的鎂顆粒點火燃燒模型,能夠較全面地反應鎂粉塵云的燃燒過程,在低速層流環境下計算結果與試驗符合度較好.在標準參考條件且不考慮側壁面損失和顆粒表面凝結的前提下,分別采用本文鎂顆粒點火燃燒模型與文獻[29]的鎂顆粒點火燃燒模型,獲得爆震波內流場參數分布,如圖3所示.由圖可知,兩種模型計算得到的爆震波結構存在明顯不同,本文模型計算結果與Zhang等[10]、Federov等[30]描述的爆震波結構相符,氣相密度峰值、顆粒相密度峰值以及壓力峰值均位于前導激波下游某處.而采用文獻[29]的鎂顆粒點火燃燒模型得到的爆震波結構與氣相燃料爆震類似,前導激波處的壓力和密度均為峰值.這是由于文獻[29]中的點火燃燒模型認為鎂顆粒在完全熔化之后到沸騰之前這一階段,除了鎂顆粒表面蒸發過程,在顆粒表面還同時發生氧氣與鎂液滴的異相反應,異相反應放熱均被顆粒吸收,模型中鎂液滴與氧氣異相反應的速率比熔化前固體鎂與氧氣的異相反應高出至少3個量級.由圖3(c)中模型的顆粒相溫度曲線可知,前導激波后顆粒溫度迅速升高達到沸點,幾乎看不到顆粒熔化過程.與之相比,本文模型對應的顆粒溫度曲線可以明顯看出前導激波后鎂顆粒歷經的整個“升溫-熔化-升溫-沸騰”過程.

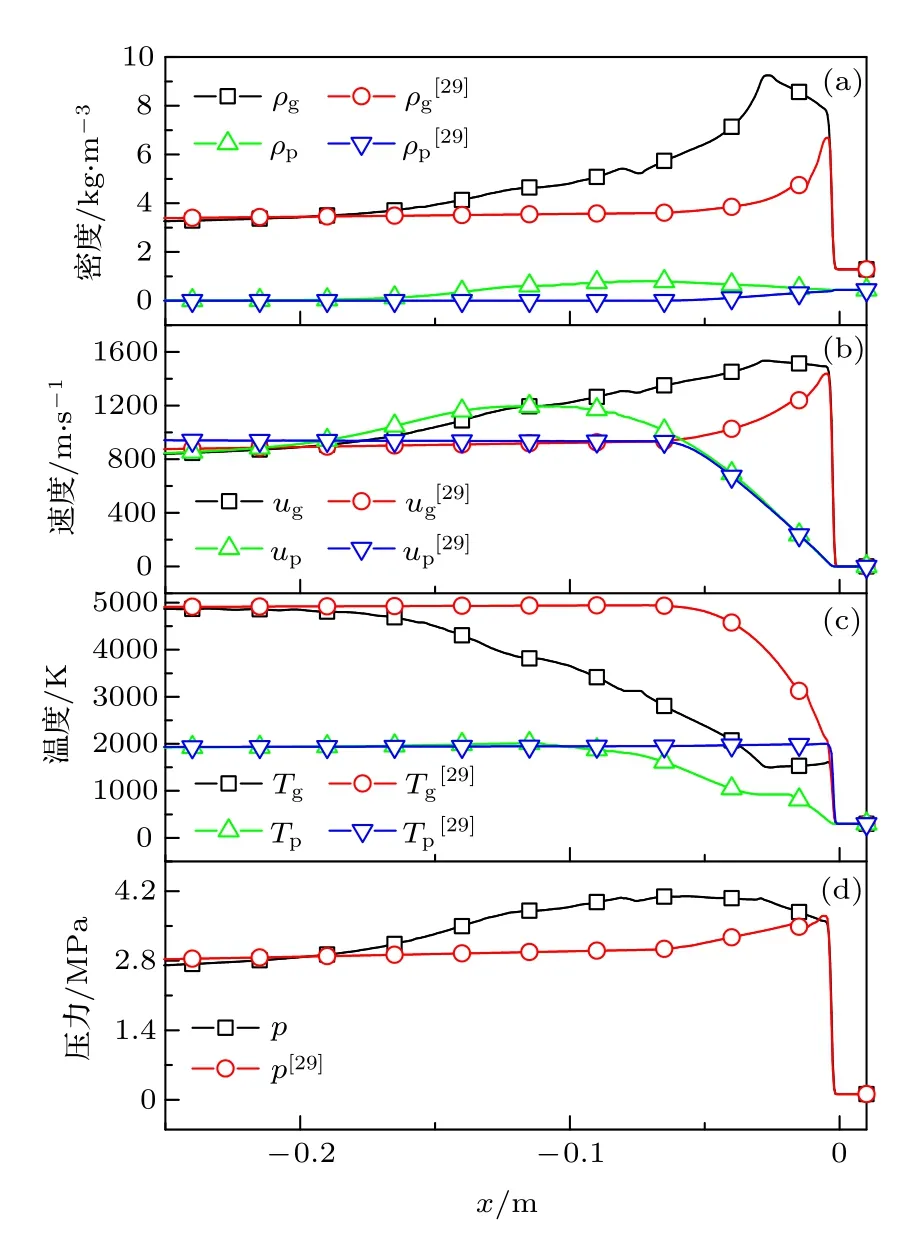
圖3 不同燃燒模型對應的爆震波內流場參數分布(a)密度和濃度;(b)速度;(c)溫度;(d)壓力Fig.3.Parameters distribution in detonation wave with different combustion models:(a)Density and concentration;(b)velocity;(c)temperature;(d)pressure.

采用本文點火燃燒模型模型、文獻[29]中的點火燃燒模型以及文獻[8]中的兩相ZND模型分別計算得到的爆震波穩定傳播速度和爆震波厚度結果如表1所示.由表可知,本文點火燃燒模型計算得到的爆震波速度和厚度與兩相ZND模型基本一致,采用文獻[29]的鎂顆粒點火燃燒模型計算得到的爆震波速度略高,爆震波厚度明顯縮短.基于上述結果可知,相比文獻[29]中的模型,本文模型更加適用于描述前導激波后高溫高壓強迫對流條件下的鎂顆粒燃燒過程.

表 1不同模型對應的爆震波穩定速度和厚度Table 1.Steady velocity and thickness of detonation wave with different models.

3.2 顆粒表面沉積的影響

圖4所示為fS=1.1時對應的穩定傳播狀態爆震波兩相溫度分布.由圖可知,在CJ面上游,由于顆粒相中的液態鎂蒸發持續吸熱,顆粒相溫度維持在鎂的沸點.經過CJ面,下游顆粒相組分僅剩下沉積的氧化鎂,在相間傳熱作用下溫度繼續上升.

圖4 在f S=1.1時對應的穩定傳播狀態爆震波兩相溫度分布Fig.4.Temperature distribution of gas and particle phases inside steady detonation wave withf S=1.1.

圖5所示為爆震波穩定后的爆震波厚度、CJ面兩相溫度、CJ面顆粒相濃度(鎂和氧化鎂沉積)和傳播速度隨fS的變化規律.由圖5(a)可知,爆震波厚度隨fS增加無明顯變化.由圖5(b)和圖5(c)可知,隨著fS的增大,CJ面兩相間溫差和CJ面處沉積濃度均增大,由于單位體積內產物沉積釋放的熱量與沉積濃度和兩相間溫差成正相關,因此產物沉積釋放的熱量隨fS增大而增大.氧化鎂沉積在鎂顆粒表面累積形成球冠狀氧化帽,此過程中釋放的熱量部分被氣態工質吸收用于膨脹做功.由于產物沉積釋放的熱量隨fS增大而增大,因此氣態工質膨脹做功隨fS增加而增加,導致爆震波穩定傳播速度隨fS增大而增大,如圖5(d)所示.在爆震波厚度不變的情況下,爆震波穩定傳播速度升高,鎂顆粒在爆震波內的駐留時間變短.圖5(c)表明CJ面鎂顆粒是完全反應的,因此隨著fS增大,鎂顆粒反應速率整體增大.氧化鎂沉積對于鎂顆粒反應速率的影響:一方面形成的氧化帽減少鎂顆粒表面有效蒸發面積,導致鎂顆粒反應速率降低;另一方面氧化鎂沉積放熱提高了爆震波內的壓力和溫度,促進鎂顆粒蒸發,使鎂顆粒反應速率增大.根據對計算結果的分析可知,沉積放熱對顆粒反應速率的影響占主導作用.因此,模型中考慮氧化鎂的沉積過程,會使鎂顆粒的反應速率增大和爆震波的穩定傳播速度增大.

圖5爆震波參數隨f S的變化(a)爆震波厚度;(b)CJ面兩相溫度;(c)CJ面顆粒相濃度;(d)爆震波速度Fig.5.Variation of detonation parameters with different value of f S:(a)Thickness;(b)temperature at CJ plane;(c)particle concentration at CJ plane;(d)velocity.

3.3 壁面能量損失的影響

根據文獻[8]的研究結論可知,在不考慮外界損失的理想條件下,當且僅當來流速度條件為對應工況的特征值爆震速度時,爆震波結構穩定且在CJ面處鎂顆粒恰好完全反應.當來流速度低于特征值爆震速度時,在波后氣相達到聲速面處仍有顆粒燃料未反應,導致出現奇點,表明對應的爆震波無法穩定傳播.與理想條件相比,引入側壁面損失后,反應釋放的總能量有一部分通過側壁面對流換熱損失,導致可轉化氣態工質膨脹功的能量比例減少,不足以維持爆震波穩定傳播,爆震波傳播速度必然降低.Zhang等[10]在研究鋁顆粒-空氣混合物爆震的模型中考慮了爆震管側壁面損失,其處理方法是在氣相動量方程和氣相能量方程中引入了新的源項,爆震波傳播速度與波后膨脹功之間會達到一個新的平衡狀態,使爆震波能夠以一個低于理想條件ZND特征值爆震速度的速度值穩定傳播,在這種情況下,爆震波CJ面處顆粒燃料未完全反應,這與理想情況下CJ面處顆粒燃料完全反應不同.

表 2不同爆震管內徑條件下爆震波穩定傳播速度、厚度和r CJ/r0Table 2.Steady velocity,thickness and r CJ/r0 at CJ plane of detonation wave with different tube inner-diameters.

由表2可知,隨著爆震管內徑減小,爆震波穩定傳播速度減小, 爆震波厚度減小, CJ面處未反應顆粒所占比例增大.穩定傳播速度增大和CJ面處未反應顆粒比例增大是由于根據方程組(1)中氣相動量方程和氣相能量方程的源項部分,側壁面造成的損失大小與爆震管內徑成反比所致.當管徑為1 m時,管壁引起的損失相對較小,而一些試驗中常用的爆震管管徑尺寸300 mm[31,32]和150 mm[33,34]左右等,管壁造成的損失與理想條件相比已經非常明顯.下文涉及理想條件與考慮爆震管側壁面損失的工況對比時, 無特別說明, 均以管徑0.15 m為參考.

爆震波速度降低,對應波后von Neumann狀態的氣相溫度和壓力降低.圖6(a)和6(b)為不同管徑條件下爆震波內的壓力和氣相溫度分布,為方便對比,將各算例結果對應的前導激波面置于同一坐標位置.由圖可知,隨著內徑減小,爆震波內的壓力和氣相溫度整體降低,但總的分布趨勢不變.隨著壓力和氣相溫度的降低,對應的當地聲速也隨之減小.在兩相CJ模型中,坐標系固定在前導激波上,CJ面對應的是波后氣相達到當地聲速的平面.而在非穩態模型,由于參考系的轉換,CJ面對應的是波后氣相與前導激波間的相對速度達到當地聲速的平面.由于側壁面摩擦對波后氣相有一個減速作用,使得波后氣相與前導激波之間的相對速度能夠更快地達到當地聲速,因此隨著爆震管內徑減小,爆震波厚度減小.

3.4 顆粒初始粒徑的影響

表3給出了在不同顆粒初始粒徑條件下,理想條件和管徑為0.15 m時爆震波傳播速度和厚度的計算結果.根據表3可知,在不考慮壁面損失的理想條件下,爆震波穩定傳播速度隨粒徑增大仍然保持不變,爆震波厚度隨粒徑增大而增大,這與文獻[8]得到的結論一致.這是由于理想條件下在CJ面處鎂顆粒完全反應,反應釋放的總能量相同,因此爆震波穩定速度保持不變,而在鎂顆粒初始質量相同的前提下,初始粒徑增加導致顆粒反應/蒸發表面積減大,波后氣相膨脹過程變緩,最終導致爆震波厚度增加.

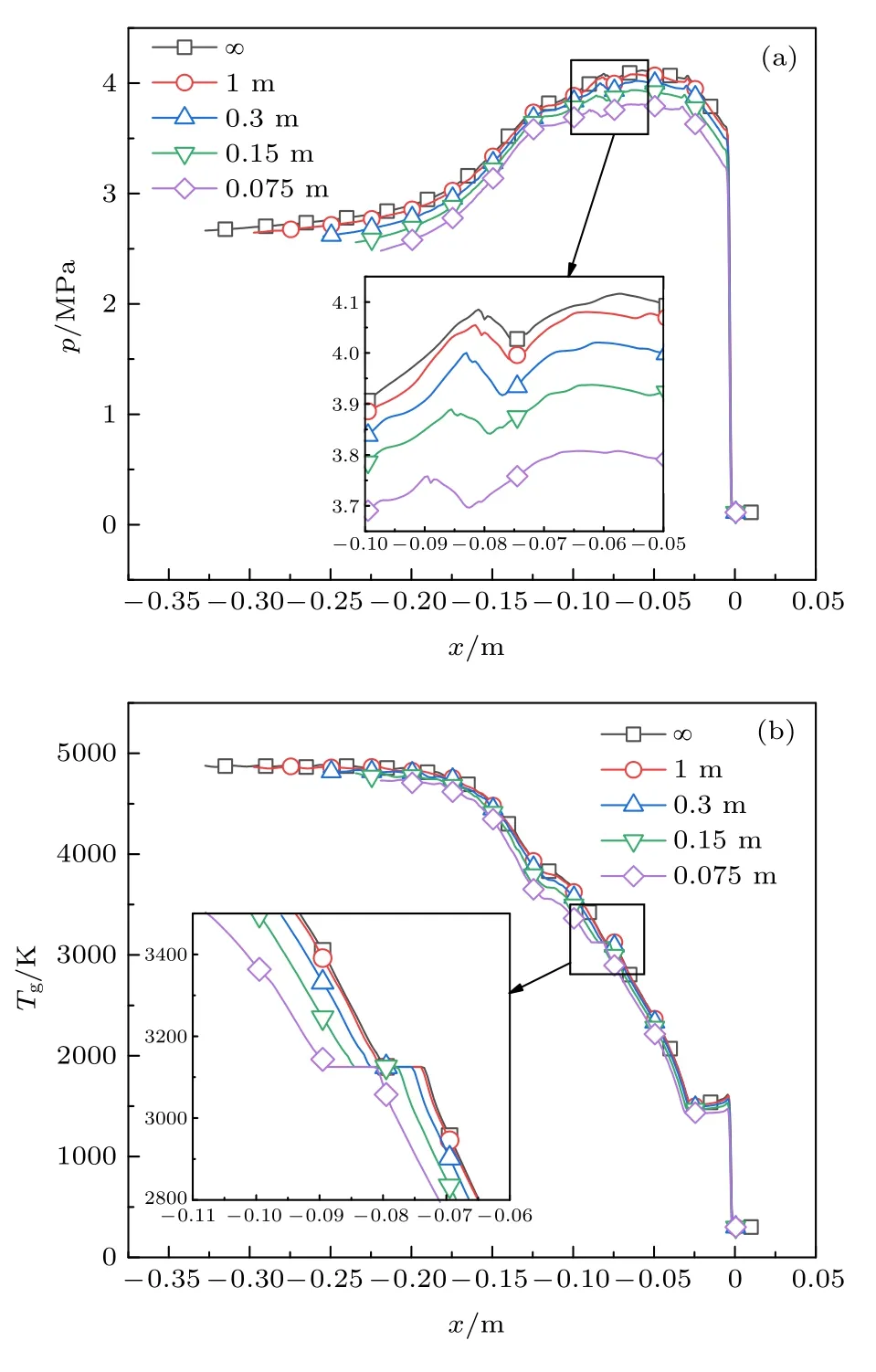
圖6不同管徑條件下爆震波內的壓力和氣相溫度分布(a)壓力;(b)氣相溫度Fig.6.Pressure and gas-phase temperature distribution inside detonation wave with different tube inner-diameters:(a)Pressure;(b)gas-phase temperature.

表3不同顆粒初始粒徑對應的爆震波傳播速度和厚度Table 3.Steady velocity and thickness of detonation wave with different initial particle diameter.

而在考慮壁面損失的條件下,隨著顆粒初始粒徑的增大,爆震波穩定速度與理想條件下的差值也隨之增大,這是由于側壁面造成的換熱損失與爆震波厚度呈正相關關系,爆震波厚度越大,對應的換熱面積就越大,爆震波內反應釋放的總能量損失也越多,爆震波穩定傳播速度與理想條件下的差值也越大.同時,由表3可知,與理想條件下相比,爆震波厚度的減小量也隨顆粒初始粒徑的增大而增大.這是由于爆震波所受壁面總黏性力的大小與爆震波厚度呈正相關關系,爆震波厚度越大,爆震波整體所受壁面總黏性力就越大,根據3.3節的分析,壁面黏性力能夠使波后氣相與前導激波之間的相對速度達到當地聲速的過程加快,因此爆震波厚度的減少量也會隨壁面總黏性力的增大而增大.綜上所述,在考慮爆震管側壁面損失的情況下,隨著粒徑增大,爆震波穩定傳播速度和爆震波厚度與理想條件下的差值也增大.

此外, 表3還給出了平均初始粒徑為10 μm(5 μm和15μm的鎂顆粒按質量比1:10均勻混合)的計算結果,可以看出,與初始粒徑統一為10μm的工況相比,雙粒徑分布對應的理想條件下爆震波穩定狀態厚度明顯增高, 甚至高于初始統一粒徑為15μm工況的厚度,這是因為在雙粒徑分布的爆震波內,小粒徑鎂顆粒很快被完全消耗, 剩余的大粒徑15μm顆粒,顆粒數目較少,反應表面積較少,因而反應速率更低,導致波后氣相膨脹至與前導激波相對速度為當地聲速需要的時間更長,爆震波的厚度更大.在考慮壁面損失的條件下,雙粒徑分布對應的爆震波速度明顯低于統一粒徑的工況.對于實際鎂粉顆粒可以而言,其粒徑存在一個分布范圍,因此可以推測實際鎂粉爆震試驗得到的爆震波速度值可能低于按照平均粒徑計算得到的爆震波速度值.

3.5 初始當量比的影響

圖7為理想條件和管徑為0.15 m條件下,穩定傳播的爆震波速度和爆震波厚度隨初始當量比的變化.根據圖7(a),在理想條件下,隨著鎂顆粒-空氣當量比增大,爆震波穩定傳播速度先增大后減小,速度最大值對應的當量比略小于1, 這與文獻[8]中的結論一致.根據圖7(b),在理想條件下,爆震波厚度隨當量比增加先減小后增大,是因為在當量比小于1時,隨著當量比增大,爆震波內顆粒反應面積增大,反應速率增大,放熱率增大,氣相工質吸熱膨脹速率增大,波后氣相與前導激波間的速度差達到當地聲速所需時間更短,因此爆震波厚度減小.當量比大于1時,在貧氧條件下,未燃燒部分的鎂顆粒吸熱蒸發產生與鎂沸點溫度相同的蒸氣,使氣相溫度整體降低,氣相實際膨脹做功速率減小.隨著初始當量比增大,鎂顆粒蒸發面積隨之增大,蒸發速率隨之增大,實際氣相膨脹做功速率隨之減小,波后氣相與前導激波間的速度差達到當地聲速所需時間更長,因此爆震波厚度增大.

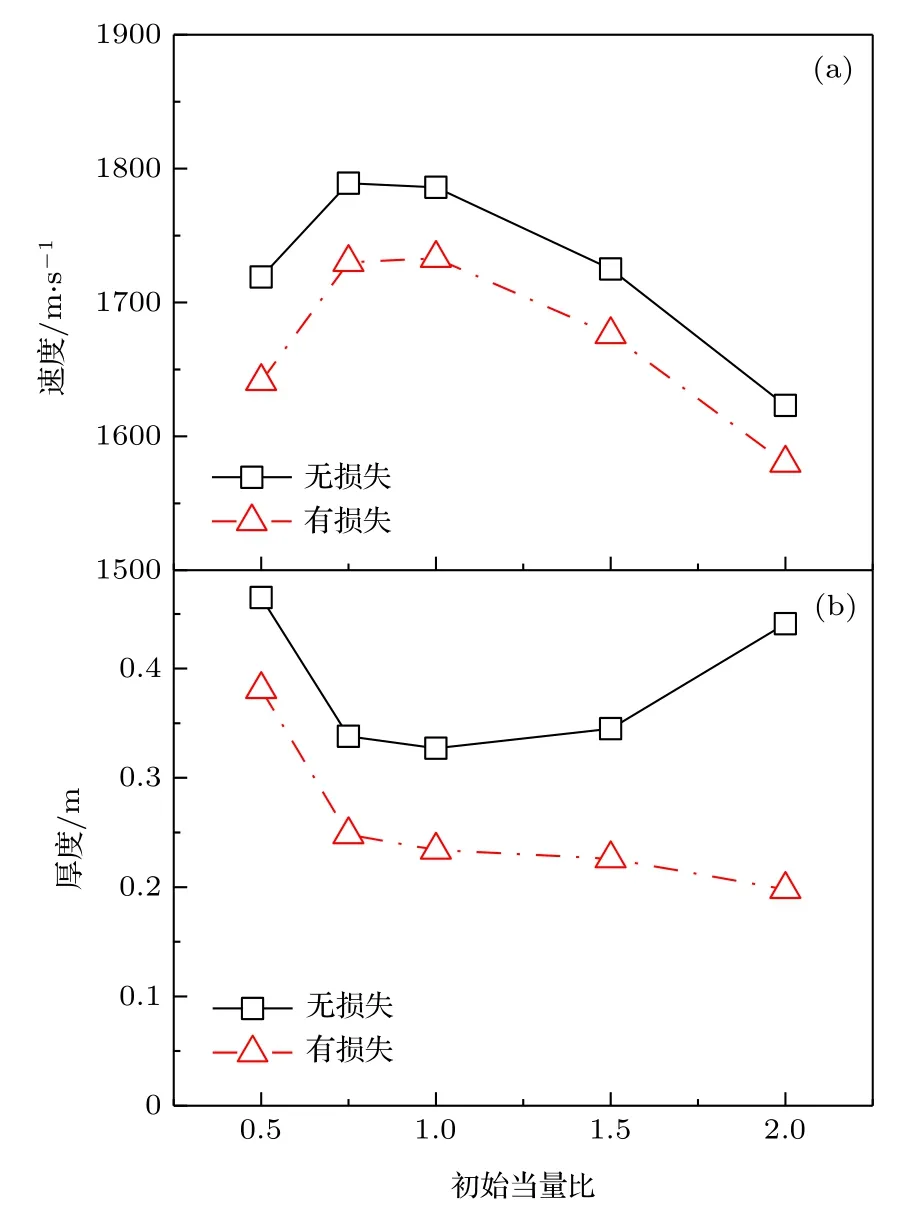
圖7穩定傳播的爆震波速度和爆震波厚度隨初始當量比的變化(a)速度;(b)厚度Fig.7.Variation of steady velocity and thickness of detonation wave with different initial equivalent ratio:(a)Velocity;(b)thickness.

在考慮管壁損失的條件下,爆震波穩定速度隨初始當量比的變化趨勢與理想條件一致,穩定傳播速度與理想條件下的差值隨當量比增大略有減小,一方面是由于爆震波厚度隨當量比增大而降低,側壁面換熱面積隨之減小,另一方面是由于隨著當量比增加,貧氧工況下剩余的鎂顆粒吸熱增多,氣相與側壁面間的溫差減小,上述兩方面的原因共同導致側壁面換熱損失降低.爆震波厚度隨初始當量比的變化趨勢與理想條件時不同,初始當量比大于1的條件下,爆震波厚度隨初始當量比的增大仍然繼續減小,與理想條件爆震波厚度的差距進一步拉大.如圖8所示為初始當量比分別為1.0、1.5和2.0時,在理想條件下和有壁面能量損失的條件下爆震波內氣相密度分布.由圖可知,氣相密度整體隨初始當量比增大而增大,且在爆震波首段和末段差別明顯.這是由于在首段,兩相間速度差較大,顆粒相對氣相的壓縮作用隨初始當量比增大而增強;在中段,兩相速度趨于一致,壓縮作用明顯減弱;在末段,未反應鎂蒸氣的含量隨著初始當量比的增加,導致氣相密度隨初始當量比的增大而增大.根據壁面黏性摩擦力公式(17),壁面與氣相間摩擦力大小與氣相密度呈正比,因此氣相所受黏性力隨當量比增大而增大,導致爆震波厚度與理想條件爆震波厚度的差距隨初始當量比的增大而增大.

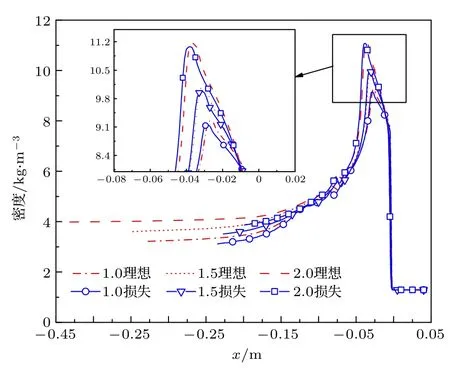
圖8不同當量比條件下爆震波內氣相密度分布Fig.8.Gas-phase density distribution inside detonation wave with different initial equivalent ratio.

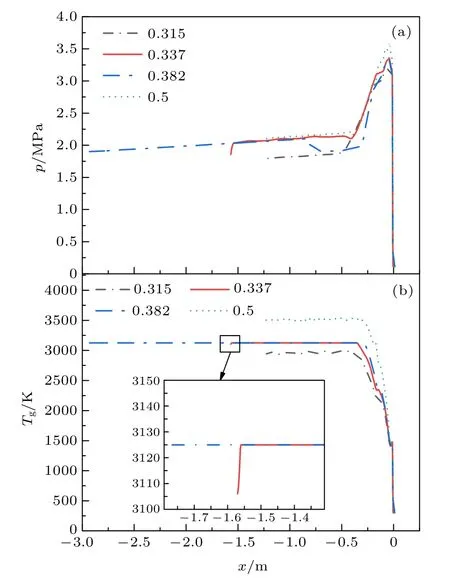
圖9不同初始當量比條件下爆震波內參數分布(a)壓力;(b)溫度Fig.9.Parameters distribution inside detonation wave with different initial equivalent ratio:(a)Pressure;(b)temperature.

文獻[8]中兩相ZND模型的計算結果表明,在一個鎂顆粒初始濃度較低的小范圍內(0.146—0.168 kg/m3),由于產物MgO的熔化過程發生在氣相相對前導激波的相對速度即將達到聲速的階段,熔化吸熱導致氣相膨脹過程受到影響無法加速,因而對應的爆震波無法以一個穩定的速度傳播,而可能是以某一速度為均值而進行振蕩傳播.而本文的非穩態模型計算結果表明,爆震波在傳播過程中自身伴隨著小幅振蕩.為進一步研究上述發生在臨近爆震波末端的MgO熔化過程對爆震波傳播穩定性和結構的影響,以理想條件下初始當量比分別為0.315、0.337、0.382和0.5(對應鎂顆粒初始濃度分別為0.14 kg/m3、0.15 kg/m3、0.17 kg/m3和0.222 5 kg/m3)的工況為例,圖9為不同初始當量比條件下充分發展后的爆震波內壓力和氣相溫度分布.由圖9可知,初始當量比為0.315對應的工況氣相壓力始終低于MgO熔點(3125 K),表明此工況下爆震波內MgO未發生熔化;初始當量比為0.5對應的工況在爆震波末端氣相溫度明顯高于MgO熔點,表明此工況下爆震波內MgO已完全熔化;初始當量比為0.337對應的工況在爆震波內氣相溫度先升高達到MgO熔點后,在爆震波末端氣相溫度又降至MgO熔點以下,表明此工況下爆震波內MgO經歷先部分熔化后又重新凝固的過程,并且氣相溫度下降段對應的壓力明顯降低,此過程中氣相繼續膨脹做功直至其與前導激波相對速度達到當地聲速;初始當量比為0.382對應的工況在爆震波內氣相溫度升高至MgO熔點后不再變化,表明此工況下爆震波末端MgO始終處于熔化過程中,根據壓力分布可知,在前導激波面下游約0.75 m處,氣態工質停止膨脹,壓力明顯回升,表明此工況下充分發展后的爆震波內的氣態工質出現一個強度相對較低的二次壓縮過程.此外,由圖9還可以看出,初始當量比為0.315和0.5時對應的爆震厚度大致相等,而初始當量比為0.337和0.382時,爆震波厚度顯著增大,表明發生在臨近爆震波末端的MgO熔化過程使爆震波厚度顯著增加.圖10為爆震波趨于穩定傳播狀態時在不同位置處的對應的爆震波壓力峰值,取樣時間間隔為0.1 ms.由圖可知,不同初始當量比條件下爆震波壓力峰值均存在振蕩,且振幅大致相等,約為0.05 MPa,表明發生在臨近爆震波末端的MgO熔化過程對爆震波傳播穩定性的影響基本可以忽略不計.

圖10不同初始當量比條件下不同位置處的爆震波壓力峰值Fig.10.Pressure peak at different position with different initial equivalent ratio.

3.6 初始點火條件的影響

根據標準參考工況條件下穩定傳播的爆震波速度1786 m/s計算得到對應的正激波波后參數作為點火區的流場初值,點火區大小分別取1倍、0.5倍、0.25倍和0.125倍穩定爆震波厚度,得到沖擊波誘導起爆條件下的前導激波面在發展成為穩定傳播過程中的速度變化,如圖11所示.點火區長度為0.125倍穩定爆震波厚度的情況,爆震波起爆失敗,故其結果未在圖中顯示.由圖可知,點火區長度為1倍和0.5倍爆震波厚度時,前導激波在經過開始的一小段加速過程(分別對應2.319—2.83 m和2.017—2.315 m)后,開始逐漸衰減直至達到穩定傳播狀態.而當點火區長度為爆震波厚度的0.25倍時,前導激波先是衰減,速度降至穩定傳播速度以下,當速度降至1237 m/s時,爆震波停止衰減,并開始逐漸加速達到過驅爆震狀態,速度達到1953 m/s后,前導激波開始逐漸衰減直至達到穩定傳播狀態.開始的衰減是由于點火區較短,初始膨脹波強度較大導致的.當點火區厚度較大時,初始膨脹波強度較弱,對前導激波的削弱作用較小.

圖11不同點火區長度對應的爆震波速度發展過程Fig.11.Development of detonation wave velocity with different length of ignition zone.

當點火區大小為1倍穩定厚度,點火區流場參數初值分別為0.8倍、1.0倍和1.2倍爆震波穩定速度正激波后的von Neumann參數時,計算得到前導激波面在發展成為穩定傳播過程中的速度變化,如圖12所示.1.2倍穩定速度的結果與1.0倍的趨勢一致,定量關系上其對應的前導激波速度更高.0.8倍穩定速度的結果與另外兩者明顯不同,是直接加速直至爆震波達到過驅狀態,再漸進衰減至穩定速度.參考氣相爆震沖擊波起爆的研究結果[21],對于點火區的沖擊波總能量,存在起爆界限(下限)和過驅界限(上限).對于鎂顆粒-空氣混合物而言,當沖擊波總能量高于上限時,在爆震波發展至穩定傳播過程中,前導激波速度始終高于穩定速度(如圖11中的曲線1.0和0.5以及圖12中的曲線1.0和1.2).當沖擊波總能量低于下限時,爆震波無法起爆.在點火條件處于上限和下限之間,則前導激波會經歷速度衰減至穩定值以下,而后爆震波加速至過驅狀態(前導激波速度高于穩定速度),再逐漸達到穩定速度的過程.

圖12不同點火區參數對應的爆震波速度發展過程Fig.12.Development of detonation wave velocity with different field parameters of ignition zone.

綜合以上計算結果可以看出,點火區參數對爆震波最終的穩定傳播狀態沒有影響,但會影響爆震波發展過程.點火區參數和長度滿足一定條件(如點火區長度為0.5倍穩定厚度,流場參數為穩定波速對應的正激波后von Neumann參數),能夠使爆震波發展至穩定狀態所傳播的距離明顯縮短.這對于采用沖擊波起爆方式的連續旋轉爆震發動機盡快實現爆震波在燃燒室內的穩定傳播具有重要指導意義.

4 結 論

本文針對鎂顆粒-空氣混合物爆震建立了一維非穩態模型,通過數值模擬不同工況下的爆震波非穩態自維持傳播過程,獲得了爆震波內流場參數的分布以及爆震管側壁面損失、鎂顆粒半徑、鎂顆粒初始當量比、顆粒表面沉積過程以及點火能量對爆震波結構和發展過程的影響規律.研究表明,充分發展后的鎂顆粒-空氣混合物一維非穩態爆震波在傳播過程中存在振蕩現象, 但振幅較小,在 ±1 m/s以內;在考慮燃燒產物在顆粒表面沉積的情況下,顆粒反應速率和爆震波穩定速度均隨燃燒產物在顆粒表面的凝結速率的增大而增大,對應的爆震波厚度基本保持不變.

在考慮爆震管側壁面損失的條件下,隨著管徑減小,爆震波內的壓力與溫度均降低,進而導致爆震波傳播速度和爆震波厚度減小;在不考慮管壁損失的理想條件下,隨著顆粒初始粒徑增大,爆震波穩定速度保持不變,爆震波厚度單調遞增.考慮管壁損失時,得到的爆震波穩定速度和厚度均低于同等初始條件下理想工況的結果,且由于管壁造成的損失與爆震波厚度成正相關,因此考慮損失和理想條件下爆震波速度和厚度的差值均隨顆粒初始粒徑的增大而增大;初始粒徑為雙粒徑分布的工況(5μm和15μm混合)與對應的初始單一粒徑分布(10μm)的工況相比,小粒徑鎂顆粒很快被完全消耗,剩余的大粒徑顆粒數目較少,反應表面積較少,導致爆震波的厚度更大,且在考慮壁面損失的條件下,雙粒徑分布對應的爆震波速度明顯低于統一粒徑的工況.對于試驗用鎂顆粒而言,其粒徑存在一個分布范圍,因此可以推測鎂粉爆震試驗得到的爆震波速度值可能低于按照平均粒徑計算得到的爆震波速度值.

在顆粒初始當量比0.5—2范圍內,隨初始當量比增大,不考慮壁面損失的條件下爆震波穩定速度先增大后減小,爆震波厚度先減小后增大.在考慮壁面損失的條件下,隨著初始當量比增大,穩定爆震波速度先降低后增大,由于爆震波內氣相密度隨當量比增大而單調增大,因此爆震波厚度隨初始當量比增加而單調遞減;當初始顆粒初始當量比在一個較低范圍內(0.337—0.382),滿足MgO熔化發生在CJ平面附近時,MgO熔化過程對爆震波傳播穩定性無明顯影響,而對爆震波結構影響較大:初始當量比偏低的情況下,爆震波內MgO先部分熔化而后重新凝固,CJ面處的MgO為固態;初始當量比偏高的情況下,CJ面處MgO仍處于熔化過程中,且爆震波內存在一個強度較低的二次壓縮過程.

點火區參數對爆震波最終的穩定傳播狀態沒有影響,但會影響爆震波發展過程:當點火區能量高于上限時,爆震波在發展至穩定傳播過程中,前導激波速度始終高于穩定速度;當低于下限時,爆震波無法起爆;點火能量在上限和下限之間時,前導激波會經歷速度衰減至穩定值以下,而后爆震波加速至過驅狀態,再逐漸達到穩定速度的過程.合理設置點火條件,可使得爆震波發展至穩定狀態所傳播的距離明顯縮短.這對于采用沖擊波起爆方式的連續旋轉爆震發動機盡快實現爆震波在燃燒室內的穩定傳播具有重要指導意義.

本模型較全面地反映出管壁損失、顆粒初始粒徑、顆粒初始當量比、顆粒表面沉積以及點火區參數對爆震波非穩態傳播過程的影響,對采用粉末燃料的爆震動力裝置設計具有一定的指導意義.基于本文的工作,下一步可開展鎂顆粒-空氣混合物二維連續旋轉爆震燃燒數值模擬的相關研究.