基于Wiener 模型的非線性系統的魯棒預測控制

封曉宇 張冬雯

（1、河北科技大學電氣工程學院，河北 石家莊050018 2、河北科技大學信息科學與工程學院，河北 石家莊050018）

預測控制是從工業控制過程中興起的一種新型計算機控制方法。因為預測控制的應用價值較高且應用范圍的較為廣闊，所以在控制領域預測控制成為熱門研究的對象[1-4]。

在實際生產過程中，非線性系統普遍存在且研究較多的，正是由于該原因，所以針對非線性系統預測控制目前已有很多研究成果[5]。文獻[6]針對一類非線性不確定系統，根據時滯和不確定性選擇了相關的李雅普諾夫函數，通過線性矩陣不等式和變量變換對設定的二次函數性能指標的最小值進行了求解，得到閉環系統穩定性的充分條件。

Wiener 模型之所以能夠在工業過程中得以廣泛應用，是因為其能很好的描述一大類非線性對象。文獻[7] 提出了基于Wiener 模型的改進式非線性預測控制算法。Laguerre 級數展開式描述Wiener 模型的線性部分，在Wiener 模型的非線性部分利用靜態模糊模型進行描述，此時的非線性系統則可采用線性預測控制的方法求解預測控制律，避免了直接對非線性系統進行優化求解。

本文針對一類Wiener 模型描述的非線性時滯系統，研究了Wiener 模型的預測控制問題。采用Lyapunov-Krasovskii 函數設計了每個子系統的狀態反饋控制律，在"min-max"的性能指標下，求解了優化問題，得到了系統漸近穩定且具有較小保守性的充分條件。

1 問題描述

考慮如下離散狀態空間模型描述的非線性時滯系統：

其中，x（k）∈Rn為狀態向量，u（k）∈Rm為輸入向量，y（k）∈Rq為輸出向量，d 為時滯常數。

通過Wiener 模型來近似描述非線性時滯離散系統（1）。其中Wiener 模型是由一個線性單元與一個非線性單元串聯組成，動態線性單元由狀態方程描述，靜態非線性部分由T-S 模糊模型進行線性逼近。非線性時滯離散系統（1）可以被分割成j（j=1，…，L）個局部子系統，每一個子系統的模型用以下模糊模型表示：

在規則Rj下

IF z1（k）is Vj1，zg（k）is Vjg

THEN

其中A，B，Ad，C 為具有適當維數的已知常數陣，Z（k）=[z1（k）…zg（k）]T為前件變量，j∈（1，…，L），L 為模糊規則數，Vjα（α=1，…，g）為模糊合集；?j和σj0分別為在j 條規則下常數矩陣，ΔA，ΔB，ΔAd表示具有適當維數的不確定時變矩陣，假設不確定性時變矩陣是范數有界的，且具有以下形式：

其中，H，Ea（a=1，2，3）表述具有適當維數的已知常數陣，F（k）是時變矩陣，表示模型的不確定性，且滿足FTF（K）≤I，其中I 表述具有適當維數的單位矩陣。

通過采用平均加權反模糊化，非線性時滯離散系統（1）最終可以表示為：

考慮無限時域的魯棒預測控制，設滾動優化的性能指標為：

其中，Q＞0，R＞0 均為已知對稱正定權矩陣。最優問題（5）是一個min-max 問題，表示所有可能的使得性能指標取最壞情況下所有可能的不確定矩陣以及使最小化最差性能指標時的輸入問題。

第j 條規則下的控制律為u（k+i）=Kjx（k+i），其中Kj為第j條規則下相應的狀態反饋增益。

非線性時滯離散系統（1）的控制目標是在每個采樣周期內，通過求解優化問題（5），得到非線性時滯離散系統（1）的模糊控制律u（k+i）=Kμx（k+i）。

為能夠得出結論，首先列出如下引理：

引理1：給定適當維數的矩陣G1，G2和對稱矩陣Ω，對所有滿足FT（t）F（t）≤I 的矩陣F（t），有

Ω+G1F（t）G2+G2TFT（t）G1T＜0

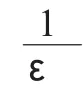
2 非線性預測控制器設計與算法

在每一采樣周期，為了得到無限時域性能指標的上確界，采用了一個不等式條件，這時無限時域的優化問題，就轉化為最小化上確界的最壞情況的求解問題，即“min-max”問題。然后通過利用線性矩陣不等式來給出狀態反饋模糊控制器的表達式。

非線性時滯離散系統（1）是由L 個子系統加權反模糊所得，故當每個子系統都能使優化問題（5）有解，那么整個非線性時滯離散系統的優化問題必然有解。

針對非線性時滯離散系統（1），在每個子系統均采用如下Lyapunov-Krasovskii 函數：

其中Pj＞0，S＞0。

為保證非線性時滯系統的魯棒穩定性，在每個子系統的采樣周期內對于所有可能的不確定時變矩陣和控制律，要求Lyapunov-Krasovskii 函數滿足下列約束：

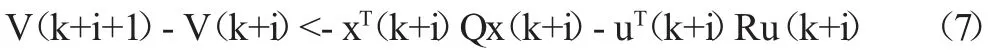
要使無限時域性能指標有界，則應滿足收斂性，對式（7）從i=0 到i=∞進行求和，此時可以得到無限時域性能指標的上界，且無限時域性能指標的最壞情況轉化為

故“min-max”問題則轉化為求解式（8）最小化的解。

定理：考慮時滯非線性離散系統（1），假設x（k）為采樣時間k 的測量狀態，若各子系統存在正定矩陣Tj＞0，Yj，W 以及標量γ＞0，ε＞0，使得如下線性矩陣不等式有可行解：

則對于由式（2）和各子系統的控制律組成的子閉環系統漸近穩定，并最小化性能指標的最壞上界。且子系統的控制器的增益為Kj=YjTj-1（j=1，…，L）。

令Tj=γPj-1，W=γS-1帶入式（6），并利用Schur 補引理可得式（9）。

3 仿真實例

為證明上述方案的可行性，采用由Wiener 模型描述的連續攪拌釜式反應器的放熱反應過程進行仿真驗證。反應器體積為V=100l，進料流量為F=100l/min，反應溫度為T=438.54，活化能E/R=1×104，進料濃度CAf=1mol，反應率常數K0=7.2×1010，熱傳遞系數hA=7×105cal/（min·K），冷入口溫度Tc=350K，進料溫度Tf=350K，密度ρ=1×103g/l。通過辨識，采用MATLAB 軟件進行仿真，仿真結果如圖1 所示，可以看出該算法能夠使得輸出穩定至穩定點。

圖1 反應物濃度曲線

4 結論

本文以一類Wiener 模型描述的非線性系統為研究對象，結合預測控制原理與模糊理論，研究了基于線性矩陣不等式的預測控制器算法設計問題，利用Lyapunov 函數設計了狀態反饋控制律，推導出了閉環系統漸近穩定和性能指標最優化的充分條件，減少計算量，得到較小保守性。