S 方法抑制交叉項原理分析及其應用

吳凌華 張 曦 周 新

（1、海軍裝備部，四川 成都610000 2、空軍工程大學，陜西 西安710000 3、空裝駐成都地區第三軍代室，四川 成都610000）

1 概述

時頻分析方法通過將一維時域信號映射到能量對時間頻率二維的分布上，有效地表征了信號的時頻域聯合特征，是非平穩信號分析的有力工具。時頻分析方法主要分為兩類：線性時頻分析方法和雙線性時頻分析方法[1]。

短時傅立葉變換是線性時頻分析方法中的典型代表，盡管其時頻聚焦性能不好，但其算法簡單高效，且不存在交叉項干擾。WVD分布是一種典型的雙線性時頻分析方法，其分布結果有著非常直觀的物理意義[2]。雖然其具有較好的時頻聚焦性能，但存在嚴重的交叉項干擾。尤其在多分量信號的時侯，交叉項的出現往往掩蓋了信號項，難以準確辨認信號的時頻分布規律。考慮到短時傅立葉變換無交叉項干擾，而WVD 分布時頻聚焦性好，結合這兩種方法找到兼顧其優點的時頻分析方法是一種提高時頻分析性能的思路，基于此Stankovic L等人提出了S方法的時頻分析方法[3]。該方法綜合了譜圖和WVD 的優點，在保持高時頻分辨、力的同時能夠有效抑制交叉項，算法復雜度低，在多分量信號分析中得到了廣泛應用[4-12]。

本文根據S方法的定義，重點研究了其抑制交叉項的原理，并以此為基礎對S方法的實現算法進行了詳細分析，然后利用仿真得到其結果，通過對比分析驗證了S方法的有效性。

2 S 方法的時頻分析原理

2.1 S方法的定義。回顧短時傅立葉變換的定義：

其中，w（τ）是加權窗，窗寬為T。

Wigner 分布最早是由諾貝爾物理學獎獲得者Wigner 于1932年在量子力學中引入的，信號s（t）的Wigner 分布（WD）定義為[1]：

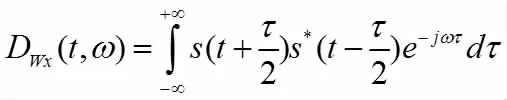
Ville 于1948 年采用信號的解析形式x（t）代替s（t），將Wigner分布重新定義為：

稱為Wigner-Ville 分布。WVD 分布本質上是一種雙線性變換，雙線性破壞了線性疊加原理。多分量信號的情況下，WVD分布中每兩個分量都會產生相應的交叉項成分，嚴重影響了該分布的使用。

改造WVD分布的最簡單的方法是對變量加窗函數h（τ）來實現減小交叉項的目的。對該方法改造后的WVD 分布稱為偽Wigner-Ville 分布（PWVD），定義為：

其中窗函數w（τ）。

由式（1）和（3），可推出STFT與PWVD的關系：

引入窄窗函數ψ（θ），對式（4）加窗后積分，即得：

這種新的時頻分布稱為S方法[3]。

經變量置換后，上式可寫為：

選擇不同的窗函數ψ（θ）將得到不同的時頻分布，特別有：

（1）當取ψ（θ）=2πδ（θ）時，有：DSM（t，ω）=|SSTFTx（t，ω）|2=SSPECx（t，ω）。（2）當取ψ（θ）=1 時，有：DSM（t，ω）=DPWVx（t，ω）。

雖然（6）式的S方法可以理解為修正的平滑偽Wigner-Ville分布，但它兼顧了短時傅立葉變換和偽Wigner-Ville 分布的優點，有許多優良的特性。

2.2 抑制交叉項原理。多分量間的交叉項干擾是WVD分布的主要困難。S方法能夠有效消除信號分量間的交叉項干擾。下面對其抑制交叉項的原理進行分析。

考慮多分量信號

其中，信號分量si（t）=A（t）ejφ（t）是幅值緩變信號，即|A'（t）|＜＜|φ'（t）|。由于S方法是以短時傅立葉變換為基礎的，故對信號s（t）作短時傅立葉變換。將信號s（t）的相位φi（t+τ）展開成泰勒級數。假設窗內幅值Ai（t+τ）的變化可以忽略，即Ai（t+τ）w（τ）?Ai（t）w（τ），則有：

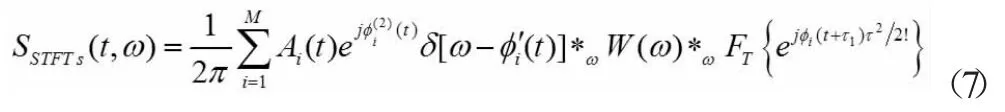
其中，FT[·]是傅立葉變換算子，W（ω）=FT[w（t）]，τ1是[0，τ/2]間隔內的變量，*ω 是頻域卷積。

假設窗內的φi（t+τ1）可忽略，可得到譜圖

設W（ω）的主瓣寬度為WB。令|ω|≥WB/2 時，W（ω）=0。則存在兩種情況：

（1）若給定時間t，對于所有i，j，滿足min[|φ'i（t）-φ'j（t）|]＞WB，則信號的能量僅集中在各分量頻率上；（2）若對于任意的l 和k，[|φ'l（t）-φ'k（t）|]＜WB，則在瞬時頻率φ'l（t）和φ'k（t）之間存在交叉項Al（t）ejφl（t）和Ak（t）ejφk（t）。

由式（4）和式（8），可得到：

若式（9）中雙重求和項非零，須滿足條件：

將兩個不等式相加，則有

下面分析（9）式中交叉項成分在θ 軸的位置。將（10）式和（11）式相減，則有：

則加窗積分后，（5）式完全包括信號自項，且第i 和第j 個成分間的交叉項被消除。

3 實現算法分析

短時傅立葉變換方法雖然受限于不確定原理，時頻分辨率不高，但因其只需要按采樣理論采樣，算法簡單高效，在實際系統中被廣泛應用；Cohen 類時頻分布方法可以有效地抑制WVD 分布中的交叉項干擾，但通常要求2 倍的過采樣，且算法復雜，計算量大，使其應用范圍受限，特別是對于實時性要求較高的系統。S方法則無需過采樣，且其離散化形式可通過高效的遞歸算法求得。

為避免混疊WVD 分布要求以2 倍采樣理論定義的采樣間隔對信號過采樣，或者使用信號的解析形式。S方法不需要對信號過采樣，可以同消除交叉項一樣將混疊部分去除。

考慮對連續信號x（t）以采樣間隔Ts采樣，則采樣后的離散形式為：

其傅立葉變換是沿頻率軸以ωs為周期的周期函數

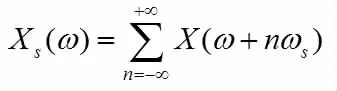
故可將xs（t）作為有無窮分量的連續多分量信號。則對于幅值緩變信號：x（t）=A（t）ejφ（t）

其短時傅立葉變換為：

考慮由（4）式與Wigner-Ville 分布的關系，則可得離散信號的WVD分布形式：

同前述S方法的交叉項分析一樣，當滿足條件：

式（16）中被積函數不為零。積分后信號自項（n1=n2）在θ 坐標系的原點附近。沿θ 軸最近的混疊是n1-n2=±1。當窗函數ψ（θ）滿足：

這些混疊將被消除。與移除交叉項的條件式（13）相比，這個條件是比較寬松的。因此S方法中移除交叉項的條件通常保證了混疊成分的消除。

通過上述分析，可知S方法能夠有效地消除WVD分布中的交叉項干擾，并且不需要對信號過采樣，其離散化形式可采用遞歸算法求得，利于數字信號處理系統高效實現。

4 仿真實例

為驗證S方法時頻分析的有效性，下面通過仿真與典型時頻分析方法進行比較。為簡化仿真，仿真中采用兩個信號之和，一個是載頻f1=11.25MHz的定頻信號，另一個是線性調頻信號起始頻率f2s=375MHz，截止頻率f2e=10.0MHz，采樣頻率為fs=25MHz，時間為T=40.96us，觀測時間內采樣1024 個點，計算時S 方法時間窗選擇長度為128 點的漢寧窗。

5 結論

為了能有效地抑制時頻分布中交叉項的影響，結合短時傅立葉變換和WVD分布兩種方法提出的S方法兼顧了兩者的優點。本文根據S方法的定義，詳細分析了該方法抑制交叉項的原理，并在此基礎上對S方法的實現算法進行了研究，然后利用仿真分析對該方法的有效性進行了驗證：理論分析和仿真實例證明S 方法能夠有效的抑制交叉項的影響，適用于多分量非平穩信號的分析。