基于ADAMS折疊式動臂工作裝置動態特性仿真分析

李兆安

（遵義職業技術學院，貴州 遵義 563000）

折疊式動臂挖掘機工作裝置采用新型的折疊式動臂結構，由后動臂、前動臂、斗桿和鏟斗組合而成。將原先經典的整體式動臂拆分成由前動臂和后動臂兩個結構件鉸接而成的結構，前動臂由兩個前動臂油缸進行調控，后動臂由后動臂油缸（調整油缸）進行調控。在以往的輪式折疊動臂液壓挖掘機設計中，對折疊動臂工作裝置的設計多采用靜力學分析計算來確定工作裝置的受力情況，依靠安全系數的選取來代替工作裝置的動態載荷、沖擊與振動分析。借鑒整體式動臂挖掘機的研究方法對輪式折疊動臂液壓挖掘機的工作裝置進行前動臂、后動臂、斗桿、鏟斗四構件聯動的方式來分析其運動特性，在理論建模和仿真分析上都較整體式動臂的三構件聯動的分析更為復雜。對折疊式動臂工作裝置進行簡化處理后建模，再對其進行仿真分析，以期得到更加接近實際挖掘作業工況下的動態特性仿真。

1 折疊式動臂工作裝置運動學模型

基于多體動力學建模方法—拉格朗日方程對折疊式動臂工作裝置進行動力學建模，模型的建立基于上文得到的D-H變換矩陣。該模型有空間轉換矩陣推導出，最終得到的是封閉式力矩函數表達式。以后動臂與機架的鏈接鉸點建立系統基坐標系，考慮到折疊式動臂工作裝置的結構特征，將前動臂和后動臂簡化為一體，得出三個自由度的折疊式動臂工作裝置動力學方程如下。

推導出折疊式動臂工作裝置基于功能平衡的拉格朗日動力學方程一般形式如下：

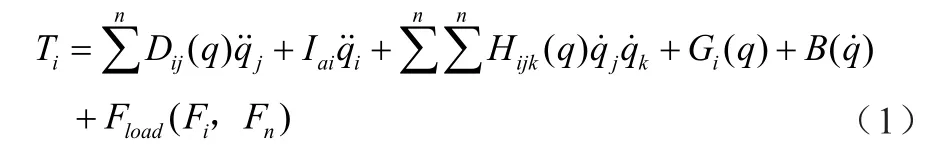
式中：Dij為折疊式動臂工作裝置各構件的等效轉動慣量（i=j）或各構件間的耦合慣量（i≠j）；Iai為傳動裝置的等效轉動慣量；Gi為折疊式動臂工作裝置各構件的重力項；Hijk為折疊式動臂工作裝置各構件兩兩鏈接關節間的向心力或各構件對于系統的哥式力作用項；B（）為折疊式動臂工作裝置各關節摩擦力矩；Fload（Fi，Fn）為折疊式動臂工作裝置的挖掘負載；n=3，是由折疊式動臂工作裝置多體系統的自由度決定。

折疊式動臂工作裝置的各構件的慣量和重力是其本身所固有的物理常量，也是影響多體系統各構件間傳動穩定性和系統內部位置參數精度的決定性因素。而多體系統內各構件兩兩鏈接關節間的向心力或各構件對于系統的哥式力作用項是在多體系統進行高速運動時產生的，對方程的影響僅限于高速運動，且速度越大影響越大。工作裝置的油缸等傳動裝置的轉動慣量可簡化到構件的慣量項中，各關節間摩擦力矩B的對折疊式動臂工作裝置多體系統的關節力矩的影響不大，因此可在計算時對其進行忽略。具體各計算項的表述如下：

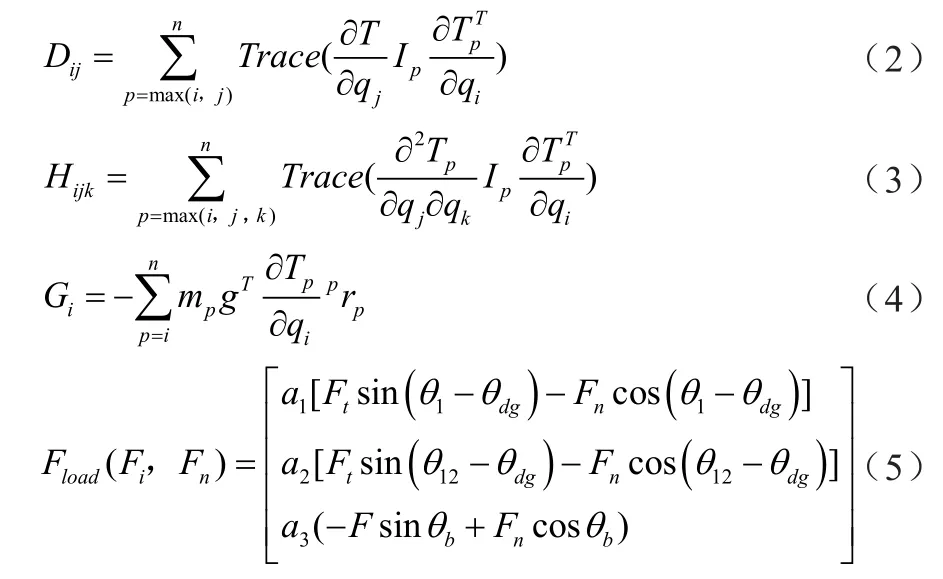
式中：Ip為構件p的偽慣量矩陣；g為重力加速度向量，由于在折疊式動臂工作裝置系統基坐標系中重力方向設置為-y，所以g =[0，-g，0，0]；prp為構件p的質心在構件p上建立的坐標系中的坐標參數；符號Trace表示矩陣的跡，即矩陣對角元素之和；由于本系統中，兩兩相連的構件組成的三個關節變量都是旋轉關節，因此，關節變量參數qi即為關節轉角參數θi。

2 剛柔耦合運動仿真

在以往的折疊式液壓挖掘機的研究中通常將工作裝置視為剛體系統進行分析研究。但是在實際工況下，折疊動臂工作裝置是一個多柔性體系統。如果不考慮柔性體對整個工作裝置的影響，進行折疊動臂工作裝置系統的動力學分析，往往不能精確地反映出實際工況下的系統運動情況和系統控制。同時對于折疊動臂工作裝置的各個構件的運動、受力情況、內部應力變化也難以反映出實際工況下的精度。因此，要準確分析得出運動中折疊動臂工作裝置的應力應變情況，就不能將工作裝置當作剛性系統來處理。但是如果完全將工作裝置當作柔性體處理，將會使設計計算的成本過高，反而不利于現實生產情況。考慮到折疊動臂工作裝置的斗桿受外部載荷的影響最為突出，且剛度相對較小，在實際生產中往往以疲勞斷裂為主。將斗桿作為柔性體，前后動臂和鏟斗作為剛體來建立剛柔耦合模型。柔性體與仿真分析流程如圖1所示。

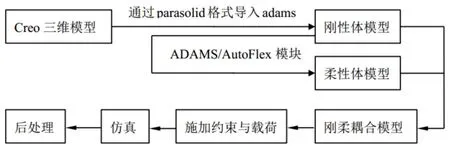
圖1 剛柔耦合模型建立流程圖

文章構建折疊動臂工作裝置的剛柔耦合模型進行仿真后，運用Durability基礎模塊的HotspotsTable得到斗桿柔性體的最大受力節點的編號、相對于原始坐標的空間位置、最大應力以及應力最大時的時間。斗桿柔性體的節點數據按照應力從大到小順序排列的信息表如圖2所示。

圖2 斗桿柔性體節點信息

由圖2可知，斗桿上應力最大節點為node-14299，進入Nodal Plots界面輸入斗桿應力最大的節點編號，就可以得到相應節點動態應力的輸出曲線，如圖3所示。

斗桿柔性體節點node-14299的動態應力在仿真開始時，由于受到驅動加載、重力、轉動慣量等的影響而出現劇烈波動。在1.5s時隨著挖掘阻力的增加應力隨之波動增加；在2.4s時其應力值達到最大值256MPa；在3.8s時隨著挖掘阻力的卸載應力節點node-14299一直在低應力范圍波動；在7.8s時卸載完成，有一個低應力階段的突變振動。該仿真曲線在開始階段（0～1.5s），由于驅動載荷、自重和自身慣量的加載出現了大幅值波動，此階段是系統響應階段，從1.5s挖掘阻力的加載開始都能與實際工況都能相互吻合。從上述分析可知，在0.12s和2.4s時均出現了最大應力。t=0.1210s和t=2.4035s時的斗桿柔性體應力云圖如圖4～圖5所示。

圖3 斗桿柔性體節點14299時間應力曲線

圖4 t=2.4035s時斗桿柔性體應力云圖

圖5 t=0.1210s時斗桿柔性體應力云圖

從最大卸載高度、挖掘深度工況仿真結果可以得出斗桿柔性體的應力變化趨勢：斗桿最大應力受載節點都位于與斗桿油缸鉸接處的耳板上，該處也是工作裝置在現實作業中容易出現疲勞損傷的位置。通常對該耳板需要進行結構強化，加大耳板的厚度能有效降低該處的應力值；或者對耳板材料進行強化，通過噴丸、輯壓、氧化等表面強化處理，以提高材料表面的疲勞強度。

3 斗桿關鍵鉸點受力分析

對斗桿的關鍵鉸點進行受力分析是鉸點連接處的銷軸和潤滑裝置設計的重要依據，文章對折疊動臂斗桿的三個鉸點（斗桿與鏟斗、斗桿與鏟斗液壓桿、斗桿與前動臂）進行剛性體與柔性體的對比分析。仿真時間設置成11s，steps設置成2000。先后對折疊動臂工作裝置進行斗桿剛性體仿真和斗桿柔性體仿真。選取JOINT_21（斗桿與前動臂鉸點）、JOINT_25（斗桿與鏟斗油缸鉸點）、JOINT_30（斗桿與鏟斗鉸點）三個約束生成其受力曲線，如圖6～圖11所示。

圖6 斗桿剛性體與前動臂鉸點受力曲線

圖7 斗桿柔性體與前動臂鉸點受力曲線

圖8 斗桿剛性體與鏟斗油缸鉸點受力曲線

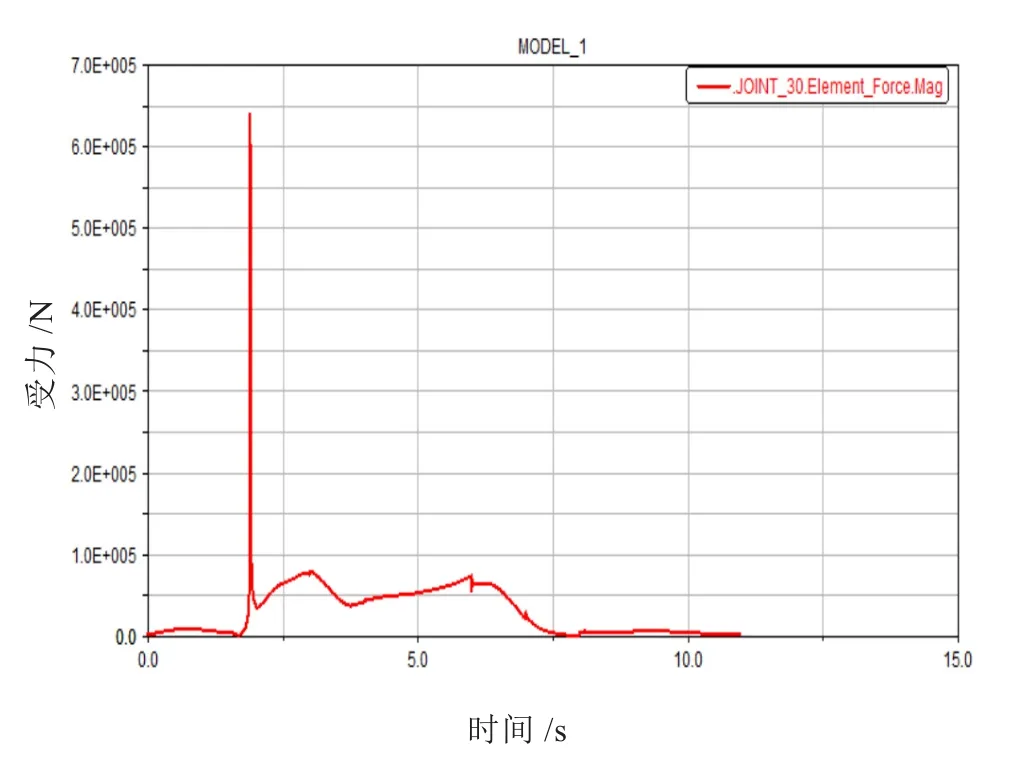
圖10 斗桿剛性體與鏟斗鉸點受力曲線

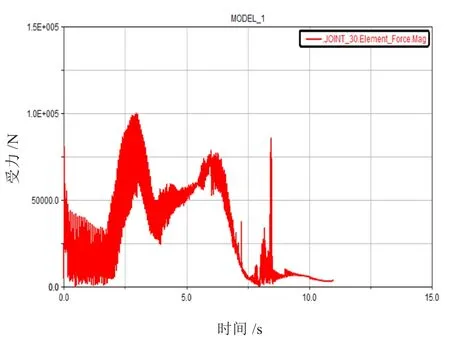
圖11 斗桿柔性體與鏟斗鉸點受力曲線

由圖6～圖11可知，斗桿剛性體和斗桿柔性體仿真得出的斗桿三個鉸點的受力曲線大致走勢基本上相同，斗桿柔性體仿真曲線可看成以斗桿剛性體仿真曲線為走勢的波動曲線；斗桿柔性體仿真得出的鉸點受力曲線值均大于剛性體仿真曲線。

在整個最大挖掘、卸載工況仿真中，在自重、慣性力和外載荷作用下，鉸點受力曲線波動的比較明顯，且在0～4s內的波動程度都比較劇烈，后續波動比較平緩。0～4s內的劇烈波動可分為2個階段：0～2s響應波動階段，仿真初始各項參數的加載和各組油缸依次開始動作時的沖擊，仿真軟件需要對其有一個響應時間，因此這一階段的仿真曲線與現實情況會有一定差異。2～4s外載荷加載波動階段，這一階段外載荷變化劇烈（挖掘阻力從零到最大值再到零，挖掘物重由零到最大值），系統對其響應波動與實際情況相符。

在斗桿與鏟斗的受力曲線圖10～11中，剛性體系統仿真曲線在1.5s時有一個受力突變階段。此時刻正好是外載荷開始加載點，剛性體系統對其響應過激，無法反映出挖掘負載逐步加載的實際情況。而柔性體曲線隨著外載荷的加載波動上升；在7.8s時刻挖掘物重完全卸載且卸載時間較短，柔性體曲線此階段波動反映出快速卸載時鉸點受力變化情況，剛性體曲線對快速卸載階段響應平緩受力曲線接近零。剛柔耦合模型較剛性體模型仿真更接近實際作業中的真實受載情況，且對外載荷的響應更加靈敏不失真。

4 結論

利用多體動力學分析軟ADAMS件對折疊動臂工作裝置進行了剛性體系統、剛柔耦合系統動態特性仿真分析。將三維模型導入ADAMS進行仿真前處理、約束設置，按照前文分析的加載挖掘負載和驅動載荷。在Auto Flex模塊中生成斗桿柔性體后進行剛柔耦合仿真。得出了斗桿在最大挖掘、卸載工況下的受力情況；分析了最大受力節點node-14299的應力變化曲線，根據此節點的應力變化曲線得出最大受力時刻t=0.1210s和t=2.4035s的斗桿柔性體應力云圖，分析得出結構受載最惡劣部位位于斗桿與斗桿油缸鉸接處的耳板上。最后分析比較了剛柔耦合系統與剛體系統的斗桿關鍵鉸點的受力變化，得出剛柔耦合系統比剛性體系統仿真數據更為接近實際工況中的作業情況。