小學數學結構化學習的優化路徑

芮金芳

摘要：小學數學結構化學習是指在大單元整合視野下，基于學生已有認知經驗建構的動態化的知識結構體系。結構化的過程也是促進學生個性化認知的過程。當前，在小學數學課堂中存在知識零散、學習淺層、思維離散等問題。教師應引導學生養成整體、系統、深度、結構化的數學學習習慣。要達成這樣的目標，需要找到結構化學習的優化路徑，包括：表征概念的核心要素，建構“塊知識”的整體結構;促進算理的深層理解，建構“類知識”的方法結構;體悟策略的思想滲透，建構“群知識”的關聯結構;著重反思的素養積淀，建構“類思想”的循環結構。

關鍵詞：結構化學習;塊知識;類知識;群知識;類思想

結構，在《現代漢語詞典》中解釋為“組成整體的各部分的搭配和序列”。皮亞杰認為，認識不僅具有結構，而且認識是一個由從低級到高級不斷建構、完善結構的過程。布魯納則認為，一個人在學習歷程中，不是簡單地把概念、信息、知識堆砌起來，各種知識之間充滿縱橫交錯的復雜聯系，是一個動態的結構。小學數學結構化學習是指在大單元整合視野下，基于學生已有認知經驗建構，生長動態化的知識結構體系，促進學生個性化認知的學習過程。在這個過程中，學生整體感悟知識結構，促進深度學習發生，積淀數學核心素養。當前，在小學數學課堂中存在知識零散、學習淺層、思維離散等問題。在教學中，教師應引導學生養成整體、系統、深度、結構化的數學學習習慣。要達成這樣的目標，需要找到小學數學結構化學習的優化路徑。

一、關聯核心要素，建構“塊知識”的整體結構

數學概念是對數量關系、空間形式特征的概括，它是同類事物本質特征聯合起來所形成的一種屬性。數學概念的形成是抽象、理性的。要讓學生理解抽象的數學概念，需要把諸多相關聯的核心要素進行一定的意義建構，從而獲得對概念本質的理解，形成良好的整體認知結構。

如在教學“認識分數”一課時，一位教師提供了不同形狀的圖形，讓學生折一折、涂一涂，表示出他們的二分之一。這位教師精選結構化的資源素材，用核心問題引領學生發現知識之間的共同要素，引導學生提煉二分之一的本質屬性。在這個過程中，學生結構化地整體理解和掌握了分數的知識。

師：如圖1，這些圖形的折法不同，涂色部分的形狀也不一樣，為什么都能表示是這張長方形紙的二分之一呢？

生：這些折法都是把一張長方形的紙平均分成兩份，涂色部分是其中的1份。所以，涂色部分都是長方形的二分之一。

師：除了這些折法，還有其他折法也能表示出這張長方形紙的二分之一嗎？

生：只要沿著長方形的中心點任意分成2份，都可以表示它的二分之一。（如圖2）

師：如圖3，這些圖形形狀各不相同，涂色部分的形狀也不一樣，為什么涂色部分也都能用二分之一表示呢？

生：不管圖形的形狀如何，只要把它平均分成2份，涂色部分是其中的1份，就可以用二分之一來表示。

學生在教師提供的豐富多樣、具有結構化資源的素材中，從兩個維度即同一組內圖形大小、形狀、顏色完全相同和不同組內大小、形狀、顏色不相同進行動作表征和圖形表征，在多次深度比較辨析中逐步剝離，去除分數次要的、非本質的特性，保留聚焦“只要平均分成2份，每份就是它的二分之一”符號表征的核心要義。在具有結構性、整體性、關聯性素材的利用和比較中，學生對“二分之一”這個分數核心概念的意義建構，逐漸從模糊走向清晰、從單一走向多維、從零散走向整體，形成了比較完備的整體認知結構，也為后續進一步學習“認識一個整體的幾分之一”“分數的意義”奠定了基礎。

二、深度理解算理，建構“類知識”的方法結構

學習是學生基于自身認知經驗基礎上的一種再認識、再提升、再生長。在整個小學階段的計算學習中，如何實現算理理解與算法建構的有機統一，一直是整數、小數、分數運算中的核心問題。學生對于算理和算法的學習，主要體現在口算、估算、筆算中。筆算的算理和口算基本一致，但算法往往需要經歷由“原始”到簡潔的規范過程，而且稍復雜的筆算算理與算法都是在簡單筆算基礎上延伸、發展而來的。

基于這樣的認識，在教學“兩位數乘兩位數筆算乘法（不進位）”時，我立足學生已有的口算經驗，通過對比和遷移，豐富了學生對筆算乘法類結構特征的整體認識和結構把握，架構起了多樣算法之間的內在意義聯結。

如學習24×12時，我利用導學單呈現了口算、點子圖、豎式計算的三種方法。

拆分法：

24×10=240;24×6=144;

24×2=48;144×2=288。

240+48=288。

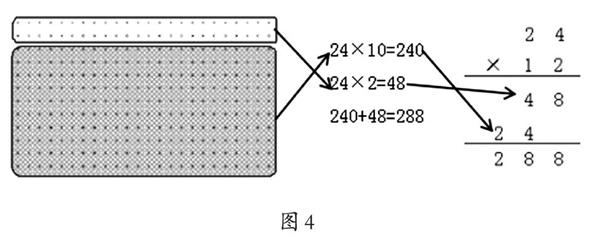
不同的算法將學生原有計算經驗中“先拆再合”的思想充分展示了出來，使學生在結構化對比、溝通中發現了這些不同算法之間的內在關聯。點子圖直觀地還原出了兩位數筆算乘法的算理意義，以形助數，幫助學生以直觀可視的方式理解了背后的算理。同時，它與口算中的“分步式”完全相同，幫助學生打通了“圖式—分步式—豎式”之間的結構通道，在整體比較中找到了各算法之間的融通點，實現了由明確算理到建構算法的自然過渡。（如圖4）

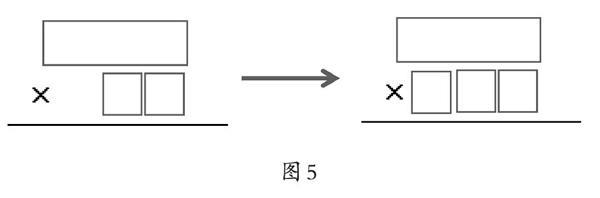
在形成兩位數筆算乘法一般計算方法后，我引導學生回顧以前學過的“兩位數乘一位數筆算乘法”，并提問：如果是三位數乘兩位數該怎樣算？任意數和兩位數相乘呢？任意數和三位數相乘呢？（如圖5）

皮亞杰曾說：“全部數學都可以按照結構的建構來考慮，而且這種建構始終是開放的……這種結構或者正在形成更強的結構，或者由更強的結構來予以結構化。”學生從乘數一位數出發，在類推聯想到兩位數、三位數、甚至更多位數的計算中，在遷移與對比中，實現了整數乘法筆算的橫向整合，形成了整數筆算乘法一般化的“算理”結構模型，構建了筆算乘法的網狀關聯結構，加深了對筆算乘法算理本質的深度理解。

三、體悟策略思想，建構“群知識”的意義結構

“解決問題的策略”這個板塊的內容是從三年級開始每冊安排的策略主題學習。具體內容分布如表1。

教材一共編排了8次“解決問題的策略”專題學習，雖然策略學習內容不同，但教材在策略教學的體系編排結構、內容展開、過程推進中都具有類似的關聯度。

（一）教材編排結構上的關聯性

不管是哪一種策略教學，教材都按照解決問題的四大板塊展開，即“理解題意—分析關系—自主解答—回顧反思”，引導學生經歷分析和思考問題的全過程。正如波利亞在《怎樣解題》一書中提到，解題過程一般包括四個步驟：弄清問題、擬定計劃、實施計劃、回顧反思。

（二）學習內容展開上的關聯性

以五年級上冊“一一列舉的策略”為例。首先，以“王大伯圍柵欄”典型實際問題情境切入，激發學生了解這個策略是什么策略、它有什么作用、具體該怎樣實施的學習內需;其次，結合具體數量關系的分析思考，逐步內化“一一列舉”策略，初步感悟在解決什么問題時可以運用這一策略;最后，隨著策略運用解決問題中經驗的逐步累積，學生自覺形成靈活選擇策略解決問題的意識，并能學會自我監控回望策略運用的全過程。這樣的策略學習內容展開邏輯，同樣適用于其他策略的學習。

（三）策略推進過程中的關聯性

學生解決問題策略的形成不是一蹴而就的，它是一個潛移默化、循序漸進的過程。所以，不管哪種策略的學習，都需要貫穿“策略需要—策略感知—策略體驗—策略形成—策略應用”這一學習線索，在策略學習中，學生只有將自身的學習經歷提煉上升為策略經驗，方能充分體驗與深刻理解不同策略的本質要義。

布魯納認為，掌握事物的結構，就是以使許多別的東西與它有意義地聯系起來的方式去理解它。學習結構就是了解他們之間是怎樣相互關聯的。在解決問題策略學習中我發現，任何一種策略學習都不是孤零零的一個節點，如果利用關聯整合視角發現策略教學中的聯系，就能組建一個更大的策略群學習結構網絡，由點及面、由淺入深地建立策略學習的生長序列，架構不同策略之間的意義聯結，促進策略學習中知識、經驗、思想的深度融合。

四、積淀反思素養，建構“類思想”的循環結構

結構化學習，不僅要引導學生感悟數學知識之間的顯性結構，更要領悟方法形成中的隱形思維結構，生長出結構化學習過程中的關聯性思維、整體性思維、系統性思維、邏輯性思維，并拓展應用到新的數學學習中。這樣，才能引導學生逐步形成數學核心素養。

美國心理學家波斯納認為，沒有反思的經驗是狹隘的經驗，最多只能是膚淺的知識。結構化學習給學生提供了整體建構、尋求關聯、邏輯判斷、主動創造的學習歷程和思維進階空間，在反思中有助于深化學生對數學知識和數學思維方式的再認識、再思考、再理解、再創造。同時，有助于促進學生思維整體結構的深層次運行，促進學生元認知能力的發展和提升。

在學生學習了“解決問題的策略（畫圖）”后，教師要引領學生回望審視解決問題的全過程，思考：這個解決問題的策略是什么？這個策略是怎樣解決這一類和差實際問題的？我們是怎樣想到畫圖的？為什么選擇畫線段圖？畫圖時我們要注意什么？畫圖對我們進一步理解、分析、思考解決問題有什么好處？同時，要回顧“在以前的學習中，有哪些地方運用畫圖策略來解決問題的？”還可以延伸至“數學中的畫圖策略除了今天學習的畫線段圖還有其他的嗎？”“除了畫圖策略還有其他解決問題的策略嗎？”“今天研究的數學上的畫圖策略與美術課中畫圖有什么異同點？”這樣瞻前顧后地追問，將學生原先積累的運用畫圖策略分析、思考、解決問題的零散經驗匯總聚合，有助于學生從以往的學習經歷中剝離、提煉出數學思想方法和應用策略，形成具有遷移作用的策略體驗。同時，能將這種體驗延伸至后續的其他解決問題的策略學習中，將學生的認知方法、結構不斷豐富、完善、打開，形成一個開放、循環、流動的結構，真正觸發學生思維的深度生長。

結構化學習，需要教師在教學中形成結構性思維，以整體關聯的視角、開放動態的內容、連續循環的過程、遷移生長的反思，不斷促進學生結構化學習的自然發生，并在知識的理解、整合、關聯、遷移中培養學生的結構化思維，以真正促進高階思維的形成，實現優質化的深度學習。

參考文獻：

[1]張興華.兒童學習心理與小學數學教學[M].南京：江蘇教育出版社，2011.

[2]劉月霞，郭華.深度學習：走向核心素養[M].北京：教育科學出版社，2019.

[3]郭元祥.知識的性質、結構與深度教學[J].課程·教材·教法，2009（11）.

[4]袁國超.基于核心素養的深度學習實現路徑[J].江蘇教育研究，2019（11）.

（責任編輯：楊強）