非對稱耦合雙振子的二維復(fù)雜運(yùn)動

徐利利

（銀川職業(yè)技術(shù)學(xué)院 寧夏·銀川 750000）

0 緒論

耦合振子研究概述。非線性問題是當(dāng)前物理研究的熱門問題，但其求解具有極大難度，除了少部分特殊情況可以用解析法解決以外，大部分問題要依靠數(shù)值方法，利用計(jì)算機(jī)為工具，才能得出其結(jié)果。耦合振子大量的存在于物理、化學(xué)、生物等學(xué)科中，這對科學(xué)的發(fā)展有著很大的推動作用。要弄懂耦合振子是怎樣工作的，首先必須搞清單個(gè)振子是怎樣工作的。單個(gè)振子是指發(fā)生周期行為的系統(tǒng)，而耦合振子的行為則很復(fù)雜。如兩個(gè)相同振子耦合時(shí)，有兩種可能：同步，即相位差為零；和反同步(或稱為異步)即相位差為半個(gè)周期。而對于多個(gè)耦合振子，它們的行為則更為復(fù)雜。目前數(shù)學(xué)上仍無法弄清它們運(yùn)動的機(jī)理。然而，不管哪種情形，同步現(xiàn)象是耦合振子中可能出現(xiàn)的一種基本行為，并且每個(gè)振子的振動都要影響它同其他振子的相互作用，于是它們形成了一個(gè)耦合振子系統(tǒng)。所以，研究耦合振子系統(tǒng)的運(yùn)動是有著重要的現(xiàn)實(shí)意義的。

本文建議一個(gè)非對稱彈簧雙振子模型，通過拉格朗日函數(shù)獲得其運(yùn)動方程，數(shù)值求解方程獲得振子的運(yùn)動軌線。結(jié)果表明振子的運(yùn)動強(qiáng)烈依賴于初值，表現(xiàn)在振子運(yùn)動軌線因初值不同而不同，且在相空間中做遍歷運(yùn)動。這是因?yàn)槲覀兯疾斓恼褡酉到y(tǒng)無耗散因素存在，因而是保守系統(tǒng)中典型的非線性動力學(xué)行為。我們得到的這個(gè)結(jié)果將提醒相關(guān)研究者，當(dāng)不存在耗散因素時(shí)耦合振子系統(tǒng)是一個(gè)保守的非線性動力學(xué)系統(tǒng)，這樣的系統(tǒng)有其固有的動力學(xué)特征，另外，一些看似周期的運(yùn)動實(shí)際可能是遍歷運(yùn)動，而遍歷運(yùn)動往往是混沌或準(zhǔn)周期的，而這種運(yùn)動單憑肉眼觀察振動曲線是無法與周期運(yùn)動相區(qū)別的。

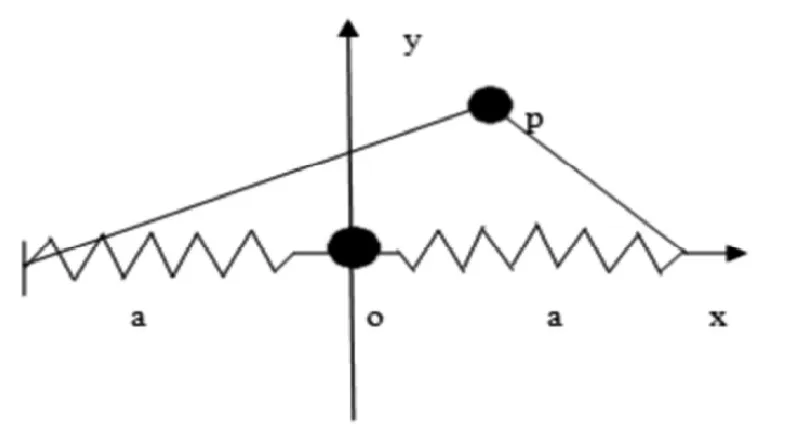
圖2-1 雙彈性振子模型

1 非對稱耦合雙振子模型

1.1 彈簧振子模型的建立及系統(tǒng)的運(yùn)動方程

非對稱雙彈性振子物理模型可以用一個(gè)在光滑水平面上運(yùn)動的質(zhì)量為m的質(zhì)點(diǎn)來描述，它與兩個(gè)彈性系數(shù)分別為k1和k2，原長為a的彈簧相連。這里，光滑意味著忽略能量耗散，是一個(gè)理想體系。平衡時(shí)這兩個(gè)彈簧成一條直線，此時(shí)彈簧原長為a，質(zhì)點(diǎn)在水平的xoy平面內(nèi)作微小振動。為簡單起見，質(zhì)點(diǎn)平衡位置取在原點(diǎn)o處。模型由圖1表示

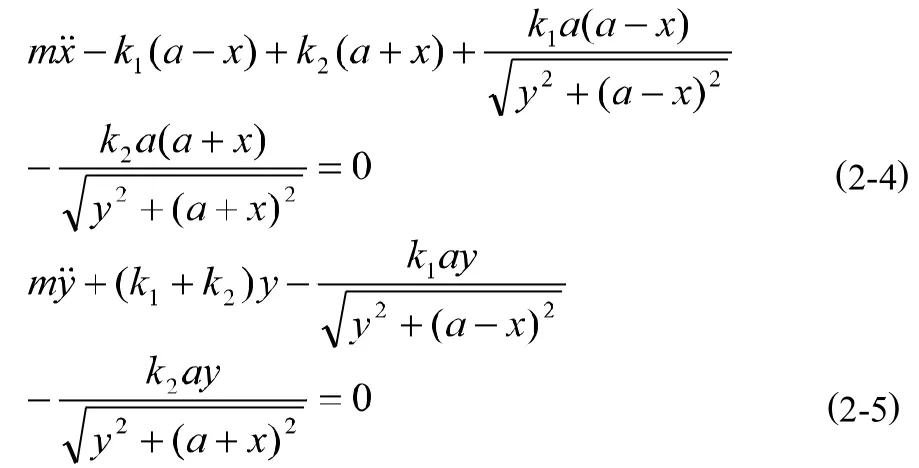
顯然，方程(2-4)和(2-5)是一組非線性耦合方程。表明線性彈性振子通過相互耦合將轉(zhuǎn)變?yōu)榉蔷€性振動，這樣的非線性方程組很難直接解析求解，我們將借助于軟件Mathematica數(shù)值求解。

2 Lyapunov指數(shù)與混沌運(yùn)動

2.1 Lyapunov指數(shù)與混沌運(yùn)動

為了便于計(jì)算 Lyapunov指數(shù)以確定耦合振子的運(yùn)動性態(tài)，我們將通過升維降階的辦法將方程組(2-4)和(2-5)化為一階方程組如下：

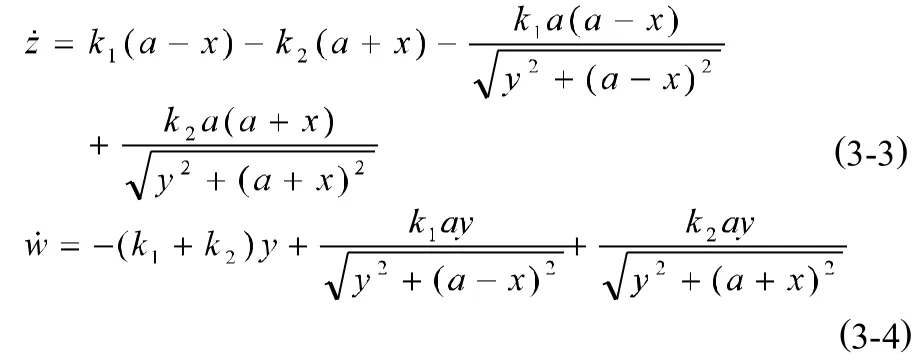
這里彈性振子質(zhì)量m=1kg，彈簧原長a=1.0m，設(shè)彈性系數(shù)為控制參量。根據(jù)Lyapunov指數(shù)譜。譜線顯示參數(shù)范圍，絕大多數(shù)參數(shù)區(qū)至少有一個(gè)指數(shù)大于零，表明振子的運(yùn)動是混沌的；而在參數(shù)范圍，四個(gè)指數(shù)值在零附近振蕩，表明振子的運(yùn)動是準(zhǔn)周期的或在個(gè)別小參數(shù)區(qū)域是周期的。

2.2 模擬不同初態(tài)下振子的混沌軌線

作為一個(gè)例子，挑選混沌區(qū)的一個(gè)參數(shù)，取初始條件將對應(yīng)振子的軌線一一模擬出來。假定彈性振子質(zhì)量m=1 kg，彈簧原長a=1.0 m，彈性系數(shù)分別為k1=0.06 N/m和k2=0.07 N/m。現(xiàn)用數(shù)值方法研究系統(tǒng)在給定的不同初始條件下軌跡的響應(yīng)。當(dāng)初始條件分別為；利用Matlab語言的超強(qiáng)數(shù)值計(jì)算功能，求解方程(2-4)和(2-5)，得到x、y方向振動曲線。可以得出沒有耗散性的系統(tǒng)就沒有吸引性，因此振子的軌線均因初態(tài)不同而不同，可以說是：“一點(diǎn)一線”，明確了混沌和準(zhǔn)周期參數(shù)區(qū)之后，我們有必要將模型還原為方程組(2-4)和(2-5)。則方程組(3-1)-(3-4)的解在y-x平面的投影確信無疑就是原方程組的解。其結(jié)果顯示了運(yùn)動軌線對初始條件的強(qiáng)烈依賴。

3 準(zhǔn)周期運(yùn)動

3.1 不同初態(tài)下振子的準(zhǔn)周期軌線

非線性保守系統(tǒng)“一點(diǎn)一線”的運(yùn)動特征對準(zhǔn)周期運(yùn)動也不例外，下圖中給出了準(zhǔn)周期參數(shù)中k1=0.1 N/m，k2=0.09 N/m時(shí)兩組不同初始條件下振子的準(zhǔn)周期運(yùn)動軌線。初值為。利用Matlab語言的超強(qiáng)數(shù)值計(jì)算功能，求解方程(2-4)和(2-5)，得到x、y方向的振動曲線。在微小振動的條件下，非對稱耦合振子的振動是非簡諧的周期性振動，在保守力系統(tǒng)中，非線性振動系統(tǒng)的振幅、周期或頻率與初始位置和初始速度有關(guān)系，分析發(fā)現(xiàn)在x方向和y方向系統(tǒng)的振動周期與振幅成反比，x方向和y方向系統(tǒng)的振動周期與初始位置有關(guān)，初始位置增大，振動周期變小；x方向和y方向系統(tǒng)的振幅與初始位置和初始速度有關(guān)，初始位置增大，振幅增大；初始位置不變，若初始速度增大，則振幅也增大。結(jié)果表明振子的準(zhǔn)周期運(yùn)動同混沌運(yùn)動一樣是遍歷運(yùn)動，而且運(yùn)動軌線與初態(tài)一一對應(yīng)。但是，單從振子的運(yùn)動軌線看，無法區(qū)分混沌運(yùn)動與準(zhǔn)周期運(yùn)動。唯一可靠的辦法是計(jì)算系統(tǒng)的Lyapunov指數(shù)。

4 結(jié)束語

非對稱彈簧系統(tǒng)中常見的二維非線性振動問題，可利用拉格朗日方法得到其振動控制微分方程，借助于計(jì)算機(jī)和Matlab語言在計(jì)算方面的超強(qiáng)功能，成功解決了該類非線性振動問題。這種方法有效簡便，為非線性問題探索出了一種較好的求解途徑。模擬研究了非對稱耦合雙振子系統(tǒng)的平面運(yùn)動，由 Lyapunov指數(shù)判斷這個(gè)系統(tǒng)既有混沌運(yùn)動又有準(zhǔn)周期運(yùn)動，當(dāng)然不排斥一些參數(shù)區(qū)存在周期運(yùn)動。由于我們所考察的系統(tǒng)是一個(gè)典型的保守非線性系統(tǒng)，所以即使準(zhǔn)周期運(yùn)動，其運(yùn)動軌線強(qiáng)烈依賴于初始條件，周期運(yùn)動情形與此類似。因此，這樣的系統(tǒng)能夠展示非常豐富且復(fù)雜的運(yùn)動形態(tài)。