星載自動識別系統信號的多普勒頻移估計
張家旭,李 波,崔 文
(西安郵電大學 通信與信息工程學院,西安 710000)
0 引 言
自動識別系統(Automatic Identification System,AIS)是一種用于海上船舶通信的廣播式自動報告系統。其作為一種近距離船岸通信應用,已為許多國家及地區實現了海上監控。但現今的海上船舶需要的不僅僅是提供位置、標識和速度之類的信息,越來越多的危險或非法貨物需要通過檢測和跟蹤船舶來提高安全性。在AIS通信時,由于船舶數量龐大導致的時隙沖突和有限的覆蓋范圍正變得越來越嚴重,且AIS成熟技術進入到中國還出現了靈敏度和穩定性不高的情況。為了克服這些問題,人們提出了一種采用頻譜感知和正交頻分復用(Orthogonal Frequency Division Multiplexing,OFDM)等技術[1-5]的認知AIS,其雖然提高了海上交通效率,但仍未解決無線電覆蓋的嚴重缺陷,且其服務范圍僅在40海里內。
因此,近年來一種基于衛星的AIS被提出,該系統可以服務于海上交通觀測和非法運輸監測等,衛星通信具有寬帶傳輸能力、大覆蓋范圍和全球導航衛星系統等優點。雖然基于衛星的AIS可以建立衛星—船舶的通道,但會遇到衛星相對移動的多普勒頻率偏移等挑戰[6]。由于傳輸過程中環境較復雜,信號衰減較大,使接收到的信號信噪比(Signal-to-Noise Ratio, SNR)較低,因此AIS接收機在進行信號解調及解碼前必須進行多普勒頻譜估計及校正。為了解決上述問題,本文提出了一種適用于衛星與船舶之間AIS的多普勒頻移估計算法。
1 AIS信道模型分析
衛星能夠為所有配備AIS設備的船舶建立通信聯系。采用基于衛星的AIS基站,可覆蓋幾乎所有可航行海洋地區的沿海基站來擴展AIS的通信距離,如圖1所示。
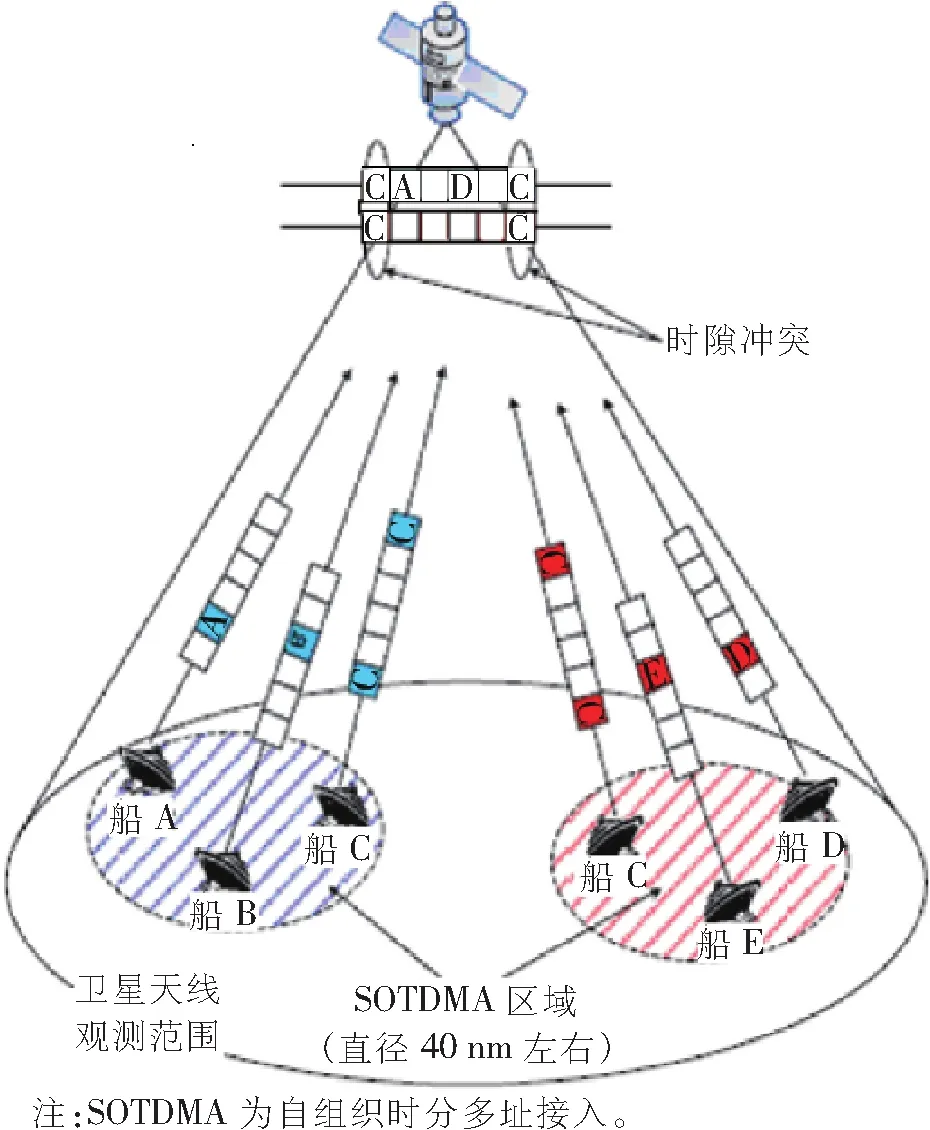
圖1 衛星AIS基站示例
衛星軌道高度一般為600~1 000 km,運行速度為7.5 km/s,所以AIS信號的多普勒頻移最大為±4 kHz,再加上相對運動引起的多普勒頻移,因此必須進行多普勒頻譜校正。為了解決這個問題,研究人員提出了一些方法[7-9],但這些方法都只考慮了加性高斯白噪聲(Additive White Gaussian Noise,AWGN)。而AIS信號的誤碼率是由于海洋表面的信號反射引起的多徑衰落和加性非高斯噪聲[9]所引起的,若多徑信號來自海面上多個統計獨立點的反射,則可以建模為統計獨立高斯信號的隨機過程。由于多徑信號的最大時差明顯小于帶寬倒數,所以系統中采用時變非頻率選擇性衰落信道。此外,由文獻[10]可知,對于通信信道帶寬為25~50 kHz的海上衛星通信,其信道可以被認為是非頻率選擇性衰落。因此,25 kHz信道帶寬的AIS無線信道可以看作是一個非頻率選擇性的萊斯衰落過程。
一般情況下,加性噪聲被假定為高斯分布,這是因為其數學可處理性。然而,由實驗測量可知,海面環境中的加性噪聲是非高斯噪聲[11]。非高斯噪聲有很多形式,本文選用高斯混合模型(Gaussian Mixture Model,GMM)[12]對加性噪聲進行建模。
2 AIS多普勒頻移信道分析
本節首先描述發送信號模型,然后給出信號模型的一些背景材料,包括高斯最小頻移鍵控(Gaussian Minimum Shift Keying,GMSK)調制信號、衰落信道和GMM[13]。
AIS發送信號模型如圖2所示。定義x(t)為AIS的時域信號;y(t)為GMSK調制后的時域信號;非頻率選擇性萊斯衰落信道系數為h(t);非高斯噪聲為g(t)。

圖2 AIS發送信號模型
通過高斯低通濾波器和最小頻移鍵控(Minimum Shift Keying,MSK)調制器得到GMSK調制信號。GMSK信號模型如圖3所示。

圖3 GMSK信號模型
非頻率選擇性萊斯衰落信道系數h(t)已在其他文獻中進行了仿真和建模,在文獻[14-15]中,h(t)=KhLOS(t)+KhNLOS(t),式中:K 為萊斯因子;hNLOS(t)為非頻率選擇性萊斯非視距衰落分量,其均值和自相關函數分別為零和零階貝塞爾函數,其實部和虛部為獨立的高斯隨機變量;hLOS(t)為非頻率選擇性萊斯視距衰落分量,文獻[14]給出hLOS(t)=exp(j2πfdtcosθ0+jφ0),式中,j為虛數,其視距分量fd、θ0和φ0分別為最大多普勒頻移、到達角和初始相位。
由此,非高斯噪聲可由多個高斯分量的加權和GMM產生,并假定非高斯噪聲為零均值[16-17]。
3 AIS多普勒頻移估計算法
在上述背景下,可以注意到估計的多普勒頻移隱藏在非頻率選擇性萊斯衰落信道中,多普勒頻移并不容易被提取出來。為了檢驗多普勒頻移估計算法,我們將模擬信號進行抽樣判決轉化為數字信號,對應的GMSK調制后的時域信號y(t)定義為離散信號y(n),定義AIS數據的時域信號x(t)為離散信號x(n)、定義非頻率選擇性萊斯衰落信道系數h(t)為離散函數h(n)、定義非高斯噪聲g(t)為離散函數g(n)。分別模擬函數y(n)的實部Re(y(n))與虛部Im(y(n)),幅值如圖4所示。
圖4 y(n)實部與虛部簡單模擬
由上述特征可知,若不考慮非高斯噪聲信號,則忽略萊斯因子K及hLOS(t)分量的初始相位和hNLOS(t)分量。輔助參數估計利用訓練序列替代GMSK調制信號。定義替代后的信號模型為p(n)=y′(n)·x*(n),式中:y′(n)=x(n)·h(n);x*(n)為x(n)的共軛。
設調制度BTb=0.4,訓練序列ai=(-1 -1 1 1 -1 -1 1 1 -1 -1 1 1 -1 -1 1 1 -1 -1 1 1 -1 -1 1 1)。如圖5所示,恢復估計的多普勒頻移的p(n)與y(n)相比完全一致。分別模擬p(n)與y(n)。
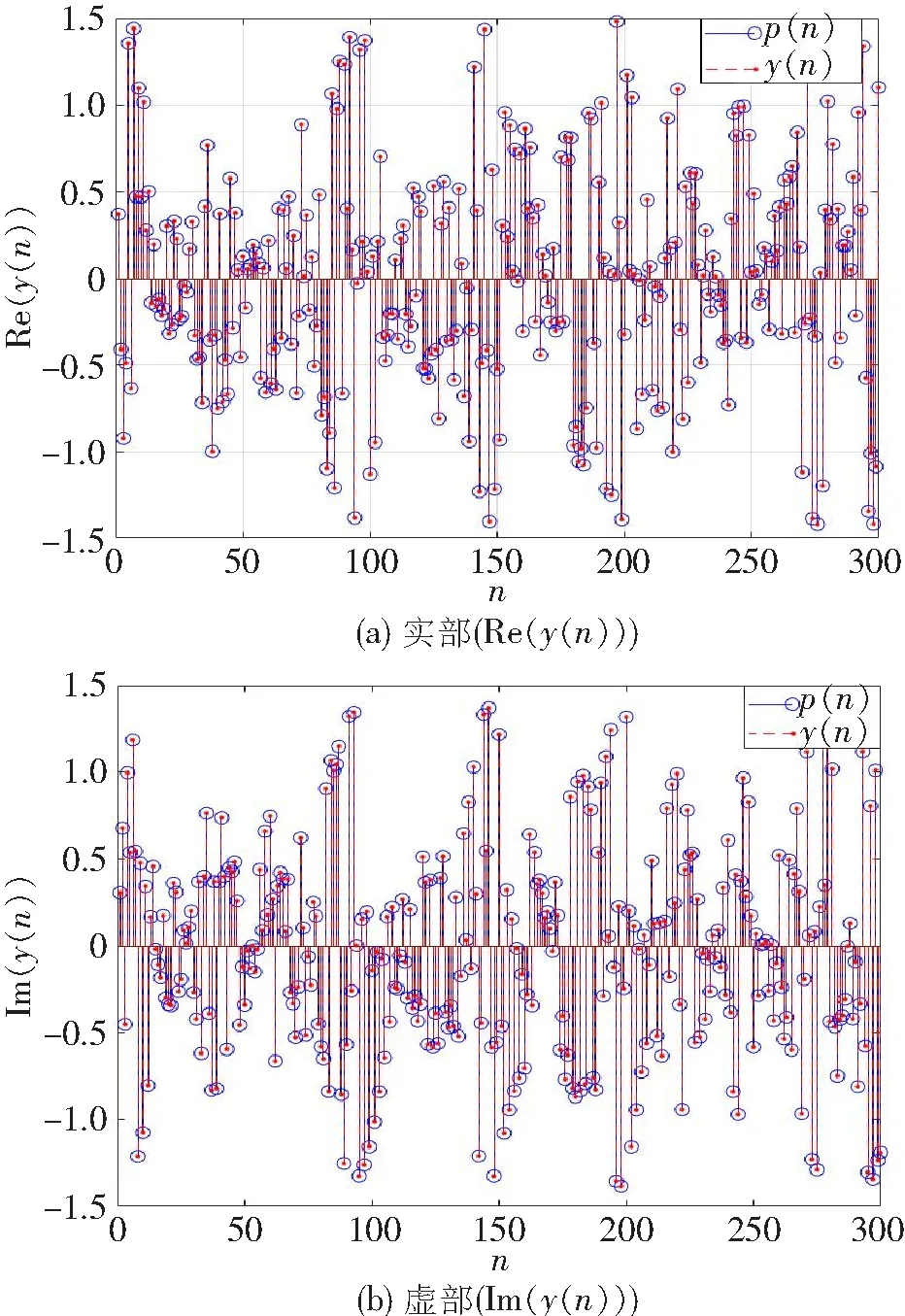
圖5 p(n)與y(n)實部與虛部簡單對比
由先前討論可知,除了非高斯噪聲和GMSK調制信號的參數干擾外,很難直接提取多普勒頻移。可通過忽略GMSK調制用訓練序列代替,來完成計算。根據前面的討論,將接收到的信號y(n)與x*(n)相乘,即
式中,v(n)為具有零均值的非高斯噪聲。由式(1)可知,已取消對信號進行GMSK調制,但對包絡估計的多普勒頻移h(n)的提取需要消除非高斯噪聲。非高斯噪聲的均值為0,為了消除非高斯噪聲的影響,對式(1)進行二階矩運算:
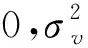
為了將多普勒頻移單獨分離出來,應消除萊斯因子K和函數J0,因此對式(2)進行四階求導,得到:
式中:l、m和q均為四階導的變量;Rzzzz(l,m,q)為z(n)的四階導運算。
為了消除K和J0,將Rzzzz(l,m,q)化簡,設定m=0、l=0、q=0,得到Rzzzz(0,0,0),化簡可得:
由式(4)可知,K是可以求解的。在下文中,我們同時消除了式(3)中的J0,設定m≠0,將l=0和q=0代入式(4)可得:
通過簡單的代數運算得到多普勒頻移的估計式:
式中,arg{·}為相位提取。上述方程給定為當前值m的多普勒頻移Δfd的估計。
4 仿真與結果
假設信號為衛星發送到船只的AIS信號,對非頻率選擇性萊斯衰落信道和非高斯噪聲進行模擬分析。通過Matlab軟件的萊斯衰落函數產生非頻率選擇性萊斯衰落信道[15],用不同參數的GMM產生具有μ=0的非高斯噪聲。通過對5 000個蒙特卡羅試驗進行平均來獲得仿真結果,并且本節中各圖均在此條件下仿真得出。載波頻率、BTb和碼元長度L分別設置為162.025 MHz、0.4和3。其中,仿真平臺選用中央處理器(Central Processing Unit,CPU)為Inter Core i5-7100、主頻為3.9 GHz和內存為8 GB的電腦,仿真軟件采用 Matlab2018a軟件,仿真條件均參考ITU-RM.1371-4建議書設置,碼元序列長度選用一個標準時隙的長度。在估計過程中采用訓練序列,假定多普勒頻移在一個突發持續時間內為恒定值,分別為:5、4和3 kHz。
在仿真中,選擇估計的多普勒頻移的均方誤差(Mean-Square Error, MSE)作為性能指標,通過對比SNR及萊斯因子K的變化來驗證本文所提算法。此外,仿真一種基于萊斯衰落信道的原方法[14]與本文所提方案進行比較。
驗證SNR時,K設為10,SNR設為5~50 dB,仿真結果如圖6所示。通過對比文獻的算法與本文所提算法可知,在不同SNR情況下,MSE分別為45和15。可見,本文算法對降低均方誤差有較明顯的作用,可以更好地估計多普勒頻移,并且參數在一定范圍內具有魯棒性。
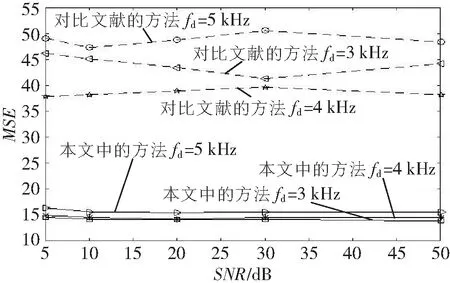
圖6 兩種算法在不同SNR下的MSE比較
驗證萊斯因子K時,SNR設置為20 dB,K設置為5~50。隨著K的增大,MSE的變化趨勢如圖7所示。在不同K值下,MSE分別下降至15和10,本文所提算法比原算法[14]的MSE更低,信號受K的波動影響小,系統精確度更高。實驗結果證明,K對衰落信道的視距分量影響較小。換句話說,K對信道性能的影響占主導地位。本系統在K值小的情況下,性能優于基于文獻[14]的算法,并且本系統可以通過改變K值來進行改進。
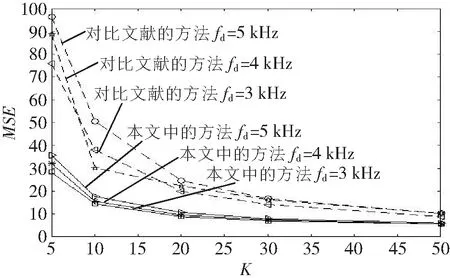
圖7 兩種算法在不同萊斯因子K下的MSE比較
由以上兩個實驗可知,本文所提算法的多普勒頻移估計性能要優于原算法,與理論仿真基本一致,具有較高的估計性能。但由于實驗環境較理想,未考慮時延影響,所以改進算法在真實環境中的性能還有待進一步研究。
5 結束語
本文研究了從衛星發送到船只的AIS信號的多普勒參數估計問題,并提出了一種新的多普勒頻移算法。對基于衛星的非頻率選擇性萊斯衰落信道和非高斯噪聲對接收到的基于衛星的AIS信號進行了估計和研究。其思想為:采用二階矩陣和四階矩陣來消除一些冗余信號及參數,并推導出了用于多普勒頻移估計的有用表達式。通過計算機仿真驗證了該方法的有效性,仿真結果表明,該方法對估計頻率范圍內的頻率具有較強的魯棒性,且此方法還可隨萊斯系數的增加提供良好的穩定性,這也證明了此方法能夠提高系統精確度。本文所提算法不僅在理論仿真上具有較好的效果,對實際信號的估計也能達到較高的估計精度,并且算法簡單、易于實現,用于AIS信號是完全可行的。

