捷聯(lián)慣導(dǎo)系統(tǒng)晃動(dòng)基座高精度快速自對(duì)準(zhǔn)技術(shù)研究
羋小龍,桂士宏,尹洪亮
(1. 海軍裝備部,北京 100071;2. 中國(guó)船舶集團(tuán)有限公司,北京 100097;3. 中國(guó)艦船研究院,北京 100192)
0 引 言
捷聯(lián)慣導(dǎo)系統(tǒng)靜基座自主對(duì)準(zhǔn)有外部信息依賴度低的特點(diǎn),可直接利用慣導(dǎo)系統(tǒng)陀螺、加表輸出和零速校正條件,完成粗對(duì)準(zhǔn)和精對(duì)準(zhǔn)[1]。傳統(tǒng)自對(duì)準(zhǔn)算法一般依靠重力矢量及地球速率矢量直接估算導(dǎo)航坐標(biāo)系到機(jī)體坐標(biāo)系的姿態(tài)變換矩陣,這種方法對(duì)對(duì)準(zhǔn)環(huán)境有嚴(yán)格的要求,一般只用于載體處于靜止或微幅晃動(dòng)條件下。對(duì)于系泊或漂浮狀態(tài)的艦艇,由于受海浪影響,造成其裝備的慣導(dǎo)系統(tǒng)測(cè)量結(jié)果受到嚴(yán)重干擾[2]。在這種環(huán)境下,直接采用地球自轉(zhuǎn)角速度作為參考信息計(jì)算初始姿態(tài)陣的方法已不再適用。但對(duì)于加速度計(jì)測(cè)量到的重力加速度信息,由于其干擾信息一般為諧波形式而且幅值小于重力加速度幅值,因此通過平滑處理可以消除,并提取出重力加速度信息,故地球重力加速度仍可直接作為粗對(duì)準(zhǔn)的參考信息[3–4]。
由于地球重力加速度在慣性坐標(biāo)系中的運(yùn)動(dòng)軌跡為一圓錐面,因此,若取在慣性坐標(biāo)系下重力加速度的投影,則其分量就能包含地球自轉(zhuǎn)角速度信息,再結(jié)合陀螺和加速度計(jì)的輸出,就可實(shí)現(xiàn)初始姿態(tài)陣的粗略估計(jì)。
1 粗對(duì)準(zhǔn)算法設(shè)計(jì)
1.1 坐標(biāo)系定義
定義如下坐標(biāo)系:
采用北天東地理坐標(biāo)系。
原點(diǎn)位于載體重心的前上右坐標(biāo)系。
1.2 算法設(shè)計(jì)
為隔離晃動(dòng)對(duì)自主對(duì)準(zhǔn)的影響,將姿態(tài)矩陣拆分為4個(gè)矩陣分別計(jì)算,設(shè)對(duì)準(zhǔn)點(diǎn)緯度為,則姿態(tài)矩陣可寫為:
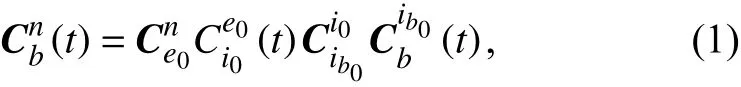
其中:
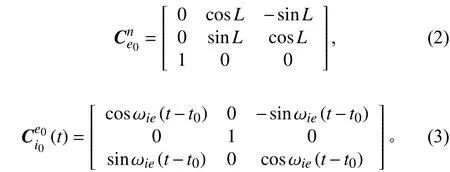


由式(7)和式(8)可得:

2 精對(duì)準(zhǔn)方案
2.1 精對(duì)準(zhǔn)方案的選擇
當(dāng)慣導(dǎo)系統(tǒng)處于大幅度晃動(dòng)條件下時(shí),其相對(duì)地球的參考速度仍可視為0,因此,選擇以速度誤差作為觀測(cè)量構(gòu)建最優(yōu)卡爾曼濾波來實(shí)現(xiàn)慣導(dǎo)系統(tǒng)的精對(duì)準(zhǔn)。
2.2 捷聯(lián)慣導(dǎo)系統(tǒng)誤差模型的建立
1)捷聯(lián)慣導(dǎo)系統(tǒng)誤差方程
考慮到慣性元件誤差以及系統(tǒng)導(dǎo)航參數(shù)誤差等的影響,構(gòu)建導(dǎo)航坐標(biāo)系為系,定義系相對(duì)系的轉(zhuǎn)角為姿態(tài)誤差角根據(jù)捷聯(lián)慣導(dǎo)力學(xué)編排方程,可獲得姿態(tài)誤差方程如下:
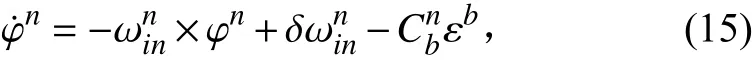
其中:
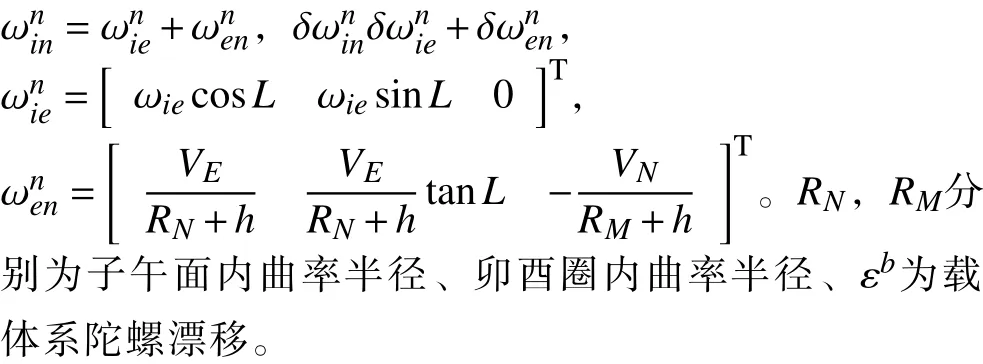
根據(jù)捷聯(lián)慣導(dǎo)速度解算方程,考慮系統(tǒng)誤差影響,獲得速度誤差方程如下:

2)捷聯(lián)慣導(dǎo)系統(tǒng)狀態(tài)空間模型
由式(14)和式(15),并設(shè)陀螺和加表的測(cè)量誤差為隨機(jī)常數(shù),可得到SISN初始對(duì)準(zhǔn)狀態(tài)方程為:

狀態(tài)變量為:
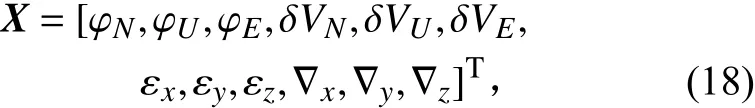
隨機(jī)噪聲狀態(tài)矢量為:

取速度誤差為觀測(cè)量構(gòu)建系統(tǒng)觀測(cè)方程:

3 試驗(yàn)驗(yàn)證與結(jié)果分析
3.1 試驗(yàn)條件
為驗(yàn)證本文提的晃動(dòng)基座自對(duì)準(zhǔn)算法,選用某中精度捷聯(lián)慣導(dǎo)系統(tǒng)為實(shí)驗(yàn)對(duì)象,分別在靜基座和晃動(dòng)基座條件下進(jìn)行自主對(duì)準(zhǔn)驗(yàn)證試驗(yàn)。當(dāng)?shù)鼐暥刃畔?9.811 75°。
3.2 試驗(yàn)過程
每組試驗(yàn)對(duì)準(zhǔn)時(shí)間為7 min,其中粗對(duì)準(zhǔn)時(shí)間120 s,精對(duì)準(zhǔn)濾波時(shí)間300 s。統(tǒng)計(jì)對(duì)準(zhǔn)結(jié)束后純慣性導(dǎo)航30 min的結(jié)果,以此來驗(yàn)證所提方法的可行性。
試驗(yàn)1:靜基座自主對(duì)準(zhǔn)驗(yàn)證試驗(yàn)。慣導(dǎo)系統(tǒng)靜止于三軸轉(zhuǎn)臺(tái)上進(jìn)行試驗(yàn)。
試驗(yàn)2:晃動(dòng)基座自主對(duì)準(zhǔn)驗(yàn)證試驗(yàn)。三軸轉(zhuǎn)臺(tái)進(jìn)行晃動(dòng),試驗(yàn)過程中慣導(dǎo)系統(tǒng)晃動(dòng)規(guī)律如圖1所示。
3.3 試驗(yàn)結(jié)果及分析
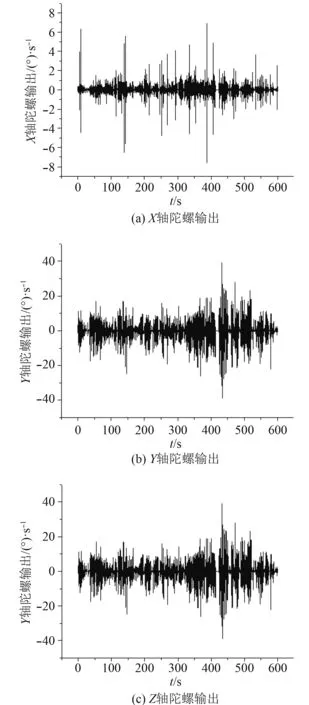
圖1 慣導(dǎo)系統(tǒng)晃動(dòng)規(guī)律Fig. 1 Inertial navigation system sloshing law
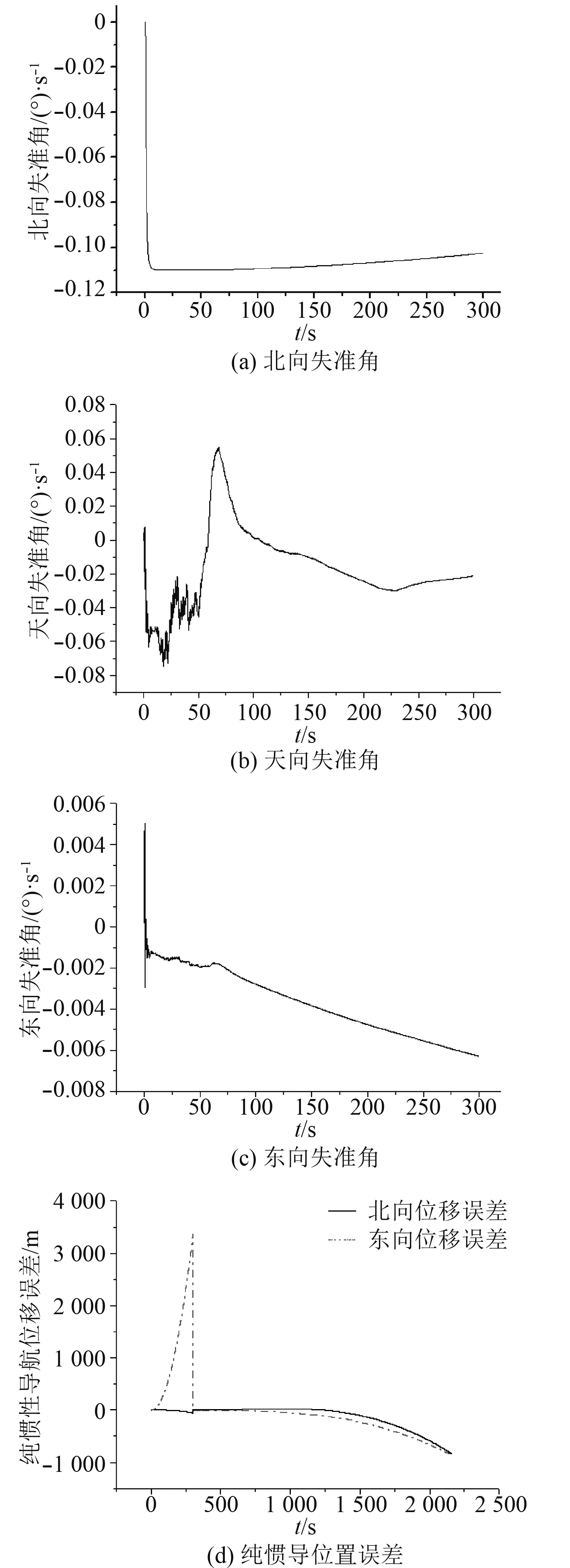
圖2 靜基座對(duì)準(zhǔn)及純慣性導(dǎo)航結(jié)果Fig. 2 Static base alignment and pure inertial navigation results

表1 不同晃動(dòng)條件下對(duì)準(zhǔn)后30 min純慣性導(dǎo)航結(jié)果Tab. 1 Results of pure inertial navigation 30 min after alignment under different sloshing conditions
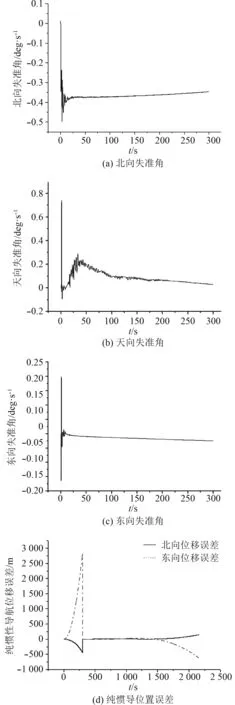
圖3 靜基座對(duì)準(zhǔn)及純慣性導(dǎo)航結(jié)果Fig. 3 Wobble base alignment and pure inertial navigation results
圖2 為靜基座對(duì)準(zhǔn)試驗(yàn)結(jié)果,圖3為晃動(dòng)基座對(duì)準(zhǔn)試驗(yàn)結(jié)果。為比較2種情況下的對(duì)準(zhǔn)效果,選用對(duì)準(zhǔn)后自主導(dǎo)航30 min數(shù)據(jù),表1為試驗(yàn)結(jié)果統(tǒng)計(jì)。
由圖2可知,晃動(dòng)基座自主對(duì)準(zhǔn)方案對(duì)準(zhǔn)效果與傳統(tǒng)靜基座自主對(duì)準(zhǔn)方法差不多,由于可觀測(cè)性和可觀測(cè)度不高,方位失準(zhǔn)角收斂速度很慢,在5 min的濾波過程中很難收斂,因而影響對(duì)準(zhǔn)精度。
由圖3可看出,晃動(dòng)基座自主對(duì)準(zhǔn)方案在晃動(dòng)條件下,失準(zhǔn)角收斂的很理想,方位失準(zhǔn)角的收斂速度也快于靜基座,從導(dǎo)航結(jié)果可以看出晃動(dòng)條件下的對(duì)準(zhǔn)效果明顯好。
由表1統(tǒng)計(jì)的各項(xiàng)導(dǎo)航結(jié)果指標(biāo)可以看出,晃動(dòng)基座下自主對(duì)準(zhǔn)方案對(duì)準(zhǔn)精度較高。
4 結(jié) 語
本文利用慣性凝固假設(shè),建立載體慣性坐標(biāo)系,使載體坐標(biāo)系相對(duì)載體慣性坐標(biāo)系的姿態(tài)陣初值成為單位陣,從而可以進(jìn)行姿態(tài)更新解算。所提方案通過將姿態(tài)陣拆分為4個(gè)矩陣,選用重力加速度在慣性空間的投影為參考信息,消弱了晃動(dòng)的影響,保證晃動(dòng)基座下的粗對(duì)準(zhǔn)精度。利用高觀測(cè)性的卡爾曼濾波進(jìn)行狀態(tài)估計(jì),提高了算法精度。

